城市立体交通系统中污染物传播特性数值模拟

窦鸿文 ,明廷臻 *,许 杰 ,李政桐 ,蔡存金 ,方炜杰 (.武汉理工大学土木工程与建筑学院,湖北 武汉430070；.华中科技大学能源与动力工程学院,湖北 武汉 430074)

研究表明,机动车尾气排放物不仅增强了全球的温室效应[1],而且污染城市环境[2],成为城市空气质量恶化的主要原因之一[3-4].为此,越来越多的研究者针对不同环境条件下,各种不同结构的城市街谷中污染物的传播规律开展了理论和实验研究[5].研究表明上游建筑的存在改变了街谷内二次流,减小了街谷内污染物浓度[6];街谷不对称性越大,尾流区浓度越高[7].对街谷形态分析表明街谷高宽比,屋顶几何结构,环境风(以下简称 ACW)的改变均会对街谷内污染物分布的产生影响[8].此外,对该类问题的研究发现模拟和实验结果具有很好的一致性[9-10].

然而目前针对污染物的研究多集中于结构相对单一的模型[11-13],而对具有复杂结构的立体交通中污染物传播特性研究尚属起步阶段.污染物在该种立体交通中的传播机制与结构单一的街谷[14]、孤立建筑[15]、隧道[16-17]等处有很大的不同[18],为此本文构建了一种上部含有交通转盘及直线型机动车道,下部含有敞开式直线型机动车道及封闭式隧道的立体交通模型,探究机动车尾气污染物在该种交通系统中的传播机制.

1 物理数学模型

1.1 物理模型

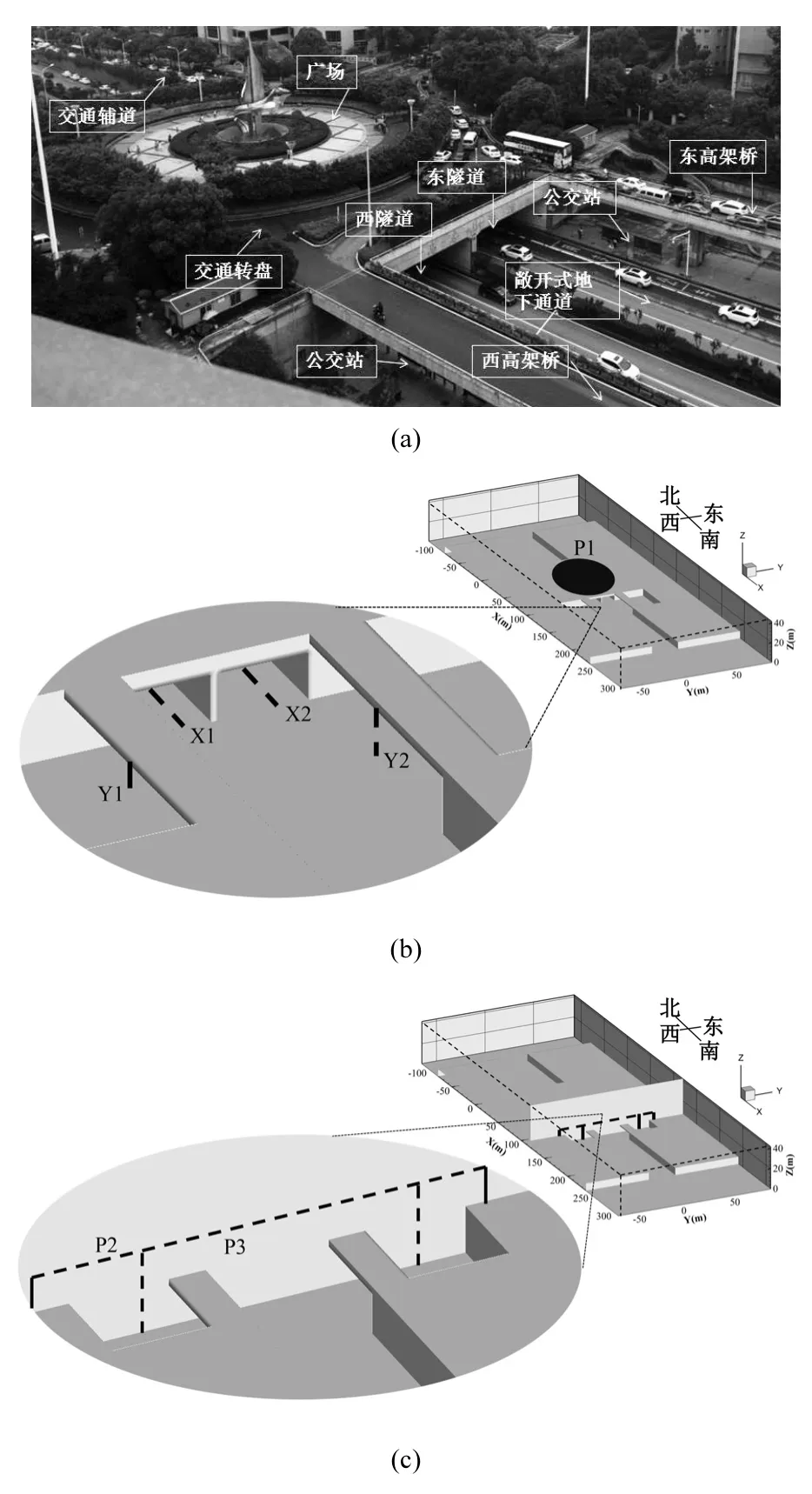
图1 模型实际位置及物理模型Fig.1 Actual position of the model and physical model

以武汉市二环线马房山通道为研究对象,参照实际工程设计尺寸,利用Gambit软件建立全尺寸的几何模型(图1).模型计算域仅选取自然通风的双洞双向市政隧道、交通转盘、交通辅道、敞开式地下通道、下沉式公交站、高架桥等区域,临街建筑物未考虑在内.转盘内圆半径为40m,外圆半径为 45m;交通辅道宽度为 6m;单向市政隧道宽度为 13m,高度为 5m;模型计算域还包括隧道向南,北出口方向分别延伸140m和 80m.市政隧道南侧开口处有两个公交站,地上转盘内圆区为居民和行人活动的广场.

图1(b)、1(c)给出了本文所研究的目标位置,包括图1(b)中转盘广场活动区P1平面,该平面在模型上部距地面1.5m高处.市政双向双洞隧道中心线X1、X2,贯穿整个隧道.还包括图1(c)中P2、P3平面,该平面位于 X=120m 处.图 1(b)中 Y1、Y2这两条线分别位于 P2、P3平面上的东西两侧高架桥处,从地面开始,上至高架桥底部.

1.2 数学模型

采用RNG k-ε模型对计算域进行求解[19],并根据模型流动特性做如下假设：1)计算域内空气物性不发生改变;2)流体为不可压缩流体;3)计算域内流动为湍流并充分发展.

满足条件的连续性方程、动量方程、能量方程如下：

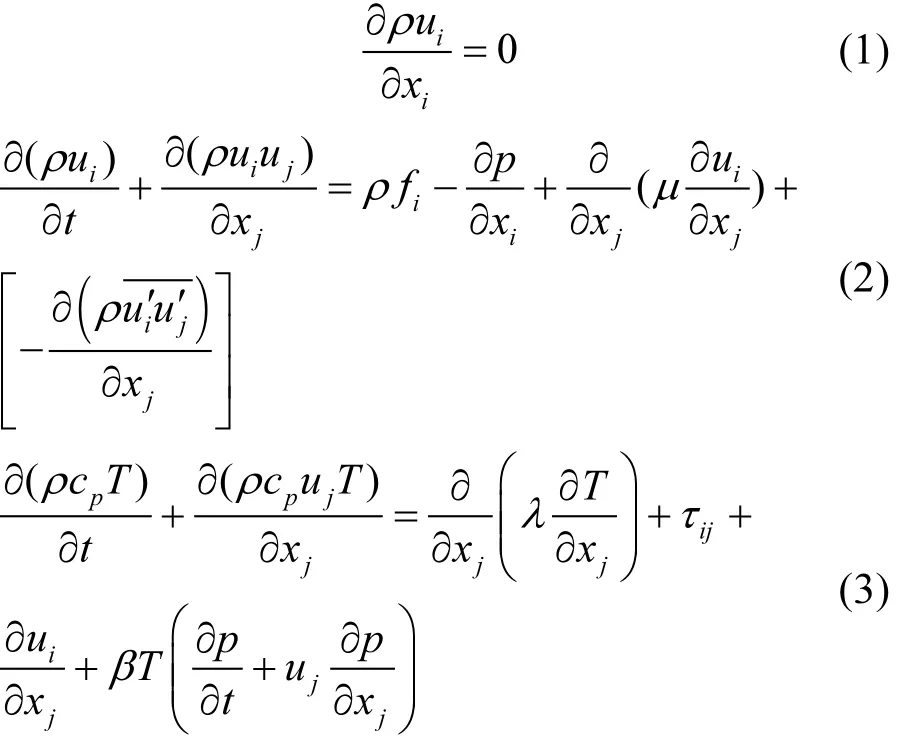
式中：ui是平均流动速度;是脉动速度,ρ是流体密度;μ为运动粘度;为平均雷诺应力,可表示为：

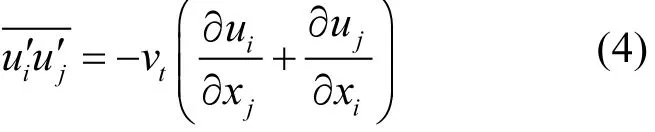
RNGk-ε模型中,湍动能方程 k,湍流耗散率方程 ε为：

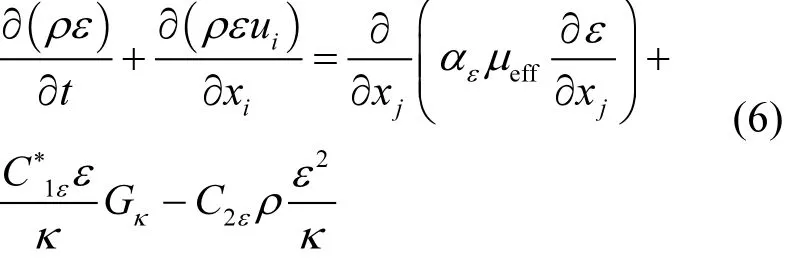
式中：Gk为由平均速度梯度所产生的湍动能;μeff为有效运动粘度,μeff=μ+μt; Cμ、C1ε、C2ε为湍流常数,取值如下：Cμ=0.0845, C1ε=1.42, C2ε=1.68. ακ,αε分别为与湍动能κ和耗散率 ε相对应 Prabdtl数有关的常量,其中 ακ=1.0, αε=1.3.污染物扩散的组分输运方程为：

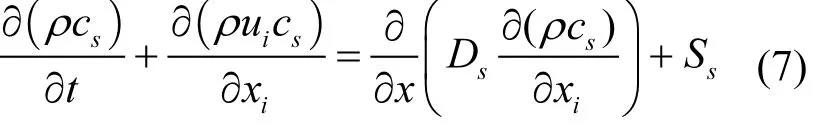
式中：CS为组分S的体积浓度;DS为组分S的扩散系数;SS为系统内部单位时间单位体积内组分 S的产生量.

1.3 边界条件

以环境风为北风时为例,边界条件设定如下：模型中固体壁面均为无滑移壁面;计算域最北侧平面为速度入口,由于交通体系的高度较小为 7m,认定该高度范围内环境风速恒定不发生改变,而交通体系以上计算域对体系内的流动影响较小,为此设定进口风速为恒定风速;计算域最东侧平面、最西侧平面、顶面为对称面;计算域最南侧平面为压力出口,压力值设定为表压0Pa.

当环境风为西风时,边界条件设定与此对应相同,这里不再赘述.

1.4 计算模型

对模型采用方程(1)～(7)进行离散,计算残差设定最大值＜10-5,采用单精度压力耦合半隐式算法求解.连续性方程、N-S方程、RNG k-ε方程的离散等采用一阶迎风差分格式,过程中监控计算域内某一面上的平均速度,确保计算结果的可靠性.

1.5 污染源

模型中污染源设定在机动车道上,机动车排放物作为模型的污染源,模型中设置为体积源,并用CO作为污染物标记物.交通堵塞情况下,污染物传播最终到达稳定状态,强度可设定为4×10-6kg/(m3·s)[20].

2 结果与分析

2.1 模型验证

采用结构化六面体网格对计算域进行划分.考虑到隧道、敞开式地下通道及公交站区域湍流度较高,这3处网格全部被加密为0.5m×0.5m,以此 3个区域为网格中心区向模型计算域四周及上部等比加疏,控制渐进比不大于 1.1.为了测试模型网格的无关性,实际计算过程共进行了两组网格划分,数量分别为 7861356和9645721.模拟结果表明这两组网格系统中,某截面上平均风速相差不超过 3%,据此认为模型网格具备独立性.为节约计算成本,本文选定网格数量为 7861356的模型作为分析依据.

2.2 风向对流动及污染物分布的影响

本节主要讨论环境风向分别为北风和西风时,在恒定的环境风速(以下简称 ACW)ACW=2m/s下,对公交站及转盘广场流场和污染物分布的影响.由于环境风向的改变会对模型中不同位置处的流场造成影响,进一步会影响到该处污染物的分布,为此需探究风向变化的影响.

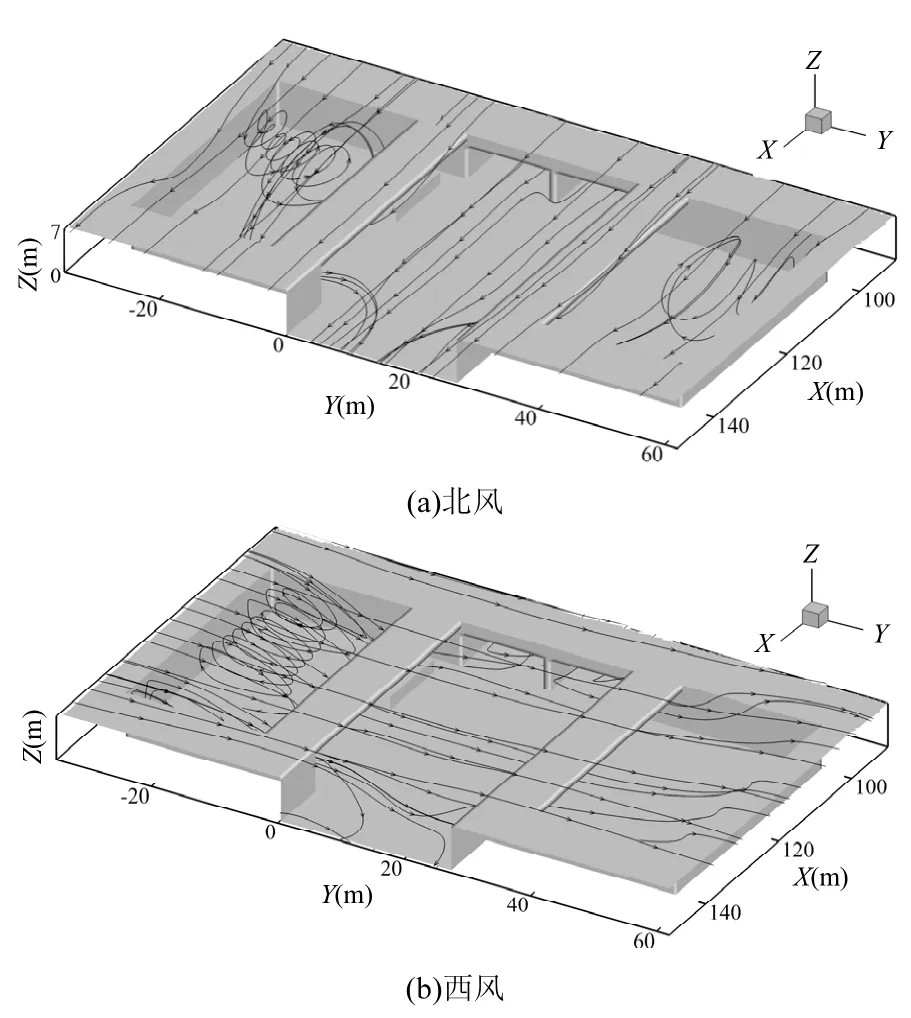
图2 公交站处流线Fig.2 Streamlines at the bus stop area环境风速ACW=2.0m/s

2.2.1 公交站 由图2可知,进入该区域的气流主要分为2部分：一部分直接来自于北侧的隧道,另外一部分来自于流经模型上部地面向下偏转的气流.偏转的气流在下沉式公交站周壁的背风侧形成漩涡.西风时气流在进入敞开式公交站区域时也有部分向下偏转,并在背风侧形成漩涡,此后气流进一步向下游运动,进入东侧的公交站区域、西隧道及南侧的敞开式地下通道.而东隧道内有气流从南侧开口流出,进入东侧公交站区域.环境风向的改变直接改变了该区域内气流流向的变化,从而污染物也随气流进入或流出该区域.

由图3可发现,无论在何种风向下,公交站处的风速受周围几何特征的影响都是很低的,相对而言西风时 P3平面上的平均风速较高,但仅为北风时的1.1倍.北风时由于模型在X方向上左右对称的特点,该处的风场图也是对称的,可以预测北风时污染物分布场图也有类似对称分布的特点.

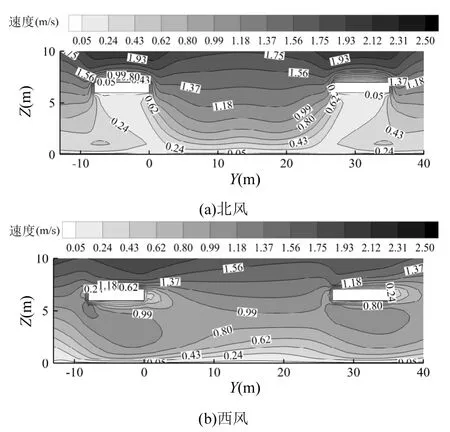
图3 公交站处速度云图Fig.3 Velocity contour at the bus stop area环境风速ACW=2.0m/s

由图 4可发现,北风时污染物的空间分布特性呈现出对称的特点,与上述预测相一致.数值结果表明,北风时P3平面上CO平均浓度为西风时的 3.5倍.这一现象的原因一方面是北风时隧道内污染物被输运到该区域,同时也与上文所述北风时通风情况相对较差有关.另一方面,西风时该区域上游没有污染源,来流风为新鲜空气可以更有效地稀释污染物.由图 1(b)可知 Y1、Y2这两条线位于P3平面,对比两幅图可以发现,在Y1线附近北风时浓度明显高于西风,而在 Y2线附近西风时浓度却高于北风.这主要是由于西风时Y1处,上游来流的新鲜空气冲淡了该处的污染物,而 Y2处于下游,来流风到达该处时已经受到了污染,使得该处的污染加剧,而在北风时 Y1处浓度值介于这两者之间.

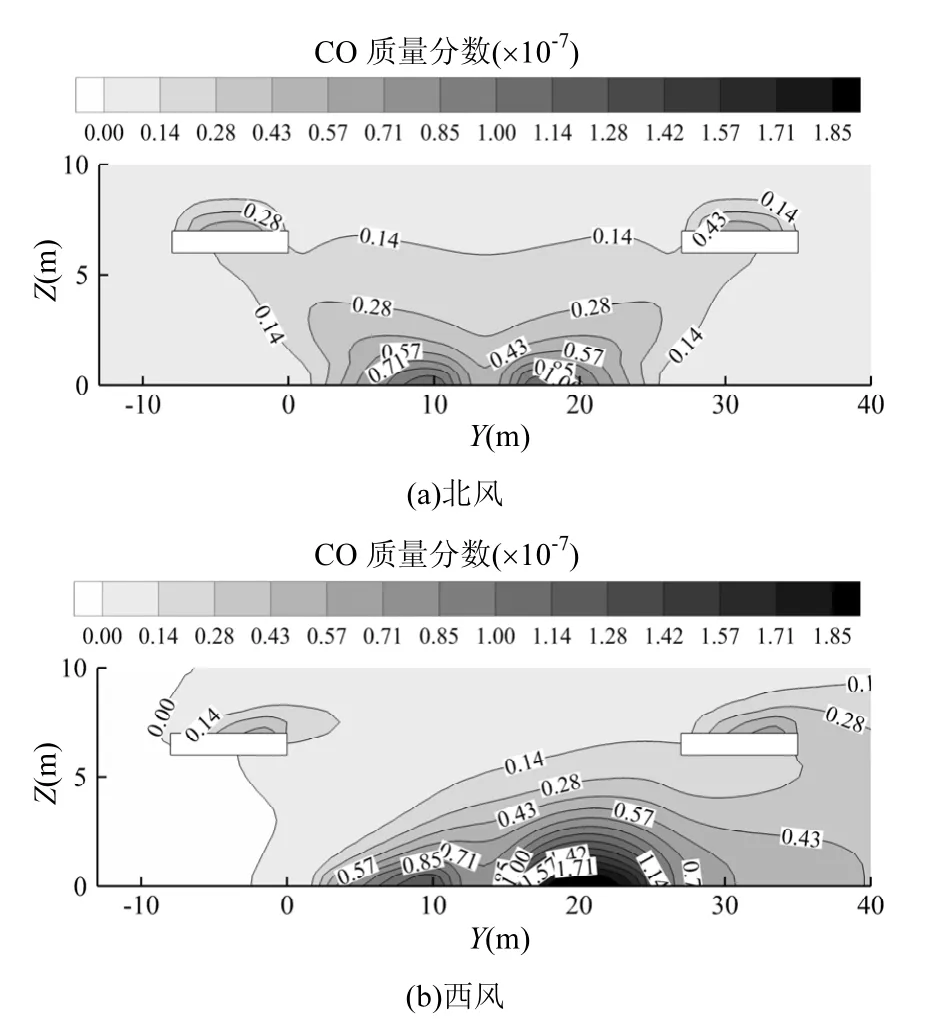
图4 公交站处CO分布场Fig.4 CO distribution at the bus stop area环境风速ACW=2.0m/s

2.2.2 转盘广场活动区 由图5可知,无论在何种风向下,浓度场在相应的风向上对称分布.北风时P1平面上污染物浓度相对于西风时较高,主要是由于北风时除转盘本身污染源外,P1平面上游方向还存在污染源,污染物随气流被输运到该区域;而西风时除转盘本身的污染源外,在上游方向不存在其他污染源,来流风为新鲜的空气可以有效稀释此处的污染物.数值计算结果表明北风时P1平面上污染物平均水平约为西风时的5倍.可见在来流风方向上,上游污染物的迁移对下游的污染相当严重.

2.3 风速对流动及污染物分布的影响

考虑到模型结构的复杂性,计算域内流场和污染物的分布除受风向的影响外,风速的改变也会对计算域内漩涡的形成、影响范围、污染物的堆积与消散等产生影响.

2.3.1 公交站处 由图6看出,首先无论风速怎样变化均会在贴近背风侧和迎风侧的壁面附近形成一大一小2个漩涡.环境风速的大小,对于旋涡中心位置有显著影响,风速越大,漩涡中心越靠近背风侧,这一规律与 Ming等[21]的计算结果相一致.实际上该处结构类似于 AR=0.08的街谷,但旋涡尺度特别是大漩涡尺度远小于 Kastner-Klein等[8]的结果,这主要是由于高架路的存在影响了漩涡的发展.此外,部分贴近西高架底部的气流会从东高架上部流出.可知,受上游高架的影响,流经下游高架下部的风量会减少.

由图7可见,Y1线上风速由下至上呈弓形变化,且环境风速越大,弓形变化幅度越大.这种变化主要由于Y1线上下端分别受高架桥底面及地面的影响,在这两个表面上的速度为 0,在这种上下流动均受阻碍的影响下,速度必然在中间某处达到最大值.模拟结果表明,无论在何种环境风速下,Y1线上风速在Z=4.5m附近达到最大值.而在Y2线上也有类似的特征,但弓形变化不如Y1线上那么规则.这主要是由于西风时,下游的流动受到了上游高架桥的影响,其最大风速值在 Z=5m处达到最大值,且比Y1线上平均增大2.3～8.4%.

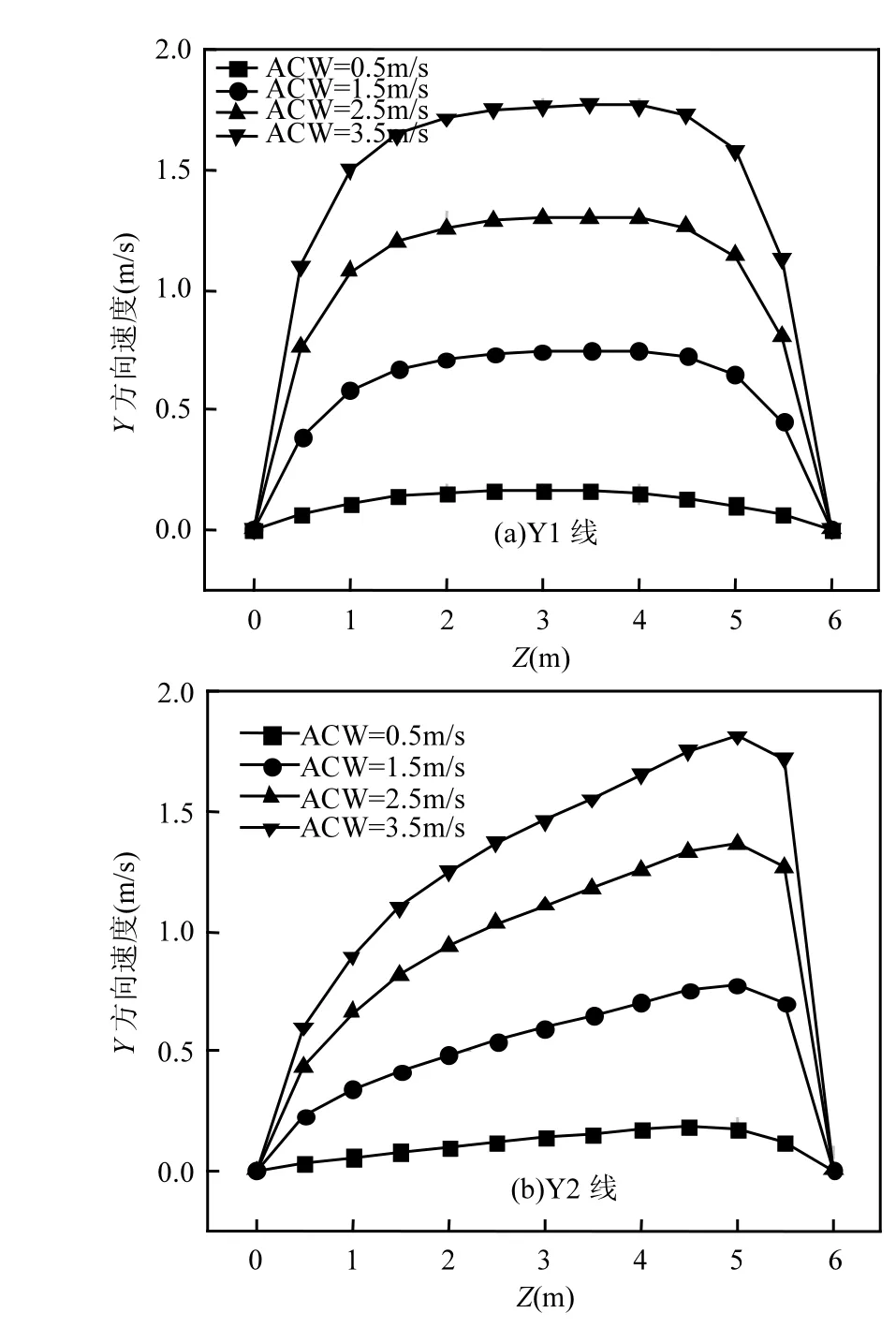
图7 西风时Y1、Y2线上Y方向速度分布Fig.7 Y-velocity distribution at Y1 and Y2 lines in west ACW

图8 中,由于Y1线上来流风是新鲜空气,因此污染物水平除ACW=0.5m/s外,其余风速条件下近乎为 0,可见良好的通风条件对于污染物的稀释扩散是十分有利的;同时,污染物变化曲线与图7(a)风速变化呈反相关关系.在Y2线上也可发现环境风速越大,污染物浓度越低,在环境风由0.5m/s增加至3.5m/s时,Y2线上平均水平减小了95.21%.此外,下游高架下部浓度除受上游污染源影响外,还与如前所述该处通风量的减少有关.对比图 8(a) 和 8(b)可知下游公交站的污染物浓度比上游高出 3个量级,说明西风时由于高架桥的存在,污染物向上层空间传播的量是很少的,2个公交站之间路面上的污染物大量传播到下游公交站.

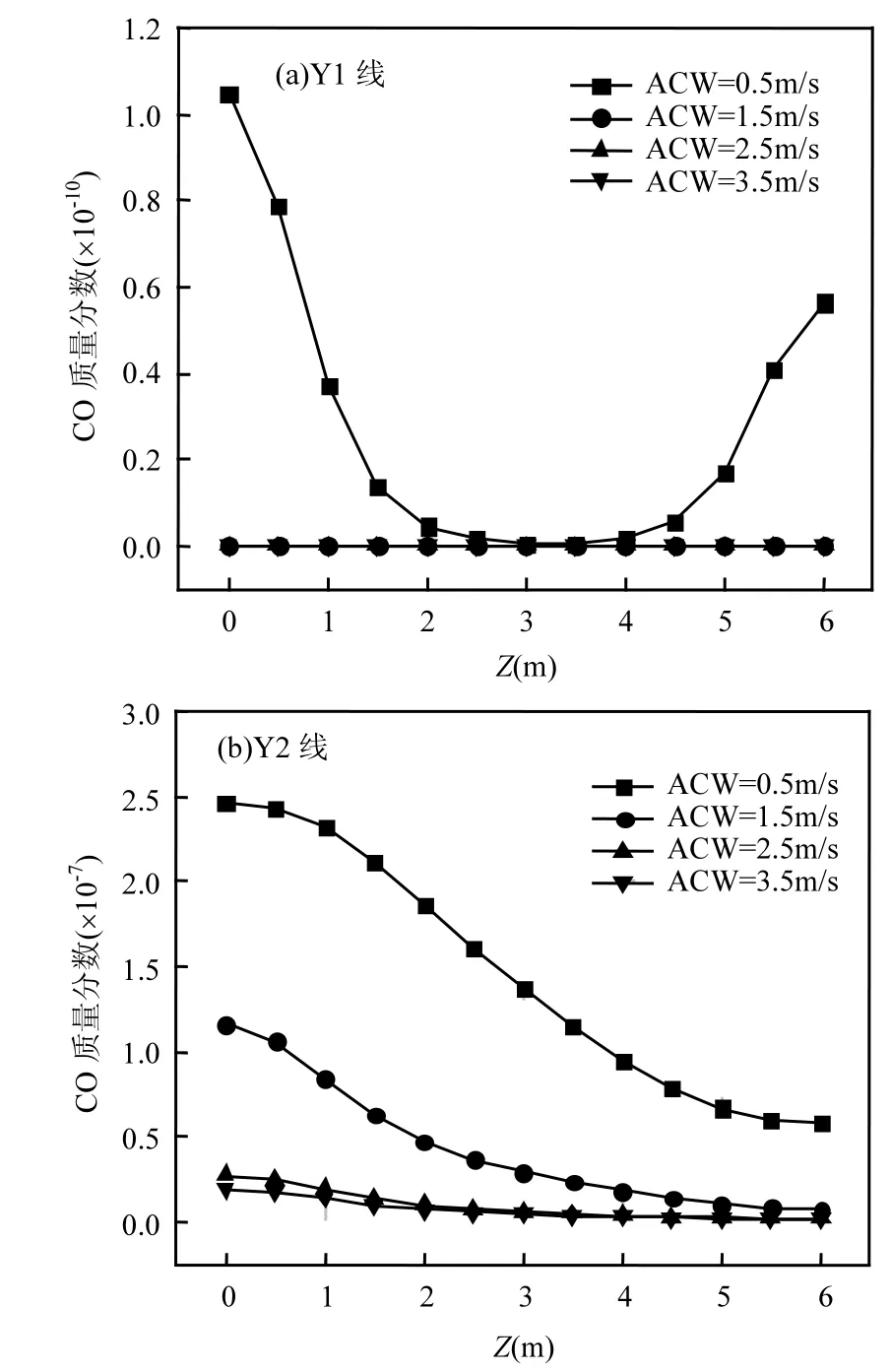
图8 西风时Y1、Y2线上CO分布Fig.8 CO distribution at Y1 and Y2 lines in west ACW

2.3.2 市政隧道 环境风为西风时,由图9可知,这 2个隧道内的风速大致呈现随环境风速的增大而增大,且在临近隧道两侧开口区速度均有显著的变化,这种变化在环境风速越大时越明显.由于临近隧道开口区流场的分布受外界影响很大,环境风速越大开口区速度分布的不均匀性也越大,表现为开口区的变化特点.对比图 9(a)和 9(b)可知,同样的环境风速下西隧道内速度相对较大,数值计算结果表明X1线上速度平均值为X2线上的1.65～4.41倍.基于此也可以预测西隧道内污染物水平相对较小.

图 9(a)可知,西隧道内风速是负值,表明隧道内气流的运动方向由南向北,临近隧道南侧开口局部区域有速度正值的出现也主要受开口区复杂流场的影响.而图 9(b)则表现出隧道内空气流向因外界环境的变化而发生改变的现象,即在ACW=0.5,3.5m/s时,东隧道内空气整体表现出由南向北运动,其余两种环境风速下由北向南运动.究其原因主要是与隧道南北两侧相连接区域的几何特性不同,致使在垂直于隧道方向的环境风向下当风速发生变化时,引起了下游隧道内流场分布发生了巨大的变化.在临近隧道开口区流场的分布是极为复杂的,关于自然通风隧道开口区流场的变化特点及对隧道内空气流动的影响,我们将在下一步进行重点研究.

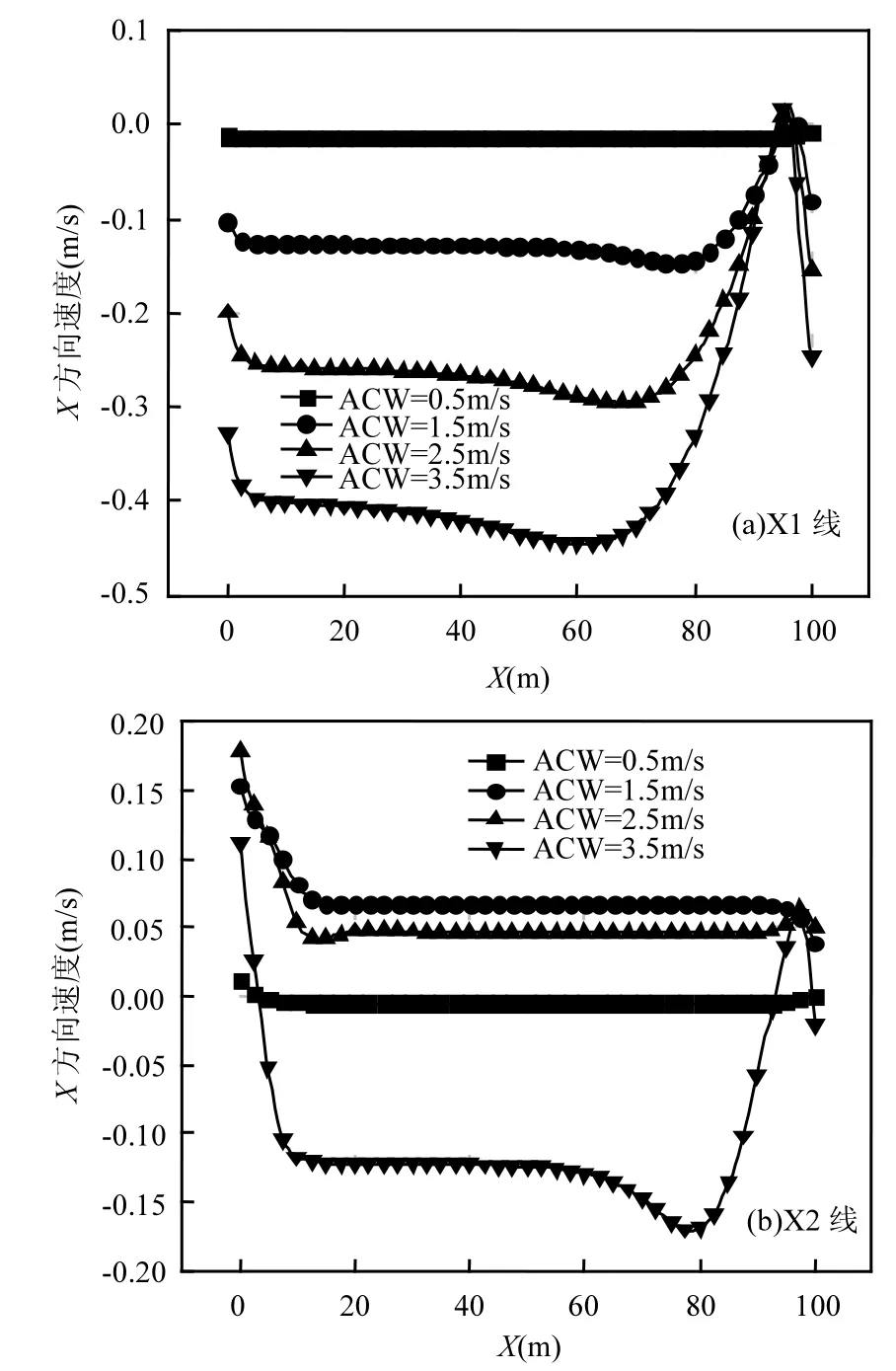
图9 西风时X1、X2线上速度分布Fig.9 Velocity distribution on X1 and X2 lines in west ACW

图10 中西隧道内污染物水平相对较低,这一点与上述分析西隧道内风速较大的特点相对应.污染物浓度的变化及其形成原因大致经历这样一个过程：外界风进入隧道稀释隧道污染物的同时,自身的污染物浓度也越来越高,这样就表现为污染物浓度沿隧道内气流方向越来越高,并在下游某处聚集达到顶峰,紧接着再往下游运动又受隧道开口区气流的影响,风速增大污染物浓度降低.结合图9可知,隧道内风速越小,污染物浓度也就越大,污染物的堆积现象也就越明显;而隧道内风速越大,污染物浓度的峰值位置越靠近下游开口.由于在ACW=0.5,3.5m/s时东隧道内气流是由南向北的,因此污染物浓度会在隧道北半段达到峰值;而在ACW=1.5,2.5m/s时与此相反.

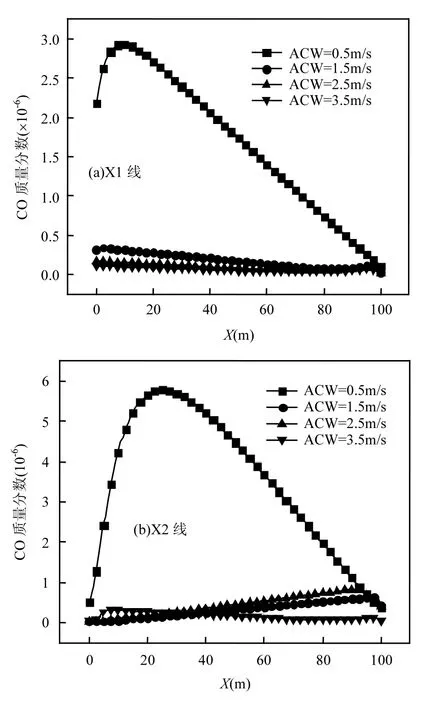
图10 西风时X1、X2线上CO质量分数Fig.10 Mass fraction of CO on X1 and X2 lines in west ACW

2.4 展望

值得指出,本文仅分析了交通堵塞时环境风的变化对该种立体交通体系中流场及污染物分布的影响.然而在交通顺畅时,车辆的快速行进引起周围空气运动的作用是不能忽略的[22].而且周围建筑及植物绿化带对污染物的扩散传播也值得探索[23].此外,因太阳辐射而引起的受热局部不均匀对结果的影响也很大.对于这些因素的影响将会作为以后工作中予以考虑.

3 结论

3.1 当环境风垂直于车流方向流过复杂立体交通体系时,上、下游高架桥和下沉式公交站的特殊空间结构对系统中的空气流动和污染物传播特性造成显著影响,公交站之间路面上的污染物很难迅速向上层空间稀释传播,下游公交站的污染水平比上游公交站高出三个量级.

3.2 转盘广场处,污染物浓度受风向的影响较大,北风时该处平均浓度是西风时的5倍.

3.3 当环境风向垂直于隧道方向时,由于隧道开口两侧连接区域几何特征的不同,环境风速的变化引起了隧道内空气流动方向的改变,同时污染物沿空气流通方向堆积,但在开口处却迅速降低.

[1]De_Richter R, Ming T, Davies P, et al. Removal of non-CO2greenhouse gases by large-scale atmospheric solar photocatalysis[J]. Progress in Energy & Combustion Science, 2017,60：68-96.

[2]Yassin M F, Ohba M. Experimental study of the impact of structural geometry and wind direction on vehicle emissions in urban environment [J]. Transportation Research Part D, 2012,17(2)：161-168.

[3]Karakolios E A, Vosniakos F K, Mamoukaris A, et al. Vehicle emissions in the city of Leptokaria (Greece) and its contribution to the atmospheric air and noise pollution [J]. Fresenius Environmental Bulletin, 2013,22(3)：879-883.

[4]杨笑笑,汤莉莉,胡丙鑫,等.南京城区夏季大气 VOCs的来源及对 SOA的生成研究——以亚青和青奥期间为例 [J]. 中国环境科学, 2016,36(10)：2896-2902.

[5]Sabatino S D, Buccolieri R, Salizzoni P. Recent advancements in numerical modelling of flow and dispersion in urban areas： A short review [J]. International Journal of Environment &Pollution, 2013,52(3/4)：172-191.

[6]朱 强,亢燕铭,杨 方,等.上游建筑对街道峡谷内流场和污染物分布特征的影响 [J]. 中国环境科学, 2015,35(1)：45-54.

[7]杨 方,钟 珂,亢燕铭.街道峡谷对称性对污染物扩散的影响[J]. 中国环境科学, 2015,35(3)：706-713.

[8]Kastner-Klein P, Plate E J. Wind-tunnel study of concentration fields in street canyons [J]. Atmospheric Environment, 1999,33(24/25)：3973-3979.

[9]Chang C H, Meroney R N. Numerical and physical modeling of bluff body flow and dispersion in urban street canyons [J].Journal of Wind Engineering & Industrial Aerodynamics, 2001,89(14)：1325-1334.

[10]Gousseau P, Blocken B, Van Heijst G J. Large-Eddy Simulation of pollutant dispersion around a cubical building： analysis of the turbulent mass transport mechanism by unsteady concentration and velocity statistics [J]. Environmental Pollution, 2012,167(6)：47.

[11]胡 伟,钟 秦.壁面加热作用对街道峡谷污染物扩散的影响[J]. 中国环境科学, 2009,29(9)：908-913.

[12]王 乐,张云伟,顾兆林.动态风场及交通流量下街道峡谷内污染物扩散模拟 [J]. 中国环境科学, 2012,32(12)：2161-2167.

[13]田 丰,余 志,蔡 铭,等.双车道街道峡谷内污染物扩散的模拟 [J]. 中国环境科学, 2007,27(5)：604-607.

[14]Michioka T, Takimoto H, Ono H, et al. Effect of Fetch on a Mechanism for Pollutant Removal from a Two-Dimensional Street Canyon [J]. Boundary-Layer Meteorology, 2016,160(1)：185-199.

[15]谢海英,陈康民.孤立与非孤立城市街道峡谷内污染物扩散 [J].环境污染与防治, 2007,29(8)：595-598.

[16]王子云,谢朝军,唐上明,等.城市隧道双洞口污染物扩散模拟分析 [J]. 铁道工程学报, 2010,27(12)：69-72.

[17]季 亮,谭洪卫,王恩丞,等.城市中心区不同隧道排风井形式的污染物扩散比较研究 [J]. 建筑科学, 2009,25(6)：76-79.

[18]Tominaga Y, Stathopoulos T. CFD simulation of near-field pollutant dispersion in the urban environment： A review of current modeling techniques [J]. Atmospheric Environment, 2013,79(11)：716-730.

[19]Shih T H, Liou W W, Shabbir A, et al. A new k - eddy viscosity model for high reynolds number turbulent flows [J]. Computers &Fluids, 1995,24(3)：227-238.

[20]Tsai M Y, Chen K S. Measurements and three-dimensional modeling of air pollutant dispersion in an Urban Street Canyon [J].Atmospheric Environment, 2004,38(35)：5911-5924.

[21]Ming T, Gong T, Peng C, et al. Pollutant Dispersion in Built Environment [M]. Springer Singapore, 2017.

[22]刘红年,蒋维楣,徐振涛,等.城市中心街道交通隧道废气排放模拟 [J]. 中国环境科学, 1998,18(6)：494-497.

[23]钟 珂,亢燕铭,王翠萍,等.城市绿化对街道空气污染物扩散的影响 [J]. 中国环境科学, 2005,25(6)：6-9.