四自由度机器人抓取运动目标建模与轨迹规划

（西安工程大学 电子信息学院，西安 710048）

0 引言

随着制造业自动化需求的提高，机器人已被广泛应用到各行各业，随之对机器人自主抓取的工作精度和运动平稳度的要求也越来越高[1]。自主抓取系统的核心是抓取规划器的建立，轨迹规划是对机器人的运动路径进行描述，使其运行更平稳[2]，其大多数轨迹规划算法主要是利用抛物线、多项式以及不同曲线相结合[3]。文献[4]利用Matlab对Dobot机器人进行正逆运动学分析建模和五次多项式插值轨迹规划仿真，为实际应用研究和开发提供了理论依据。文献[5]分析比较了在工业机器人轨迹规划中采用三、五次多项式的运动性能，结果表明，五次多项式的轨迹规划效果优于三次多项式样条。文献[6]采用五次B样条曲线插值方法进行关节轨迹规划，仿真结果表明，该方法运动性能显著优于传统的三次样条轨迹规划。在实际工程应用中，常采用五次多项式对关节轨迹进行规划，该算法相对较简单，运算量不大，但该算法关节位移变化大，任意关节点参数的变化都会造成机械臂的振动和冲击，影响机器人工作的平稳性，使五次多项式的应用受到了局限[7,8]。

本文研究了一种四自由度机器人抓取运动目标的建模与轨迹规划，并进行运动学分析；采用七次多项式对抓取运动目标过程进行轨迹规划，使抓取过程顺利完成，并利用Matlab中Robotics工具箱对四自由度机械手和抓取过程进行建模仿真，结果表明，四自由度机器人自主抓取规划满足要求，能够对运动目标进行稳定和准确地到抓取，有效地降低了硬件开发成本且有利于运动控制。

1 四自由度机器人的运动学分析

四自由度机器人可看成由一系列刚体通过关节连接而成，这些刚体通常被称为连杆，连杆共有4个基本属性参数。其中关节1，2，4是旋转关节，关节3是垂直升降关节。图1为四自由度机器人本体结构，根据改进的D-H表示法，建立坐标系的简化图，如图2所示。根据机械臂的结构和连杆坐标系，可得出连杆参数和关节变量[9]，如表1所示。

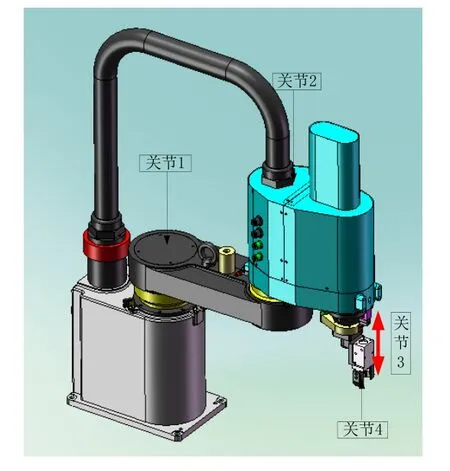
图1 四自由度机器人本体结构

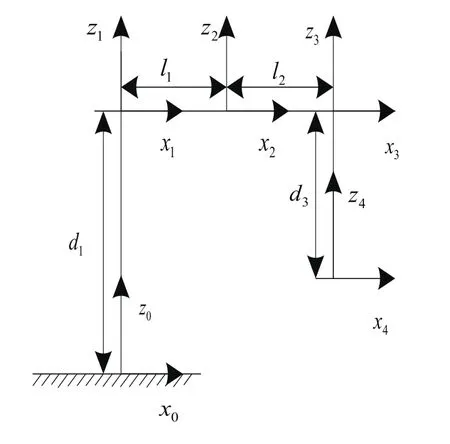
图2 四自由度机器人的连杆坐标系

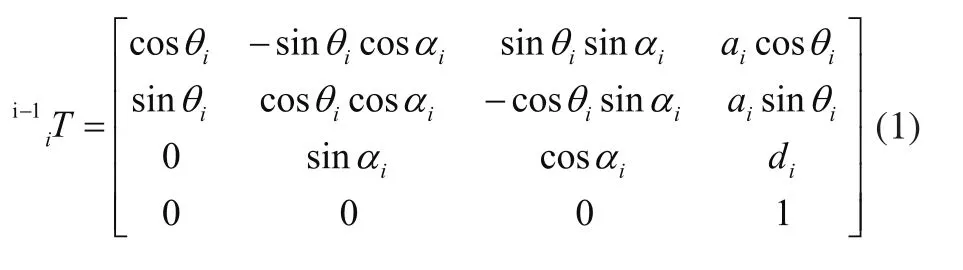
将四自由度机器人各连杆变换矩阵相乘，可得到末端执行器的位姿方程为：

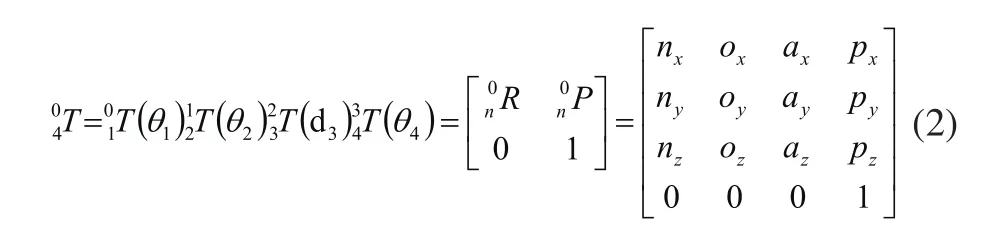
2 运动学建模与仿真

首先，构建四自由度机器人的模型是进行仿真首要完成的任务，采用机器人工具箱构建模型，以表1中的D-H参数为依据来构建四个关节，然后利用工具箱提供的Link和SerialLink函数将各关节有机组合来实现整个机械臂的构建。在Matlab中利用Robotics Toolbox中提供的Link和SerialLink函数对四自由度机械臂进行建模，建立的四自由度机器人模型如图3所示。

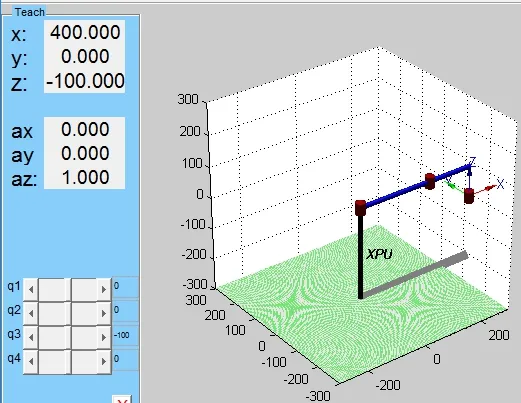
图3 四自由度机器人三维图

图3左侧是滑块控制，右侧是机器人是三维模型。x，y，z表示末端执行器的位置，ax，ay，az表示末端执行器的姿态，各关节的初始位置q=[0 0 0 0]，q1，q2，q3，q4为四自由度机器人相应的四个关节角度值。通过移动滑块，可直观的观测到机器人不同的位姿。

利用函数fkine计算正运动学解，仿真结果如下：

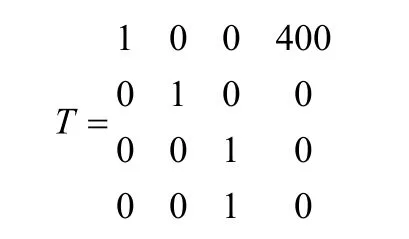
各关节角度都为零，直角坐标R(x,y,z)为(400,0,0)是一致的，验证了在第1.1节中采用机器人工具箱构建的四自由度机器人模型的正确性。

3 四自由度机器人轨迹规划

机器人模型构建完成后，通过计算机控制，机器人从初始点运动到目标点进行抓取操作，这个过程需要进行运动学轨迹规划。为了使抓取更加合理准确，本文采用Matlab中机器人工具箱，在关节空间中对点到点的路径进行规划。已知在操作空间中的两点，用逆运动学将笛卡尔坐标映射到关节空间，再对其进行多项式插值[11]。

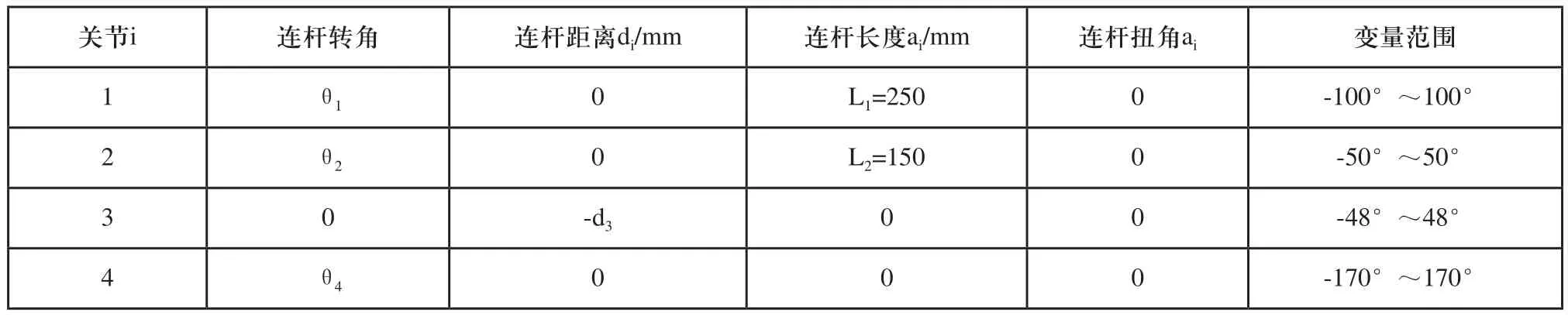
表1 四自由度机器人D-H参数表

3.1 七次多项式规划

一般基于多项式插值的运行曲线比基于线性插值的运动轨迹速度、加速度曲线更为光滑连续没有突变，即机器人轨迹精度较好[12]。若需机器人各个关节运行平稳，应选多项式插值算法，其中七次多项式插值比三次、五次更平稳，运动性能更优，因而本文采用七次多项式进行关节空间中轨迹规划，设七次多项式：

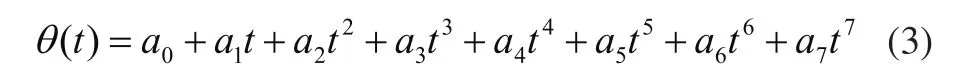
各关节在起点和终点的位置、速度、加速度和冲击的约束条件为：

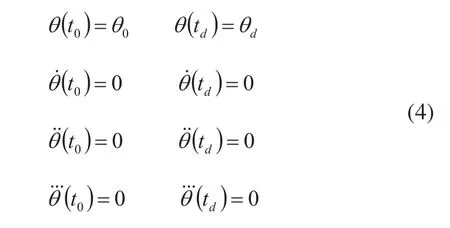
对式(3)求一阶、二阶、三阶导可得：

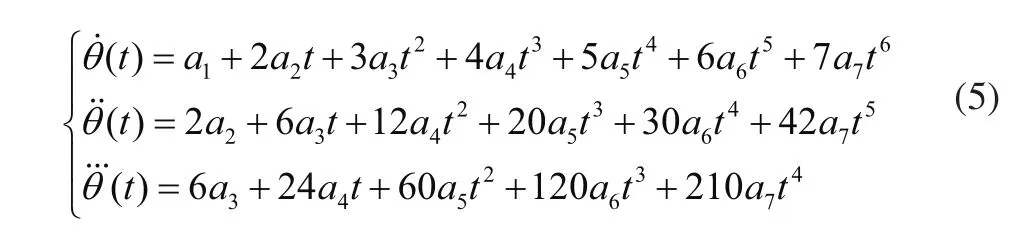
联立式(3)～式(5)，可得：

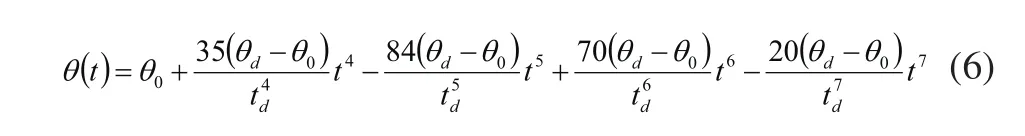
式(6)是该关节的七次多项式的轨迹函数，它确定了从θ0到θf任意时刻的关节位置。该关节的角速度和加速度均为抛物线，其函数公式如式(7)所示：

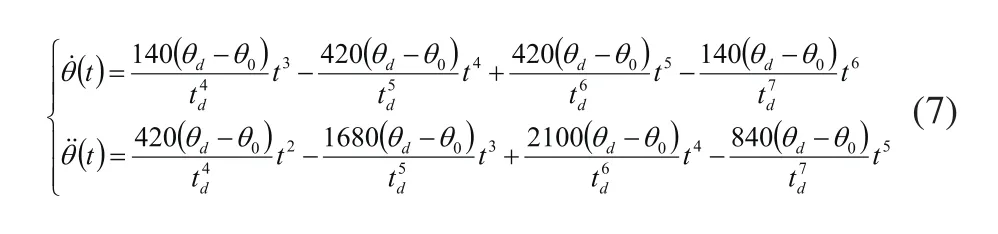
3.2 轨迹规划的任务要求

本文四自由度机器人主要实现的是对运动目标的抓取，动作较为简单，所以采用PTP轨迹规划方法。设抓取点为A，首先运动到抬高点B，然后再将B点视为起始点，运动到降落点C，最后将C点视为起始点，继续运动到放置点D。机器人末端执行器轨迹路径取决于抓取运动目标的任务要求，即从抓取点A出发到达放置点D，中间经过抬高点、降落点。现设定A（228，50，-337）、B=（228，50，-282）、C=（-65，395，-315）、D=（-65，395，-337）。从A点到B点，以及C点到D点，这两段运动过程均为机器人做上升或下降的垂直运动，关节1,2,4位姿保持不变，只有关节3的姿态发生变化。B、C点的存在就为使机器人末端运行的路径光滑且连续并尽量减少对电动机的冲击，故BC段是本文轨迹规划的主要部分。抓取轨迹路线如图4所示。

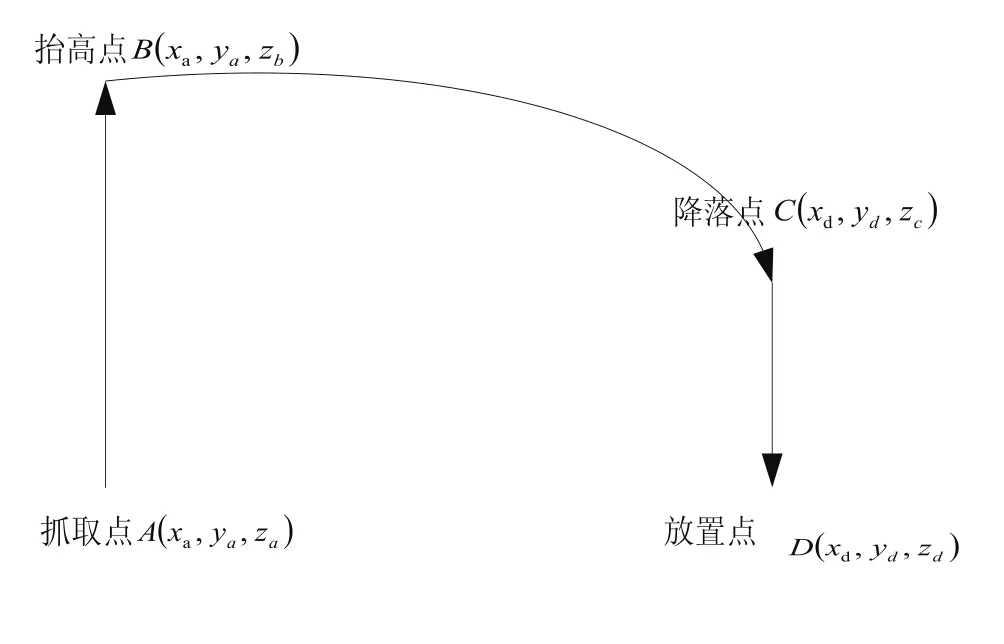
图4 抓取过程中轨迹路线

根据四点的坐标通过逆运动学求解出各点的各个关节转角qA，qB，qC，qD，即qA=[0.8433 -1.9898-337.0000 0]、qB=[0.8433 -1.9898 -282.0000 0]、qC=[1.7321 0.0046 -315.0000 0]、qD=[1.7321 0.0046-337.0000 0]，然后，根据七次多项式的约束条件，求解出各关节的插值函数，确定机器人预期的轨迹路径。

4 建模与仿真

在Matlab环境下，利用机器人工具箱建立四自由度机器人结构模型，设定四自由度机械臂的仿真时间是3s，即已知从抓取点A运行到放置点D的空间坐标，利用ikine函数可求出各个关节角，采用七次多项式插值的轨迹规划算法对从A到D点的抓取过程进行仿真，本文主要对BC段进行轨迹规划，如图5所示。

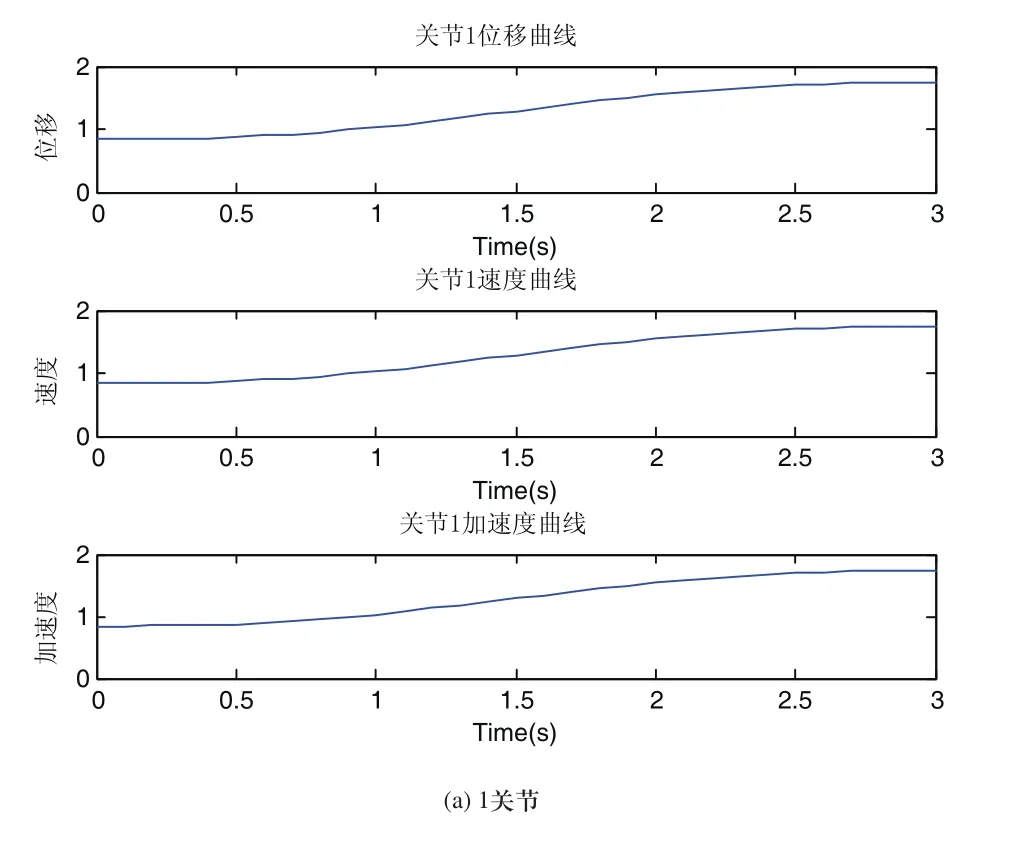
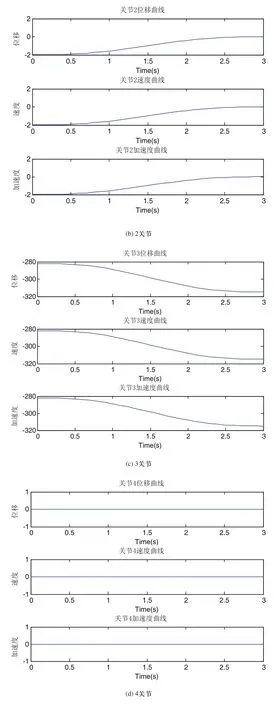
图5 抓取过程中BC段各关节的变化曲线图

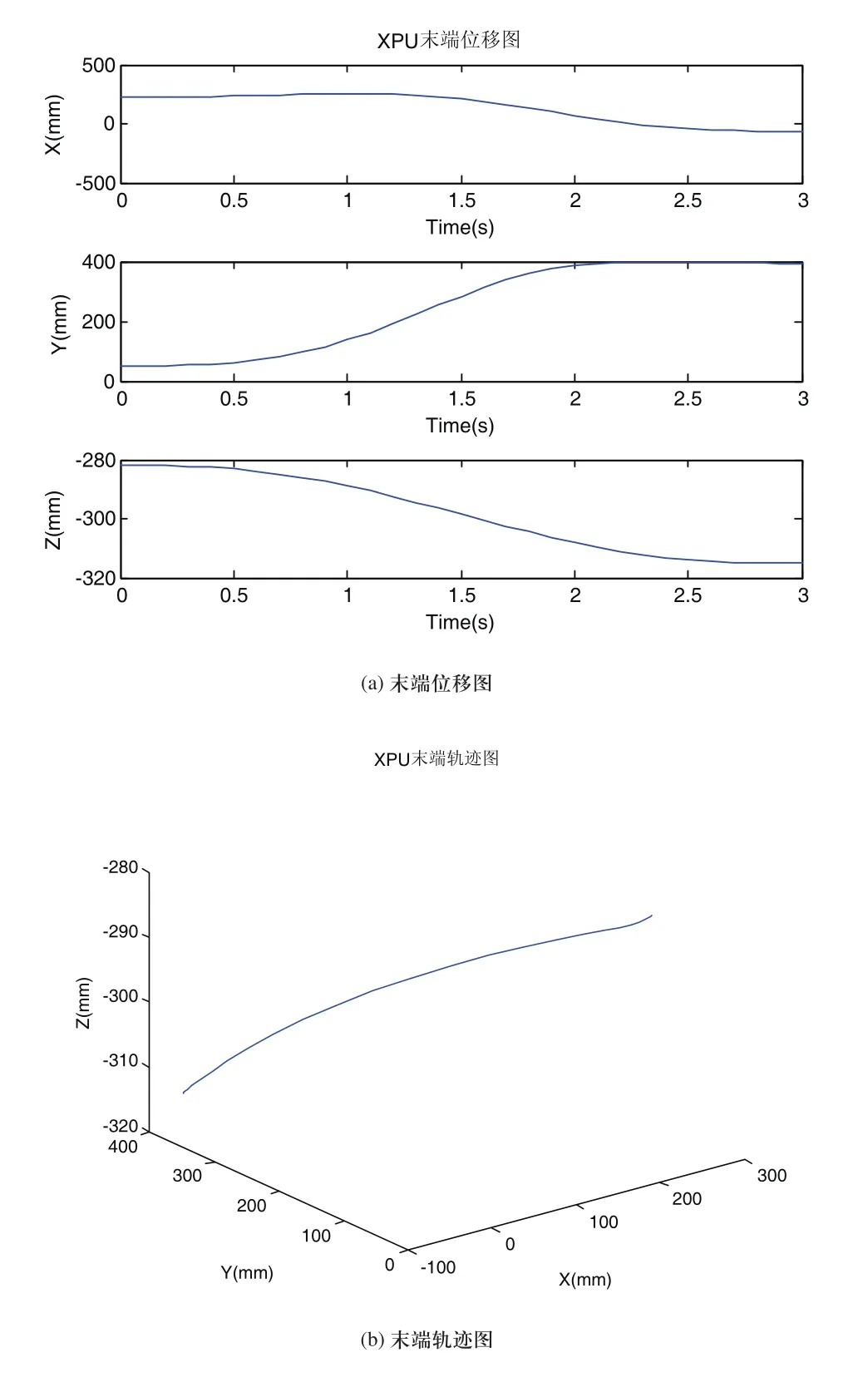
图6 BC段末端位移图和轨迹曲线

图5为各个关节的位移、速度和加速度的变化曲线，运行的速度，加速度均平滑，没有突变，运行连续且平稳；在轨迹规划过程中各关节运动状态正常，各连杆均未出现错位情况，符合抓取过程中轨迹规划的要求。图6为四自由度机械人末端在BC段运动的位移图和轨迹曲线均变化连续没有突变，故在对运动目标抓取过程中，实现了机器人平稳的抓取轨迹规划。

5 结论

为使四自由度机器人的运行更加平稳，提高轨迹规划精度。本文提出采用七次多项式插值算法对给定的PTP的作业要求进行轨迹规划，在Matlab平台下仿真实现机器人轨迹规划。实验结果表明，在抓取运动目标过程中，各关节位移、速度及角加速度随时间变化曲线连续没有突变，实现了机器人运行平稳且连续，提高了机器人运动性能，是一种稳定可靠的轨迹规划方法。为以后四自由度机器人的研究和开发提供了理论依据，实验的后期工作则是将该方法在四自由度机器人平台上用C++语言编程，实现对机器人各个关节的轨迹规划。

[1]战茜,屠大维.移动机器人自主抓取作业[J].计算机应用,2016,36(S1):95-98.

[2]祁若龙,周维佳,王铁军.一种基于遗传算法的空间机械臂避障轨迹规划方法[J].机器人,2014,36(3):263-270.

[3]Bearee R. Olabi A. Dissociated jerk-limited trajectory applied to time-varying vibration reduction[J].Rob Comput Intergr Manuf,2013,29(2):444-453.

[4]赵智勇,王冬青.Dobot机器人运动学分析及建模仿真[J].青岛大学学报(工程技术版),2017,32(1):52-57.

[5]刘子贵.基于关节空间工业机器人轨迹规划的研究与仿真[J].机械工程与自动化,2017,3:59-61.

[6]李小霞,汪木兰,刘坤等.基于五次B样条的机械手关节空间平滑轨迹规划[J].组合机床与自动化加工技术,2012,8:39-42.

[7]赵智勇,王冬青.Dobot机器人运动学分析及建模仿真[J].青岛大学学报（工程技术版）,2017,32(1)52-57.

[8]Y.-l. Yang, Y.-d. Wei, J.-q. Lou，et al.Nonlinear dynamic analysis and optimal trajectory planning of a high-speed macro-micro manipulator[J].Journal of Sound and Virbration 2017,45:112-132.

[9]张蕾,韦攀东,李鹏飞,等.采用神经网络算法的多指机械手织物抓取规划[J].纺织学报,2017,30(1):132-139.

[10]潘磊,钱炜,张志艳,等.四自由度机械臂运动学分析及Matlab仿真[J].机械科学与技术,2013,32(3):421-425.

[11]Saeed B .Niku .Introduction to Robotics[M].BEIJING:Publishing House of Electronics Industry,2013.

[12]孙瑛,程文韬,李公法,等.关节型机器人轨迹规划算法及轨迹规划研究现状[J].长江大学学报（自然版）,2016,13(28):32-38.