Bernstein Bezout矩阵与多项式的惯性*

李 珊， 吴化璋

(安徽大学 数学科学学院，合肥 230601)

0 引 言

Bezout矩阵在多项式与线性控制系统理论、结构矩阵理论等领域有着广泛的应用[1-4]，近些年来，经典的Bezout矩阵被推广到一些多项式基下进行研究[5-8].而Bernstein多项式基是一类特殊且重要的多项式，在计算机辅助几何设计中的Bezier曲线方面有着重要应用[9-11]，自然地受到一些数学研究者的重视.

最近，在文献[12]讨论了Bernstein Bezout矩阵与Bernstein多项式基下的(广义)可控制型/可观测型矩阵之间的相互联系.本文是文献 [12]的继续，将讨论Bernstein Bezout矩阵在多项式的惯性和稳定性方面的应用.

本文将在复数域范围来讨论，且多数记号将继续沿用文献[1]中的记号.用n[x]表示复数域上次数不超过n-1的线性多项式空间.令：

π(x)=(1，x，…，xn-1)T

构成的n维向量.又令T是π(x)与B(x)之间的过渡矩阵，满足

TB(x)=π(x)

(1)

又设a(x)和b(x)分别是它们对应的关于标准幂基的表达式，即

那么，由a(x)与b(x)生成的关于标准幂基的双线性函数：

所确定的矩阵B(a，b)=(zij)为a(x)和b(x)生成的经典Bezout矩阵，有时也记作B(f，g).而由f(x)与g(x)生成的关于Bernstein多项式基的双线性函数：

TTB(a，b)T=B(b)(f，g)

(2)

如果g(x)≡b(x)=1，那么

B(b)(f，1)=TTB(a，1)T

(3)

若令S(a)=B(a，1)，S(b)(f)=B(b)(f，1)，则式(2)可简写为

S(b)(f)=TTS(a)T

(4)

称为多项式p(x)(关于标准幂基)的第二伴侣矩阵，它 (关于Bernstein多项式基) 的广义伴侣矩阵定义为

C(b)(p)=T-1C(p)T

(5)

由文献[12]，并结合式(4)、式(5)知，Bernstein Bezout矩阵B(b)(f，g)有如下形式的Barnett型分解公式：

B(b)(f，g)=S(b)(f)g(C(b)(f)T)

1 经典Bezout矩阵与多项式惯性

特征值的稳定性问题通常是根据一个矩阵的特征多项式的零点分布来判定的，为了避免特征多项式系数的计算造成的不精确性，人们常利用Lyapunov定理来判定.本节将介绍经典的Fujiwara-Hermite定理和Routh-Hurwitz定理[3]，这两个定理就是通过利用经典的Bezout矩阵所满足的Lyapunov定理来获得一个多项式的零点分布理论.

先介绍一些记号：三元非负整数组

In(p)={π(p)，v(p)，δ(p)}

表示复系数多项式p(x)关于虚轴的惯性分布，其中π(p)，v(p)和δ(p)分别表示p(x)的具有正实部，负实部和零实部根的个数(包括重数).特别地，如果π(p)=δ(p)=0，则称p(x)关于虚轴是稳定的.对应地，三元非负整数组：

In′(p)={π′(p)，v′(p)，δ′(p)}

表示p(x)关于实轴的惯性分布，其中π′(p)，v′(p)和δ′(p)分别表示p(x)的在开的上半平面，开的下半平面和实轴上零点的个数(包括重数).很显然，

{π′(p(-ix)，v′(p(-ix))，δ′(p(-ix))}=

{π(p(x))，v(p(x))，δ(p(x))}

对一个复矩阵Α的惯性，通常采取以上类似的记号并赋予类似的含义.即

In(A)={π(A)，v(A)，δ(A)}

In′(A)={π′(A)，v′(A)，δ′(A)}

分别表示矩阵A的特征值关于虚轴和实轴的惯性分布.称复矩阵A是Hermite矩阵，如果A=A*，其中A*表示矩阵A的共轭转置.用记号A>0(≥0) 表示矩阵A是Hermite正定(半正定)的.

下面的引理来自文献[3]，是Lyapunov关于矩阵惯性理论的一个推广.

引理1 如果A∈n×n，δ(A)=0，且对Hermite非奇异矩阵H∈n×n满足如下方程：

AH+HA*=W≥0

那么In(A)=In(H).

由此引理，能推导出如下经典的Fujiwara-Hermite稳定性准则和惯性定理.

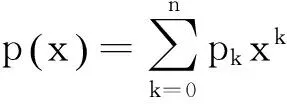
2 Bernstein Bezout矩阵与多项式惯性

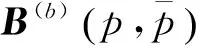
定理3 假设由多项式：

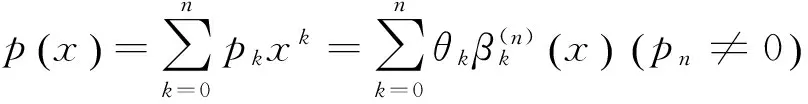
证明首先，容易检验

其中

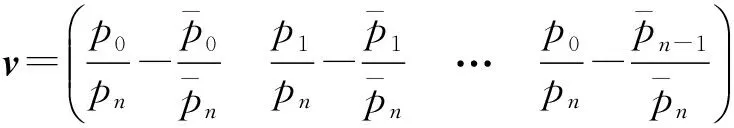
可得：

(5)

其中，容易算出矩阵：

对式(6)作一些变换，并写成如下形式：

(7)

利用式(2)，式(7)又等价于

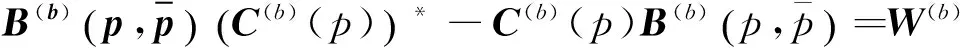
(8)

其中矩阵W(b)=TTWT≥0，这是由于过渡矩阵T是非奇异实矩阵.矩阵方程式(8)可写成：

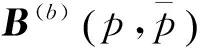
δ(-iC(b)(p))=0

根据引理1，有

另一方面，

In(-iC(b)(p))=In′(C(b)(p))=In′(p)

故定理得证.

下面给出经典的Routh-Hurwitz惯性定理在Bernstein多项式基下的推广形式.

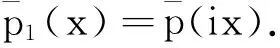
(7)

利用下面的等式：

B(ix)=T-1π(ix)=T-1Dπ(x)=

T-1DTT-1π(x)=T-1DTB(x)=FB(x)

其中，D=diag(1，i，…，in-1)，F=T-1DT，那么式(9)可写成：

(10)

注意到F=T-1DT，那么

其中

C=diag(1，(-1)1，…，(-1)n-1)

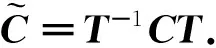
再用引理1可得

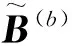
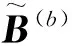
这就获得了下面的结果，此定理可以看做是经典的Routh-Hurwitz惯性定理和稳定性准则在Bernstein多项式基下的推广.

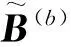
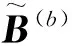
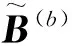
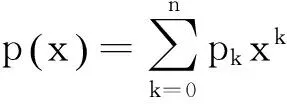
[1] BARNETT S.Polynomials and Linear Control System[M].New York： Marcel Dekker，1983

[2] HEINIG G，ROST K.Algebraic Methods for Toeplitz-like Matrices and Operators[M].Basel： Birkhauser，1984

[3] LANCASTER P，TISMENETSKY M.The Theory of Matrices with Applications[M].2nd New York： Academic Press，1985

[4] HELMKE U，FUHRMANN P A.Bezoutians[J].Linear Al-gebra and Its Applications，1989(122/123/124)：1039-1097

[5] GOVER J，BARNETT S.A Generalized Bezoutian Matrix[J].Linear and Multilinear Algebra，1990，27(11)：33-48

[6] MANI J，HARTWIG R E.Generalized Polynomial Bases and the Bezoutian[J].Linear Algebra and Its Applica-tions，1997，251(12)：293-320

[7] YANG Z H，HU Y J.A Generalized Bezoutian Matrix with Respect to a Polynomial Sequence of Interpolatory Type[J].IEEE Transactions on Automatic Control，2004，49(10)：1783-1789

[8] WU H Z.Generalized Polynomial Bezoutian with Respect to a Jacobson Chain Basis over an Arbitrary Field[J].Linear Algebra and Its Applications，2010，432：3351-3360

[9] BINI D A，GEMIGNANI L.Bernstein Bezoutian Matrices[J].Linear Algebra and Its Applications，2004，315：319-333

[10] WOLTERS H J，FARIN G E.Geometric Curve Approxi-mation[J].Computer Aided Geometric Design，1997，14(6)： 499-513

[11] WINKER J R.The Transformation of the Companion Matrix Resultant Between the Power and Bernstein Polynomial Bases[J].Applied Numerical Mathematics，2004，48： 113-126

[12] 郑婷婷，吴化璋.Bernstein Bezout矩阵与可控制型/可观测型矩阵之间的联系[J].重庆工商大学学报(自然科学版)，2017，34(2)：12-15

ZHENG T T，WU H Z.Connections between Bernstein Bezout Matrix and Generalized Controllability/observa-bility-type Matrices[J].Journal of Chongqing Technology and Business University (Natural Science Edition)，2017，34(2)：12-15