压缩式封隔器的密封胶筒材料性能研究

陆如东，钱 月

(1.上海优强石油科技有限公司，上海 201806；2.上海大学，机械自动化学院，上海 200072)

0 前言

封隔器胶筒所釆用材料是橡胶,其特点是当受到力很小时，就能产生较大的变形，即橡胶的超弹性。在大应变条件下,会出现应力加速增大、硬化或应力加速减小、软化的现象，具有几何非线性和材料非线性[1-2]。在进行有限元分析时，需要对橡胶材料的本构模型进行合理的选择，得到材料常数。2010年，陈健经胶筒模拟试验和现场试验，分析出胶筒的材料对密封性能的影响。实验结果表明，胶筒的综合性能会因热氧老化现象而降低，最终引起胶筒的密封失效[1]；2012年，于桂杰通过对添加了填料的橡胶进行单轴拉伸试验后，用Matlab拟合得到了Mooney-Rivlin模型和Yeoh模型的材料常数，并根据拟合数据曲线确定采用何种模型，最后利用ANSYS有限元模拟分析得到不同弹性模量的封隔器橡胶筒的坐封效果[4]；李鹏飞等以三胶筒封隔器胶筒为主要研究对象，探索了橡胶材料的应力和应变之间的关系[5]。

本文采用Yeoh应变能函数来描述其力学性能，对密封胶筒进行力学实验，根据实验所得到的应力应变数据，拟合应变能函数的材料常数[3]。

1 应变能密度函数

Yeoh应变能函数可以用来表达橡胶材料在大变形状态下的力学性能，适合作为封隔器密封胶筒的应力应变计算模。Yeoh应变能函数中的材料常数，可以通过单轴拉伸实验确定[6]。

应变能函数的表达式如下：

(1)

式中,I1,I2,I3为变形量张量的不变量；C为待确定的材料常数。其中

(2)

其中，λi为主伸长比。胶筒近似为不可压缩材料，则I3=1。方程(1)可以简化为

(3)

式(3)参数的Yeoh表达式为

W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3

(4)

Kirchhoff应力张量与Green应变张量之间的关系为

(5)

式中，tij、γij分别为Kirchhoff应力张量和Green应变张量。

根据应力张量与应变张量的关系，可得

(6)

由于采用单轴拉伸实验，则

(7)

联合方程式(6)、(7)及式(4)可得

(8)

(9)

将式(9)带入式(8)可得

(10)

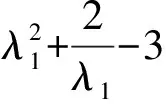
Y=2C10+4C20X+6C30X2

(11)

为了拟合力学常数C10,C20,C30需要对密封胶筒进行单轴拉伸实验以获取胶筒的应力和应变数值。

2 密封胶筒拉伸实验及材料常数拟合

2.1 密封胶筒单轴拉伸实验

对胶筒试样进行单轴拉伸实验，以获得封隔器密封胶筒的应力应变数据。实验过程中试样尺寸及所使用的剪裁、测量工具均参照国家标准GB/T 528-2009的要求[7]，选择便于打磨的II型哑铃状试样。试样尺寸如图1所示。

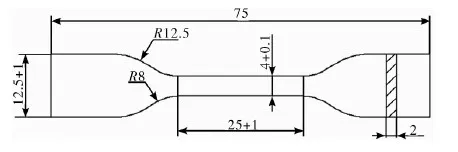
图1 哑铃型试样尺寸要求

采用符合GB/T2941要求的裁刀对封隔器密封胶筒进行剪裁，使用测厚计测量试样厚度。裁剪后的试样如图2所示。

图2 制样后的试样

实验仪器采用SCT-57(232)微机控制电子式万能试验机，见图3和图4。

图3 拉伸实验仪器

图4 拉伸实验

2.2 材料常数拟合

单轴拉伸实验共有边胶筒和中胶筒2个试样，每个试样测量2组数据，共4组数据。

在Origin中拟合Yeoh应变能函数中的材料常数。根据边胶筒测得的2组应力应变数据，拟合出的曲线如图5、6所示。

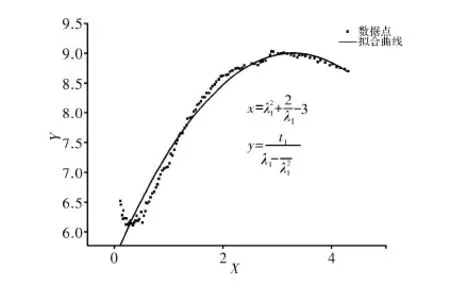
图5 边胶筒第1组数据的拟合曲线

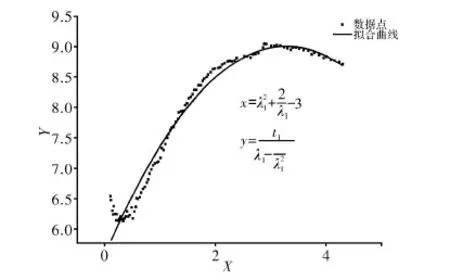
图6 边胶筒第2组数据的拟合曲线

边胶筒的拟合结果见表1、2。

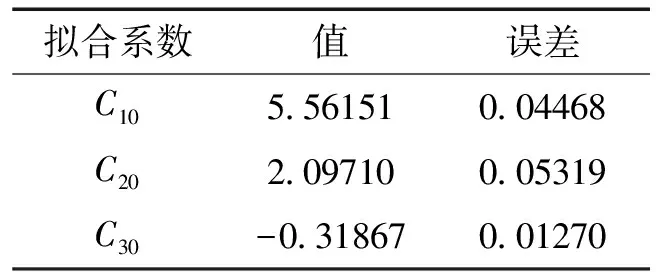
表1 边胶筒第1组数据对应的材料常数

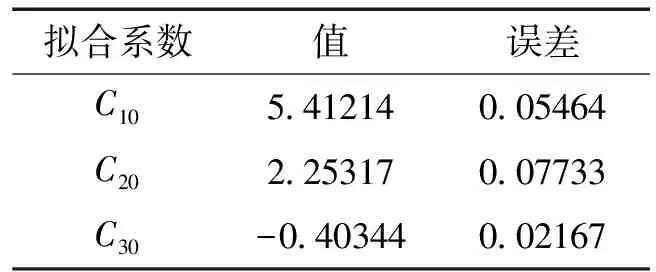
表2 边胶筒第2组数据对应的材料常数

对中胶筒进行相同的拉伸试验，得到两组应变数据，并在Origin中拟合Yeoh应变能函数中的材料常数，拟合出的曲线如图7、8所示。

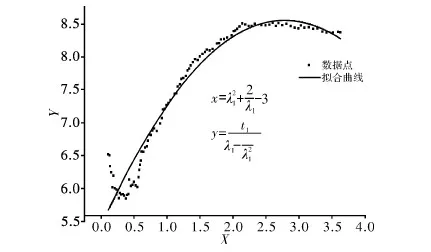
图7 中间胶筒第1组数据的拟合曲线

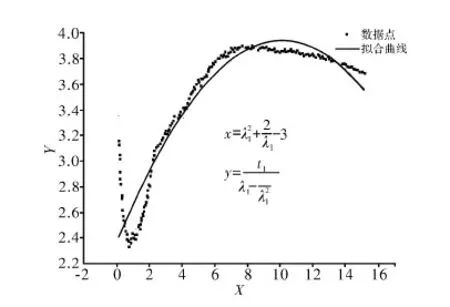
图8 中间胶筒第2组数据的拟合曲线

中间胶筒的拟合结果如表3、4。

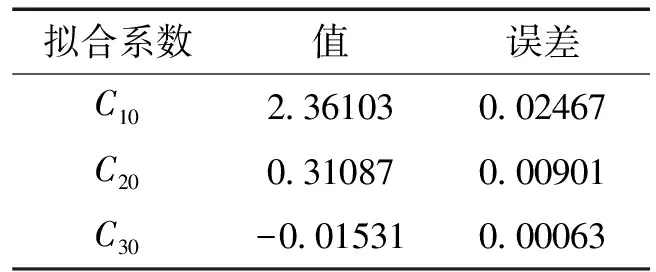
表3 中间胶筒第1组数据拟合结果

表4 中间胶筒第2组数据的拟合结果

从4组数据的曲线拟合结果可以看到，边胶筒对应的两条拟合曲线趋势基本相近，中间胶筒的两次拟合结果也大致相同。边胶筒的材料常数拟合中，第1组数据的拟合误差小于第2组数据的拟合误差，因此选取第1组数据的拟合结果作为边胶筒的材料常数。中间胶筒的材料常数拟合中，由于第1组数据的拟合误差小于第2组数据的拟合误差，因此选取中间胶筒第1组数据的拟合结果作为中间胶筒的材料常数。封隔器边胶筒和中间胶筒材料常数的最终拟合结果见表5。

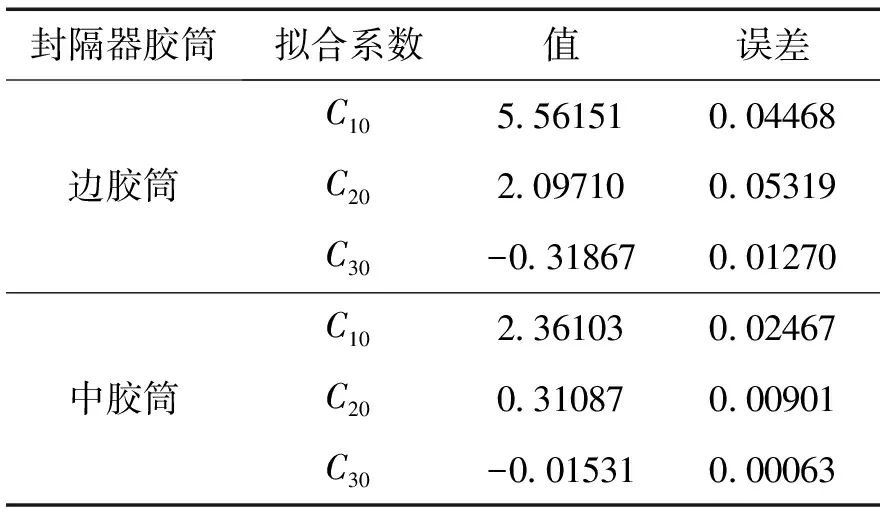
表5 封隔器边胶筒和中胶筒的材料常数拟合结果

3 结论

按照国家标准GB/T 528-2009对封隔器密封胶筒试样进行单轴拉伸实验，得到密封胶筒的应力应变数据。通过边胶筒和中胶筒的4组应力应变数据拟合，得出Yeoh函数中的材料常数，以便于封隔器密封性能的计算。

[1] 陈健，田播源，刘玉文，等.压缩式封隔器胶筒失效因素分析及措施[J].工业技术,2010,31(11):80-81.

[2] 仝少凯.压缩式封隔器胶筒力学性能分析[J].石油矿场机械,2012,41(12):1-7.

[3] 丁亮亮，练章华，彭建云，等.深层气井封隔器胶筒力学行为仿真[J].石油机械,2012,(09):92-95.

[4] 于桂杰，李长江，孙宝全，等.压缩式封隔器异型胶筒密封性能分析[J].润滑与密封,2015,40(01):45-46.

[5] 李鹏飞，刘旭辉，赵珩煜，等.三胶筒封隔器胶筒的密封性能分析[J].机械制造,2016,622(54):51-52.

[6] 张劲，李炜，张士诚，等.封隔器超弹性胶筒力学性能的试验研究[J].机械工程学报,2011,47(08):71-75.

[7] GB/T 528-2009,硫化橡胶或热塑性橡胶拉伸应力应变性能的测定[S].

[8] 张宝岭，王西录，徐兴平.高压封隔器密封胶筒的改进[J].石油矿场机械，2009,38(1).

[9] 陈庭根，管志川.钻井工程理论与技术[M].东营：石油大学出版社，2000.