轴流风机叶片优化设计仿真与模态分析

周 勃，王 慧，张亚楠

(1.沈阳工业大学 建筑与土木工程学院，辽宁 沈阳 110870；2.沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 前言

随着轴流风机在空调、冷却设备等机械制造业以及通风、散热等建筑业中的应用愈发广泛，风机噪声的影响日渐受到重视，而针对轴流风机叶片振动噪声控制方面的研究已成为当前气动声学领域研究的热点，在控制噪声的同时进行叶片参数优化进而提高轴流风机工作效率也是当前的研究重点。杨金军[1]通过建立叶片有限元模型进行模态分析，得到叶片的各阶固有频率及相应阵型，分析了可能产生共振的频率。瞿红春[2]等基于模态分析理论，运用实验设备和ANSYS软件对风机叶片进行有限元模态分析，计算其在不同转速下的固有频率和振型，分析发现了叶片最大变形量一般发生在叶尖或前缘处。张士伟等[3]针对轴流风机，利用流体分析软件Fluent对轴流风机进行了流场仿真分析和优化，研究了叶尖间隙对气动噪声的影响规律。叶学民等[4]通过ANSYS软件进行原叶片以及叶顶采用双凹槽结构叶片数值模拟，得到采用双凹槽叶顶结构后风机性能发生显著变化，设计工况下风机全压有所下降，同时效率有一定程度的提高。陈坤等[5]借鉴了雕鸮羽毛的消音机理，在轴流风机叶片上进行重构，设计了耦合仿生轴流风机，并通过试验优化的方法，得到了耦合仿生轴流风机具有较低的气动噪声值。Thompsom等[6]通过改变机壳形状实现梯状叶顶间隙结构，研究了九种不同的机壳结构，结果表明在小间隙和中等间隙下，梯状间隙结构可以有效提高风机的压比、效率和流量范围。Ameri等[7]研究了平叶顶及两种不同深度的凹槽状叶顶对风机工作效率的影响。由于轴流风机在运转时，会不断受到脉动气流的作用，使叶片产生振动，当激振力频率等于叶片自振频率而产生共振时，会使叶片疲劳断裂，而风机叶片损坏的原因，多是由于叶片振动疲劳所引起。因此，对轴流风机叶片做模态分析研究是非常重要的。

综上所述，学者们对于轴流风机叶片表面结构参数优化的研究还比较少，特别是没有把对叶片进行模态分析和叶片表面结构参数优化设计有效地结合起来，尤其是对于避免在轴流风机运作过程中产生共振和通过叶片表面的优化设计来提高轴流风机工作效率两者统一考虑的研究很少。

鉴于此，本文基于模态分析理论和计算流体力学进行数值模拟仿真和模态分析，结合模态分析对轴流风机叶片表面结构进行参数化设计并得出最优设计，使轴流风机在该设计下工作效率有一定的提高。

1 模态分析理论基础

实际的机械结构在计算的过程中常常会被简化成多自由度的系统，该系统可以写成如下的耦合方程形式，可以用矩阵来表示如下[8]：

(1)

式中，X为系统每个自由度的位移向量，对应着系统的各个自由度；M为系统的质量矩阵；C为系统的阻尼阵；K为系统的刚度矩阵；F(t)为系统所受的外力。

为了求解的方便，假设为无阻尼的情况(C=0)，

(2)

通过求解可以得到的表达式{X}的表达式为

(3)

令

{Ψr}T[M]{Ψr}=mr

{Ψr}T[K]{Ψr}=kr

式中，mr、kr分别为r阶振动模态的等效质量和刚度，称为模态质量和模态刚度。

所以有ω2=kr/mr，故有

(4)

式(4)左边X为机械结构上各点的振动情况，右边表示各个振动模态的mr、kr、ωr以及{Ψr}的组合，这就是模态叠加原理，是模态分析的理论基础。mr，kr，ωr称为模态参数。

2 计算流体力学基本控制方程

控制方程是物理学守恒定律的数学表达形式，流体在流动过程中要遵守质量守恒定律和动量守恒定律等基本守恒定律。

2.1 质量守恒方程

流体流动质量守恒是流体介质流过空间某一控制体V，在相同的时间内，控制体内的质量变化率等于穿过控制体表面S的质量流量。其积分形式表示为

(5)

经过化简式(5)变为

(6)

此方程也称为连续方程，引入散度表达方式，可表示为

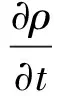
(7)

式中，ρ为流体密度；n为单位法向向量；t为流体流动时间；U为流体速度矢量；u、v和w为U在x、y和z方向上的分量。

风力机叶片流场仿真过程中，将空气视为不可压缩气体，密度ρ为常数，那么式(6)则变为

(8)

2.2 动量守恒方程

动量守恒是从牛顿第二定律发展过来的，可以表述为：控制体中流体的动量对时间的变化率等于外界作用在控制体上的各种力之和。在x、y和z三个方向的动量守恒方程可表示为

(9)

式中，p为流体控制体上的压力；τxx、τxy和τxz等为控制体表面上粘性应力τ的分量；Fx、Fy和Fz为控制体上的体力。

3 轴流风机叶片优化设计与模态分析

3.1 原型风机

选取德通JGFS5-4型轴流风机为原型对其叶片进行优化设计，原型风机主要参数如下：转速1 420 r/min，全压为196 Pa，电压为380 V，流量为9 300 m3/h，功率为3 kW。设计叶轮外径为500 mm，轮毂比为0.4，叶片采用圆弧等厚板叶形，厚度为4 mm,叶片叶根处安装角为40°，叶顶处为35°。

3.2 叶片优化设计

现如今的轴流风机叶片仍然是叶面光滑形态，由于存在叶顶泄流导致叶顶间隙涡流的出现，从而影响风机的工作性能，因此本文对叶片表面进行两种形态参数化优化设计，以减少轴流风机工作过程中经由叶片表面流向叶顶间隙的气流，从而降低叶顶涡流的作用，达到提高风机工作效率的目的。

优化叶片为在原风机等厚叶片表面布置三棱柱体以及半圆柱体，在风机叶片表面沿逆螺旋展开，螺旋柱体由叶片顶部过渡到叶片根部。原型风机叶片厚度为4 mm,三棱柱体截面采用等边三角形，相邻三棱柱体间距为22 mm，高度为叶片厚度a的20%；相邻半圆柱体间距为22 mm，截面采用半径为叶片厚度b的20%，如图1所示。

图1 风机叶片截面图

通过计算流体力学数值模拟仿真，对比分析采用优化叶片的轴流风机与原型叶片风机工作状态，在额定转速下由CFD计算得到三种不同情况的流量-静压曲线如图2所示。

图2 三种风机叶片流量-静压曲线

比较三种风机的模拟流量-静压曲线可以明显发现，三棱柱体和半圆柱体优化风机的气动性能好于原型风机，三棱柱优化风机效果更为显著，最大流量提升了5.8%，最大静压提升了7.3%。分析原因可能是逆螺旋状的柱体叶片表面能够阻碍气流沿径向扩散，减少了进入叶顶间隙的气流，所起的导流作用使更多的气流靠近轴心流出，从而使出口流量和压力都增大。

3.3 模态分析

3.3.1 有限元模型的建立

对于JGFS5-4型风机叶片，选用的材质为压铸铝合金，具有良好的耐蚀性和抗氧化性，密度小而刚度大，其参数性能如表1所示。

表1 叶片材料参数

本文采用Solidworks建模软件进行三种不同类型的风机叶片建模，并导入ANSYS软件中。叶片有限元单元类型选用Solid95单元，具有塑性、蠕变、应力刚度、大变形和大应变能力。网格采用自由划分，其中表面采用三棱柱逆螺旋布置的叶片模型网格划分图如图3所示。

图3 三棱柱表面优化叶片网格划分图

3.3.2 叶片固有频率的计算

约束叶片在x、y、z三个方向上的位移，选用BlockLanczos为求解方法，设置求解频率范围为0～2 200 Hz，计算三种不同类型叶片的固有频率，结果如图4～6所示。

图4 原型风机叶片模态振型图

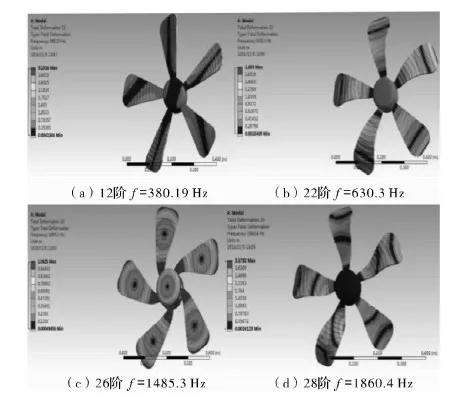
图5 三棱柱逆螺旋表面风机叶片模态振型图

图6 半圆柱逆螺旋表面风机叶片模态振型图

由模态振型图可以看出，三棱柱体和半圆柱体的优化风机叶片较原型风机叶片的固有频率有一定的提高，而通过差值比较，三棱柱体的优化效果更优，其叶片固有频率提升了2.3%。固有频率的提升，能够有效延缓由激振频率和固有频率共同作用而引起的共振的产生，因此对于提高风机工作性能以及降低工作噪声有显著效果。

4 结束语

(1)通过对原型风机叶片两种不同表面形态优化设计的模拟分析，得到其额定转速下流量-静压曲线，比较分析曲线可知，三棱柱体表面优化叶片后的风机工作性能有所提高，最大流量提升了5.8%，最大静压提升了7.3%。

(2)建立三种风机叶片有限元模型并进行模态分析得到，三棱柱体和半圆柱体表面优化叶片其固有频率升高2.3%，这样能有效延缓共振的发生，改善了风机的工作性能。

[1] 杨金军.基于ANSYS的轴流风机叶片模态分析[J].风机技术，2014(Z1):37-39.

[2] 瞿红春，黄远强，王涛，等.民用发动机风扇叶片模态及共振分析[J].中国民航大学学报，2015，33(06)：14-16.

[3] 张士伟，陈长征，周勃.装载机轴流风扇的气动声学性能优化与分析[J].重型机械，2015，(05)：59-62.

[4] 叶学民，李鹏敏，刘春曦.双凹槽叶顶结构下的轴流风机性能及叶片振动特性研究[J].机械工程学报，2015，4(51)：167-174.

[5] 陈坤，刘庆平，廖庚华，等.利用雕鸮羽毛的消音特性降低小型轴流风机的气动噪声[J].吉林大学学报，2012(42)：79-84.

[6] THOMPSON D W,KING P I,ROBE D C.Experimental investigation of stepped tip gap effects on the performance of a transonic axial-flow compressor rotor[J].Journal of Turbomachinery,1998,120(03)：477-486.

[7] AMERI A A,STEINTHORSSON E,RIGBY D L.Effect of squealer tip on rotor heat transfer and efficiency[J].Transactions-American Society of Mechanical Engineers Journal of Turbomachinery,1998,120(04)：753-759.

[8] 成德，薛亚波，樊启泰.风机模态分析理论基础与实验研究[J].风机技术，2012(06):11-21.