“信号与系统”教学引入图像处理案例探析

吴宪祥， 郭宝龙， 朱娟娟， 张玲霞

(西安电子科技大学 空间科学与技术学院 ICIE研究所， 陕西 西安 710071)

0 引言

“信号与系统”是通信、信息、电子、自动化、电气等专业本科生的一门核心专业基础课程，它是学习“通信原理”、“数字信号处理”、“电磁场”、“自动控制原理”等后续课程的基础，也是相关专业研究生入学考试的一门重点课程。该课程的主要特点是数学概念抽象、理论性和逻辑性强、工程应用背景突出，因此导致该课程难教、难学[1-3]。

数字图像处理是数字信号处理的一个重要分支，其很多技术源自信号与系统相关理论。由于数字图像处理的输入和输出都是图像，非常直观，有利于加深学生对“信号与系统”课程中复杂概念的理解[4]。在“信号与系统”教学过程中，我们将若干典型的数字图像处理工程案例应用于教学演示，以此激发学生的学习兴趣，培养学生的工程意识，提升课堂教学效果。

1 图像配准中的相位相关法

Kuglin等人在1975年提出了相位相关法，借助傅里叶变换将两幅待配准的图像变换到频域，根据傅里叶变换的移位性质，利用互功率谱直接计算出两幅图像间的平移量[5]。相位相关法基本原理如下[6]：

设图像I1(x,y) 和I2(x,y)之间存在平移量(Δx,Δx)，其中

I1(x,y)=I2(x-Δx,y-Δy)

(1)

由傅里叶变换的移位特性，有

(2)

其归一化的互功率谱为

(3)

互功率谱的相位等于两幅图像的相位差。归一化的互功率谱进行逆傅里叶变换，得到一个冲激函数

Corr(x,y)=F-1[e-j2π(uΔx+vΔy)]=δ(x-Δx,y-Δy)

(4)

该函数在两幅图像的相对位移(Δx,Δy)即“匹配点”处取最大值，其它地方接近零。找出式(4)中的峰值点对应的位置，就可以确定平移量：

(5)

在图像之间仅存在平移的情况下，冲激函数峰值的大小反映了两幅图像之间的相关性，在[0,1]区间取值。两幅图像重叠区域越大，其值越大。如果两幅图像内容相同时，其值为1；完全不同时，其值接近0。

图1(a)和图1(b)是仅存在水平和垂直方向平移关系的两幅图像，图1(a)大小为273×191，图1(b)大小为201×264，图1(c)为利用本文改进的相位相关法检测到的δ函数，峰值为0.3365，根据文献[6]改进的相位相关法估计出平移量为(-104,-99)。如果两幅待配准图像间还存在旋转和尺度关系，可以先采用对数极坐标傅里叶变换并利用相位相关法进行旋转和尺度参数估计后再进行平移参数估计[7]。

通过这个工程案例的学习，学生对傅里叶变换的性质、互功率谱、冲激函数等概念具有更加深入的了解，该过程激发了学生对信号与系统课程深入学习的兴趣。

(a) 图像序列1 (b) 图像序列2

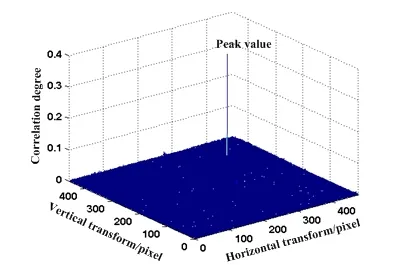
(c) 由(a)和(b)检测到的 函数

2 “玛丽莲·爱因斯坦”图像合成

2.1 案例引入

2007年，美国麻省理工学院的神经科学家奥迪·奥利瓦、安东尼奥·托拉尔巴和英国格拉斯哥大学的研究人员菲利皮·斯奇恩斯利用人类大脑对清晰和模糊画面的反应差异，提出了著名的“玛丽莲·爱因斯坦”图象合成，如图2所示[8]。当近距离看时，能清楚地认出画中人是20世纪著名科学家阿尔伯特·爱因斯坦；但远距离看时，画中人神奇地变成了美国好莱坞已故影星玛丽莲·梦露！

图2 玛丽莲·爱因斯坦

2.2 案例分析

为什么会产生这种效果呢？其实，这幅画由爱因斯坦头像的高频分量(图像灰度变换剧烈的部分，即边缘和细节)和玛丽莲·梦露的低频分量(图像灰度变换平缓的部分，即整体轮廓)合成[9]，如图3所示。利用基本的傅里叶分析可以方便地完成类似的合成图像。

定义:高斯滤波器(方差σ，均值(a,b))

低通：H(u,v)=exp{[(u-a)2+(v-b)2]/2σ2}

(6)

高通：H(u,v)=1-exp{[(u-a)2+(v-b)2]/2σ2}

(7)

图3 玛丽莲·爱因斯坦合成示意图

有趣的是，如果将爱因斯坦头像的低频分量和玛丽莲·梦露图像的高频分量合成，得到的图像颇具喜感，如图4所示。

图4 阿尔伯特·梦露合成示意图

通过这个工程案例的学习，学生即使不了解算法的具体实现方法，也可以直观地看出低通/高通滤波效果，明白了低频分量对应的是图像的整体轮廓和主要信息，高频分量对应图像的边缘和细节，同时，对频率域信号分析的优越性有了深刻的体会。

3 结语

变换域分析是“信号与系统”课程的精髓，也具有广阔的工程应用背景。频域分析抽象，需要很强的数学分析能力和变换域思维，是“信号与系统”课程教学的重点和难点之一。本文将数字图像处理的典型工程案例引入“信号与系统”课程教学，提高了内容的直观性，促进了理论回归工程，开拓了学生的学习思路，活跃了课堂气氛，提高了课堂教学效率，使学生深刻理解到“信号与系统”课程内容的重要性和工程意义。

[1] 郑君里，谷源涛． 信号与系统课程历史变革与进展[J]，南京: 电气电子教学学报，2012，34(2): 1-6．

[2] 吴宪祥，郭宝龙等. “信号与系统”课程交互式教学体系构建[J]. 南京: 电气电子教学学报，2015，37(1)：26-28.

[3] 李建华，马晓红，邱天爽．“信号与系统”课程体系剖析[J]，南京:电气电子教学学报，2010，32(2): 14 -16．

[4] 诸葛霞，袁红星，孔中华等. 信号与系统课程中数字图像处理教学案例研究[J].宁波: 宁波工程学院学报, 2014, 26(4): 79-82.

[5] C. Kuglin, D. Hines. The phase correlation image alignment method. Conference on Cybernetics and Society[C]. New York: IEEE, 1975:163-165.

[6] 吴宪祥, 郭宝龙, 王娟.一种改进的序列图像自动排序算法[J]. 天津: 光电子-激光, 2009, 20(8): 1114-1117.

[7] LIU Han-zhou, GUO Bao-long, FENG Zong-zhe. Pesudo-log-polar Fourier Transform for Image Registration[J]. New York: IEEE Signal Processing Letters, 2006, 13(1): 17-20.

[8] http://cvcl.mit.edu/hybrid_gallery/gallery.html[EB/OL].

[9] https://jeremykun.com/tag/marilyn-monroe/ [EB/OL].