无损线终端接任意负载暂态响应分析
齐 超, 徐汉卿, 黄奕毅, 吴 婷
(哈尔滨工业大学 电气学院, 黑龙江 哈尔滨 150001)
0 引言
近年来,随着电力系统传输距离的不断增加,规模的不断扩大及超大集成电路的快速发展,传输线暂态响应的研究受到越来越多的关注。从传输线方程入手,利用数学工具和计算机技术,已有文献采用数值求解方法分析了传输线暂态问题[1-2],但在如何求取解析解方面研究较少。文献[3][4]提出了一种运用卷积定理较为系统的复频域分析法来获得无畸变传输线的暂态响应,但是文中所提的递推方法求解最终响应,较为复杂繁琐。
在“电路理论基础”均匀传输线学习中可知,行波可以很好地描述阶跃电源在均匀线上的传输过程。当无损线始端接通激励源后,电压/电流正向行波均由始端向终端推进。当正向行波传播到负载端、两不同线路的接头处、线路的分支处或接有集中参数元件处等,都会产生波的反射。书中讨论了均匀线终端开路、短路、匹配及一阶RC(或RL)等一般性负载情况[5]。对于行波在第一次传输到负载时,用彼得生法则结合三要素方法能够较好地分析终端负载电压电流解析解。然而,这也只能求解行波第一次到终端时的情况,对于后面的多次传输反射的情形却无法处理。另外,三要素法更多只适用于负载仅有一个电容或电感。对于含有多个动态元件情形,彼得生法则在分析阶跃电源的暂态过程上具有较大的局限性。
本文对无损均匀线暂态响应进行研究,提出了基于“附加电源”求解每一时间段终端暂态响应的通用新方法,为分析复杂负载情况下均匀线传输过程提供了理论依据和实验验证。
1 均匀传输线
1.1 传输线方程及其解
均匀传输线作为分布参数电路,各处电压与电流均是关于时间和位置的函数,其偏微分方程表达式如下[5]:


(1)
式中,R0、L0分别为单位长度均匀线(往返)上电阻 (SI单位:Ω/m)、电感(SI单位:H/m);G0、C0分别为单位长度两线间电导 (SI单位:S/m)、电容 (SI单位:F/m)。对于一定的均匀线,它们都是常量,但R0和G0并非互为倒量。
对于无损均匀线,R0=0、G0=0,根据拉普拉斯变换的线性性质和微分性质,式(1)表达为


(2)
这是一组关于x的常微分方程,其通解为


(3)

根据拉普拉斯反变换的线性性质和延迟性质,对应沿线电压、电流时域解为
u(x,t)=u′(t-x/v)ε(t-x/v)+u″(t+x/v)ε(t+x/v)=u+(x,t)+u-(x,t)

(4)
式中ε(·)是单位阶跃函数。可见,均匀传输两线间的电压等于正向和反向行波电压之和,电流等于正向与反向行波电流之差。
1.2 行波的多次反射
电压、电流在均匀传输线上是以速度不变的行波方式传播的,当无损均匀线终端和始端都不匹配时,两端都要产生反射波,形成多次反射。设图1中无损线为零初始状态,其波阻抗为Zc,线长为l。

图1 终端和起端都不匹配的无损均匀线
始端接电源电压uS=USε(t)、内阻Rs≠Zc,终端负载阻抗ZL≠Zc。设始端反射系数N1与终端反射系数N2分别为
(5)
图2示意了此传输线中电压行波多次反射的过程

图2 传输线电压行波多次反射示意图
由此可见,当
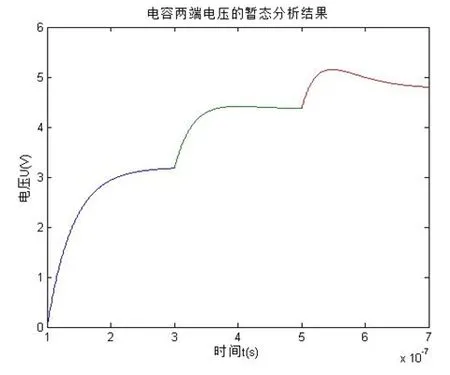
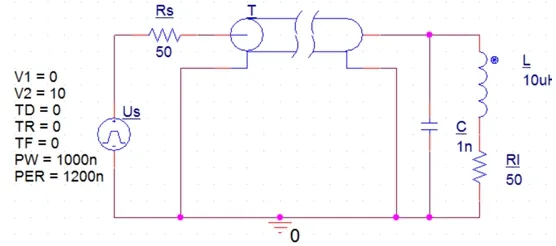
(2k+1)td 时,终端电压表达式 (6) 式中U+是始端入射电压,表达式为 图1所示为终端和始端都不匹配的无损均匀线,设激励电源为阶跃电源uS=10ε(t) V。内阻RS为50 Ω。无损均匀传输线波阻抗Zc为200 Ω,电流从一端传到另一端的传输时间为0.1 μs。负载电容C为1 nF。电阻RL为50 Ω。下面分析电容两端电压uC随时间t的变化情况。 由于电容的u-i关系是非线性的,不能直接应用行波传输公式。因此对电路中所有元件进行拉式变换使其转为线性,对应复频域下电源、源内阻、波阻抗、电容、负载电阻的计算值分别为10/s、50、200、109/s、50。具体分析过程如下: (1) 当时间为[0 μs,0,1 μs]时,行波还没有传输到电容上,因此uc为0不变。 (3) 当时间在[0.3 μs,0.5 μs]时,行波将第二次传到电容上。对于左侧的电源US来说,它对这一过程的贡献也以行波发生反射表达,反射系数为N1。所以此时电容两端的电压为U21=(1+N2)(1+N1N2)U+。 以后乃至更多时间段的行波传输都是类似的,但是需要引起注意的是,由于电容在每段传输对应的电压初值都不同,所以其在拉氏变换下等效出的计算电压值也不同。也就是说,每隔0.2 μs就要更换“附加电源”,因此每一传输时段内附加电源产生的行波只有一次。沿线任意处电压、电流响应是由始端激励源的贡献和电容附加电源一次作用的合成。 对图1所示终端和始端都不匹配的无损均匀线Matlab理论分析计算结果如图3所示。 由图3可见,在[0 μs,0.1 μs]时段,电容电压为零状态响应,表达式为u(t)=A(1-e-t/τ),A为一确定的常数,图像为指数形状。uC以速率减小的方式不断增大并趋于稳定。 图3 负载电压理论计算结果 在[0 .1μs,0.3 μs]时段,激励电压源US的行波再次传输过来,破坏了第一时段的稳定状态。由于电容电压具有连续的特点,因此后一段的起点与前一段的终点在0.3 μs处重合,并继续开始充电。这时电容两端电压有两个来源,一个为始端激励源US,其产生的响应分量还是零状态,以速率减小的方式增长并趋于稳定,表达式为u1(t)=B(1-e-(t-t0)/τ);另一个为“附加电源”,其产生的响应为零输入过程,响应分量以速率不断减小的方式变化,同样趋于稳定,表达式为u2(t)=Ce-t/τ,B、C均为确定常数。前者响应不断增大,后者响应不断减小,其合成响应为先增大,达到区段极值后减小,最后趋于稳定。以后乃至更多时间段的传输过程都是类似重复,在此不再赘述。 用ORCAD进行电路仿真,其模型如图4所示,实验结果如图5所示。 对比图3可见,理论计算的uC(t)与仿真实验结果形状、数值等都吻合得很好,当时间趋于无穷时,两个图像的电压最终都趋于5 V。这相当于将传输线等效为集中参数理想导线时的结果,也再次验证了文中提到的观点:在阶跃激励下,电容储能并激发出了“附加电源”,不同时段上的,“附加电源”的一次行波和始端激励源的行波作用共同影响了终端负载的电压。 将负载再加上一个电感线圈,大小为10 μH,仿真电路如图6所示。 图4 RC负载的仿真电路 图5 仿真结果 图6 RLC负载电路图 由于引入了同样具有储能本领的电感,第二次行波传输以及后面的传输,负载区相当于两个“附加电源”,我们每计算一时间段传输过程,都需要以前一段暂态分析的电容电压uC和电感电流iL作为基础。 图7和图8分别为Matlab下理论计算和在ORCAD下实验仿真的电容电压随时间变化结果。 可见两个曲线吻合很好,再次验证了本文提出的储能元件具有“附加电源”功能,此分析方法具有通用性,即适用于任意线性负载。 本文对均匀传输线终端接任意负载时的传统解析求解提出了一种新思路,即用“附加电源”计算负载内部储能元件产生的响应分量。利用拉普拉斯变换使电源、负载等电路元件在复频域下都具有线性性质,从而转化为线性电路分析。(齐 超等文) 图7 RLC负载电路理论计算结果 图8 RLC负载电路仿真实验结果 然后在线性条件下利用行波方程解及分析多次反射的相关原理,分时段求解电源和负载内储能元件产生的响应分量,最后应用叠加定理得到总响应。利用拉普拉斯反变换代替传统的时域卷积法,进一步优化了求解过程。最终通过仿真验证了这种新思路的正确性。 本文通过对传输过程进行分段研究,最后得到了精确的解析解,为传输线的设计、分析提供了理论依据,具有一定的现实指导作用。 [1] J A Roden, C R Paul, W T Smith. Finite difference time domain analysis of lossy transmission lines [J]. IEEE Trans. On Electromagnetic Compatibility, 1996, 38(1): 15-24. [2] 卢斌先,王泽忠,程养春. 基于拉氏反变换的传输线耦合电流半解析解[J]. 北京:电网技术, 2007,31 (14):52-56. [3] 孙韬,侯世英,伍小兵.一种计算无损传输线上电压电流解析解的方法. [J]. 南京:电气电子教学学报, 2008,30 (3):20-22. [4] 孙韬, 侯世英. 无畸变传输线接电感负载时的波过程及算法分析[J]. 广州:电路与系统学报,2011,16 (1):47-51. [5] 孙立山,陈希有.电路理论基础(第四版)[M]. 北京:高等教育出版社, 2016,3: 366-372.2 电路模型与仿真分析
2.1 RC负载模拟电路分析

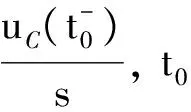

2.2 RC负载仿真分析
2.3 RLC负载电路分析与仿真


3 结语



