应用语言学研究中的图示与稳健统计方法
鲍 贵
(南京工业大学 外国语言文学学院,江苏 南京 211816)
0 引言
在研究数据满足统计假设(statistical assumptions)的情况下,常规(standard;conventional)统计分析方法(如方差分析)是恰当的选择。但是,如果研究数据违反了统计假设,使用常规统计方法就会影响统计效力,得出误导性甚至错误的结论。譬如,Wilcox(1998)发现,在正态分布时,如果两个总体平均数分别为0和1,方差均为1,使用t检验(n= 25,α= .05)的统计效力为0.96,但是如果两个总体是污染的正态分布(重尾巴,轻度违反正态分布),统计效力只有0.28。因此,探索数据模式,尤其诊断统计假设,是严谨的统计分析不可或缺的。但是,应用语言学研究者忽视统计假设的现象相当普遍(Plonsky,2014;Larson-Hall et al.,2015;鲍贵,2012)。究其原因,一方面可能是因为研究者对统计假设认识不足,没有掌握有效的统计假设诊断或检验方法;另一方面可能是因为研究者不知道如何应对统计假设违背的情形。实际上,统计学研究在数据分析方面的两大进展已为研究者提供了有价值的统计分析技术。一是图示方法(graphical methods),二是稳健(robust)统计方法。图示方法是视觉化的探索式数据分析技术(包括统计假设的诊断),常常能够揭示推理统计不易发现的数据特点和模式。稳健统计方法是现代统计技术。在统计假设满足的情况下,稳健统计方法与常规统计方法不相上下,但是在统计假设违反的情况下,稳健统计方法有着明显的优势,不受或较少地受到违反统计假设对统计分析结果造成的不利影响。
在应用语言学界,除了为数不多的教材介绍图示方法(Johnson,2008;Gries,2013)和稳健统计方法(Larson-Hall,2016)之外,学术期刊论文很少介绍或使用这些方法(Larson-Hall et al.,2010;Larson-Hall,2012;Plonsky et al.,2015;鲍贵,2016;2017)。鉴于应用语言学研究在进行组间比较时很少使用统计学家大力推荐的箱图(boxplot)(Larson-Hall et al.,2010),本研究拟介绍箱图的构造原理。更为重要的是,任何图形,包括箱图在内,都有不足之处,因而多图诊断更值得推介。另外,前期应用语言学文献未能将图形诊断与稳健统计方法的选择有机地结合在一起。本文克服这些局限,介绍箱图、核密度图和LOWESS(locally-weighted scatterplot smoother,局部加权散点图平滑方法)以及稳健方差和协方差分析(即选点分析,pick-a-point analysis)的原理,以真实数据为例探讨这些方法的应用。本文使用的统计软件为R 3.4.0,稳健统计分析使用的函数来自Wilcox(2017)*稳健统计分析数据包为Rallfun-v34。。
1 箱图与核密度图
1.1箱图
箱图是由Tukey(1977)创建的图示方法。它利用箱体和触须(whisker)概括数据的重要信息,因而又称箱-须图(box-and-whisker plot)。传统上,箱体概括的数据信息简称五数总括(five-number summary),即最小值(minimum,Min)、下枢(lower hinge,HL)、第2个四分位数(second quartile,Q2,常称作中位数M)、上枢(upper hinge,HU)和最大值(maximum,Max)。最小值和最大值提供数据分布尾巴的信息。中位数反映分布的中心。上、下枢距离反映分布的展度(spread);利用上、下枢构建的上、下围(upper fence,FU;lower fence,FL)用于诊断异常值(outlier)。中位数以及上、下枢的位置反映数据分布的偏度。换言之,五数概括涵盖变量的四个主要特征:中心、展度、非对称性(asymmetry)和异常值(Hintze et al.,1998:181)。箱图的基本构造如图1所示。
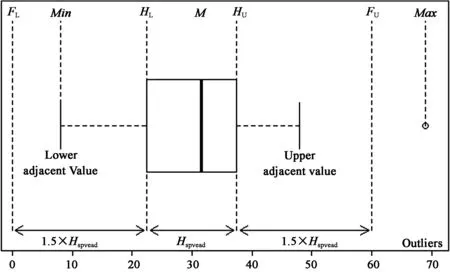
图1箱图构造
图1是水平放置的箱图。长方形箱体的两条边由上、下枢确定,分割箱体的粗线段代表中位数。上枢为大于中位数的一半数据的中位数,即上四分(the upper fourth);下枢为小于中位数的一半数据的中位数,即下四分(the lower fourth)。R默认的上、下枢采用这一定义。也有箱图采用上、下四分位数(the upper quartile,Q3;lower quartile,Q1)表示上、下枢(Wilcox, 2012;Kabacoff,2015)。上、下四分与上、下四分位数接近,但是由于算法不同,它们之间有时会有小的差异。关于分位数的算法,可参考Hyndman et al.(1996)和Ugarte et al.(2015)。图1中位数线代表的值是31.5。上、下枢各为37.5和22.5。枢展度(Hspread)为15。枢展度又称四分展度(fourth-spread),近似于四分位距(interquartile range,IQR),囊括了50%的中间数值。图1中的上围和下围反映异常值的临界值(outlier cutoff)。计算上,FU=HU+1.5×Hspread,FL=HL-1.5×Hspread。在标准正态分布时,上、下围包括了约99.3%的数据,只有0.7%的数据位于上、下围之外,被判定为异常值。利用上、下围定义异常值有些武断,但是经验表明,这个定义能够很好地识别可能需要给予特别注意的数值(Emerson & Strenio,1983:62)。在图1中,FU= 60,FL= 0。有一个用圆圈表示的异常值位于上、下围之外。由上、下枢向外垂直延伸的虚线称作触须。上邻近值(upper adjacent value)表示在上围内的最大数值;下邻近值(lower adjacent value)表示在下围内的最小数值。图1表明,数据分布不够对称,下须线比上须线略长,但是异常值使右尾巴变长。
尽管传统箱图是非常有价值的图形诊断方法,但是它不能诊断数据分布的峰态(如多峰态,multi-modality)和提供其他统计信息(如平均数)。克服传统箱图的局限有两种方法。一种是对传统箱图进行改造,比如添加平均数或绘制小提琴图(violin plot)(McGill et al.,1978)。另外一种方法是多图并用,彼此取长补短。
1.2核密度图
核密度图不仅能够直观地显示分布尾巴,而且还能够显示分布的峰顶(peak)、肩部(shoulder)和凸块(bump,数据的聚合),是对传统箱图的很好补充。
核密度估计是估计连续性随机变量概率密度函数的非参数方法,目的是依据样本估计一个真实的未知概率密度函数。核密度估计的函数是:
公式中,K(·)是核密度函数,h是平滑参数,又称带宽(bandwidth),n是样本量(Ugarte et al., 2015:115)。
常用的核密度函数有高斯(正态)函数、矩形(均匀)函数和三角函数等。这些核密度函数的特点是单峰(unimodal)、围绕0点对称和曲线下的单位面积为1(Keen,2010:161)。R默认的核密度估计函数是高斯核密度函数。
核密度估计中,选择适合的带宽非常重要。带宽过窄时,核密度估计偏差小,但是方差大;带宽过宽时,核密度估计方差小,但是偏差大(Keen,2010:167)。视觉上,带宽过窄导致密度估计曲线过于起伏,使分布模式难以察觉;带宽过宽导致曲线过于平滑,给分布形状的判断带来错觉。R默认的带宽计算上采用Silverman经验法则(Silverman,1986:47-48):h= 0.9An-1/5,其中,A= min(SD,IQR/1.34),即A取标准差(SD)和四分位距除以1.34的商之间的较小值。
图2是反映上节数据分布形状的高斯核密度图。在水平轴上的轴须图(rug plot)中,轴须代表样本数据值(n= 20)。采用的带宽为R默认算法计算出的值(h= 5.35)。
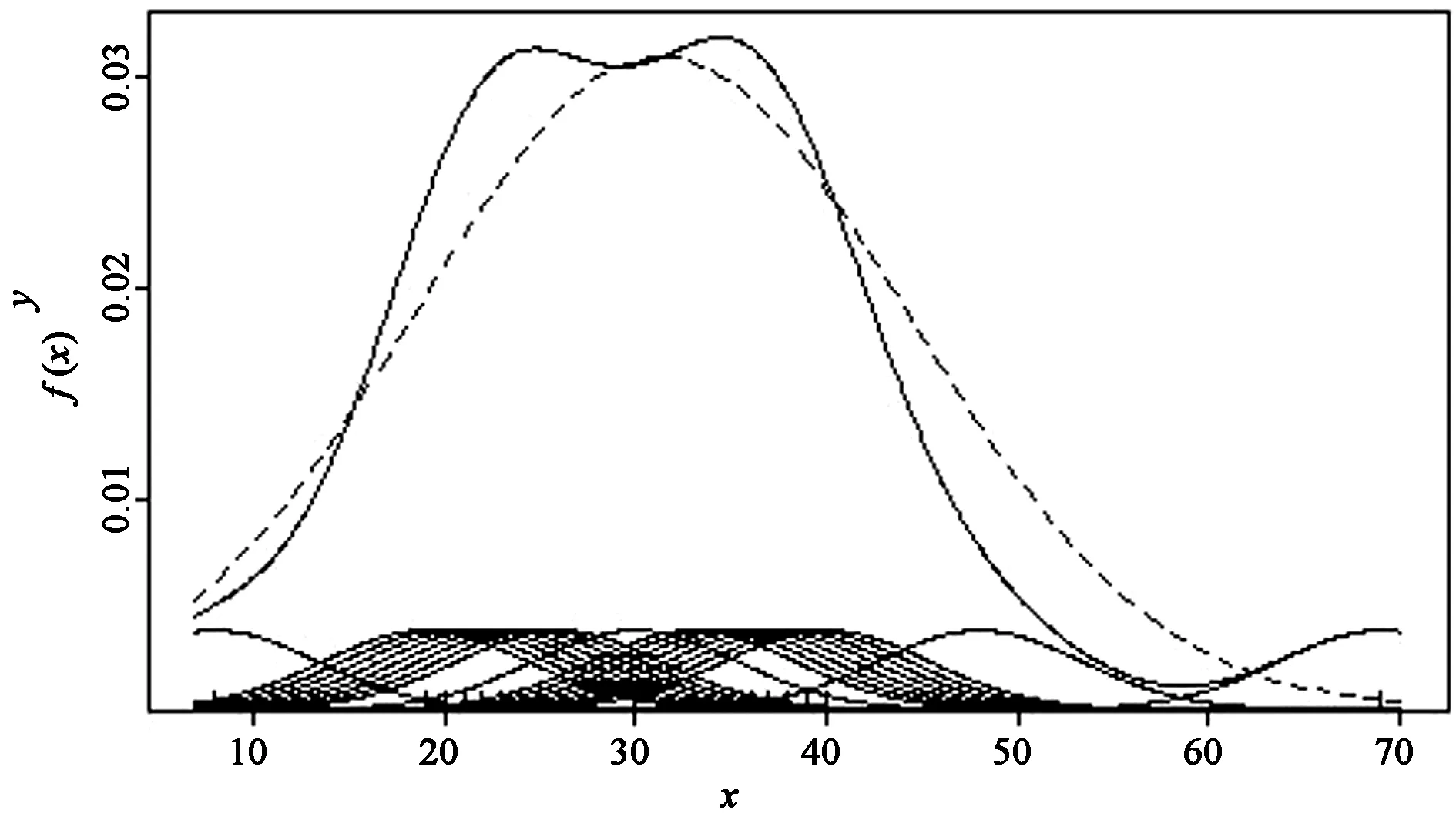
图2 核密度估计
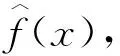
1.3 箱图与核密度图应用
在应用语言学研究中,箱图与核密度图可用于直观地比较不同组数据分布的基本特点。本节利用Ellis et al.(2004)研究中的部分数据介绍箱图和核密度图的实际应用*本节以及第3、4节数据均来自http:∥cw.routledge.com/textbooks/9780805861853/spss-data-sets.asp.。
Ellis et al.(2004)设计无准备(no planning,NP)、任务前准备(pretask planning,PTP)和在线准备(on-line planning,OLP)三个条件调查对42名中国英语学习者记叙文写作质量多个测量指标的影响。本例选择的测量指标是非流利度(dysfluencies)。该设计为被试间均衡设计(n1=n2=n3= 14)。
Ellis et al.(2004)没有在研究中报告各个条件数据分布的具体特点,采用常规的单因素方差分析和Scheffé配对比较方法检验准备条件对学习者非流利度的影响。本节主要诊断数据分布的特点,判断这些统计检验方法是否合适。
1.3.1箱图诊断
利用本例数据,图3比较三个准备条件组非流利度数据分布箱图。
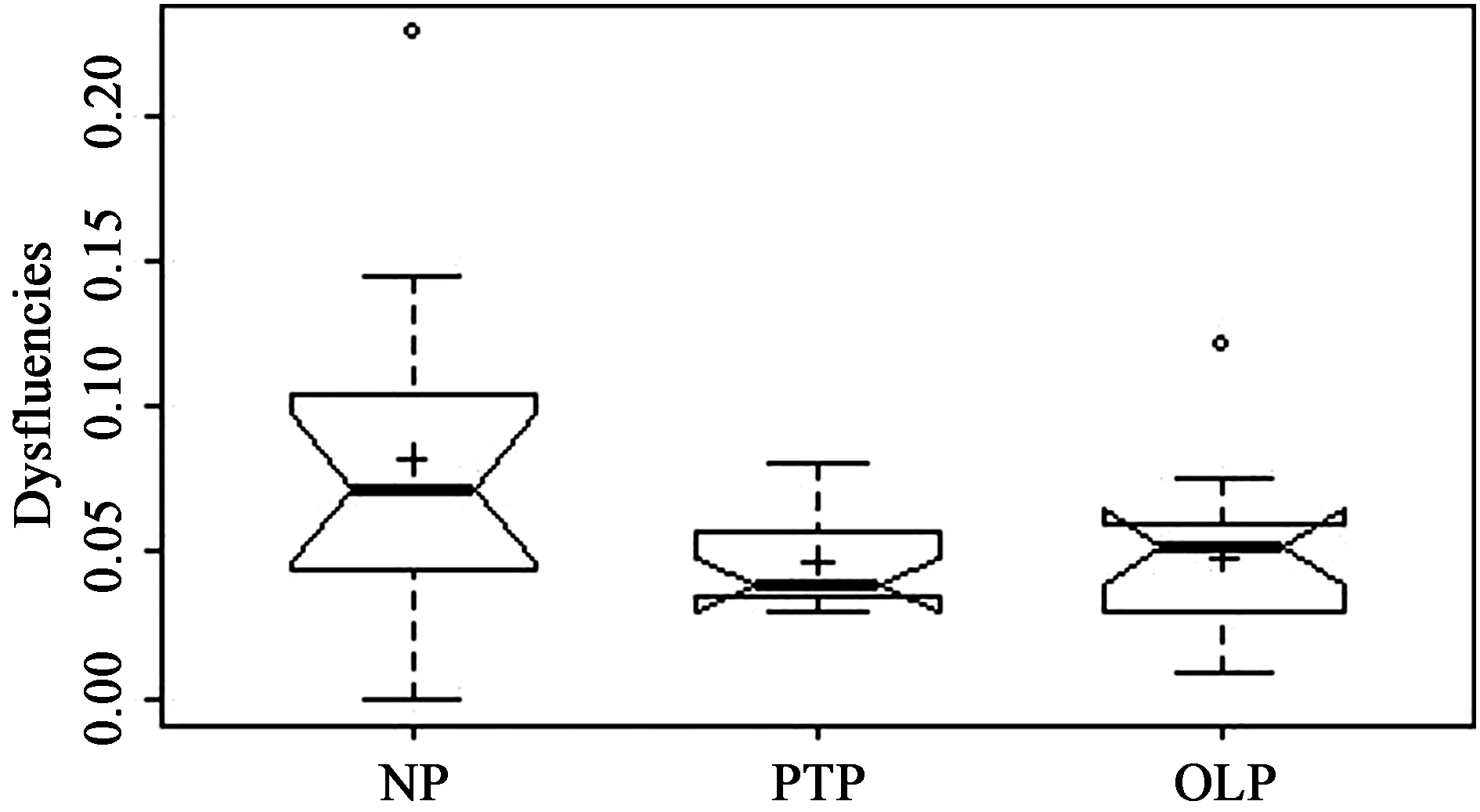
图3 三个准备条件下非流利度箱图比较
为了使箱图能够更好地揭示数据的特点,图3在传统的箱图中增加了平均数(用加号“+”表示)和切口(notches)。切口显示中位数95%的置信区间。两幅箱图的切口不重合是两个中位数有差异的最有力证据。
总体上看,三个组数据分布的离散程度有较大差异。无条件组(NP)数据分布的离散程度最大,其次是在线准备组(OLP)数据分布,任务前准备组(PTP)数据分布最集中。Levene方差齐性检验发现,组间方差不齐(F(2,39) = 4.45,p= .018< .05)。
图3显示的第2个重要特征是异常值的存在。无准备条件组和在线准备组数据有一个异常值。无条件组平均数轻度正向偏离中位数,主体数据分布较为匀称,但是较大的异常值使整体数据分布略正偏。在线准备组平均数与中位数几乎相同,数据分布不够对称,异常值使整体数据分布略正偏。任务前准备组数据没有异常值,平均数轻度正向偏离中位数,分布很不对称,呈正偏趋势。
图3显示的第3个重要特征是切口的重合度。无条件组的切口与其他两个条件组的切口有少量重合;任务前准备组和在线准备组切口的重合度高。
1.3.2 核密度图诊断
我们再利用核密度图诊断同一批数据。图4比较三个准备条件组非流利度数据核密度图。
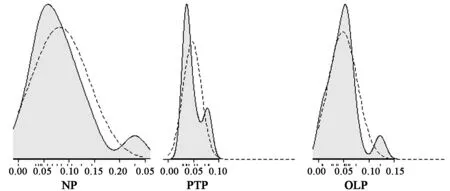
图4 三个准备条件下非流利度核密度图比较
图4中的实线为样本数据的分布曲线,虚线是为了对比而添加的正态分布曲线。为了便于数据性质诊断,图4还添加了轴须图,轴须代表非流利度测量值。同各自的正态分布曲线相比,三个准备条件组数据均呈单峰、正偏态分布。无准备条件组(NP)和在线准备组(OLP)数据分布肩部稍窄,分布曲线右尾各有一个凸块(即有一个异常值)。任务前准备组数据分布较陡峭,右侧有一个较高的凸块。这个凸块是由三个较大值引起的。虽然箱图没有将这三个值诊断为异常值,但是它们使肩部变宽。相对于其他两个准备条件组数据,任务前准备组数据违反正态分布的程度较为严重。另外,由于图4的横坐标采用同样的刻度值,因而很容易看出,无条件组数据分布最分散,其次是在线准备组数据分布,任务前准备组数据分布最集中。
综上所述,不论采用箱图还是核密度图,它们均表明本例数据违反常规方差分析的两个重要统计假设——正态分布和方差齐性,违反的程度似乎不严重。不过,统计假设违反程度严重性的判断尚没有公认的标准。
2 被试间设计稳健方差分析及应用
2.1被试间设计稳健方差分析
被试间设计稳健统计最常用的方法之一是稳健方差分析。本节介绍的稳健方差分析利用20%截尾平均数*将一组数据由小到大排序,然后从两端截除样本20%的数值,由此得到剩余数值的平均数即为20%截尾平均数。和Welch 方法(Welch’s method)的推广式。20%截尾平均数解决数据分布问题(如偏态分布和异常值),Welch方法处理组间方差不齐问题。因此,这种稳健方差分析方法又称截尾平均数比较WelchF检验。
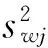
2.2被试间设计稳健方差分析应用
Ellis et al.(2004)采用的常规单因素方差分析方法以及配对检验方法(Scheffé检验)对三个准备条件开展推理统计。单因素方差分析发现三个准备条件在非流利度测量上有统计显著性差异(F(2,39) = 3.75,p= .032 < .05)。*Ellis & Yuan(2004)报告的F值为3.74。但是,Scheffé检验发现配对比较均没有显著性差异(无准备和任务前准备:p= .066 > .05,d= 0.93;无准备和在线准备:p= .080 > .05,d= 0.78;任务前准备和在线准备:p= .996 > .05,d= 0.06)*当综合方差分析发现某个因素有显著效应时,通常认为至少有一个配对比较有显著性差异。本例研究样本量较小,作者采用非常保守的Scheffé检验导致综合检验与配对检验结果矛盾。作者似应兼顾第一类错误率和统计效力。在正态分布和方差齐性条件下,d = 0.20、d = 0.50、d = 0.80依次表示小、中、大效应(Cohen,1988)。由于本例数据违反方差分析统计假设,效应量估计Cohen’s d不准确。。虽然本例中使用常规统计方法未必一定为误,但是根据前面的图示描述,我们至少可以认为这些传统的方法不是很恰当的方法。稳健组间比较方法是恰当的选择。
3 LOWESS平滑方法及应用
3.1 LOWESS平滑方法
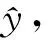
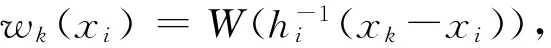
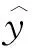
3.2 LOWESS平滑方法应用
在相关分析、协方差分析和回归分析中,LOWESS平滑方法用于诊断变量之间的线性或非线性关系。本节以French et al.(2008)收集的数据为例,利用LOWESS平滑方法诊断协方差分析中的线性与回归斜率齐性假设问题。
French et al.(2008)利用前后测实验设计调查音位记忆力、词汇知识和语法知识前测等多个变量对英语学习者语法知识发展的预测力。该研究收集的数据包括学生性别和接受性词汇知识前后测,不过研究者在回归分析中没有考虑性别因素。本节利用French et al.(2008)的数据回答另外一个问题,即在排除接受性词汇知识前测的影响后(简称词汇知识前测),性别是否对接受性词汇知识后测(简称词汇知识后测)有显著影响。
本例设计为单因素协方差分析设计。在推理统计之前,需要探索数据分布的模式,特别要诊断词汇知识前后测之间是否为线性关系,回归斜率是否齐性。
利用箱图与核密度图开展正态分布和方差齐性诊断发现,本例数据接近正态分布,只是女性词汇知识前测数据有三个相同异常值,男性词汇知识前测数据分布略呈双峰状,男性词汇知识后测数据有一个异常值。男、女生词汇知识后测数据方差不齐(F(1,102 )= 4.64,p= .034 < .05)。词汇知识前后测关系如图5所示。
图5左分图显示词汇知识前后测整体数据之间的关系,右分图显示男、女生词汇知识前后测数据之间的关系,图中的曲线为LOWESS平滑线,数据点用不同的符号显示。左分图表明,词汇知识前后测没有异常点,没有明显的方差不齐现象。LOWESS平滑线接近直线,且坡度较陡,说明它们之间有很强的线性关系。但是,右分图显示词汇知识前后测之间的关系随性别的变化而变化。在女生数据中,词汇知识前后测LOWESS平滑线近似为直线,且坡度较陡,反映较强的线性关系。但是,在男生数据中,当词汇知识前测值较小(约小于33)时,词汇知识前后测LOWESS平滑线较为水平;当词汇知识前测值较大(约大于33)时,词汇知识前后测LOWESS平滑线变得陡峭。这表明,词汇知识前后测在男生数据中存在非线性关系。另外,右分图两条平滑线交叉,说明词汇知识前后测回归线在性别的两个水平上非齐性。进一步的回归斜率齐性检验发现,本例数据违反回归斜率齐性假设(F(1,100 = 7.33,p= .008 < .01))。
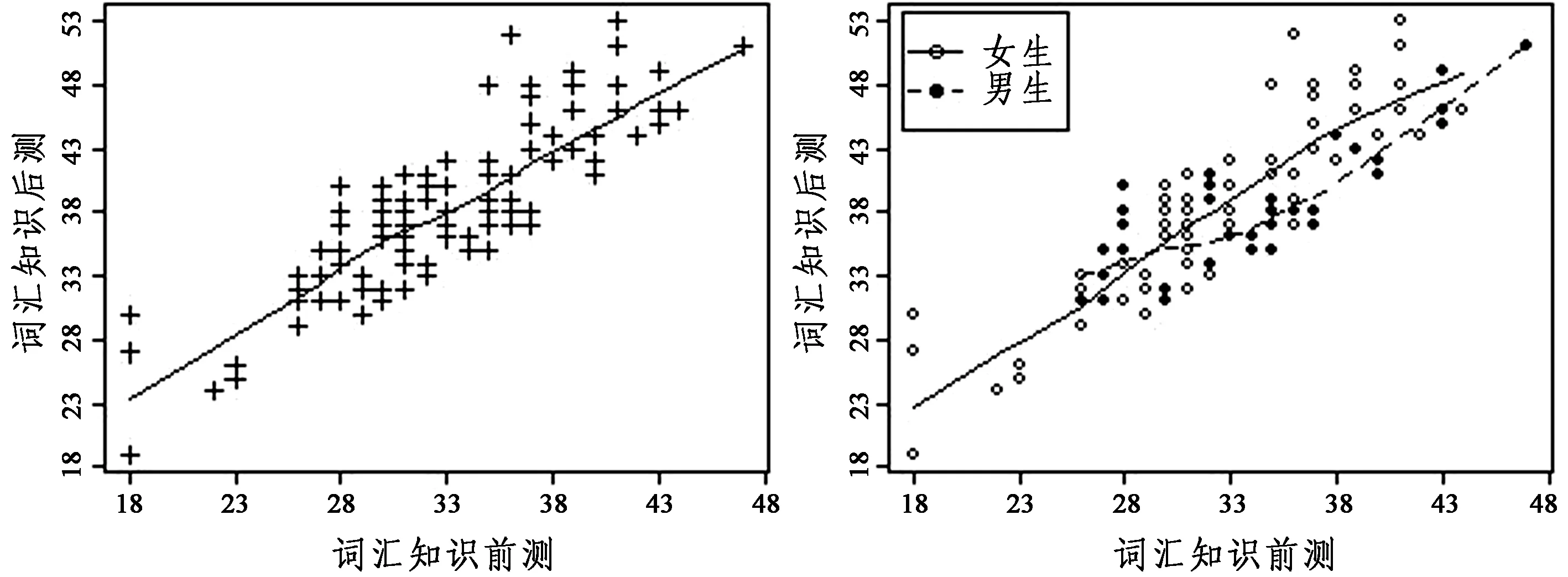
图5词汇知识前后测之间的关系
概而言之,本例数据分布有异常值和双峰现象存在,LOWESS平滑方法诊断发现词汇知识前后测违反回归斜率齐性假设,且在男生数据中词汇知识前后测之间存在非线性关系,因而常规的协方差分析方法不再适合用于推理统计。
4 非线性条件下稳健协方差分析及应用
4.1非线性条件下稳健协方差分析
在两个独立组的协方差分析中,如果协变量和因变量之间的关系为非线性关系,回归斜率非齐性(即回归线不平行),则常规协方差分析方法不再合适,宜选择稳健协方差分析方法——选点分析。
两组有条件的位置测量(如20%截尾平均数)记作mj(x),其中j= 1,2。选点分析的零假设是:H0:m1(x)=m2(x),其中x∈{x1,…,xK},K为协变量X选点数。计算条件估计量mj(x)必须要确定在某个协变量值x邻近的所有X值xij。一种确定方法是移动区间平滑方法(running interval smoother)(Wilcox,2017:628)。邻近值的判断标准为:|xi-x|f×MADN,其中f是平滑参数(常用值为1或0.8),MADN表示正态化的中位数绝对离差(参见鲍贵,2017)。根据邻近值的判断标准得到邻近xi的所有xj值的集合,记作N(xi)。令i为满足条件式j∈N(xi)的所有yj值的参数估计。计算所有x=xi(i=1,…,n) 时的i值,将(x1,1),…,(xn,n)连成线便得到回归线的图示表征。这一过程称作移动区间平滑方法。
通常在五个点上选择可比较的回归线。依据Wilcox(2017:703-704),设5个选择点为z1、z2、z3、z4和z5。协变量xij值按升序排列,即x1j≤ … ≤xnjj。因变量y值的次序与xij值的顺序对应。令Mj(x)是第j组邻近x的数据点数。在第一组中寻找满足条件式M1(xi1)≥12的协变量X最小值xi1。如果M2(xi1)≥12,则z1=xi1。如果M2(xi1)<12,寻找下一个X最小值xi1,照此重复直到满足条件式M1(xi1)≥12和M2(xi1)≥12。令i1是一个i值,是满足条件式M1(xi11)≥12和M2(xi11)≥12的最小整数,则z1=xi11。按照同样的方法得到最大选点z5=xi51。令i2=(i1+i3)/2,i3=(i1+i5)/2,i4=(i3+i5)/2。取i2、i3和i4的整数部分,则z2=xi21,z3=xi31,z4=xi41。
在稳健型选点分析中,令mj(x)为i满足条件式Nj(x) = {i:|xij-x|fj×MADNj}的第j组所有yij值的20%截尾平均数。Mj(x)是用于估计mj(x)的所有yij值的点数。根据Wilcox(2017: 703),当某个选点x上有效样本量足够大时(比如大于12),则在点x上两条回归线具有可比性,Yuen方法能够给出条件平均数差异m1(x)-m2(x)精确的置信区间。在多个x点上比较条件平均数差异时,可以利用Hochberg方法等控制族第一类错误率。
4.2非线性条件下稳健协方差分析应用
由于非线性条件下选点分析允许非正态分布、回归线非线性和非齐性,因而对第3节关于词汇知识前后测数据的推理统计适合采用稳健选点分析方法。表1报告选点分析的结果,调整p值控制族错误率的方法为Hochberg方法。
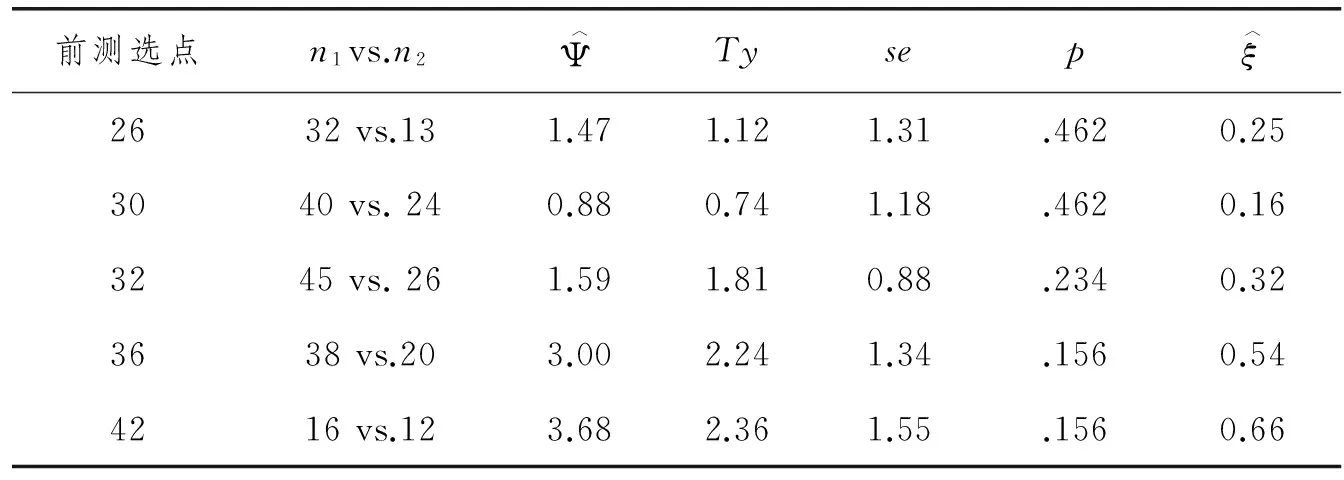
表1 性别对词汇知识后测影响的选点分析
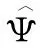
表1显示,在词汇知识前测的五个选点上,男、女生在词汇知识后测上均没有统计显著性差异(ps > .05)。换言之,在控制词汇知识前测时,性别对词汇知识后测没有统计显著性影响。如果针对本例采用常规协方差分析,则得到性别对后测有显著性效应的结论(F(1,101)= 6.92,p= .010 < .05),效应量达到中等水平(Cohen’sd= 0.54)。
从表1效应量来看,在前两个选点上,性别效应量低,而在最后三个选点上,效应量或接近中等水平,或达到中等甚至更大的水平。这似乎表明,在词汇知识前测的不同水平上,性别对词汇知识后测的影响是不一致的。如果研究者认为达到中等以上水平的效应量有实际意义,则在词汇知识前测较高水平(选点为36和42)上,女生比男生在词汇知识后测上表现更好。本例词汇知识前测较高水平上的有效样本量偏小,在大样本情况下,女生在词汇知识后测方面是否显著好于男生尚需进一步的研究论证。
5 结语
本文简要介绍了箱图、核密度图和LOWESS平滑线、单因素稳健方差分析与协方差分析(选点分析)的基本原理和程序。案例分析表明,这些图形大大增加了我们对数据分布模式的感知,为推理统计分析方法的选择提供了重要的依据。当数据违反正态分布和方差齐性时,常规方差分析与稳健方差分析得出不同的结果。当双变量数据违反线性假设和回归斜率齐性假设时,传统的协方差分析得出误导性的结果。这些结果凸显了诊断数据分布和采用稳健统计分析方法的重要性。
Cleveland, W. S. 1979. Robust Locally Weighted Regression and Smoothing Scatterplots [J].AmericanStatisticalAssociation, 74(368): 829-836.
Cleveland, W. S. 1985.TheElementsofGraphingData[M]. Monterey, CA: Wadsworth Advanced Book Program.
Cohen, J.1988.StatisticalPowerAnalysisfortheBehavioralSciences(2nd ed.) [M]. Hillsdale, NJ: Lawrence Erlbaum Associates.
Ellis, R. & F. Yuan. 2004. The Effects of Planning on Fluency, Complexity, and Accuracy in Second Language Narrative Writing [J].StudiesinSecondLanguageAcquisition(26): 59-84.
Emerson, J. D. & J. Strenio. 1983. Boxplots and Batch Comparison [G]∥ D. C. Hoaglin, F. Mosteller & J. W. Tukey.UnderstandingRobustandExploratoryDataAnalysis. New York, NY: Wiley,58-96.
French, L. M. & I. O’Brien. 2008. Phonological Memory and Children’s Second Language Grammar Learning [J].AppliedPsycholinguistics, 29(1): 1-25.
Gries, S. Th. 2013.StatisticsforLinguisticswithR:APracticalIntroduction(2nd ed.) [M]. Berlin/Boston: De Gruyter Mouton.
Hintze, J. L. & R. D. Nelson. 1998. Violin Plots: A Box Plot-Density Trace Synergism [J].TheAmericanStatistician, 52(2): 181-184.
Hyndman, R. J. & Y. Fan. 1996. Sample Quantiles in Statistical Packages [J].TheAmericanStatistician, 50(4): 361-365.
Johnson, K. 2008.QuantitativeMethodsinLinguistics[M] Malden, MA: Blackwell Publishing.
Kabacoff, R. I. 2015.RinAction:DataAnalysisandGraphicswithR(2nd ed.) [M]. Shelter Island, NY: Manning Publications Co.
Keen, K. J. 2010.GraphicsforStatisticsandDataAnalysiswithR[M]. Boca Raton, FL: Chapman & Hall/CRC.
Larson-Hall, J. 2012. Our Statistical Intuitions May Be Misleading Us: Why We Need Robust Statistics [J].LanguageTeaching, 45(4): 460-474.
Larson-Hall, J. 2016.AGuidetoDoingStatisticsinSecondLanguageResearchUsingSPSSandR(2nd ed.) [M]. New York, NY: Routledge.
Larson-Hall, J. & R. Herrington. 2010. Improving Data Analysis in Second Language Acquisition by Utilizing Modern Developments in Applied Statistics [J].AppliedLinguistics, 31(3): 368-390.
Larson-Hall, J. & L. Plonsky. 2015. Reporting and Interpreting Quantitative Research Findings: What Gets Reported and Recommendations for the Field[J].LanguageLearning, 65 (1): 127-159.
McGill, R., J. W. Tukey & W. A. Larsen. 1978. Variations of Box Plots [J].TheAmericanStatistician, 32(1): 12-16.
Plonsky, L. 2014. Study Quality in Quantitative L2 Research (1990—2010): A Methodological Synthesis and Call for Reform [J].TheModernLanguageJournal, 98(1): 450-470.
Plonsky, L., J. Egbert & G. T. LaFlair. 2015. Bootstrapping in Applied Linguistics: Assessing Its Potential Using Shared Data [J].AppliedLinguistics, 36(5): 591-610.
Silverman, B. W. 1986.DensityEstimationforStatisticsandDataAnalysis[M]. London: Chapman & Hall.
Tukey , J. W. 1977.ExploratoryDataAnalysis[M]. Reading, MA: Addison-Wesley.
Ugarte, M.D., A. F. Militino & A. T. Arnholt. 2015.ProbabilityandStatisticswithR(2nd ed.) [M]. Boca Raton, FL: CRC Press.
Wilcox, R.R. 1998. How Many Discoveries Have Been Lost by Ignoring Modern Statistical Methods? [J].AmericanPsychologist, 53(3): 300-314.
Wilcox, R. R. 2012.IntroductiontoRobustEstimationandHypothesisTesting(3rd ed.) [M]. San Diego, CA: Elsevier.
Wilcox, R. R. 2017.IntroductiontoRobustEstimationandHypothesisTesting(4th ed.) [M]. San Diego, CA: Elsevier.
鲍贵. 2012. 我国外语教学研究中的统计分析方法使用调查 [J]. 外语界(1):44-51,60.
鲍贵. 2014. 研究设计中样本量的确定 [J]. 外国语文(5):115-121.
鲍贵. 2016. 输出任务类型和词语意象性对英语学习者词汇习得的影响 [J]. 外语与外语教学(6):56-65,74.
鲍贵. 2017. 语言学定量研究中的稳健统计方法 [J]. 外语研究(2):22-29.

