振动的等效力传递路径分析方法研究

潘运平，颜为光，王 飞

（武汉理工大学 机电工程学院，湖北 武汉 430070）

1 引言

经典传递路径分析（Transfer Path Analysis，TPA）方法已被证明是一种分析振动的可靠方法，并在机床、汽车、船舶、飞机等领域的振动问题中被广泛应用[1-2]。对于振动问题，经典TPA法一般首先拆解系统获得振源激励-响应传递函数，然后获得工况激励，最后计算不同振源的贡献。由于实际中振源及安装结构的复杂性，工况激励的准确获取非常困难。同时，拆解系统的工作非常繁琐耗时。

假设一组作用于静止状态下系统中激励源与结构连接处的等效力，可以在结构中重构出与系统工况运行时相同的响应，则可以利用这组等效力表征激励源[3-5]。针对经典TPA法研究振动问题时的激励力测量和系统拆解问题，在经典TPA法中对每个振源均引入一组作用于该振源与结构连接处的等效力代替激励力以改进经典TPA法。由于等效力的计算涉及导纳矩阵求逆问题，使用正则化方法来解决求逆时易出现的病态问题。搭建电机工作平台并进行振动实验验证，结果证明了正则化方法解决导纳矩阵病态问题的可行性及改进方法即振动的等效力传递路径分析方法预测振动响应和计算振源贡献的准确性。

2 经典TPA法理论

2.1 经典TPA法

传递路径研究系统的传递特性[6]，对于振动问题，经典TPA法的理论如下：

式中：Fi—振源激励力；Hi—传递函数；a—目标点响应；FiHi—第i个振源对目标点响应的贡献[7]。需要注意：式（1）计算过程每次都是在单个频率点进行的。

经典TPA法的一般步骤为：首先拆解系统并施加人工激励以直接测量或利用互易法间接测量振源激励力到目标点响应的传递函数；然后通过直接法或间接法获得工况激励力。之后即可按照式（1）预测目标点响应和计算源的贡献[8]。其中，获得工况激励的常用方法有直接测量法、悬置刚度法及逆矩阵法[9]。

2.2 经典TPA法的局限性

经典TPA方法虽然结果可靠，但是也存在一些局限性：（1）实际的振源及安装结构比较复杂，因此准确获取工况激励力较为困难。（2）获取传递函数时需要拆解系统，繁琐耗时。同时拆解实际上改变了系统工况运行时的边界条件，而实际系统多少存在一定的非线性，因此会引起一定的误差。

3 振动的等效力传递路径分析方法

3.1 利用等效力表征振源改进经典TPA法

除了用激励力表征激励源外，还可以寻找一组作用于静止状态下系统中激励源与结构连接处的等效力来表征，要求是等效力可以使系统产生与系统工况运行时相同的响应[4-5]。

针对经典TPA法研究振动问题时激励力实时测量困难以及系统拆解工作繁琐问题，在经典TPA法中引入等效力代替传统激励力，即对每个振源都用一组作用于振源与结构连接处的等效力表征，然后按照与经典TPA法类似的步骤预测振动响应和计算振源贡献，从而形成了改进方法，即振动的等效力传递路径分析方法。这不仅解决激励力实时测量问题，还避免了拆解系统，因此更加方便可行。具体操作步骤如下：（1）对每个振源，选取分布于该振源与结构连接处若干点作为等效力作用点，即用一组作用于这些等效力点的等效力来表征该振源。为了能够预测结构上关心响应点即目标点的振动响应和计算不同振源对目标点响应的贡献，在结构上选择若干响应点即参考点用于计算等效力，要求参考点尽量分散，避免集中或对称，且参考点数量要大于等效力数量。（2）通过人工激励获得所有等效力点到参考点和目标点的激励-响应传递函数，构造加速度导纳矩阵。设某目标点振动响应为，则目标点响应与等效力之间的关系为：

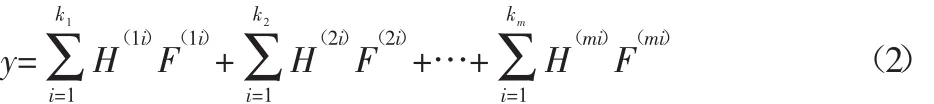
式中：m—系统中振源的数量；kj—对于第j个振源用kj个等效力来表征，表征不同振源的等效力数量不一定相同；F（ji）—表征第 j个振源的第 i个等效力；H（ji）—等效力 F（ji）到目标点响应的传递函数。将式（2）写成矩阵形式，即：

式中：［H（11）H（12）… H（1k1）… H（mkm）］—目标点导纳矩阵。

设参考点振动响应为x，则参考点振动响应与等效力之间的关系为：

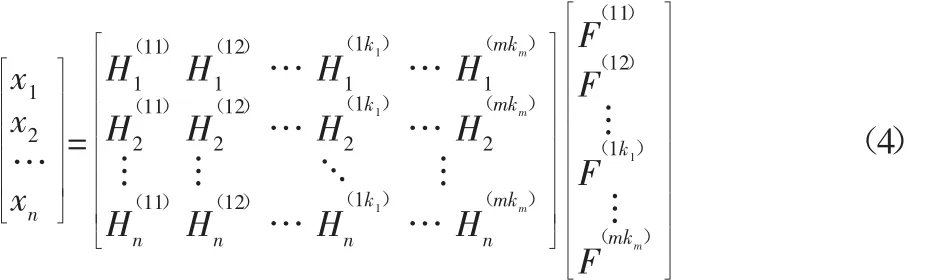
式中：n—参考点数量，要求参考点数量大于或等于等效力数量，即n≥k1+k2+…+km；xp—第p个参考点的响应；kj—表征第j个振源的等效力的数量；F（ji）—表征第j个振源的第i个等效力—等效力F（ji）到第p个参考点响应的传递函数。

式中：H—参考点导纳矩阵。

（2）在工况运行条件下，测量结构上参考点响应Xope，利用式（5）即可计算该工况下的等效力为：

式中：Fope—该工况下的等效力，且满足：然后即可按式（2）预测目标点的响应即：

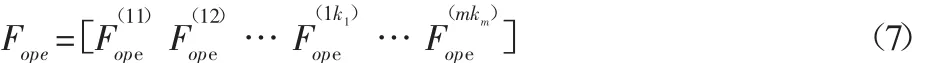
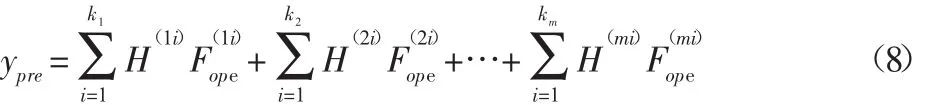
式中：ypre—目标点响应的预测值；

3.2 正则化方法解决病态问题

在利用参考点响应求工况激励时，为了保证参考点导纳矩阵的逆矩阵存在，通常要求参考点数量大于等效力数量，则等效力的具体计算步骤如下[10]：对式（5）中的参考点导纳矩阵H进行奇异值分解得到：

式中：k—等效力总数量；k=k1+k2+…+km，U=（u1，…，km）和V=（v1，…，vk）—单位列正交向量矩阵；VT—V的共轭转置矩阵；Σ—对角矩阵，位于对角上的σi为奇异值并且σ1≥…≥σk≥0。

设r为正奇异值的个数，若直接用最小二乘法求解等效力，则结果为：

由于结构模态以及测量噪声的影响，H中通常会出现较小的特征值。由式（10）可以看出，由于这些较小的特征值的存在，参考点响应Xope中较小的误差也会在求得等效力Fope中造成较大的误差，即导纳矩阵易出现病态问题。Tikhonov正则化是目前解算病态问题应用较为普遍的一种方法，因此选用Tikhonov正则化来解决导纳矩阵的病态问题。Tikhonov正则化方法求解等效力的准则为：

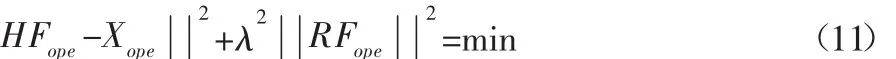
式中：λ—正则化参数；R—正则化矩阵；· —欧式（2）-范数。

当 R=Ik时，根据式（9）及式（11）可得 Tikhonov正则化方法求得等效力为：

可以看出，Tikhonov正则化方法可以削弱较小奇异值的影响，从而改善原矩阵的不适定性以得到稳定的解。确定正则化参数λ的大小通常用L曲线法或GCV（广义交叉验证）法，选用L曲线法。L曲线法的合理性在于它强调残余范数||HFope-Xope||与正则化解范数||Fope||之间的平衡，而这种平衡是通过参数λ来实现的。

4 振动的等效力传递路径分析方法验证

4.1 验证试验

为验证正则化方法解决导纳矩阵病态问题的可行性以及振动的等效力传递路径方法的准确性，设计了小型电机实验平台进行实验验证

4.1.1 实验系统、测点布置以及等效力点选择

实验系统主要由实验平台和测试采集系统构成。实验平台主要是由2个小型直流电机和1块（1000×1000×3）mm的钢板组成。钢板四个角落通过软垫由四个刚性支座支撑，两电机刚性安装在钢板背面，钢板正面布置加速度测点，钢板正面和背面电机布置，如图1所示。测试采集系统主要包括加速度传感器、力锤、B＆K采集设备以PULSELabShop测试软件，实验主要仪器，如图2所示。

图1 实验平台Fig.1 Experiment Platform

图2 试验主要仪器Fig.2 Main Test Instruments

设钢板背面两电机分别为1号和2号电机，其与钢板连接位置对应钢板正面区域分别为#1和#2区域，则在#1和#2区域各选择均匀分布的5个点作为等效力作用点，即对每个电机各用作用于该电机与钢板连接处的5个等效力来表征其激励，则本实验中2个电机一共用了共10个等效力来表征，两组等效力作用点位置分别如图3中#1位置和#2位置所示。在钢板正面随机选择15个点作为结构响应点并安装加速度传感器，命名为1号点到15号点，其位置分布，如图3所示。

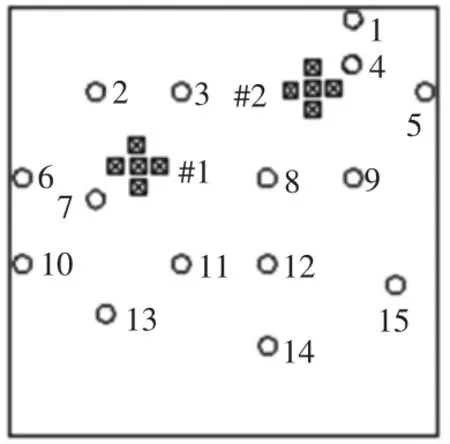
图3 电机和等效力位置及测点布置示意图Fig.3 Motors and Equivalent Forces’Positions and Measuring Points’Layout Diagram

4.1.2 实验过程

设14号点和15号点为目标点，选取1号～13号点为参考点，然后即可进行基于振动的等效力传递路径分析方法的电机平台振动实验，具体步骤为：

（1）进行力锤敲击获取传递函数，在每个等效力点进行3次敲击，经平均后计算出（13×10）维的参考点导纳矩阵和两个（1×10）维的目标点导纳矩阵；

（2）让两个电机各以一定转速同时运行，测量混合运行工况下15个测点的响应；

（3）按照分布运转法让两电机按混合工况时转速各单独运行3次，测量并经平均后计算单开工况下两目标点的响应，将其作为两电机对两目标点响应贡献的实测值。

首先根据混合工况时参考点响应按公式（6）计算工况等效力，然后按公式（8）计算两电机对目标点响应的贡献并预测两目标点响应。将响应预测值与混合工况时实测值对比，即可验证该方法预测响应是否准确，将贡献计算值与分布运转法所得实测值对比，即可验证振源贡献计算是否准确。

4.2 实验结果分析

为检验正则化方法解决导纳矩阵病态问题的效果，在利用振动的等效力传递路径分析方法计算分析过程中，分别采用直接最小二乘法和Tikhonov正则化方法计算求解等效力，将最终结果进行对比，其中Tikhonov正则化方法的正则化参数用L曲线法确定。两目标点响应的预测值与实测值及两电机对两目标点贡献的计算值与实测值的1/3倍频程幅值谱对比，如图4～图9所示。

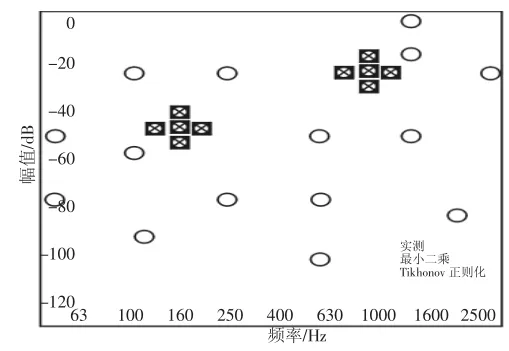
图4 14号点响应实测值与预测值对比Fig.4 Comparison of the Measured and Predicted Value of the 14th Point’s Response

图5 1号电机对14号点响应贡献实测值与计算值对比Fig.5 Comparison of the Measured and Evaluated Value of No.1 Motor’s Contribution to the 14th Point’s Response

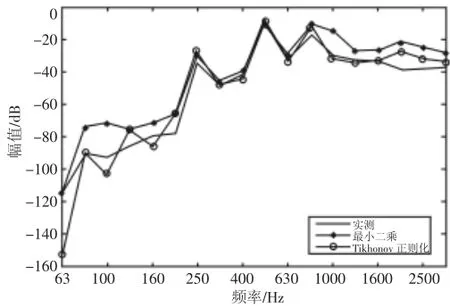
图6 2号电机对14号点响应贡献实测值与计算值对比Fig.6 Comparison of the Measured and Evaluated Value of No.2 motor’s Contribution to the 14th Point’s Response

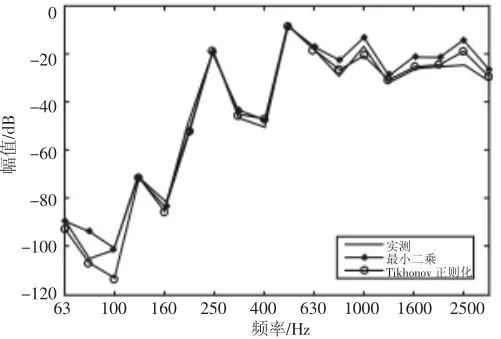
图7 15号点响应实测值与预测值对比Fig.7 Comparison of the Measured and Predicted Value of the 15th Point’s Response

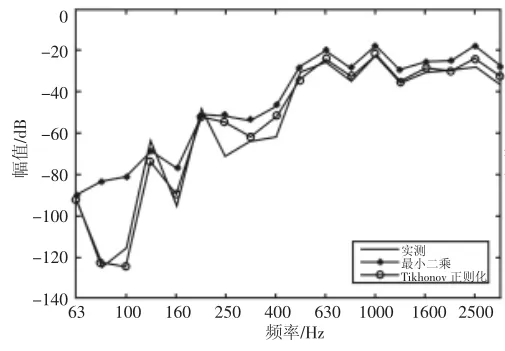
图8 1号电机对15号点响应贡献实测值与计算值对比Fig.8 Comparison of the Measured and Evaluated Value of No.1 Motor’s Contribution to the 15th Point’s Response

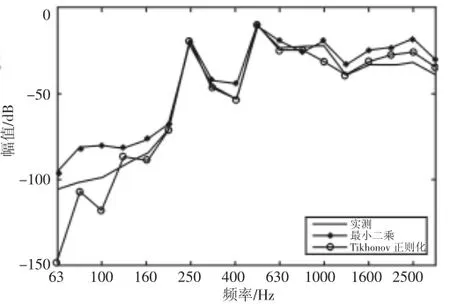
图9 2号电机对15号点响应贡献实测值与计算值对比Fig.9 Comparison of the Measured and Evaluated Value of No.2 motor’s Contribution to the 15th Point’s Response

为加深对验证效果的理解，进一步求所得结果在整个频段的总加速度级计算误差，其计算公式为：

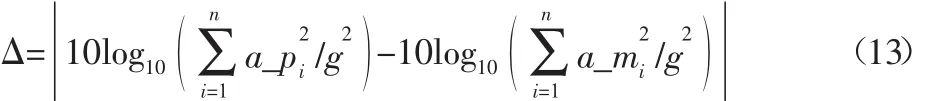
式中：Δ—总加速度级计算误差，n为1/3倍频程数；

a_pi—在第i个频程加速度响应预测值或贡献计算值；

a_mi—在第i个频程加速度响应或贡献的实测值；

g—重力加速度常数，直接用最小二乘法和用正则化方法求等效力对应最终结果的总加速度级计算误差，如表1所示。

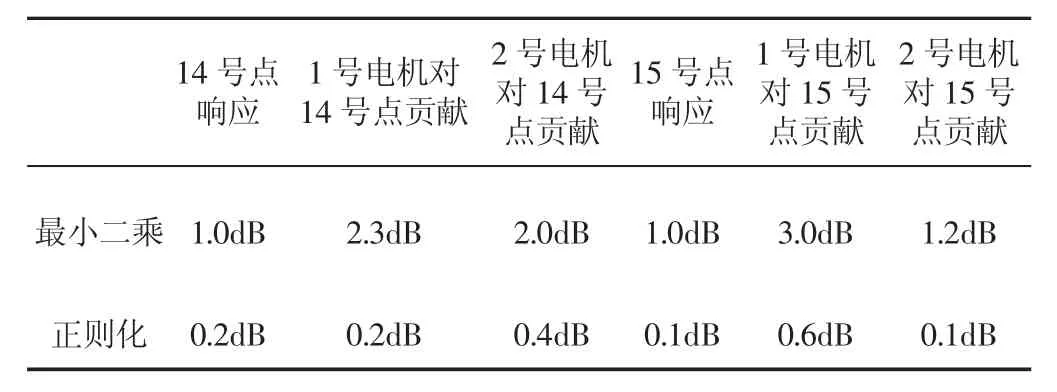
表1 两目标点响应及两电机贡献的总加速度级计算误差Tab.1 The Calculation Error of the Total Acceleration Level of the Two Target Points’Response and the Two Motors’Contributions

从曲线图来看，运用振动的等效力传递路径分析方法预测振动响应时，若使用正则化方法求等效力，则两目标点均是除个别频点外，在绝大多数频段，加速度响应的预测值与实测值的频谱吻合得非常好；而直接使用最小二乘法求等效力与正则化方法相比，其在高频段预测结果出现了较大的误差。在计算对目标点响应贡献时，若使用正则化方法求等效力，则除个别频点外，在绝大多数频段，两电机对两目标点贡献计算值均与分部运转法获得的实测值吻合得较好，但是若直接使用最小二乘方法求等效力，则与正则化方法相比，计算误差明显要大得多。这是由于结构模态以及测量噪声的影响，不同等效力作用点获得的传递函数之间相关性较大，导纳矩阵易出现病态，所以直接最小二乘法不是良好的计算方法，而正则化方法通过引入正则化系数，可以在有效地缓解导纳矩阵求逆过程中的不适定问题，提高等效力求解的稳定性，所以计算结果较为吻合。

从表1来看，使用正则化方法求等效力，振动的等效力传递路径分析方法无论是预测目标点响应还是计算电机对目标点的贡献，其结果在整个频段内的总加速度级误差均非常小，而若直接使用最小二乘法求等效力，则其结果的总加速度级误差要大得多，这再次验证了上述结论。实验结果说明：正则化方法可以有效解决求等效力过程中的导纳矩阵病态问题，改进方法即振动的等效力传递路径分析方法可以较准确地预测振动响应和计算振源的贡献。

5 结论

在利用经典传递路径分析（Transfer Path Analysis，TPA）方法预测系统振动响应和计算振源的贡献时，不仅激励力的实时测量比较困难，而且系统拆解繁琐耗时。针对该问题，通过在经典TPA法中引入等效力代替传统的激励力，即对系统中每个振源均用作用于该振源与结构连接处的一组等效力来表征该振源以改进经典TPA法，并利用正则化方法解决导纳矩阵求逆时易出现的病态问题，改进的方法即振动的等效力传递路径分析方法不仅解决了激励力实时测量问题，还避免了系统拆解工作，因此更为简单可行。搭建电机实验平台对该方法进行振动实验验证，结果表明：正则化方法可以解决导纳矩阵病态问题，振动的等效力传递路径分析方法可以较为准确地预测系统振动响应和计算振源贡献。

［1］方德广，祖庆华，史文库.轻型客方向盘怠速抖动问题的传递路径分析［J］.机械设计与制造，2016（3）：61-64.（Fang De-guang，Zu Qing-hua，Shi Wen-ku.Transfer Path Analysis of the Light Bus Steering Wheel Wobbling Problem in Idle［J］.Machinery Design and Manufacture，2016（3）：61-64.）

［2］乔宇峰，黄其柏，李天匀.工况传递路径分析（OPA）方法在应用中的缺陷［J］.噪声与振动控制，2010，30（5）：132-136.（Qiao Yu-feng，Huang Qi-bai，Li Tian-yun.Application Limitations of Operational Transfer Path Analysis［J］.Noise and Vibration Control，2010，30（5）：132-136.）

［3］De Klerk D，Rixen D J.Component Transfer Path Analysis Method with Compensation for Test Bench Dynamics［J］.Mechanical Systems and Signal Processing，2010，24（6）：1693-1710.

［4］Van der Seijs M V，de Klerk D，Rixen D J.General framework for transfer path analysis：History，theory and classification of techniques［J］.Mechanical Systems and Signal Processing，2016（68）：217-244.

［5］Janssens M H A，Verheij J W，Thompson D J.The Use of an Equivalent Forces Method for the Experimental Quantification of Structural Sound Transmission in Ships［J］.Journal of Sound and Vibration，1999，226（2）：305-328.

［6］曹跃云，张磊，杨自春.船舶振动噪声源传递路径分析及试验验证［J］.振动与冲击，2013，32（22）：158-162.（Cao Yue-yun，Zhang Lei，Yang Zi-chun.A New OPA Model for Ship Noise Sources and Test Validation［J］.Journal of Vibration and Shock，2013，32（22）：158-162.）

［7］刘东明，项党，罗清.传递路径分析技术在车内噪声与振动研究与分析中的应用［J］.噪声与振动控制，2007，27（4）：73-77.（Liu Dong-ming，Xiang Dang，Luo Qing.Applying Transfer Path Analysis to Automotive Interior Noise and Vibration Refinement and Development［J］.Noise and Vibration Control，2007，27（4）：73-77.）

［8］Plunt J.Finding and Fixing Vehicle NVH Problems With Transfer Path Analysis［J］.Sound and Vibration，2005，39（11）：12-17.

［9］卢英英，成玮，陆建涛.运行工况传递路径分析方法研究进展［J］.河北科技大学学报，2015，36（4）：359-367.（Lu Ying-ying，Cheng Wei，Lu Jian-tao.Research Progress of Operational Transfer Path Analysis Method［J］.Journal of Hebei University of Science and Technology，2015，36（4）：359-367.）

［10］范千，方绪华，范娟.病态问题解算的直接正则化方法比较［J］.贵州大学学报，2011，28（4）：29-32.（Fan Qian，Fang Xu-hua，Fan Juan.Comparison of Direct Regularization Methods of Ill-conditioned Problems［J］.Journal of Guizhou University，2011，28（4）：29-32.