电子自旋辅助实现光子偏振态的量子纠缠浓缩∗

赵瑞通 梁瑞生 王发强

(华南师范大学信息光电子科技学院,广东省微纳光子功能材料与器件重点实验室,广州 510006)(2017年3月4日收到;2017年8月20日收到修改稿)

1 引 言

量子纠缠在量子信息处理过程中的角色至关重要,尤其是在远距离量子通信过程中,量子纠缠经常被用做量子通道连接远距离的两个节点.然而,在量子纠缠通道的分配设置过程中和通道建立后,纠缠不可避免地会受到通道和周围环境噪声的影响而降低,这就降低了远距离量子通信的保真度和安全性.为了获得高品质的量子纠缠通道来实现远距离量子通信,需要用到纠缠浓缩方案[1−4].纠缠浓缩就是从纠缠程度较低的部分纠缠态中提取出纠缠程度较高的纠缠态甚至是最大纠缠态的方法.1996年,第一个纠缠浓缩方案被提出[1],这个方案是利用Schmidt投影方法实现的,而且要求两个参与者获得部分纠缠态的系数,也要用到联合非破坏测量技术.之后,人们提出了很多的纠缠态浓缩方法.文献[5,6]分别利用线性光学元件发展了Schmidt投影方法.Bose等[7]提出了基于纠缠交换的纠缠浓缩,这种方法需要用到联合Bell态测量.2008年,Sheng等提出了一个高效的纠缠浓缩方法,可以通过重复纠缠浓缩过程提高成功率[8],并在2012年将这个方案做了改进[9].随后,更多的纠缠浓缩方案相继出现,例如多粒子纠缠态浓缩,包括Greenberger-Horne-Zeilinger(GHZ)态[10,11],W态[12],团簇态[13]等,以及多维度的超纠缠浓缩[14−16].

自从1998年Loss和DiVinoenz[17]提出在半导体量子点中利用电子自旋作为量子比特以来,自旋半导体量子点系统就由于其容易操作和扩展,并且有较长的相干时间,成为最有希望实现量子计算机的方案之一.人们己经提出了非常多的基于自旋半导体量子点来实现量子通信和量子计算的方案[18−23],量子点结构还可以用作单光子源和纠缠光子源[24,25]等.Wang等[26]在2011年利用量子点和光学微腔的耦合系统构建了电子自旋态的宇称检测门,并在此基础上实现了自旋纠缠态的提纯和浓缩.随后,他们简化了这个方案,用一个量子点和一个单光子作为辅助来实现自旋纠缠态的浓缩[27].2013年,Sheng等[28]进一步简化了自旋纠缠态浓缩的方案,他们只用一个辅助单光子就可以得到最大纠缠态.同时,基于量子点-腔系统也可以实现光子态的纠缠浓缩.在量子点-腔系统中实现的超纠缠光子态浓缩在2014年被提出.Ren和Long[29]利用单边光学微腔中的量子点自旋实现了光子偏振和空间模自由度的宇称检测,并以此对光子偏振和空间模两个自由度上的纠缠态进行浓缩.这个方案的成功概率可以通过重复执行纠缠浓缩来进一步地提高,而且它可以推广到n光子超纠缠GHZ态的纠缠浓缩.

然而,以上的纠缠浓缩方案需要知道部分纠缠态的系数或者需要重复纠缠浓缩过程,这些都降低了纠缠浓缩的效率.本文探讨如何利用量子点-腔系统实现更加高效的光子偏振态纠缠浓缩.第2部分介绍量子点和双边光学微腔的相互作用;第3部分详细介绍光子偏振态的纠缠浓缩方案;第4部分讨论方案的保真度问题;第5部分是本文的总结.

2 量子点和双边腔的相互作用

将一个单电子的量子点嵌入光学微腔中,用抽运光对系统进行激发可以产生带负电的激子X−,这个激子是由两个电子的自旋和一个空穴的自旋共同组成的.根据泡利不相容原理,X−的跃迁由过剩电子的自旋态控制.这样会导致两种圆偏振光经过量子点系统时的透射和反射呈现不同的性质,透射和反射系数也会有不同的相位和振幅.

双边腔是指光学谐振腔的两端都可以作为光子的输出端,量子点被嵌在腔的中心.在双边腔系统中,光子的自旋是沿着腔的轴方向(z轴)的.根据光子自旋的不同,量子点-腔系统会产生两种典型的跃迁.根据选择定则,当过剩电子处于自旋向上的|↑〉态,只有|L〉态的左旋圆偏振光子被吸收,激子处于|↑↓⇑〉态.如果过剩电子处于自旋向下的|↓〉态,只有右旋圆偏振光子被吸收,激子处于|↓↑⇓〉态. 其中,|⇑〉和|⇓〉分别代表重穴自旋态|+3/2〉和|−3/2〉.如图1所示,双边光学腔有两个输出端口.

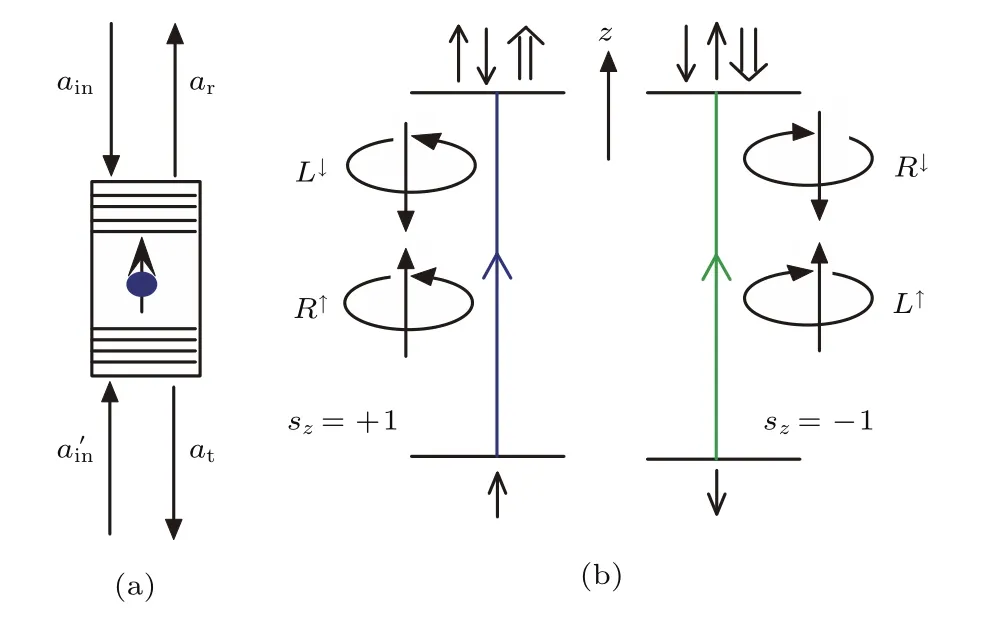
图1 (a)双边腔系统的圆截面,量子点被嵌在腔的中心;(b)量子点-腔系统的能级跃迁和光学选择定则(z表示双边腔的轴;L和R分别代表光子的左旋和右旋偏振态)Fig.1.(a)The circular cross section of bilateral cavity with a quantum dot embedded in the center;(b)the energy level transition and optical selection rule in quantum dot and cavity system.z is the axis of bilateral cavity.L and R denote the states of the left and right circularly polarized photons,respectively.

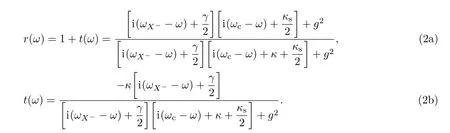
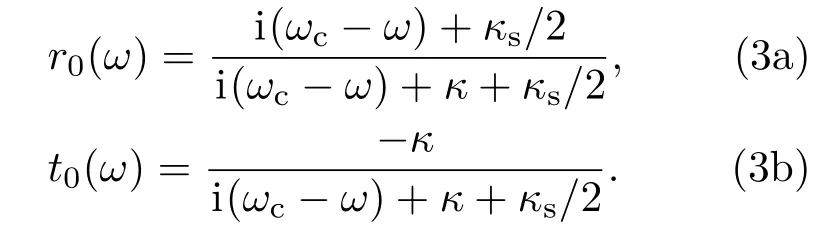
在强耦合和理想共振条件下,可以得到|t(ω)|→0,|t0(ω)|→1,|r(ω)|→1,|r0(ω)|→0.当量子点自旋态处于|↑〉时,sz=+1的光子即处于|R↑〉或|L↓〉的光子,会被反射,光子的偏振方向和传播方向都发生变化,变成|L↓〉或者|R↑〉.而sz=−1的光子即处于|R↓〉或|L↑〉的光子会被透射,并伴随着π相位的翻转.类似地,当量子点自旋态处于|↓〉时,sz=−1的光子会被反射,sz=+1的光子会被透射.以上跃迁规则可以用以下的变换来表示[31,32]:

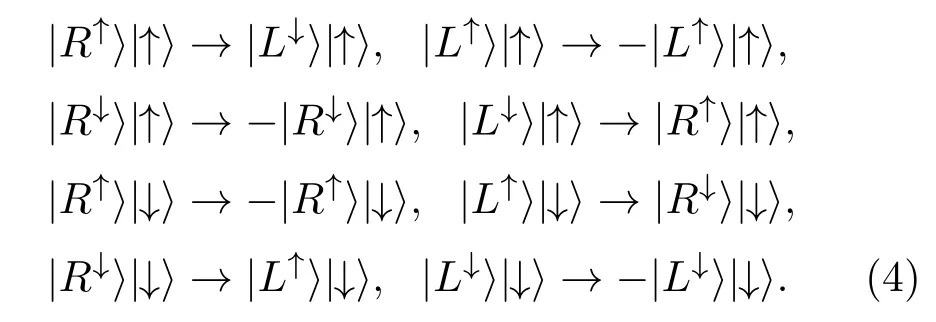
3 光子偏振态的纠缠浓缩

下面介绍偏振态纠缠浓缩的原理.假设两个距离很远的光子处于较低的纠缠态:

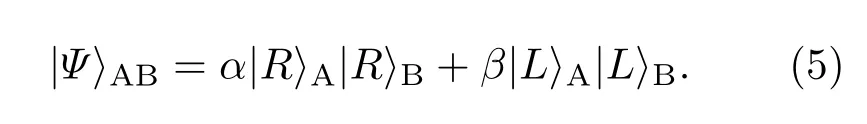
其中|α|2+|β|2=1. 下标A(B)分别表示参与者所持有的光子.辅助光子a处于单光子态|Ψ〉a=|R〉a.两个量子点中的电子处于自旋态下标s1(2)分别表示在光子A(B)位置的量子点.如图2所示,在光子A处,让光子a和A依次通过第一个量子点.光开关SW确保光子a首先通过,光子A后通过.光子a和A通过量子点的时间间隔应该小于量子点自旋的相干时间.在光子A通过量子点-腔系统之前,需要对自旋态执行一个Hadamard操作,即光子A通过量子点-腔系统后,再对自旋态执行一个Hadamard操作.最终,在通过第一个量子点-腔系统之后,光子和电子自旋的组合态变为然后,把辅助光子a传送给参与者B.在光子传送过程中,由于存在通道噪声,光子态会发生变化:|R〉→γ|R〉+δ|L〉(|γ|2+|δ|2=1). 利用偏振分束器C-PBS将光子通过两个可能的通道进行传送,并且在传送前和传送后都对通道2的光子执行σX操作.所以B可能在通道1或者2得到辅助光子a,这时,系统的态为

图2 光子偏振态纠缠浓缩的示意图(s1和s2分别代表第一个和第二个量子点的自旋;C-PBS代表偏振分束器,它透射|R〉光子并反射|L〉光子;SW是光开关,它被用来控制光子从不同的路径输出;HWP表示对光子执行σX操作的半波片;1和2分别代表辅助光子a可能通过的通道;D1,D2,D3和D4是单光子探测器)Fig.2.Schematic of polarization state entanglement concentration.s1and s2are quantum spin states.C-PBS denotes circular polarization beam splitter,transmitting|R〉photon and re fl ecting|L〉photon.SW denotes switch used to control the paths of photon.HWP represents the half wave plate to perform σXon photon.1 and 2 are the possible channels of photon a.D1,D2,D3,and D4are single-photon detectors.

与A类似,参与者B让光子a和B依次通过第二个量子点-腔系统.最后得到:

可以看到,根据两个量子点自旋态和辅助光子偏振态的测量结果,可以通过相应的单光子操作使光子A和B处于最大纠缠态现在,测量两个量子点的自旋态和辅助光子的偏振态,如果得到

4 讨 论

以上成功概率是在理想条件下计算的,没有考虑量子点-腔系统的耦合强度以及腔的泄漏对方案的影响.如果将耦合强度和腔泄漏率考虑进来,则需要计算系统量子态的保真度F=|〈Ψf|Ψ〉|2. 这里,|Ψf〉是包含外部环境影响时系统的最终态,而|Ψ〉是理想条件下的最终态. 本文以|R〉1|↑〉s1|↑〉s2的测量结果为例,来说明不同的因素对纠缠浓缩的保真度的影响.对于其他15种测量结果,都可以用同样的方法计算得到相对应纠缠态的保真度,得到的结果是类似的,只是在具体的数值上有些差异.当测量结果为|R〉1|↑〉s1|↑〉s2时,得到的纠缠态的保真度为其中,ξ=|t|2(|r|2+|t|2)+|r0|2(|t|−|t0|)2+2|r|2|t||t0|+(|r|2+2|t|2)|t0|2+|t0|4+2|r||r0|(|t0|2−|t|2),ζ=|r0|4+2|r||r0|(|t|2−|t0|2)+|r|2(|r|2+|t|2−2|t||t0|+|t0|2)+|r0|2(2|r|2+|t|2+2|t||t0|+|t0|2).可以看到,F随着|α−β|变化.|α+β|2+|α−β|2=2,所以图3是F随|α−β|的变化曲线.

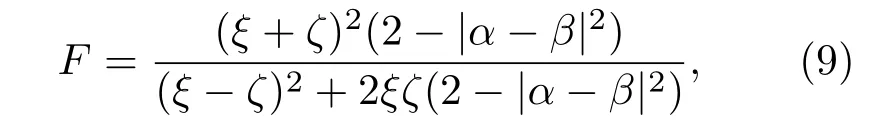
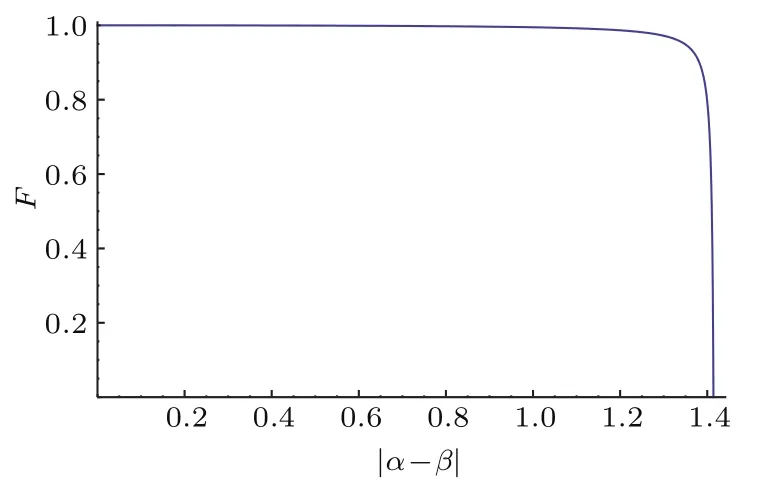
图3 保真度随初始纠缠态系数的变化曲线(这里选择腔泄漏率κs/κ=0,量子点-腔系统的耦合强度g/κ=1,并且γ/κ =0.2)Fig.3.The curve of fi delity vs initial coefficients of entangled state.The cavity leakage is chosen to be κs/κ =0,and coupling strength g/κ =1 with γ/κ =0.2.

从图3可以看出:当|α−β|≤ 1.3时,F变化很小,并保持接近于1的值.当|α−β|=1.3时,F=0.972;然而,当|α−β|＞1.3时,F将随着|α−β|的增加急剧减小.所以在|α−β|≤ 1.3时,本文的纠缠浓缩方案受部分纠缠态的初始信息影响很小,可以实现任意未知纠缠态的浓缩;然而,时,本文的方案保真度较小.

同时,保真度F也会受到耦合强度g/κ和腔边泄漏率κs/κ的影响,如图4所示.

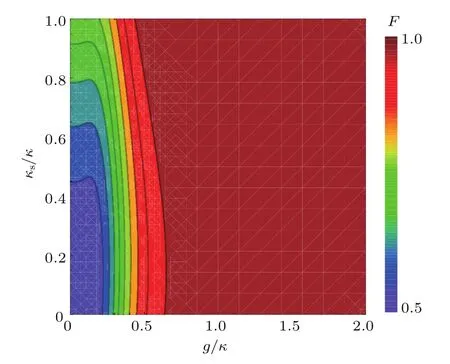
图4 (网刊彩色)保真度随耦合强度和腔泄漏的变化(这里,选择|α−β|=1)Fig.4.(color online)The curve of fi delity vs coupling strength and cavity leakage.Here,|α−β|=1.

从图4可以看出,F的最小值为0.5.在弱耦合条件(g/κ＜0.5)下,F的值较小,而且受腔泄漏的影响非常大.而在腔强耦合条件(g/κ＞0.5)下,F接近于1,而且可以保持稳定,几乎不受腔泄漏的影响.弱耦合g/κ=0.3的情况下,当κs/κ=0时,成功概率F=66.34%.强耦合g/κ=1.5条件下,当κs/κ=0时,F=99.81%.当g/κ=2.4时,相对于κs/κ=0或0.1,F=99.97%或者99.86%.当g/κ＞0.7时,F趋于稳定,不会随着耦合强度和泄漏率的增加有太大的变化.所以本文的纠缠浓缩方案对腔的边泄漏率要求不高,而且只要满足g/κ＞0.7,继续增加耦合强度也没有实际意义.系统的耦合强度取决于带电激子的振荡强度和微腔的模体积,量子点和光学微腔的弱耦合在实验室比较容易实现,强耦合实现起来虽有一些难度,但近年来也取得了很大进展.在直径d=1.5µm的微柱形光学微腔中,g≃0.5(κ+κs)的耦合强度已经实现[33],对应的腔品质因子Q=8800.当腔的直径d=2µm时,其品质因子可以达到Q=4×104[34],通过改善样品的设计和制备方法,耦合强度可以达到g≃2.4(κ+κs)[35].现有的条件已经可以满足实验的要求,本文的方案是可行的.

5 结 论

本文利用两个微腔中的量子点和一个光子作为辅助,实现了光子偏振非最大纠缠态的浓缩,得到了最大纠缠态.首先,利用光开关让辅助光子a和光子A依次与第一个量子点相互作用,再将光子a通过两个可能的通道传送给第二个参与者,以确保光子a的量子态不受通道噪声的影响;然后让光子a和B依次与第二个量子点相互作用;最后对两个量子点的自旋态和辅助光子的偏振态进行测量,根据测量结果对光子对AB执行相应的操作即可得到最大的偏振纠缠态.在不考虑腔边泄漏的理想情况下,方案的成功概率为1. 本文也以|R〉1|↑〉s1|↑〉s2的测量结果为例计算了方案的保真度,结果显示本文的纠缠浓缩方案在耦合强度g/κ＞0.7时可以达到99.8%以上,而且受腔泄漏的影响也很小.在实际的量子通信过程中,要得到初始纠缠态的系数信息,需要两个参与者可对足够数量光子对进行测量,这样消耗大量的纠缠资源.本文的纠缠浓缩方案中,初始纠缠态的系数影响很小,可以忽略,这就避免了纠缠资源的浪费.而且本方案不需要重复执行,大大简化了纠缠浓缩的过程.这些特点都增加了纠缠浓缩的通用性和效率,进而保证了量子纠缠态的品质.量子纠缠浓缩可以在一定程度上消除消相干作用造成的纠缠态品质下降,使得两个参与者共享的是最大纠缠态,这在远距离量子通信中是非常有用的,可以提高量子隐形传送、量子密钥分配、量子密码学等方案的安全性.量子纠缠浓缩在可容错量子计算和分布式量子计算中也有着极其重要的应用.

[1]Bennett C H,Bernstein H J,Popescu S,Schumacher B 1996Phys.Rev.A53 2046

[2]Guo R,Zhou L,Gu S P,Wang X F,Sheng Y B 2016Chin.Phys.B25 030302

[3]Zhang W Z,Li W D,Shi P,Gu Y J 2011Acta Phys.Sin.60 060303(in Chinese)[张闻钊,李文东,史鹏,顾永建2011物理学报60 060303]

[4]Zhou L,Wang D D,Wang X F,Gu S F,Sheng Y B 2017Chin.Phys.B26 020302

[5]Zhao Z,Pan J W,Zhan M S 2001Phys.Rev.A64 014301

[6]Yamamoto T,Koashi M,Imoto N 2001Phys.Rev.A64 012304

[7]Bose S,Vedral V,Knight P L 1999Phys.Rev.A60 194

[8]Sheng Y B,Deng F G,Zhou H Y 2008Phys.Rev.A77 062325

[9]Sheng Y B,Zhou L,Zhao S M,Zheng B Y 2012Phys.Rev.A85 012307

[10]Ding S P,Zhou L,Gu S P,Wang X F,Sheng Y B 2017Int.J.Theor.Phys.56 1912

[11]Qu C C,Zhou L,Sheng Y B 2015Quant.Inf.Process.14 4131

[12]Fei S M 2016Sci.China:Inform.Sci.59 128501

[13]Song T T,Tan X,Wang T 2017Sci.Rep.7 1982

[14]Ren B C,Du F F,Deng F G 2013Phys.Rev.A88 012302

[15]Cao C,Wang T J,Mi S C,Zhang R,Wang C 2016Ann.Phys.369 128

[16]Du F F,Deng F G,Long G L 2016Sci.Rep.6 35922

[17]Loss D,DiVincenzo D P 1998Phys.Rev.A57 120

[18]Wei H R,Deng F G 2013Opt.Express21 17671

[19]Chen Q C 2016Acta Phys.Sin.65 247801(in Chinese)[陈秋成 2016物理学报65 247801]

[20]Wang S X,Li Y X,Wang N,Liu J J 2016Acta Phys.Sin.65 137302(in Chinese)[王素新,李玉现,王宁,刘建军2016物理学报65 137302]

[21]Wei H R,Deng F G 2013Phys.Rev.A87 022305

[22]Senellart P,Solomon G,White A 2017Nat.Nanotechnol.12 1026

[23]Ren B C,Deng F G 2014Sci.Rep.4 4623

[24]Shimizu H,Saravanan S,Yoshida J,Ibe S,Yokouchi N 2006Appl.Phys.Lett.88 241117

[25]Ulbrich N,Bauer J,Scarpa G,Boy R,Schuh G,Abstreiter G,Schmult S,Wegscheider W 2003Appl.Phys.Lett.83 1530

[26]Wang C,Zhang Y,Jin G S 2011Phys.Rev.A84 032307

[27]Wang C 2012Phys.Rev.A86 012323

[28]Sheng Y B,Zhou L,Wang L,Zhao S M 2013Quant.Inf.Process.12 1885

[29]Ren B C,Long G L 2014Opt.Express22 6547

[30]Scully M O,Zubairy M S 1997Quantum Optics(Cambridge:Cambridge University Press)

[31]Hu C Y,Munro W J,O’Brien J L,Rarity J G 2009Phys.Rev.B80 205326

[32]Bonato C,Haupt F,Oemrawsingh S S R,Gudat J,Ding D,van Exter M P,Bouwmeester D 2010Phys.Rev.Lett.104 160503

[33]Reithmaier J P,Se¸k G,Löラer A,Hofmann C,Kuhn S,Reitzenstein S,Keldysh L V,Kulakocskii V D,Reinecke T K,Forchel A 2004Nature432 197

[34]Yoshie T,Scherer A,Hendrickson J,Khitrova G,Gibbs H M,Rupper G,Ell C,Shchekin O B,Deppe D G 2004Nature432 200

[35]Reitzenstein S,Hofmann C,Gorbunov A,Strauß M,Kwon S H,Schneider C,Löラer A,Hö fl ing S,Kamp M,Forchel A 2007Appl.Phys.Lett.90 251109