高斯切趾型光纤布拉格光栅外腔半导体激光器的混沌输出特性∗

起俊丰 钟祝强 王广娜 夏光琼 吴正茂

(西南大学物理科学与技术学院,重庆 400715)

(2017年7月23日收到;2017年8月20日收到修改稿)

1 引 言

半导体激光器(SL)因其体积小、制造成本低、可直接调制等优点被广泛应用于光通信、光存储、光互连等领域[1−3].SL作为一种非线性器件,在受到光反馈、光注入和光电反馈等外部扰动时可以表现出丰富的非线性动力学行为[4−10].其中,光反馈SL因其具有结构相对简单、易于调控且能够产生高维度光混沌信号等特点,从而在高速光混沌保密通信、物理随机数获取、光混沌雷达等应用领域中受到极大关注[11−18].然而,光在外腔中的往返过程势必会导致外腔反馈SL混沌输出中包含较明显的延时特征(TDS),而这种混沌TDS不利于混沌信号在相关领域的应用.例如,在高速光混沌保密通信中[11],窃密者可利用非线性时间序列分析技术识别并提取SL混沌输出的TDS,进而确定光反馈SL的关键系统参量——反馈时间,借助反馈时间信息对混沌信号进行相空间重构[19],从而导致通信的安全性受到威胁;在基于混沌熵源获取物理随机数的应用中[15],如果光反馈SL输出的混沌信号具有明显TDS,这将导致所获得的物理随机数的统计性能劣化;而在光混沌雷达应用中[18],混沌信号的TDS会导致相关曲线呈现明显的旁瓣,这将有可能引起光混沌雷达对探测目标的误判.因此,对光反馈SL混沌输出的TDS进行抑制具有重要意义.

近年来,已有一些对光反馈SL混沌输出TDS进行抑制的相关报道[20−34].例如,Lee等[20]在光反馈SL混沌系统中增加另一个腔而形成双外腔反馈系统结构,实验获得的光混沌信号的TDS被有效抑制.Rontani等[21]理论研究了单外腔反馈SL系统输出的混沌TDS,结果表明,当反馈强度较小且外腔反馈时间接近SL弛豫振荡周期时,单外腔反馈SL混沌输出的TDS能够被较好抑制.上海交通大学义理林教授课题组通过引入色散补偿单元[22]、太原理工大学张建忠等利用布里渊散射技术[23]均在外腔反馈SL混沌输出的TDS抑制方面取得了良好效果.本课题组理论和实验研究了双外腔反馈SL系统混沌输出的TDS,给出了混沌信号TDS被抑制的所需参数范围[24].此外,针对光反馈作用下的垂直腔面发射激光器(VCSEL),也相继报道了一些抑制混沌信号TDS的方案[25−27].除了TDS,混沌带宽是评价混沌信号质量的又一个关键指标.一些获取弱TDS、宽带宽混沌信号的方案也相继被提出[28−30].如,Hong等[28]提出将一个VCSEL产生的混沌信号注入到另外一个VCSEL,或采用两个VCSELs互耦方案,实验获得了弱TDS、宽带宽的混沌信号.Cheng等[29]提出并理论证明了通过引入电外差技术可使外腔反馈SL产生的混沌信号的TDS得到有效抑制,同时混沌带宽得到明显增强.Jiang等[30]提出并理论论证了在外腔反馈SL系统中,通过引入一个相位调制器和两个色散单元可获得对TDS抑制较好、带宽明显增强的混沌信号.在上述相关报道中,大多采用平面镜作为SL的外腔,其提供的反馈对波长不具有选择性,即信号中不同频率成分以相同的传输时间反馈回SL中.而对于一些具有滤波特性的反射器件,如法布里-珀罗干涉仪或光纤布拉格光栅(FBG),其提供波长选择性的光反馈使不同频率光经过不同的群延时被反馈回SL,这将更利于混沌信号TDS的抑制[31−34].Li等[31,32]利用均匀FBG替代普通平面镜构成FBG反馈SL(FBGF-SL),理论与实验证实了在特定的参数范围内可获得比采用平面镜作为反射腔时对TDS抑制更好、混沌带宽更宽的混沌信号.Wang等[34]采用啁啾FBG作为外腔反射镜,理论及实验证实了色散反馈能取得较好的TDS抑制效果.已有的研究证明:在相同反射带宽条件下,高斯切趾型光纤布拉格光栅(GAFBG)提供的群延时高于均匀FBG[35].基于此,本文在基于GAFBG反馈SL系统以获取TDS得到更有效抑制的混沌信号方面开展了相关研究.通过分析反馈强度、GAFBG的布拉格频率与SL中心频率之间的频率失谐以及GAFBG特征参量对混沌信号TDS的影响,给出了获取低TDS混沌信号的参数范围;同时,对系统输出的混沌信号带宽随系统参量的变化也进行了分析.

2 理论模型

图1为GAFBG反馈 SL(GAFBGF-SL)混沌系统结构示意图.SL发出的光经中性密度滤波器(NDF)入射到长度为L的GAFBG,经GAFBG反射后再通过NDF反馈回SL.NDF用于控制反馈回路的反馈强度.

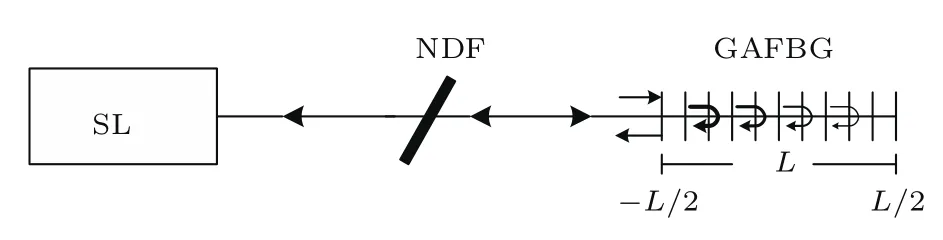
图1 GAFBGF-SL混沌系统结构示意图(SL,半导体激光器;NDF,中性密度滤波器;GAFBG,高斯切趾型光纤布拉格光栅)Fig.1.Schematic diagram of GAFBGF-SL chaotic system.SL,semiconductor laser;NDF,neutral density fi lter;GAFBG,Gaussian apodized fi ber Bragg grating.

对于长度为L的GAFBG(如图1所示),在z方向上的折射率分布为[35]

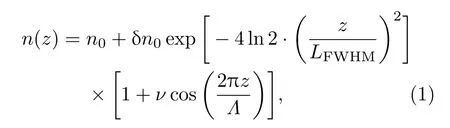
式中,δn0·exp[−4ln2·(z/LFWHM)2]表示在z方向上的“直流”折射率改变δn(z),n0为纤芯原折射率,ν是折射率改变的条纹可见度,光栅周期Λ=λB/(2n0),λB为光栅的布拉格波长,δn0是“直流”折射率改变的最大值,LFWHM为光栅折射率剖面的半极大值全宽度;z∈(−L/2,L/2),z=−L/2对应光栅的入射端面,z=0对应光栅的中心.

GAFBG的反射频率响应可采用分段法进行计算.将GAFBG分成M段,其中每段可视为一均匀FBG.基于传输矩阵法可得在入射界面处前向传播(+z方向)和后向传播(−z方向)波的振幅RM和SM为

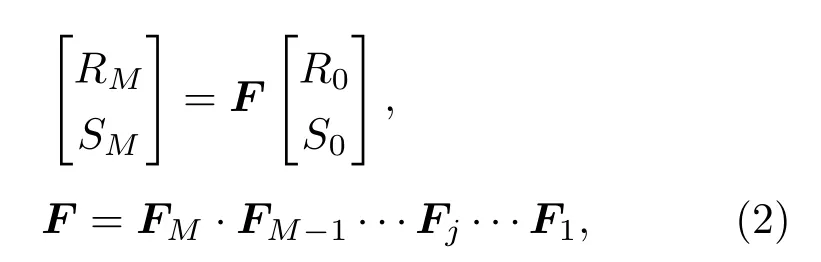
式中矩阵Fj为

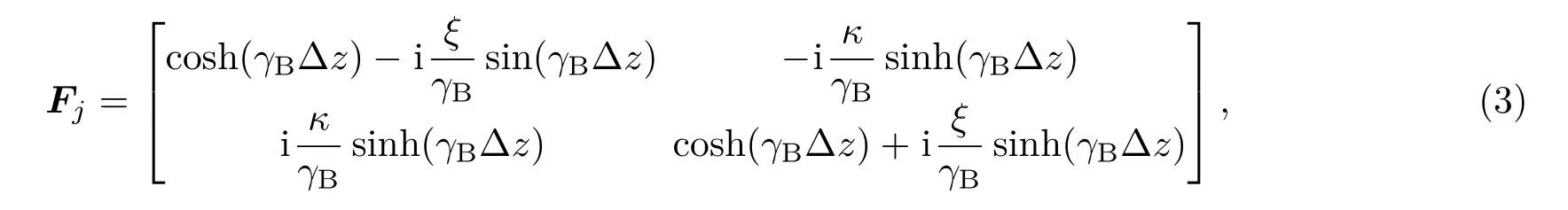
其中,Δz表示第j段的长度;γB定义为

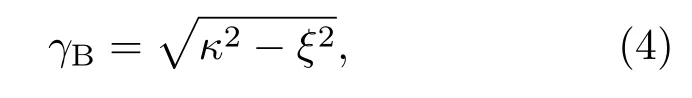
κ= πνδn(z)/λ为第j段的“交流”耦合系数,ξ=δ+σ为第j段的“直流”自耦合系数,模式间的失谐δ=n(z)(Ω−ΩB)/c(ΩB=2πc/λB为光栅的布拉格角频率,c是真空中的光速),“直流”耦合系数σ=Ωδn(z)/c.假设边界条件R0=R(L/2)=1,S0=S(L/2)=0,可由SM/RM求得GAFBG的反射频率响应r(Ω),强度反射率ρ=|r(Ω)|2.

基于光反馈SL的Lang-Kobayashi模型,并考虑GAFBG的特性,描述GAFBGF-SL的速率方程组为[31,32]

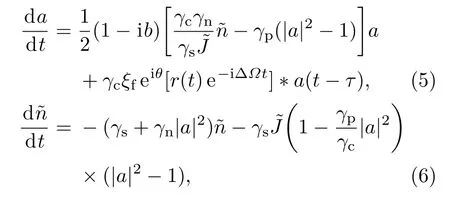
上述方程组中,a(t)是归一化光场复振幅,˜n(t)是归一化载流子密度,b是线宽增强因子,γc是腔衰减率,γs是自发载流子弛豫速率,γn是微分载流子弛豫速率,γp是非线性载流子弛豫速率,˜J是归一化偏置电流,ξf是归一化反馈强度,τ是反馈延时,θ是反馈光相位;角频率失谐ΔΩ=2πΔf,(Δf=fB−f0,其中fB=ΩB/(2π)为GAFBG布拉格频率,f0是SL中心频率),∗表示卷积;r(t)是GAFBG的脉冲响应,为GAFBG反射频率响应r(Ω)的逆傅里叶变换.

采用自相关(SF)[21]、互信息[21]、排列熵[36]等多种方法可以对时滞系统的TDS进行评估.本文采用SF来评估系统的TDS.SF定义为[21]

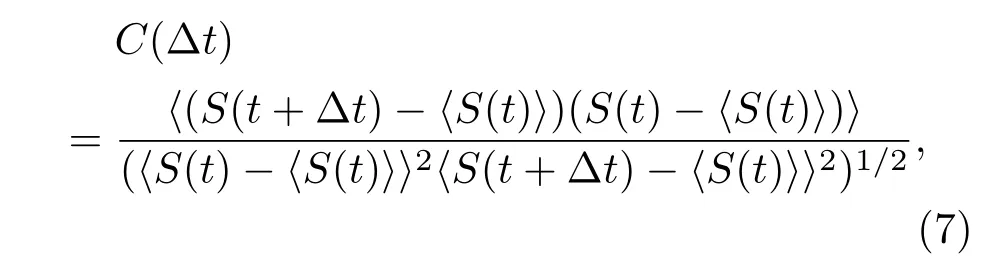
式中,S(t)表征输出强度时间序列,〈·〉表示时间平均值,Δt表示时移.SF的峰值以及峰值所在位置呈现了输出信号的TDS.

3 结果与讨论

利用四阶Runge-Kutta方法对(5)和(6)式进行数值求解,数值求解中所用参数如下[32]:b=3.2,γc=5.36×1011s−1,γs=5.96×109s−1,γn=7.53×109s−1,γp=1.91×1010s−1,˜J=1.222.对于GAFBG反馈,L=6 cm,n0=1.45,λB=1550 nm,ν=1,M=100,τ=5 ns,θ=0 rad,LFWHM=L/3.

3.1 GAFBGF-SL非线性动力学特性

首先分析ξf取不同值时GAFBGF-SL的动力学特性. 图2给出了δn0=1.5×10−4,Δf=8 GHz,ξf取不同值时GAFBGF-SL输出的部分典型状态的时间序列、功率谱和相图.当ξf=0.003时(如图2(a)),GAFBG提供的反馈较弱,SL输出处于稳(S)态,功率谱峰值出现在10.25 GHz,对应激光器的弛豫振荡频率;当ξf=0.017时(如图2(b)),在时间序列中观察到强度峰值形成的慢变包络,功率谱中出现了除弛豫振荡频率外许多其他频率成分,相图中可以观察到多个环,表明此时系统处于准周期(QP)态;当ξf=0.030时(如图2(c)),时间序列呈现无规则振荡,功率谱主峰依然出现在激光器的弛豫振荡频率附近,但谱明显展宽且变得光滑,相图表现为奇怪吸引子,表明此时系统处于混沌(CO)态.

为了更清晰地呈现GAFBGF-SL随ξf改变时的动力学演化路径,图3给出了δn0=1.5×10−4,Δf=8 GHz时GAFBGF-SL输出的时间序列极值随ξf改变的分岔图,其中图3(a),(b),(c)三个工作点分别对应图2(a),(b),(c)的情形.如图3所示,当ξf较小(ξf＜0.015)时,GAFBGF-SL输出时间序列的极值是一个稳定值,此时GAFBGF-SL处于S态;当ξf位于工作点(b)附近时,出现了多个强度极值,此时GAFBGF-SL处于QP态;进一步增大ξf,GAFBGF-SL输出时间序列的极值点个数明显增加,GAFBGF-SL进入CO态.下面重点研究当GAFBGF-SL处于CO态时,系统输出混沌信号的特性.

3.2 反馈强度与频率失谐对GAFBGF-SL输出混沌信号TDS和带宽的影响

图2 δn0=1.5×10−4,Δf=8 GHz时,GAFBGF-SL输出的时间序列(第一列)、功率谱(第二列)以及相图(第三列),其中反馈强度ξf分别为(a)0.003,(b)0.017,(c)0.030Fig.2.Time-series(the fi rst column),power spectra(the second column)and phase portraits(the third column)of the output from GAFBGF-SL with different feedback strengths ξf= (a)0.003,(b)0.017,(c)0.030 under δn0=1.5 × 10−4and Δf=8 GHz.

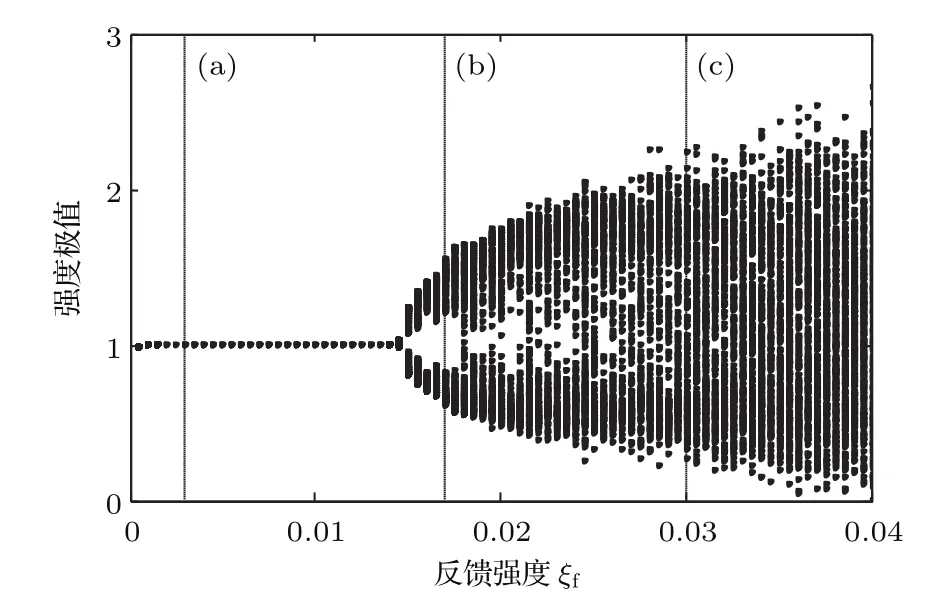
图3 当δn0=1.5×10−4,Δf=8 GHz时,GAFBGFSL输出时间序列极值随ξf变化的分岔图Fig.3.Bifurcation diagram of the output intensity extremes from the GAFBGF-SL with the vary of ξf under δn0=1.5 × 10−4and Δf=8 GHz.

由于GAFBG的反射具有波长选择性,因此可以预计GAFBG的布拉格频率与SL中心频率之间的频率失谐Δf对GAFBGF-SL混沌输出的TDS影响较大.图4给出了GAFBG的反射谱(蓝色)和群延时(红色)(第一列),GAFBGF-SL混沌输出的光谱(第二列)、功率谱(第三列)以及SF曲线(第四列),其中频率失谐Δf分别为(a)−10 GHz,(b)14 GHz,(c)36 GHz,图中频率偏移是相对于自由运行激光器的中心频率而言.当Δf=−10 GHz时,如图4(a1)所示,GAFBG在自由运行SL的中心波长处提供的反射率很小,因此SL的中心波长的红移现象并不明显,而在GAFBG的反射带宽内,由于GAFBG所提供的反馈导致GAFBGFSL输出的光谱在这个范围内得到明显增强,从而出现如图4(a2)的光谱分布.此时功率谱连续(图4(a3)),说明GAFBGF-SL处于CO态.通过仔细观察GAFBGF-SL输出的功率谱,可发现一些等间隔峰,其间隔频率约为GAFBGF-SL外腔反馈时间的倒数,而输出时间序列的SF曲线(图4(a4))在Δt≈τ附近有一个较明显的特征峰,其峰值为0.126.当Δf=14 GHz时,如图4(b1)所示,此时SL自由运行的中心频率处于GAFBG反射谱主瓣内,GAFBG提供强的反射率导致SL的输出的峰值波长发生较强的红移,频率偏移量为−18.0 GHz(如图4(b2)所示).功率谱中等间隔峰的结构更加明显,时间序列的SF曲线在Δt≈τ附近的峰值增大到0.226.当Δf=36 GHz时,SL自由运行的中心频率处于GAFBG反射谱主瓣低频边缘(图4(c1)),GAFBG提供的反馈较小,SL中心波长红移不明显,且此时光谱中的主要能量集中于GAFBG反射谱主瓣边缘、群延时达到极值的附近,从而导致GAFBGF-SL输出的功率谱几乎观测不到等间隔峰结构,输出时间序列的SF曲线在Δt≈τ附近也没有明显的特征峰,最大值仅为0.019.从上述结果可以看出,GAFBGF-SL输出混沌信号的TDS取决于GAFBG对不同频率处提供的反馈强度的大小以及群延时.

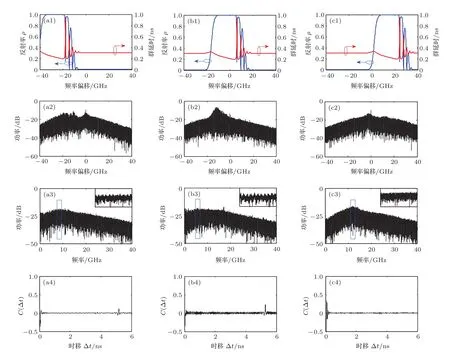
图4 (网刊彩色)ξf=0.11,δn0=1.5×10−4时,GAFBG 的反射谱(蓝色)和群延时(红色)(第一排)、GAFBGF-SL混沌输出的光谱(第二排)、功率谱(第三排)以及SF曲线(第四排);频率失谐Δf分别为(a)−10 GHz,(b)14 GHz,(c)36 GHz;频率偏移是相对于自由运行SL中心频率的偏移Fig.4.(color online)Re fl ectivity spectra(blue)and group delay(red)of GAFBG(the fi rst row),optical spectra(the second row),power spectra(the third row),and SF curves(the fourth row)of the GAFBGF-SL chaotic output,where ξf=0.11, δn0=1.5 × 10−4and Δf=(a) −10 GHz,(b)14 GHz,and(c)36 GHz,and frequency offset is to the free-running SL.

对于混沌信号在相关领域的应用而言,通常不仅要求混沌信号的TDS比较弱,同时其混沌带宽应该比较宽.因此,有必要结合混沌信号的TDS以及混沌带宽随系统参数的演化情况,确定获取满足要求的混沌信号所需的系统参数范围.混沌输出的TDS强弱可用SF曲线在时移Δt∈[4 ns,6 ns]内的最大值σt表征,σt越大说明GAFBGF-SL输出混沌信号的TDS越明显;而GAFBGF-SL输出信号的带宽可利用文献[37]中的有效带宽(EWB)来定量描述.图5给出了δn0取不同值时,GAFBGFSL输出的混沌信号的σt(第一列)和EWB(第二列)在ξf和Δf构成的参量空间的演化、以及相应的GAFBG的反射谱(蓝线)和群延时(红线)(第三列).如前所述,δn0表示GAFBG “直流”折射率改变的最大值,它决定GAFBG的反射带宽.如第三列所示,当δn0=1.0×10−4,1.5×10−4和3.0×10−4时,GAFBG的带宽分别为13.3,20.3,40.4 GHz.在TDS特征峰值σt的演化图(第一列)中,红色区域表示σt值相对较大,而蓝色区域表示σt值相对较小.通过仔细考察TDS得到较好抑制的区域(σt＜0.1),发现在这些区域GAFBGF-SL的输出光谱位于GAFBG反射谱主瓣低频边缘、群延时出现极大值的附近;随着GAFBG的带宽增大,GAFBGF-SL输出的混沌信号的TDS得到较好抑制的参数区域相应增大.在EBW的演化图(第二列)中,深蓝色区域表示GAFBGF-SL输出的EBW 值较小(＜10 GHz),根据文献[37]可知此时GAFBGF-SL输出处于S态或周期振荡态.EBW的演化规律与TDS的演化规律相似,结合σt及EBW在ξf和Δf构成的参数空间下的演化图,能够确定产生弱TDS、宽带宽混沌信号的所需的参数范围.

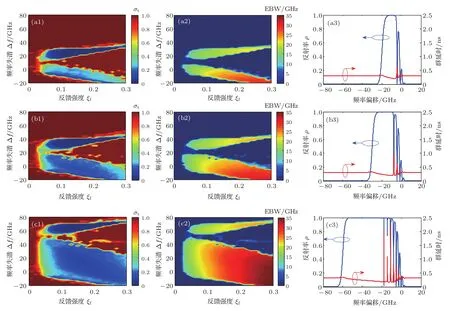
图5 (网刊彩色)(a)δn0=1.0×10−4,(b)1.5×10−4,(c)3.0×10−4时GAFBGF-SL输出的TDS特征峰值σt(第一列)、有效带宽(第二列)在ξf和Δf构成的参数空间的演化图以及GAFBG的反射谱(蓝线)和群延时(红线)(第三列);此处频率偏移是相对于GAFBG的布拉格频率的偏移Fig.5.(color online)Maps of the characteristic peak value of TDS(the fi rst column)and effective bandwidth EBW(the second column)of the GAFBGF-SL output in the parameter space of ξfand Δf,and the re fl ectivity spectra(blue lines)and group delays(red lines)of the GAFBG(the third column)with frequency offset to the Bragg frequency of FBG under δn0=(a)1.0×10−4,(b)1.5×10−4,and(c)3.0×10−4.

4 结 论

本文基于光反馈SL的速率方程模型,数值仿真了GAFBGF-SL动力学行为,并对GAFBGF-SL输出信号的TDS以及EBW进行了分析.仿真结果表明:随反馈强度的增加,GAFBGF-SL可表现出由S态、QP态进入CO态的动力学演化路径;反馈强度ξf和频率失谐Δf显著影响系统混沌输出的TDS以及EBW;通过绘制GAFBGF-SL系统输出的TDS和EBW在ξf和Δf构成的参量空间下的分布图,可确定获取弱TDS、宽带宽混沌信号的参数范围.

[1]Lin C F,Su Y S,Wu B R 2002IEEE Photon.Technol.Lett.14 3

[2]Sakaguchi J,Katayama T,Kawaguchi H 2010Opt.Express18 12362

[3]Augustin L M,Smalbrugge E,Choquette K D,Karouta F,Strijbos R C,Verschaffelt G,Geluk E J,van de Roer T G,Thienpont H 2004IEEE Photon.Technol.Lett.16 708

[4]Mork J,Tromborg B,Mark J 1992IEEE J.Quantum Electron.28 93

[5]Yan J,Pan W,Li N Q,Zhang L Y,Liu Q X 2016Acta Phys.Sin.65 204203(in Chinese)[阎娟,潘炜,李念强,张力月,刘庆喜2016物理学报65 204203]

[6]Hwang S K,Liu J M 2000Opt.Commun.183 195

[7]Zhang L Y,Pan W,Yan L S,Luo B,Zou X H,Xiang S Y,Li N Q 2012IEEE Photon.Technol.Lett.24 1693

[8]Yan S L 2016Chin.Phys.B25 090504

[9]Lin F Y,Liu J M 2003Opt.Commun.221 173

[10]Zhong D Z,Luo W,Xu G L 2016Chin.Phys.B25 094202

[11]Argyris A,Syvridis D,Larger L,Annovazzi-Lodi V,Colet P,Fischer I,García-Ojalvo J,Mirasso C R,Pesquera L,Shore K A 2005Nature438 343

[12]Zhong D Z,Deng T,Zheng G L 2014Acta Phys.Sin.63 070504(in Chinese)[钟东洲,邓涛,郑国梁 2014物理学报63 070504]

[13]Li N Q,Pan W,Luo B,Yan L S,Zou X H,Jiang N,Xiang S Y 2012IEEE Photon.Technol.Lett.24 1072

[14]Liu J,Wu Z M,Xia G Q 2009Opt.Express17 12619

[15]Uchida A,Amano K,Inoue M,Hirano K,Naito S,Someya H,Oowada I,Kurashige T,Shiki M,Yoshimori S,Yoshimura K,Davis P 2008Nat.Photon.2 728

[16]Kanter I,Aviad Y,Reidler I,Cohen E,Rosenbluh M 2010Nat.Photon.4 58

[17]Li X Z,Li S S,Zhuang J P,Chan S C 2015Opt.Lett.40 3970

[18]Lin F Y,Liu J M 2004IEEE J.Sel.Top.Quantum Electron.10 991

[19]Prokhorov M D,Ponomarenko V I,Karavaev A S,Bezruchko B P 2005Physica D203 209

[20]Lee M W,Rees P,Shore K A,Ortin S,Pesquera L,Valle A 2005IEE Proc.Optoelectron.152 97

[21]Rontani D,Locquet A,Sciamanna M,Citrin D S 2007Opt.Lett.32 2960

[22]Ke J X,Yi L L,Hou T T,Hu Y,Xia G Q,Hu W S 2017IEEE Photon.J.9 7200808

[23]Zhang J Z,Feng C K,Zhang M J,Liu Y,Zhang Y N 2017IEEE Photon.J.9 1502408

[24]Wu J G,Xia G Q,Wu Z M 2009Opt.Express17 20124

[25]Xiang S Y,Pan W,Luo B,Yan L S,Zou X H,Jiang N,Yang L,Zhu H N 2011Opt.Commun.284 5758

[26]Lin H,Hong Y H,Shore K A 2014J.Lightwave Technol.32 1829

[27]Xiao P,Wu Z M,Wu J G,Jiang L,Deng T,Tang X,Fan L,Xia G Q 2013Opt.Commun.286 339

[28]Hong Y H,Spencer P S,Shore K A 2014IEEE J.Quantum Electron.50 236

[29]Cheng C H,Chen Y C,Lin F Y 2015Opt.Express23 2308

[30]Jiang N,Wang C,Xue C P,Li G L,Lin S Q,Qiu K 2017Opt.Express25 14359

[31]Li S S,Liu Q,Chan S C 2012IEEE Photon.J.4 1930

[32]Li S S,Chan S C 2015IEEE J.Sel.Top.Quantum Electron.21 541

[33]Zhong Z Q,Li S S,Chan S C,Xia G Q,Wu Z M 2015Opt.Express23 15459

[34]Wang D M,Wang L S,Zhao T,Gao H,Wang Y C,Chen X F,Wang A B 2017Opt.Express25 10911

[35]Erdogan T 1997IEEE J.Lightwave Technol.15 1277

[36]Bandt C,Pompe B 2002Phys.Rev.Lett.88 174102

[37]Lin F Y,Chao Y K,Wu T C 2012IEEE J.Quantum Electron.48 1010