扭转形变对石墨烯吸附O原子电学和光学性质影响的电子理论研究∗

范达志 刘贵立 卫琳

(沈阳工业大学建筑工程学院,沈阳 110870)

(2017年7月3日收到;2017年9月6日收到修改稿)

1 引 言

表面科学中一个很重要的课题是原子、分子与材料表面的相互作用.因为原子、分子的表面吸附影响了材料的稳定性以及材料的光学、电学性质,这些变化的本质原因是吸附、吸附物影响了衬底的几何和电子结构.

2004年,石墨烯成功剥离[1,2],其独特的sp2杂化成键方式使其具有诸多特殊性质.比如,异常的量子霍尔效应[3]、电子迁移率[4]、宽频的光吸收以及无质量的狄拉克费米子[5]等.这些奇特的物理特性,使其成为当今凝聚态物理研究的热点.二维的平面结构使其拥有极大的比表面积,提高了石墨烯对原子、分子吸附的灵敏度,因此对石墨烯吸附的研究意义重大.最近研究发现,导电性良好的石墨烯在燃料电池方面比其他碳纳米材料[6,7]更有优势,成为当前电极材料极好的选择,因而对燃料电池氧化还原反应的中间产物O原子与石墨烯电极间的相互作用进行研究十分必要.孙建平等[8]通过第一性原理研究了掺杂石墨烯吸附燃料电池中间产物O原子等的吸附能、态密度以及电子转移,结果表明掺杂可以提高石墨烯对O原子的吸附能,提高催化能力.单层无缺陷石墨烯在金属腐蚀防范领域具有巨大的应用潜力,而研究都集中在实验方面[9,10],而且石墨烯长期浸泡,使得其发生电化学反应会加速金属腐蚀.可见,在理论上了解主要腐蚀因子O原子与石墨烯的机理相当必要.近日,Zhou等[11]通过第一性原理研究了O原子吸附对石墨烯电子结构与光学性能的影响,发现O原子的吸附对石墨烯电子结构影响很大,使其由准金属变成了半导体,覆盖度的改变对带隙也有影响.在光学性能方面,O原子的吸附降低了其对光的吸收系数和反射率.显然,O原子吸附于石墨烯并对其性能的影响不容忽视.

单层石墨烯的有效厚度只有0.07 nm,所以极易发生几何形变,特别对一个已存在表面波纹的或自由直立的石墨烯,变形很容易发生[12],而且其电子特性对形变极其敏感[13,14].根据鲍林的杂化轨道理论,我们可以这样认为:石墨烯碳原子所具有的sp2杂化状态是由一个2s轨道和两个2p轨道2px及2py混合而成,并且三种状态的概率分布完全等价,形成σ键;没有参加sp2杂化的第四个2p轨道2pz,在垂直于XOY平面的Z轴上呈“哑铃”状,这些互相平行的2p轨道彼此连贯重叠形成离域的π键;当石墨烯平面发生形变时,轨道不再保持互相平行,使得σ-π轨道之间再杂化,进而导致不同方向上的键长发生变化.这是扭转变形使石墨烯电子结构改变的关键.李骏等[15]在纳米带扭曲效应研究中提到σ-π轨道再杂化对电子特性的影响十分明显.

本文基于密度泛函理论(DFT)的第一性原理方法研究了扭转形变对单层石墨烯吸附O原子体系的结构稳定性、电子结构和光学性质,包括吸附能、带隙、吸收系数及反射率的影响.期望这些研究能揭示(有/无)扭转下O原子吸附石墨烯光电特性的物理机制,并为实验提供理论指导.

2 计算方法与模型

本文采用Materials-Studio基于第一性原理的DFT[16]平面赝势的CASTEP模块进行计算.几何优化与计算过程中采用广义梯度近似平面波赝势方法以及Perdew-Burke-Ernzerhof[17]泛函计算电子间的交换关联势.为了减少电子体系展开的平面波基数,采用Vanderbilt超软赝势[18]描述离子实与价电子之间的相互作用,计算时不考虑自旋极化的影响.结构计算中采用Monkhorst-Pack特殊K点取样方法[19],在各模型结构优化中,K点网格取为6×6×1.平面波展开的截止能量取为350 eV,并采用Broyden-Fletcher-Goldfarb-Shanno优化算法[20]进行几何优化,迭代精度收敛值为每个原子的总能量不小于2.0×10−6eV/atom,所有原子力小于0.05 eV/nm,自洽场循环收敛为2.0×10−6eV.计算时取Z方向垂直于石墨烯平面;X,Y平面在石墨烯平面内;真空层厚度取15 Å,此时层间相互作用力可忽略不计.

优化后石墨烯的晶格常数a=0.2465 nm,与实验值[21]的0.246 nm十分接近,本文所有计算均采用此优化值.石墨烯原胞选用4×4×1共32个原子,单胞通过扩建得到本征石墨烯如图1(a),对O原子进行吸附时,考虑三个高对称吸附位:T点,在C原子的正上方;B点,在C—C键的中心;H点,在C原子环中心,如图1(b).对于石墨烯扭转形变的程度,本文用扭转角θ来表征,即4×4×1原胞石墨烯一个边缘相对于另一个边缘转过的角度.具体操作方法:为了便于表述,Zigzag碳原子链被设置成不同的颜色,先将粉色链边缘原子扭转至θ/2,再将黑色链边缘原子朝另一个方向扭转θ/2并固定这两排原子,其他排原子扭转适当角度以便节省优化时间,如图2.

图1 (网刊彩色)石墨烯模型 (a)本征石墨烯模型;(b)石墨烯吸附O原子模型Fig.1.(color online)Graphene model:(a)Intrinsic graphene;(b)O atom absorbed on graphene.

图2 (网刊彩色)扭转模型 (a)正视图;(b)侧视图;(c)俯视图Fig.2.(color online)The torsional mode:(a)The front view;(b)the side view;(c)the top view.

为了研究石墨烯吸附O原子体系在不同扭转角下的结构稳定性,给出吸附能定义式,如下:

其中,Egra为本征石墨烯或扭转石墨烯的能量,EO为O原子的能量,Egra-O为吸附体系的能量.根据(1)式可知,吸附能越大,结构越稳定.

3 结果与讨论

通过对本征石墨烯和石墨烯吸附O原子体系带隙进行试算,结果显示,扭转角在0°—20°时,带隙变化规律最为显著.故下列计算中扭转角取值范围限制在0°—20°,步长取2°.

3.1 结构优化与结构稳定性

采用自动优化的方法,对O原子吸附在三个不同吸附位情况的本征石墨烯进行计算.结果表明,当O原子吸附在C—C键上方时,即B点,体系能量最小,此时结构处于最稳定状态,如图3(a)所示,此结论与文献[11]相一致.通过(1)式计算的吸附能为4.25 eV,与文献[11]的3.97 eV相差不大,距O原子最近的C—C键长为0.151 nm,最近的C—O键长为0.147 nm,与文献[11]相对应的0.152 nm和0.146 nm基本一致.图3(b)为图3(a)的正视图,可见由于O原子与邻近的C原子成键时它们之间的共价相互作用,导致与O原子邻近的C被拔起,使石墨烯结构发生了一定的扭曲.此结论与文献[11]相一致,证明本文参数的选取对石墨烯吸附系统的计算合理可靠.接下来本文的计算都将O原子吸附在石墨烯的桥位.

文献[22]得出,石墨烯扭转角小于150°时,六角蜂窝状结构依然完整.在本文计算过程中,没有发现结构被破坏的情况,而且结构变化不大,所以本文只列出了部分优化后的几何结构,如图4所示.

表1所列为不同扭转角下石墨烯吸附O原子体系的吸附能.受扭转作用体系与未受扭转体系相比,各体系吸附能有所降低.扭转角为10°时,吸附能最低,为3.89 eV,但与未受扭转体系的4.25 eV相差不大.本文的吸附高度定义为O原子与其最近的C的距离,扭转作用对吸附高度影响微弱,扭转角0°—6°时,吸附高度约1.47 Å;扭转角8°—20°时,吸附高度约1.48 Å.

图3 (网刊彩色)石墨烯吸附O原子(B点)优化后几何结构 (a)俯视图;(b)正视图Fig.3.(color online)The structure of O atom absorbed on graphene(B point)after the geometry optimization:(a)The top view;(b)the front view.

图4 (网刊彩色)优化几何模型 (a)–(h)为石墨烯吸附O体系在扭转角2°,8°,14°,20°下的俯视图和正视图Fig.4.(color online)The geometry optimization structure:(a)–(h)The top view and gront view of O atom absorbed graphene with 2°,8°,14°,20° torsion angle.

表1 不同扭转角下石墨烯吸附O原子体系的吸附能Table 1.Adsorption energy of O atom absorbed on graphene system with different torsion angle.

3.2 扭转形变对石墨烯吸附O原子能带结构的影响

采用CASTEP软件对本征石墨烯和石墨烯吸附O原子能带进行计算.结果显示,本征石墨烯在K点能带带隙等于零,如图5(a)所示,为准金属特性,这与理论计算[11,23−25]相一致,并与实验上Varykhalov等[26]和Bao等[27]通过角分辨光发射谱测量的结论符合.石墨烯吸附O原子后,打破了石墨烯的原始对称性,带隙被打开,此处可以理解为由于C原子被拔起使石墨烯平面发生形变,进而导致σ-π轨道的再杂化,使石墨烯由准金属特性变成半导体特性,如图5(b)所示,这一结论与计算结果[11]和实验结果[28]相一致,再次证明本文所选参数可靠.

图6给出了石墨烯吸附O原子体系在0°—20°扭转角下的能带结构,并将带隙值列于表2.为了更好地分析吸附体系带隙的变化,本文同时给出了本征石墨烯受扭下的带隙值,列于表2,两者带隙的变化见图6(l).

从表2可以看出,扭转形变逐渐将本征石墨烯带隙打开,使其变成中等带隙半导体,这是典型的σ-π轨道再杂化对电子结构的影响,而且变形可以打开带隙的相关实验[29−31]早有报道.扭转角为0°—6°时,带隙增长较慢且不到0.1 eV,始终对应准金属;扭转角为8°和10°时,带隙分别为0.12 eV和0.17 eV,为小带隙半导体;扭转角为12°时,带隙为0.24 eV,对应中等带隙半导体.当扭转角继续增大,直到18°时,带隙值基本没有变化,保持在0.3 eV,为中等带隙半导体;扭转角为20°时,带隙从18°的0.31 eV降低到0.2 eV,变化较大.

扭转对本征石墨烯带隙影响较大,那么石墨烯吸附O原子体系带隙会发生怎样的变化呢?这是个有趣的问题.图6和表2显示,扭转角为12°的吸附体系带隙为间接带隙,其他吸附体系都为直接带隙.不加扭转形变的石墨烯吸附O原子体系带隙为0.12 eV,为小带隙半导体.对其施加扭转形变以后,能带结构和带隙都发生了变化,带隙随扭转角的增大呈先减小再趋于稳定后又增加的趋势.扭转角为2°—8°时,有一个非常小的带隙,对应准金属;扭转角为10°—16°时,带隙稳定在0.11 eV左右,对应窄带隙半导体;扭转角为18°时,带隙增大为0.16 eV;扭转角为20°时,带隙进一步打开,达到0.22 eV,对应中等带隙半导体.

从图6(l)可以看出:扭转角在0°—4°范围内,吸附体系带隙高于本征体系带隙,并在4°时两体系带隙相等;扭转角在4°—18°范围内,吸附体系低于本征体系带隙,其中在10°—16°范围内本征体系带隙呈线性增长而吸附体系带隙基本保持不变;扭转角为20°时,吸附体系带隙再次超过本征体系带隙.

图5 (a)本征石墨烯能带;(b)石墨烯吸附O原子能带Fig.5.(a)The band structure of intrinsic graphene;(b)the band structure of O atom absorbed on graphene.

表2 本征石墨烯和石墨烯吸附O原子在不同扭转角下的带隙值Table 2.The band gaps of intrinsic graphene and O atom adsorbed on graphene with different torsion angle.

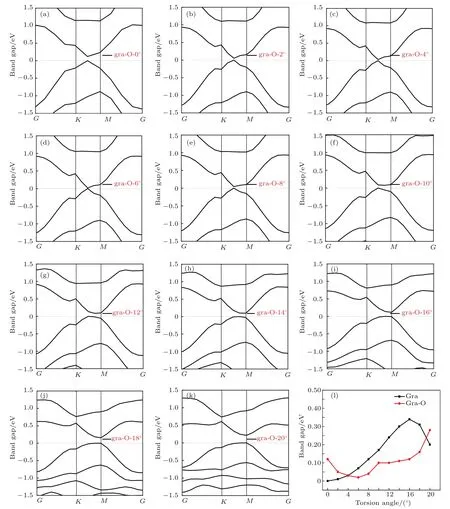
图6 (a)–(k) 分别为石墨烯吸附O原子体系在扭转角0°,2°,4°,6°,8°,10°,12°,14°,16°,18°,20° 下的能带结构;(l) 为本征石墨烯(黑线)和石墨烯吸附O原子(红线)随扭转角的变化Fig.6.(a)–(k)The band structure of O atom adsorbed on graphene with 0°,2°,4°,6°,8°,10°,12°,14°,16°,18°,20°torsion angle;(l)the band gap of intrinsic and O atom absorbed on graphene changes with torsion angle.

3.3 扭转形变对石墨烯吸附O原子光学性质的影响

吸收谱定义为电磁波在通过某介质时能量的衰减;反射谱定义为反射波振幅与入射波振幅之比,即某一种晶体如果强烈吸收某一光谱范围的光,它就能有效地反射在同一光谱范围内的光.本文计算了石墨烯吸附O原子体系的吸附系数和反射率,如图7所示.

从图7(a)可以看出,所有体系在波长约278 nm处出现一个吸收峰,随着波长的增大,所有体系的光吸收系数均降低.波长大于约890 nm时,扭转角为12°的吸附体系的光吸收系数明显高于其他吸附体系.扭转角为18°的吸附体系在波长7750 nm处停止对光的吸收,其他吸附体系在波长约为7486 nm处停止对光的吸收.从图7(b)可以看出,所有吸附体系在波长约为40 nm处开始对光有吸收,同时,吸收系数的增长速度随扭转角的增大而增大.从图7(c)可以看出,在吸收峰处,扭转形变使所有吸附体系光吸收系数降低,随着扭转作用的增强,吸收峰值按照扭转角0°,2°,4°,6°,18°,8°,20°,10°,12°,16°,14°的顺序依次降低. 与扭转角为0°的体系相比,扭转作用使扭转角2°—12°吸附体系的吸收峰发生红移,并使扭转角14°—20°的吸附体系吸收峰发生蓝移.吸收峰的红移和蓝移可能是由于在持续扭转中结构形变引发的能带变化导致的.O原子的吸附将C原子拔起,C—C键变长,在比较小的扭转角度,随着扭转角的增加,C—C键长先逐渐减少,增强了电子的相互作用,拓展了带宽,从而导致了吸收峰的红移,并且吸收峰值随着角度的增加而减少;但是当扭转角再持续增加时,C—C键长又明显变长,这样就会削弱C—C的相互作用,使得电子能级变得孤立,从而使得吸收峰蓝移,峰值增加.从带隙的变化中看到了相似的变化规律,带隙先随着扭转的增加而减少,随后又逐渐增加,这和吸收峰处波长先增大后减小的规律也是一致的.同时,本文又将带隙打开明显的体系的带隙值和根据截止波长计算的截止吸收能量进行了对比,见表3.从表3可以看出,截止吸收能量稍高于或等于上文计算的禁带宽度,由于光子-电子的耦合能够引起占据态和非占据态之间的跃迁,因此截止吸收能量应大于或至少等于材料的禁带宽度[32].

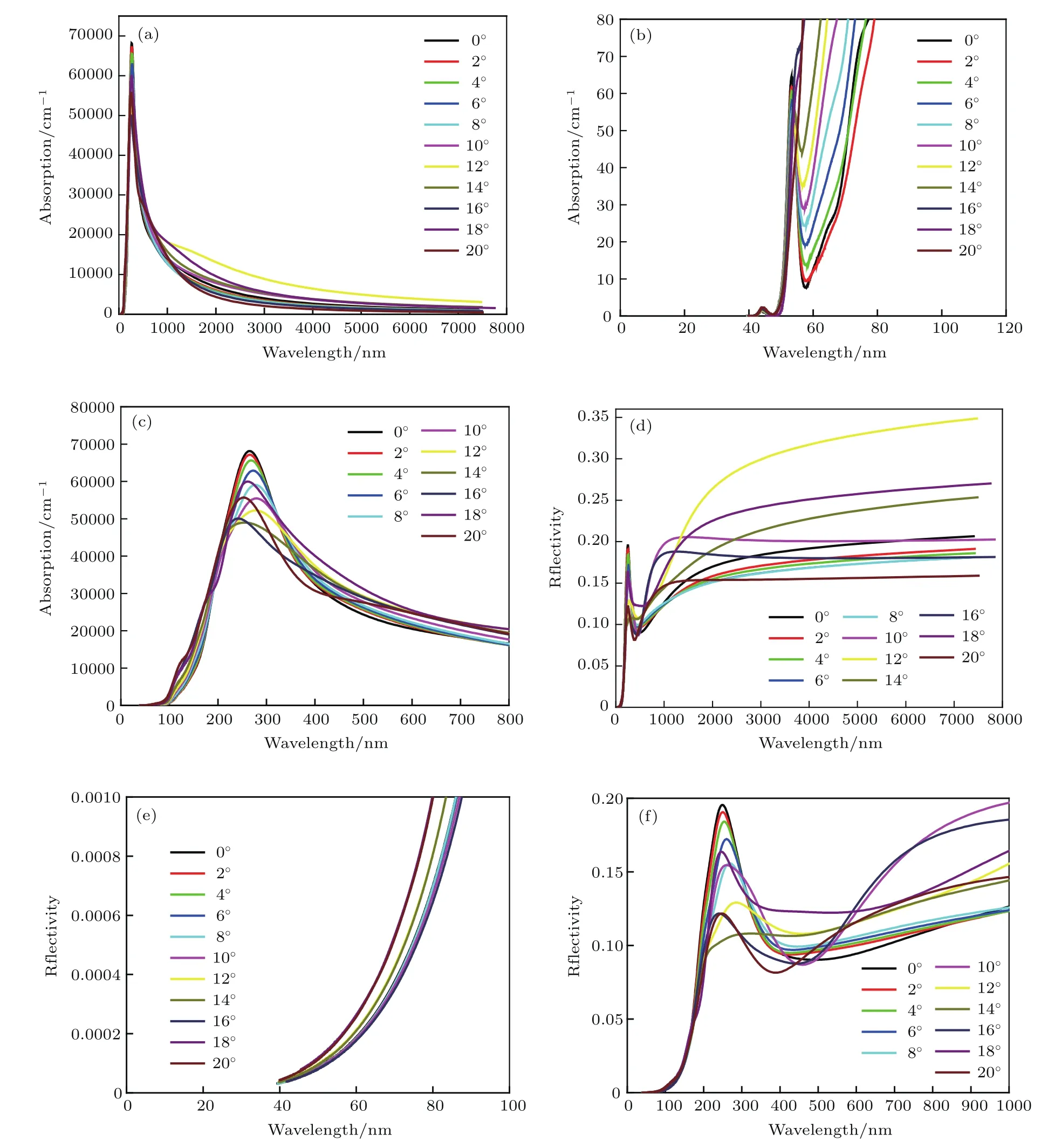
图7 (网刊彩色)石墨烯吸附O原子体系在转角0°,2°,4°,6°,8°,10°,12°,14°,16°,18°,20° 下的(a)光吸收系数和(d)反射率;(b),(c)为(a)在不同波长处的局部放大图;(e),(f)为(d)在不同波长处的局部放大图Fig.7.(color online)(a)Light absorption coefficent and(d)re fl ectivity of O atom absorbed on graphene with 0°,2°,4°,6°,8°,10°,12°,14°,16°,18°,20° torsion angle;(b),(c)the enlarged view of(a)at the different wavelength;(e),(f)the enlarged view of(d)at different wavelength.

从图7(d)可以看出,所有反射峰出现在波长约为260 nm处,波长超过1350 nm时,扭转角为12°的吸附体系对光的反射作用最强.扭转角为10°,16°,18°的吸附体系在波长为7860 nm处停止对光的反射,其余体系在波长为7434 nm处停止对光的反射.从图7(e)可以看出,所有吸附体系在波长为40 nm处开始对光进行反射,扭转角为18°和20°的吸附体系的光反射率重合并且增长得最快;扭转角为6°的吸附体系的反射率增长最慢.从图7(f)可以看出,在反射峰处,扭转吸附体系较未受扭转体系的反射率降低,反射峰值按照扭转角0°,2°,4°,6°,18°,8°,10°,12°,16°,14°的顺序依次降低(20°体系与16°体系峰值相同).扭转形变使扭转角为2°—14°的体系峰值发生红移,并使扭转角为16°—20°的体系峰值发生蓝移.

表3 石墨烯吸附O原子在不同扭转角下的带隙值和截止吸收能量Table 3.The band gaps and energy of cut-off absorption of O atom adsorbed on graphene with different torsion angle.

4 结 论

利用第一性原理研究了扭转形变对石墨烯吸附O原子体系结构稳定性、电子结构和光学性质,包括吸附能、带隙、吸收系数及反射率.结果表明,吸附O原子后,距O原子最近的C原子被拔起,导致石墨烯平面发生扭曲;扭转形变使石墨烯吸附O原子体系的结构稳定性下降,而扭转程度对结构稳定性的影响微弱;O原子的吸附使石墨烯由金属变成半导体,扭转形变发生时,可实现其从半导体到金属、再到半导体特性的转变;扭转角为12°的吸附O原子体系为间接带隙,而其他出现带隙的体系均为直接带隙;与本征石墨烯受扭体系相比,吸附O原子体系的电子结构对扭转形变的敏感度降低,其中扭转角在10°—16°范围内变化时,带隙始终稳定在0.11 eV附近,即在此扭转角范围内始终对应窄带隙半导体;受扭转形变的吸附体系吸收系数和反射率峰值较未受扭转形变石墨烯吸附O原子的体系均减弱,且随着扭转程度的加剧,均出现红移到蓝移的转变.

[1]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004Science306 666

[2]Castro A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009Rev.Mod.Phys.81 109

[3]Novoselov K,Fal V,Colombo L,Gellert P,Schwab M,Kim K 2012Nature490 192

[4]Mayorov A S,Gorbachev R V,Morozov S V,Britnell L,Jalil R,Ponomarenko L A,Blake P,Novoselov K,Watanabe K,Taniguchi T,Geim A K 2011Nano Lett.11 2396

[5]Novoselov K S,Geim A K,Morozov S V,Jiang D,Katsnelson M I,Grigorieva I V,Dubons S V,Firsov A A 2005Nature438 197

[6]Gong K P,Du F,Xia Z H,Durstock M,Dai L M 2009Science323 760

[7]Yang L J,Jiang S J,Zhao Y,Zhu L,Chen S,Wang X Z,Wu Q,Ma J,Ma Y W,Hu Z 2011Angew.Chem.Int.Ed.50 7132

[8]Sun J P,Zhou K L,Liang X D 2015Acta Phys.Sin.64 018201(in Chinese)[孙建平,周科良,良晓东2015物理学报64 018201]

[9]Prasai D,Tuberquia J C,Harl R R,Jennings G K,Bolotin K I 2012ACS Nano6 1102

[10]Pu N,Shi G,Liu Y,Sun X,Chang J,Sun C,Cer M,Chen C,Wang P,Peng Y,Wu C,Lawes S 2015J.Power Sources282 248

[11]Zhou S,Liu G L,Fan D Z 2017Physica B506 156

[12]Shenoy V B,Reddy C D,Ramasubramaniam A,Zhang Y W 2008Phys.Rev.Lett.101 245501

[13]Han M Y,Ouml,Zyilmaz B,Zhang Y,Kim P 2007Phys.Rev.Lett.98 206805

[14]Singh A K,Penev E S,Yakobson B I 2010ACS Nano4 2510

[15]Li J,Zhang Z H,Wang C Z,Deng X Q,Fan Z Q 2012Acta Phys.Sin.61 056103(in Chinese)[李骏,张振华,王成志,邓小清,范志强2012物理学报61 056103]

[16]Segall M D,Lindan P J D,Probert M J,Pickard C J,Hasnip P J,Clark S J,Payne M C 2002J.Phys.:Condens.Matter14 2717

[17]Perdew J P,Burke K 1996Phys.Rev.Lett.77 3865

[18]Vanderbilt D 1990Phys.Rev.B41 7892

[19]Monkhorst H J,Pack J D 1976Phys.Rev.B13 5188

[20]Shanno D F 1970Math.Comp.24 647

[21]Carlsson J M,Scheラer M 2006Phys.Rev.Lett.96 046806

[22]Jin F,Zhang Z Y,Wang C Z,Deng X Q,Fan Z Q 2012Acta Phys.Sin.61 036103(in Chinese)[金峰,张振华,王成志,邓小清,范志强2012物理学报61 036103]

[23]Avouris P,Chen Z,Perebeinos V 2007Nat.Nanotech.2 605

[24]Sun J P,Miu Y M,Cao X C 2013Acta Phys.Sin.62 036301(in Chinese)[孙建平,缪应蒙,曹相春2013物理学报62 036301]

[25]Yu Z,Dang Z,Ke X Z,Cui Z 2016Acta Phys.Sin.65 248103(in Chinese)[禹忠,党忠,柯熙政,崔真 2016物理学报65 248103]

[26]Varyhalov A,Sanchez B J,Shikin A M,Biswas C,Vescovo E,Rybkin A,Marchenko D,Rader O 2008Phys.Rev.Lett.101 157601

[27]Bao C,Yao W,Wang E,Chen C,Avila J,Asensio M C,Zhou S Y 2017Nano Let.17 1564

[28]Horiuchi S,Gotou T,Fujiwara M,Sotoaka R,Hirata M,Kimoto K,Asaka T,Yokosawa T,Matsui Y,Watanabe K,Sekita M 2003Jpn.J.Appl.Phys.42 L1073

[29]Balog R,Jørgensen B,Nilsson L,Andersen M,Rienks E,Bianchi M,Fanetti M,Laegsgaard E,Baraldi A,Lizzit S,Sljivancanin Z,Besenbacher F,Hammer B,Pedersen T G,Hofmann P,Hornekaer L 2010Nat.Mater.9 315

[30]Eroms J,Weiss D 2009New J.Phys.11 095021

[31]Kim M,Safron N S,Han E,Arnold M S,Gopalan P 2010Nano Lett.10 1125

[32]Hu Z G,Duan M Y,Xu M,Zhou X,Chen Q Y,Dong C J,Linghu R F 2009Acta Phys.Sin.58 1166(in Chinese)[胡志刚,段满益,徐明,周勋,陈青云,董成军,令狐荣锋2009物理学报58 1166]