混沌光注入垂直腔面发射激光器混沌输出的时延和带宽特性∗

苏斌斌 陈建军2) 吴正茂 夏光琼

1)(西南大学物理科学与技术学院,重庆 400715)2)(新疆医科大学医学工程技术学院,乌鲁木齐 830011)

(2017年6月30日收到;2017年7月21日收到修改稿)

1 引 言

半个世纪以来,混沌因其在基础科学和应用科学领域所展现出巨大的应用前景而受到极大关注.作为混沌领域的一个重要分支,激光混沌已广泛应用于混沌保密通信、混沌雷达、高速随机数产生等领域[1−9].已有研究表明:半导体激光器(SLs)在光反馈[10,11]、光注入[12−14]和光电反馈[15,16]等外部扰动作用下均可获得混沌光输出,其中光反馈SLs混沌系统由于结构简单、易于控制、可产生复杂混沌光而被认为是理想的混沌源之一.

近年来,随着社会信息化程度的不断提高,人们对信息传输有着越来越高的要求,而兼有高保密性、大传输速率的混沌保密通信正日益受到人们的关注.在混沌保密通信中,信息传输过程中的安全性依赖于进行高维混沌吸引子重构时的计算复杂程度[17].相比较其他外部扰动而言,光反馈SLs系统更易产生高维激光混沌.然而,由于光在外腔中来回反射,使系统输出的混沌信号具有明显的延时特征(TDS)[18],这可能导致高维混沌在相空间内的投影成为低维混沌,窃听者可根据此特性将混沌信号重构,从而严重威胁通信安全[19].因此,如何获取TDS得到抑制的混沌载波是混沌保密通信所需解决的关键问题之一[20−23].已有的研究表明,单光反馈SLs输出混沌信号TDS仅在反馈延迟时间与弛豫振荡近似相等时可以得到一定程度的抑制[20].而双光反馈SLs系统由于引入了新的自由度,因而有着更为复杂的混沌信号输出.相关研究结果已证实,在合适的反馈参数条件下,双光反馈SLs输出混沌信号的TDS可得到更为有效的抑制[21].上述研究大多是基于边发射分布反馈半导体激光器(DFB-SLs)所开展的.

相比于边发射SLs,垂直腔面发射激光器(VCSELs)具有单纵模输出、阈值电流低、调制速率高、与光纤耦合损耗小、易于集成激光阵列等独特优点[24−26].特别地,VCSELs腔体结构的圆对称性和腔内增益介质的弱各向异性导致其有可能同时输出两个正交的偏振分量(X-PC和Y-PC),将其分别用作两路混沌载波有利于提高混沌保密通信系统的通信容量.最近,Lin等[27]的实验研究证实VCSEL在双外腔反馈(DOF)作用下,两个正交偏振分量输出的混沌信号的TDS均可达到较好的抑制.然而,由于受限于VCSELs的弛豫振荡的限制,所获得的混沌带宽较小(几个GHz水平),使其在高速混沌保密通信中的应用有一定局限性.

本课题组在前期的研究工作中发现:通过将一个单光反馈作用下的VCSEL(定义为主VCSEL,M-VCSEL)所产生的混沌信号注入到另外一个VCSEL(定义为副VCSEL,S-VCSEL),在合适的注入参数条件下S-VCSEL输出混沌信号比MVCSEL输出的混沌信号具有更弱的TDS、更宽的混沌带宽[28].在此基础上,考虑到DOF比单外腔反馈(SOF)更利于获取弱TDS混沌信号[27]以及通过混沌光注入可进一步对混沌信号性能提升[28],本文提出并仿真论证了由一个双光反馈作用下的M-VCSEL和另一个VCSEL(S-VCSEL)构成的主副混沌系统,通过将M-VCSEL产生的混沌光注入到S-VCSEL中,以同时实现混沌信号TDS的进一步抑制以及带宽的增强,从而达到获取两路高质量的混沌信号的目的.

2 系统与理论模型

图1为主副VCSELs混沌系统的结构示意图.M-VCSEL输出的光信号经准直透镜(AL)后被分束器(BS1)分成两部分.其中一部分光经中性密度衰减片(NDF1)、平面镜(M1)反馈回M-VCSEL;另一部分则经另外一个分束器(BS2)再次分成两部分,其中一部分经过NDF2和M2后反馈回M-VCSEL中,而另外一部分经光隔离器(ISO)和NDF3后注入进S-VCSEL.其中,ISO用于确保光单向传输;NDF1,NDF2分别用于调节M-VCSEL两个反馈腔的反馈强度,而NDF3则用于调节光注入进S-VCSEL的强度.通过调节M1或M2的位置,可改变反馈腔1和反馈腔2的反馈延迟时间.

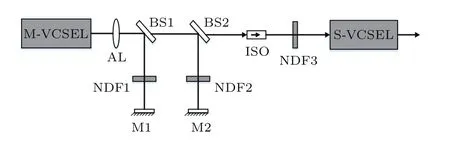
图1 主副VCSELs混沌系统的结构图(M-VCSEL,主VCSEL;S-VCSEL,副VCSEL;AL,透镜;BS,分束器;M,平面镜;NDF,中性密度衰减片;ISO,光隔离器)Fig.1.Schematic diagram of a master-slave VCSELs chaotic system.M-VCSEL,master VCSEL;SVCSEL,slave VCSEL;AL,aspheric lens;BS,beam splitter;M,mirror;NDF,neutral density fi lter;ISO,optical isolator.

基于自旋反转模型[29,30],双光反馈作用下的M-VCSEL以及光注入下的S-VCSEL的速率方程组可描述为[31,32]

式中,上标m和s分别表示M-VCSEL和S-VCSEL;下标1,2分别表征反馈腔1和反馈腔2;下标X,Y分别表示VCSELs的X偏振分量(X-PC)和Y偏振分量(Y-PC),X-PC和Y-PC分别沿着VCSEL有源区两个正交的晶轴方向.E表示光场的慢变复振幅,N表示VCSELs导带与价带之间总的反转载流子密度,n表示自旋向上与自旋向下能级对应的载流子密度之差,k表示光场衰减率,α表示线宽增强因子,γe为总载流子的衰减速率,γs为自旋反转速率,µ为归一化偏置电流.考虑到VCSEL有源区生长过程中弹光效应和电光效应导致激光器的圆形横向对称性被破坏从而导致线性极化呈现各向异性,其中幅度的各向异性(即二向色性)用γa描述,而相位的各向异性(即双折射)用γp表征,双折射将导致X-PC和Y-PC的激射频率存在差异[33].f表征反馈强度,η表征从M-VCSEL注入到S-VCSEL的注入强度,τ1和τ2为M-VCSEL两个反馈腔的反馈延迟时间,τc为MVCSEL输出的混沌光注入到S-VCSEL的反馈延迟时间,νm与νs分别为M-VCSEL和S-VCSEL的中心频率,Δν=νm−νs为频率失谐.F为朗之万噪声源[25],表示为

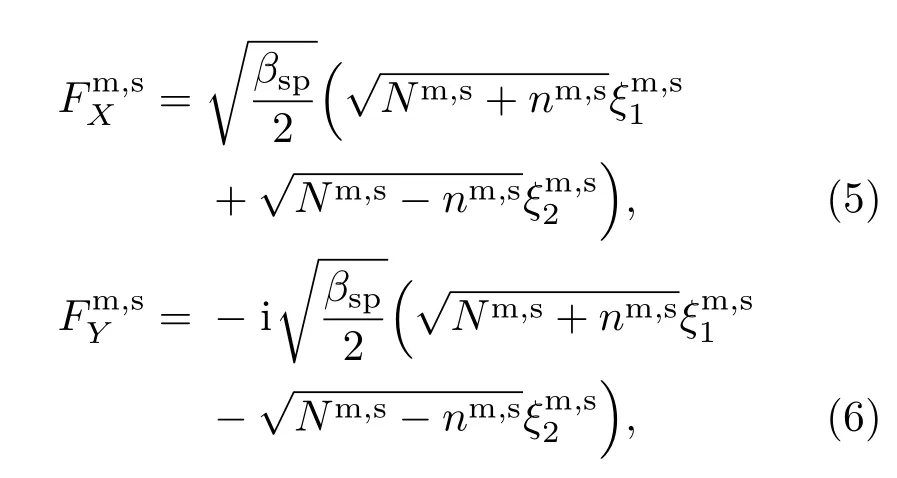
其中,ξ为高斯白噪音,其平均值为0,方差为1;βsp为自发辐射速率.

本文采用自相关(SF)[31]分析方法对时滞系统的TDS进行评估.其中,SF定义为[34]

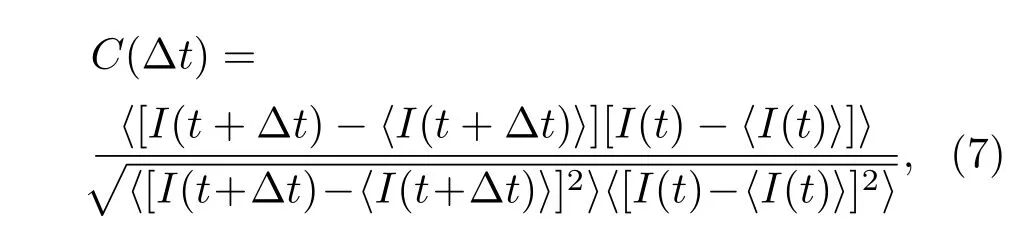
式中,Δt表示时移,I(t)表征VCSEL混沌输出时间序列,〈·〉表示时间平均值.σ为SF函数C(Δt)在时移Δt位于反馈延迟时间附近的最大峰值,σ值越大,混沌系统的TDS越明显.计算SF时所采用的混沌时间序列长度为2000 ns,步长2 ps.

另外,采用有效带宽(EBW)[35,36]来标定混沌信号的带宽.EBW的计算方法为:将整个频谱中的能量成分依次从高到低排序,然后累加至整个谱中能量成分的80%,此时包含的频率范围即为混沌信号的EBW.

3 结果与讨论

利用四阶Runge-Kutta算法可对速率方程组(1)—(4)进行数值仿真.在数值仿真过程中,假定两个VCSELs具有相同的内部参数,所采用的内部参数如下[37]:k=300 ns−1,a=3,γs=50 ns−1,γp=10 ns−1,γe=1 ns−1,γa=0.1 ns−1,τc=0 ns,βsp=10−6ns−1,S-VCSEL的中心频率νs=3.529×1014GHz(对应的中心波长为850 nm).

图2给出了自由运行下VCSEL两个正交的偏振分量及总的输出平均功率随归一化电流的P-µ曲线.在数值分析中,归一化电流µ的取值范围为0—3.5.由图2可知:当µ大于1时,X-PC处于激射状态,Y-PC被抑制;当µ增加到1.7时,Y-PC也开始起振,随着µ的进一步增加,Y-PC的功率迅速增加而X-PC的功率增长趋势缓慢;当µ增加至2.7时,此时自由运行VCSEL输出的两个分量具有相同的功率;之后,随着µ的增加,Y-PC的输出功率将大于X-PC的输出功率,系统输出以Y-PC为主导.鉴于µ=2.7时激光器的两偏振分量具有相同的输出平均功率,有利于获取两路混沌信号.因此在下面的讨论中,取µ=2.7,此时激光器的弛豫振荡频率为5.08 GHz,弛豫振荡周期τR≈0.19 ns.

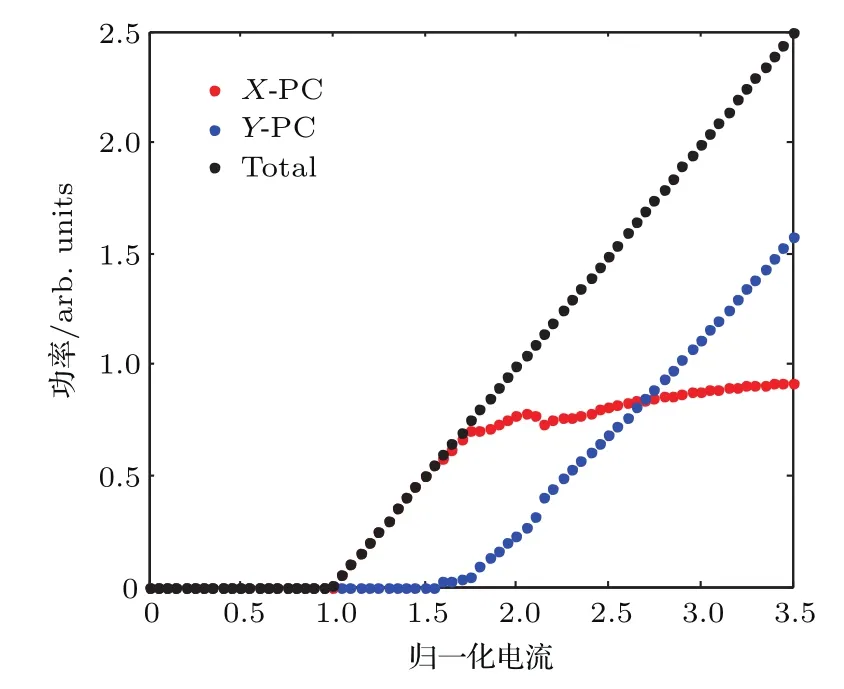
图2 (网刊彩色)自由运行VCSEL偏振分量的P-µ曲线Fig.2.(color online)Polarization-resolved P-µcurves of free-running VCSEL.

3.1 M-VCSEL输出混沌信号的TDS

已有的研究表明,双外腔系统混沌信号的TDS强烈依赖于两个腔的反馈参量[21].这里假定两个腔具有相同的反馈强度,腔1的反馈时间τ1=3 ns[31],讨论反馈腔2的反馈延迟时间对M-VCSEL输出混沌TDS的影响.图3给出了当f1=f2=10 ns−1时,M-VCSEL输出的(a)X-PC和(b)Y-PC时间序列的SF函数峰值σ随τ2的变化曲线.如图3所示,两个偏振分量输出混沌信号的SF峰值σ随τ2变化均呈现波动,且两个偏振分量输出的混沌信号的SF峰值σ取极小值时所需的τ2的值存在差异.结合图3(a)和图3(b)可以看出,当τ2=3.09 ns时,Y-PC输出的混沌信号的σ值非常低,而同时X-PC输出的混沌信号的σ值也相对较小.因此,在接下来的讨论中,τ2的值设定为3.09 ns.

在双光反馈系统中,若两个外腔的反馈参数完全一致,则DOF过渡为SOF.图4给出了(a)SOF及(b)DOF条件下M-VCSEL两个偏振分量输出混沌的时间序列及其对应的SF曲线.从图中可以看出,尽管SOF作用时M-VCSEL两个偏振分量输出的时间序列依然为混沌,但其对应的X-PC和Y-PC的SF曲线在反馈延迟时间附近出现了明显的峰值,分别为0.54和0.57.说明此时系统输出的混沌信号具有明显的TDS;而对于DOF的情形,X-PC和Y-PC输出混沌信号的SF峰值相较于SOF情形显著减小,分别为0.20和0.16,说明此时混沌输出信号具有弱的TDS.

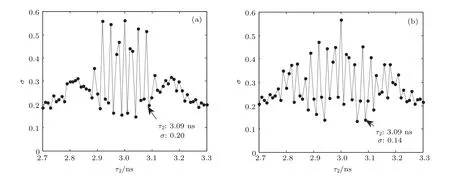
图3 M-VCSEL的(a)X-PC与(b)Y-PC时间序列SF峰值σ随τ2的变化Fig.3.Dependence of characteristic peak of SF of time series on τ2for(a)X-PC and(b)Y-PC of M-VCSEL.

图4 (a)SOF和(b)DOF条件下M-VCSEL的X-PC和Y-PC输出混沌的时间序列及其对应的SF曲线Fig.4.Time series and SF curves of X-PC and Y-PC chaotic outputs of M-VCSEL under(a)SOF and(b)DOF.

3.2 混沌光注入下S-VCSEL输出混沌信号的TDS

上述研究结果表明,通过优化DOF的反馈参量,可使M-VCSEL两偏振分量输出混沌的TDS得到一定程度的抑制.接下来研究在优化条件下M-VCSEL输出的混沌信号平行注入到另外一个VCSEL(副VCSEL,S-VCSEL)中所获得的两路正交混沌信号的TDS随注入参数的演化规律.图5给出了频率失谐Δν取−10,0以及10 GHz时,S-VCSEL两个正交的偏振分量输出混沌信号的TDS峰值σ随注入强度η的变化曲线.需要指出的是,由于仅当η＞4 ns−1时,S-VCSEL的两个偏振分量才呈现混沌输出,因此只对η＞4 ns−1的情形进行分析.如图5所示,对于所给的频率失谐下,当4 ns−1＜η＜100 ns−1时X-PC和Y-PC输出的混沌信号的σ值均小于由M-VCSEL输出的对应偏振分量的σ值,即在该范围内,两个偏振分量的输出混沌的TDS均可得到进一步抑制.特别地,当4 ns−1＜η＜40 ns−1时,S-VCSEL两偏振分量输出混沌信号的σ值均在0.1以下,表明混沌输出信号的TDS得到了有效抑制.

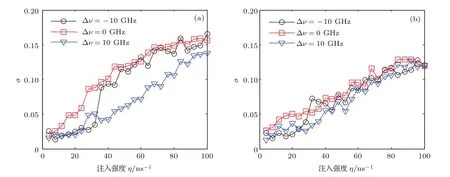
图5 (网刊彩色)Δν=−10,0,10 GHz时,S-VCSEL的(a)X-PC和(b)Y-PC输出混沌TDS峰值σ随注入强度η的变化Fig.5.(color online)Relationship between the peak σ and injection strength η for TDS of(a)X-PC and(b)Y-PC chaotic outputs from S-VCSEL under detuning frequency Δν= −10,0,10 GHz,respectively.

图6 (网刊彩色)S-VCSEL的 (a)X-PC和 (b)Y-PC的TDS σ值随η和Δν的演化图Fig.6.(color online)Evolution map of σ for TDS of(a)X-PC and(b)Y-PC of the S-VCSEL in the parameter space of η and Δν.

为进一步更清晰地呈现频率失谐Δν和注入强度η对S-VCSEL输出混沌信号TDS的影响,图6给出了S-VCSEL两个偏振分量输出混沌的SF函数的σ值在由频率失谐Δν和注入强度η构成的参数空间演化图.图中无色区域表征S-VCSEL两偏振分量输出的信号并非混沌信号,有色区域则对应S-VCSEL在混沌光注入的驱动下呈现混沌态,不同的颜色表征不同的σ值.黑色虚线表示σ值为0.1,在黑色虚线围成的深蓝色区域则对应σ值小于0.1.从图6可以看出,S-VCSEL两个偏振分量输出混沌信号的TDS被有效抑制的参数区域均呈现出“V”字形分布特征,但Y-PC输出混沌信号的σ＜0.1所需的参数区域更大.其原因是注入的混沌信号中,X-PC的TDS相对较大所导致的.

3.3 M-VCSEL和S-VCSEL输出混沌信号的EBW特性

接下来讨论将M-VCSEL输出的混沌光注入到S-VCSEL后所产生的混沌信号带宽随注入参量的变化.图7给出了当注入强度η=50 ns−1,Δν=−20 GHz时,S-VCSEL在M-VCSEL产生的混沌光注入下X-PC与Y-PC输出的时间序列与功率谱.为了比较,由M-VCSEL所产生的注入光的时间序列以及功率谱也在图7中给出.图中功率谱的阴影区域为EBW的提取区域.从图7可以看出,由双光反馈M-VCSEL所提供的注入XPC和Y-PC混沌信号的EBW分别为10.72 GHz和10.10 GHz,其平行注入到S-VCSEL后,所获得的X-PC和Y-PC混沌输出的功率谱更加平坦,EBW分别达到20.13 GHz与18.63 GHz.这是由于光注入到S-VCSEL中,注入光与S-VCSEL激射光的拍频效应将在拍频频率处提供一个增益,导致在拍频频率(20 GHz)附近的功率分布得到加强,从而导致S-VCSEL输出混沌的带宽得到展宽.

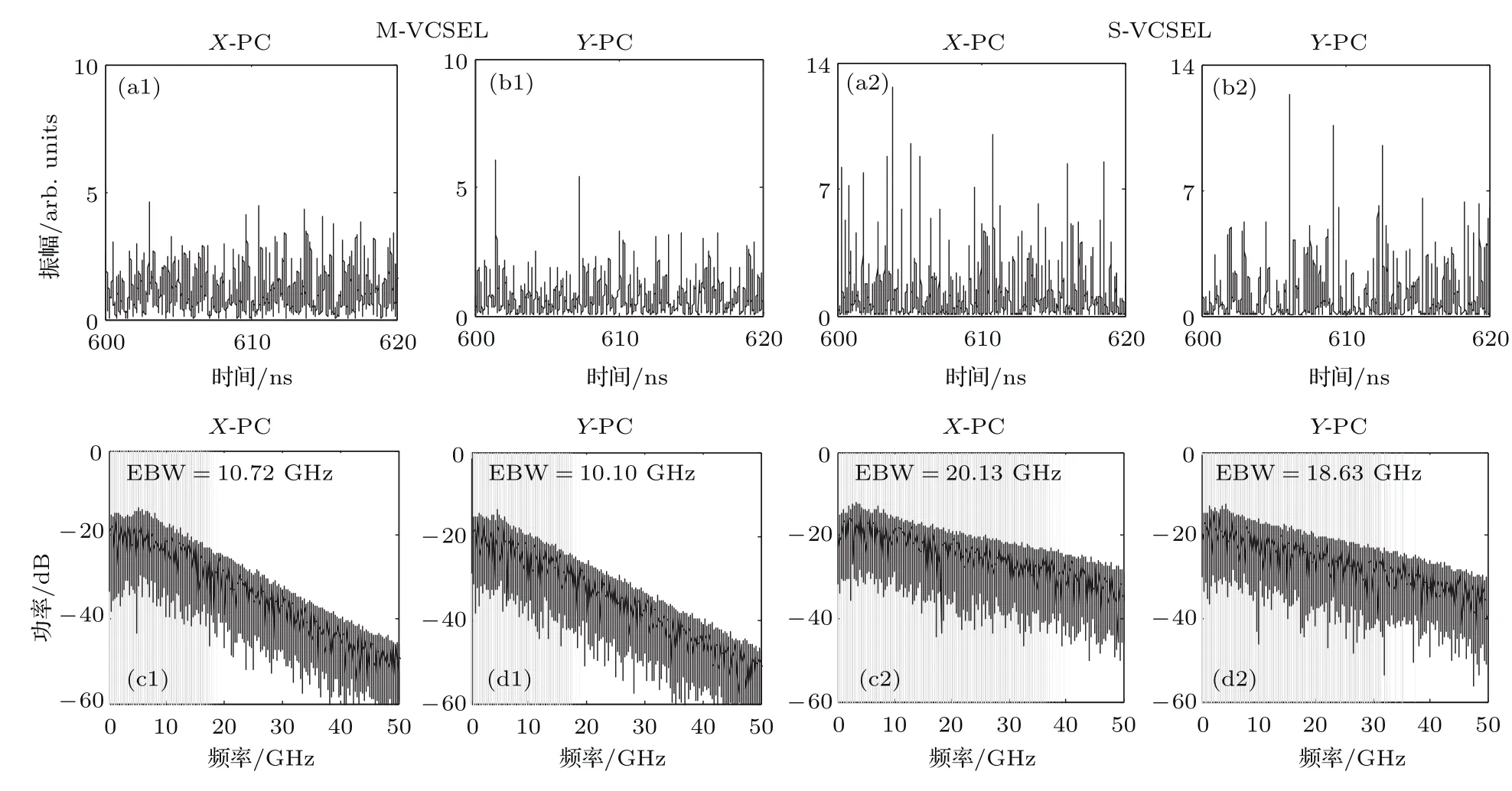
图7 M-VCSEL的X-PC与Y-PC混沌输出的(a1),(b1)时间序列与(c1),(d1)功率谱及当η=50 ns−1,Δν= −20 GHz时,S-VCSEL的X-PC与Y-PC在M-VCSEL产生混沌光注入下其混沌输出的(a2),(b2)时间序列与(c2),(d2)功率谱Fig.7.Chaotic outputs(a1),(b1)time series and(c1),(d1)power spectra of X-PC and Y-PC of M-VCSEL;chaotic outputs(a2),(b2)time series and(c2),(d2)power spectra of X-PC and Y-PC of S-VCSEL with η =50 ns−1and Δν = −20 GHz.

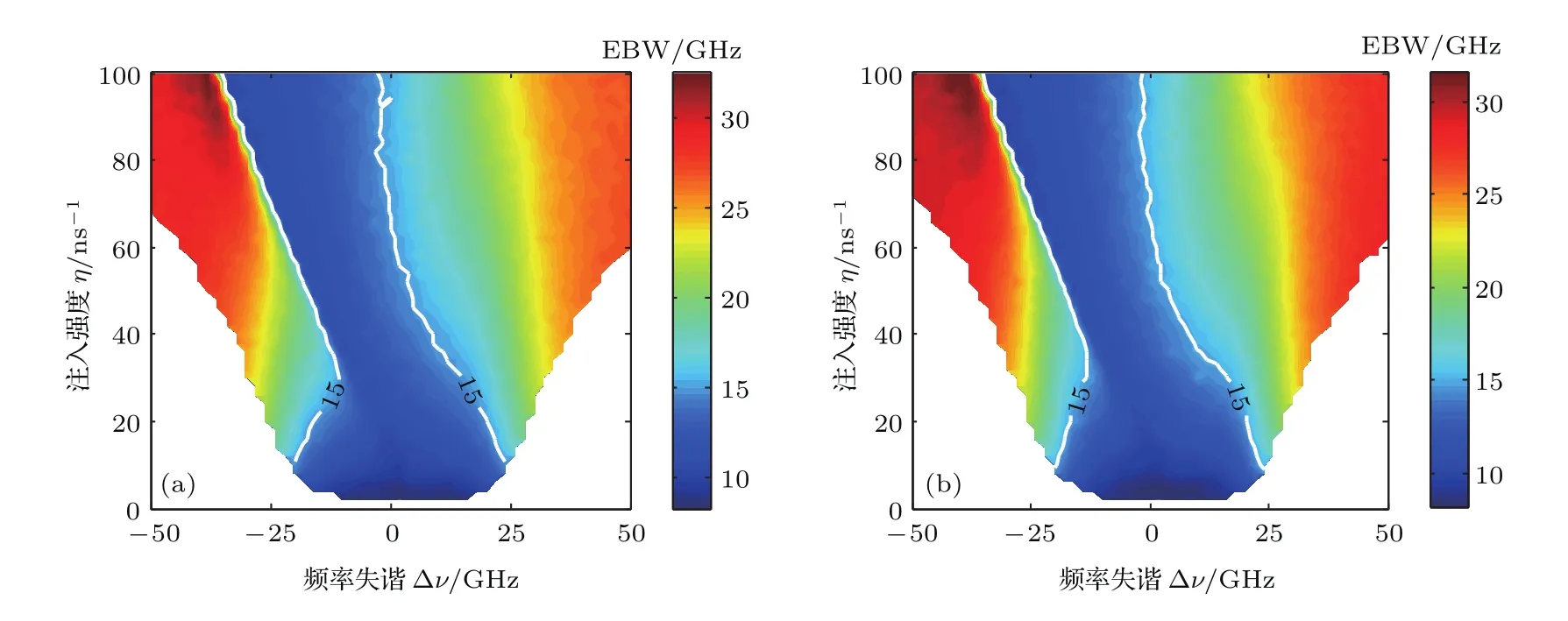
图8 (网刊彩色)S-VCSEL的(a)X-PC和(b)Y-PC的EBW随Δν和η的演化图Fig.8.(color online)Mappings of EBW evolution of(a)X-PC and(b)Y-PC of the S-VCSEL in the parameter space of Δν and η.

为了系统分析M-VCSEL产生的混沌光注入到S-VCSEL后最终获取的混沌信号带宽与注入参量的关联关系,图8给出了S-VCSEL的两偏振分量输出混沌的带宽在由η和Δν所构成参数空间内的分布图.图中不同的颜色对应于不同的混沌带宽,白色虚线表示带宽为15 GHz的参数位置.这些虚线将参数空间各自分成三个区域,中间的深蓝色区域表示带宽低于15 GHz.在这一区域中频率失谐相对较小,S-VCSEL主要呈现非稳定的注入锁定,即其动力学行为跟随M-VCSEL的动力学行为,因此导致其混沌带宽与M-VCSEL输出的混沌信号带宽相比拟.而对于频率失谐更大以及注入强度更强的区域,X-PC和Y-PC输出混沌的带宽均得到明显增强.通过结合图6的结果,可得到获取两路弱TDS、宽带宽的混沌信号所需的注入参数范围.

4 结 论

基于VCSEL自旋反转模型并结合对时间序列的SF分析方法,数值研究了由一个双光反馈MVCSEL与另一个S-VCSEL构成的主副混沌系统所产生的混沌信号的TDS和EBW特性.研究结果表明:通过选取合适的双光反馈系统参量,MVCSEL的两个偏振分量可输出TDS相对较弱的混沌信号;将该信号注入到S-VCSEL中,通过优化注入强度以及频率失谐,可得到TDS进一步弱化、带宽得到显著增强的两路混沌信号;结合S-VCSEL两偏振分量混沌输出的TDS以及带宽在由注入强度以及频率失谐构成的参数空间的演化图,可确定系统同时输出两路具有低TDS、宽带宽的混沌信号所需的参数范围.

[1]Argyris A,Syvridis D,Larger L,Annovazzi-Lodi V,Colet P,Fischer I,García-Ojalvo J,Mirasso C R,Pesquera L,Shore K A 2005Nature438 343

[2]Li N Q,Pan W,Luo B,Yan L S,Zou X H,Jiang N,Xiang S Y 2012IEEE Photon.Technol.Lett.24 1072

[3]Liu J,Wu Z M,Xia G Q 2009Opt.Express17 12619

[4]Zhong D Z,Deng T,Zheng G L 2014Acta Phys.Sin.63 70504(in Chinese)[钟东洲,邓涛,郑国梁2014物理学报63 70504]

[5]Lin F Y,Liu J M 2004IEEE J.Sel.Top.Quantum Electron.10 991

[6]Oliver N,Soriano M C,Sukow D W,Fischer I 2013IEEE J.Quantum Electron.49 910

[7]Uchida A,Amano K,Inoue M,Hirano K,Naito S,Someya H,Oowada I,Kurashige T,Shiki M,Yoshimori S,Yoshimura K,Dovis P 2008Nat.Photon.2 728

[8]Sakuraba R,Iwakawa K,Kanno K,Uchida A 2015Opt.Express23 1470

[9]Wang A B,Li P,Zhang J G,Zhang J Z,Li L,Wang Y C 2013Opt.Express21 20452

[10]Rontani D,Locquet A,Sciamanna M,Citrin D S,Ortin S 2009IEEE J.Quantum Electron.45 879

[11]Kong L Q,Wang A B,Wang H H,Wang Y C 2008Acta Phys.Sin.57 2266(in Chinese)[孔令琴,王安邦,王海红,王云才2008物理学报57 2266]

[12]Zhang L Y,Pan W,Yan L S,Luo B,Zou X H,Xiang S Y,Li N Q 2012IEEE Photon.Technol.Lett.24 1693

[13]Hwang S K,Liu J M 2000Opt.Commun.183 195

[14]Yan S L 2012Acta Phys.Sin.61 160505(in Chinese)[颜森林 2012物理学报61 160505]

[15]Lin F Y,Liu J M 2003IEEE J.Quantum Electron.39 562

[16]Zhang W L,Pan W,Luo B,Li X F,Zou X H,Wang M Y 2007Appl.Opt.46 7262

[17]Bandt C,Pompe B 2002Phys.Rev.Lett.88 174102

[18]Guo Y Y,Wu Y,Wang Y C 2012Chin.Opt.Lett.10 061901

[19]Short K M,Parker A T 1998Phys.Rev.E58 1159

[20]Rontani D,Locquet A,Sciamanna M,Citrin D S 2007Opt.Lett.32 2960

[21]Wu J G,Xia G Q,Wu Z M 2009Opt.Express17 20124

[22]Zhu X H,Cheng M F,Deng L,Jiang X X,Ke C J,Zhang M M,Fu S N,Tang M,Shum P,Liu D M 2017IEEE Photon.J.9 6601009

[23]Ke J X,Yi L L,Hou T T,Hu Y,Xia G Q,Hu W S 2017IEEE Photon.J.9 7200808

[24]Iga K 2000IEEE J.Sel.Top.Quantum Electron.6 1201

[25]Xiang S Y,Pan W,Luo B,Yan L S,Zou X H,Jiang N,Li N Q,Zhu H N 2012IEEE Photon.Technol.Lett.24 1267

[26]Zhang X X,Zhang S H,Wu T A,Sun W Y 2016Acta Phys.Sin.65 214206(in Chinese)[张晓旭,张胜海,吴天安,孙巍阳2016物理学报65 214206]

[27]Lin H,Hong Y H,Shore K A 2014J.Lightwave Technol.32 1829

[28]Yang X J,Chen J J,Xia G Q,Wu J G,Wu Z M 2015Acta Phys.Sin.64 224213(in Chinese)[杨显杰,陈建军,夏光琼,吴加贵,吴正茂2015物理学报64 224213]

[29]San Miguel M,Feng Q,Moloney J V 1995Phys.Rev.A52 1728

[30]Martin-Regalado J,Prati F,San Miguel M,Abraham N B 1997IEEE J.Quantum Electron.33 765

[31]Xiao P,Wu Z M,Wu J G,Jiang L,Deng T,Tang X,Fan L,Xia G Q 2013Opt.Commun.286 339

[32]Liu H J,Li N Q,Zhao Q C 2015Appl.Opt.54 4380

[33]Sodermann M,Weinkath M,Ackemann T 2004IEEE J.Quantum Electron.40 97

[34]Elsonbaty A,Hegazy S F,Obayya S S A 2015IEEE J.Quantum Electron.51 2400309

[35]Lin F Y,Chao Y K,Wu T C 2012IEEE J.Quantum Electron.48 1010

[36]Kanno K,Uchida A,Bunsen M 2016Phys.Rev.E93 032206

[37]Zhong Z Q,Wu Z M,Wu J G,Xia G Q 2013IEEE Photon.J.5 1500409