一种改进的Philips音频指纹检索算法

,, ,

(1.上海音乐学院 a.音乐声学艺术重点实验室;b.音乐学系,上海 200031;2.上海计算机软件技术开发中心,上海 201112)

0 概述

音频指纹可以看作是音频信号的独一无二标识符,是通过音频特征提取算法,提取特定特征而形成的特征序列。因此,一段音频指纹,可以看成一段音频内容的概括,并且能够唯一表达这段音频信号。因为音频指纹能够唯一表达音频信号的特征,被广泛地应用于音频识别、音乐检索、内容识别、分类、版权内容监管等应用领域[1-3]。

音频指纹研究,核心内容包括2个部分:特征提取和检索算法。在音频特征提取的算法研究方面,目前国内外研究者已经提出大量算法,如文献[4-8]。其中,以荷兰Philips研究所[6]提出的基于相邻能力差的变化来提取指纹和英国Shazam公司[5]基于谱峰点对(Peak-Pairs)形成的特征对指纹序列为典型代表。

由于Philips指纹内容简单、容易实现、复杂度小、检索效率高等优点,被广泛应用。在Philips音频指纹检索系统中,结合指纹的特点,构造一个232查询表作为索引表,由于查询表太大,在应用中,利用哈希表代替查询表,并分别存放。本文针对Philips音频检索算法提出改进方法。结合斐波那契数列和右移运算,构造一个新的哈希函数,利用斐波那契数列优化哈希值分布,执行右移操作调整哈希表长度,优化内存使用,从而提升系统的实用性。

1 相关知识介绍

本文研究基于Philips系统模型,结合哈希表与斐波那契数列对Philips音频检索算法实施改进,本节先回顾相关知识。

1.1 Philips音频指纹的研究概况

Philips音频指纹研究包括指纹提取和音频检索。其音频指纹提取模型如图1所示。

图1 指纹提取模型

从图1可知,音频指纹提取包括4个步骤。

1)预处理。音频信号转化统一格式:单声道PCM(16 bit),44.1 KHz,MP3等操作。

2)分帧。即对音频信息进行分帧,这里是按照固定长度来进行。使用31/32重叠率,目的是抵消帧的边界误差,确保在最坏的情况下,真实指纹与查询指纹仍然相似。此外,对每一帧添加汉明窗。

3)提取频率子带。对每一帧执行傅里叶变换,将原始时域数字信号转化成频谱表示,选择与人类听觉最相关的频域:300 Hz～2 000 Hz频率带。接着,使用对数空间,将选择的频率带划分成33个非重叠的子带。

4)提取指纹。首先,基于相邻的频率子带的能量差符号推导字节,则第n帧的第m比特fn(m)定义为:

(1)

其中:

E=E(n,m)-E(n,m+1)-

E(n-1,m)+E(n-1,m+1)

(2)

基于式(1)字节推导,从33个非重叠的频率子带中提取32个连续比特形成一个指纹。

由于一个指纹信息量太少,在应用中,通常使用指纹块。设一个音频片段的指纹序列FP=f1f2…fN,块长为L,则第i指纹块定义为:

(3)

在Philips音频检索算法中,构造一个232的哈希表,检索模型如图2所示。

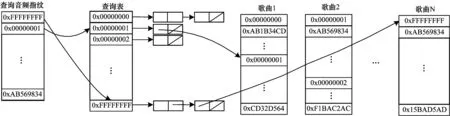
图2 指纹检索模型

在Philips检索模型中,将候选查询指纹作为查询表的关键字进行匹配,然后快速定位到真实的指纹文件,接着计算指纹块的相似度,根据阈值判断是否相似。

1.2 哈希表

哈希表是一种高效的数据结构,通过把关键字(key)映射到表中一个位置来访问记录,以加快查找的速度。其中,哈希函数即为映射函数,哈希表即是存放记录的数组。在大部分应用中,哈希表查找速度最快,其时间复杂度通常为常量,而且编程实现也相对容易。哈希表的原理其实就是通过空间换取时间的做法,哈希表示意图如图3所示。

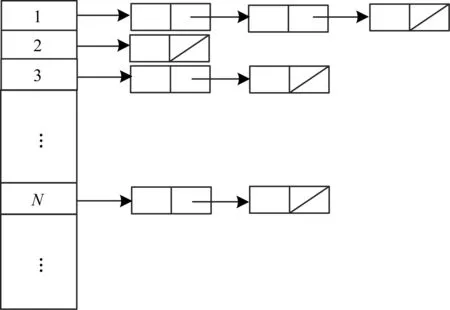
图3 哈希表结构示意图

在哈希表设计中,设计目标遵循2个原则[9]:

1)每一个key对应唯一一个哈希值。

2)哈希值能够均匀地分布到整个哈希表中。

但是,在实际的应用中,这种理想的设计很难实现,即哈希冲突不可避免[10]。

哈希冲突现象:2个关键字key1和key2,且key1≠key2,但他们的哈希值相等,即通过哈希函数映射到哈希表同一地址上的现象。

在实际应用中,哈希冲突的现象是避免不了的,但冲突的程度是能够通过一些手段和方法来减少的,例如改进哈希函数的性能。因此,解决哈希冲突的根本原则是设计一个好的哈希函数,减少冲突概率,即实现较好的哈希值分布。

1.3 斐波那契数列

在哈希表应用中,斐波那契散列发被广泛使用,其设计思想[11]:找出一个理想的乘数和key做乘法,目标实现哈希值的良好分布。

在文献[12]中,已经证明这个理想的数[13]与黄金分割法则[14]有关,其具体数字与黄金分割法则的经典表达斐波那契数列[15]吻合,其计算等式:

C≈Wλ-1

(4)

其中,W代表字长,λ-1代表黄金分割比例的倒数。根据式(4),容易计算不同字节的C值,结果如表1所示。

表1 斐波那契数列

在实验中,研究者们还发现,基于斐波那契数列的哈希分布有这样的现象:新添加的哈希值,落入按照黄金分割法则分割的最大空间中。

2 算法的改进

在Philips音频检索算法中,构造了一张232的查询表,由于内存消耗太大,在实际应用中,用哈希表代替查询表,并分别存储。此外,哈希表的利用率很低,一方面由于指纹数量远远小于哈希表的长度;另一方面,由于哈希值分布不均匀造成。例如,1万首歌曲大约对应2.5亿个指纹,据统计利用率不到0.058。

针对Philips指纹检索的上述缺陷,本文提出一个改进算法。首先,基于斐波那契数列和右移运算,构造一个新的哈希函数,基于这个哈希函数的映射,哈希值具有良好的分布;此外,根据实际的应用需求,执行右移操作控制哈希表的长度,具体实现将在下面子节中描述。

2.1 哈希函数的构造

针对Philips指纹检索的问题,首先设计一个哈希函数。

设计思想为利用斐波那契数列优化哈希值分布;接着,利用右移运算,结合具体的应用需求,灵活调整哈希表的长度,构造的哈希函数为:

f(FP)=(FP×C)>>N

(5)

其中,FP代表一个指纹,即相当一个32位的整数。C为斐波那契数列,从表1可以,C等于2654435769。N代表右移位数,范围1≤N≤32。N的取值主要取决于实际内存的大小。通过右移操作,得到的哈希值高N位全部变成0。

2.2 哈希表的构造

通过构造哈希函数,指纹的高N位变成0,基于这个事实,调整哈希表的长度:232-N,这样Philips哈希表模型改进如图4所示。

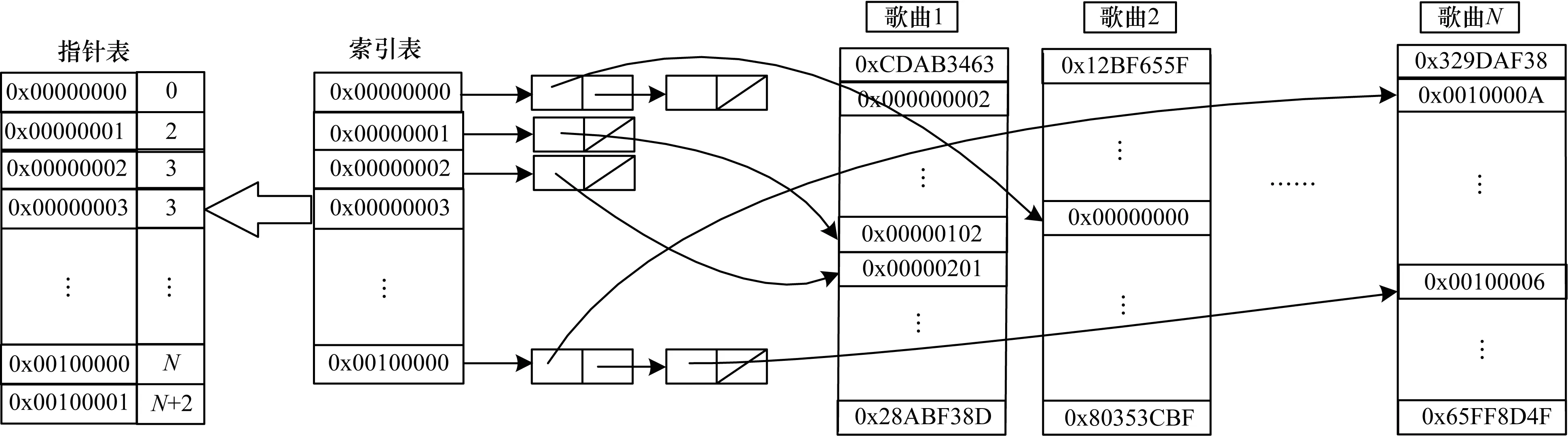
图4 哈希表模型

为了优化检索速度,提出如下的优化策略:

1)构造2个哈希表,一个叫做索引表,另一个叫做指针表。索引表存储真实指纹的地址信息;遍历索引表,从上到下,每一个关键字按照节点的先后顺序,进行编号,每一个关键字的最后一个节点的编号存入对于位置的指针表中。

2)遍历索引表,从上到下,每一个关键字按照节点的先后顺序,将所有节点信息写入文件,叫做索引表文件,接着销毁索引表。

从优化策略可知,指纹的查询、插入与删除操作都是基于索引表文件,其复杂度为O(N),为常数级。

2.3 检索模型

基于2.2节的哈希表,改进的检索模型如图5所示。

图5 检索模型

检索过程描述如下:

1)进行音频指纹的提取查询,这里利用Philips指纹提取算法来实现。

2)按照先后顺序,每次从查询指纹中选取一个指纹作为查询候选指纹,利用构造哈希函数,将查询候选指纹映射成指针表的key。

3)根据key和key+1,计算出候选真实指纹集位置信息。

4)根据位置信息,从索引表文件中读取真实指纹集的信息进行匹配,如果匹配成功,继续计算对应的指纹块相似度,基于阈值判断是否相似,相似则返回查询成功信息,否则继续比较剩余的指纹集直到结束。

5)继续比较下一个查询候选指纹,重复第3)步和第4)步,直至结束。

最后,输出前Top-N最相似歌曲。

从查询过程可以看出,仅指针表存放在内存中,根据实际的内存情况,调整的指针表长度为232-N,可以全部放入内存,实现快速检索,从而实现提升Philips指纹检索系统的实用性。

3 实验结果与分析

本文通过实验评估改进算法性能。实验设计从3个方面进行评估:查询精度,查询速度和空间利用率,并与Philips研究做比较分析。

实验通用参数配置如下:

1)数据库,包括8 740段音乐片段,MP3和wav格式。

2)音乐的类型,包括流行音乐,古典音乐,民族音乐等。

3)实验算法参数设置,帧长0.37 frame/s;指纹块长度为256,大约3 s;相似阈值0.35。

3.1 查询精度的评估

为了评估查询精度,从某音乐网站下载免费音乐片段用于查询,实验分2组观察:

1)元音数据,未添加任何噪音,原版音乐。

2)噪音数据,观察噪音情况下,改进算法的性能变化。选择噪音场景为鼓掌、尖叫以及其他环境噪音,将噪音添加到查询音频中,信噪比为100 dB,属于轻度噪音级别。

3)服务器配置,32 GB内存,可用内存20 GB左右。

共选择100首歌曲用于评估,评估的数据结果如表2所示。

表2 查询精度 %

从表2结果可以看出,2种方面查询精度相同。事实上,2种查询的原理完全一样,从设计理论上也可以验证。从分享结果可知,改进的方法可以实现相同的精度,为后面的实验提供基础。

3.2 查询速度的评估

本文改进的算法目标是优化Philips内存使用,所以查询速度,主要观察普通PC下,改进算法的查询速度。

实验设置:

1)观察平均查询速度,通过增加歌曲数量观察查询速度的变化,这里仅仅考察元音数据。

2)PC配置:4 GB内存,可用内存1.6 GB。

最后,实验结果如图6所示。

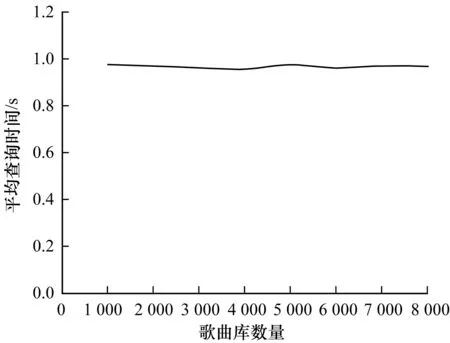
图6 评估查询效率

从图6可以看出,随着音乐数量的增加,查询速度一直在0.97 s附件波动,相对比较平稳变化。查询速度平稳的变化主要原因是由斐波那契数列优化效果。此外,针对查询效率,本文提出一个优化策略,构造2个哈希表,指针表存储索引表偏移信息;索引表存储真实指纹的位置信息。通过指针表可以快速访问索引表文件,定位真实指纹位置信息。索引表文件的优点是可以实现海量数据的快速访问。

3.3 空间利用率的评估

Philips检索算法的主要缺陷,就是内存消耗太大,本文针对这个缺陷提出改进。由于音乐数量较少,而Philips哈希表的长度太大,内存消耗改进的效果不言而喻,因此仅仅考察空间利用率性能,即基于相同的哈希表长度,考察斐波那契数列的作用。

将空间利用率定义(UR)为在哈希表中,已经利用的空占总空间的比例。UR为:

(6)

其中,UN代表已经占用的空间,L代表哈希表的总空间。实验结果如图7所示。

图7 空间利用率

从图7可以看出,提出的算法空间利用率显著优于Philips方法,即哈希值呈现良好的分布。可见,基于构造哈希函数和哈希表,实现了哈希值的较好分布,空间利用率得到提升。

4 结束语

本文针对Philips音频检索算法对内存消耗太大的缺陷,提出改进算法。利用斐波那契数列和右移运算,实现了新哈希函数的构造和哈希值分布的优化,并且可以灵活地调整哈希表的长度。为提高查询速度,提出优化策略。实验结果表明,改进的算法具有相同的查询精度,而且空间利用率显著提升,即解决了Philips内存消耗过大的问题。下一步将深入研究噪音环境,针对如何提高音频检索的精度和检索算法的健壮性展开研究。

[1] ZHAO Yong,ZHANG Aixin,LU Songnian.A Group-Based Fingerprinting Scheme for Digital Wholesale and Retail [J].China Communications,2014,11(10):126-135.

[2] DALIBOR M,MATTHIAS Z,CHRISTIAN B.Features for Content-based Audio Retrieval[J].Advances in Computers,2010,78:71-150.

[3] 牛宪华,曾柏森,陈思利.基于频域和时域差分的音频指纹算法研究[J].西华大学学报(自然科学版),2014,33(5):10-15.

[4] 孟建华,陈 宁.基于Gammachirp耳蜗能量谱特征提取的音频指纹算法[J].华东理工大学学报(自然科学版),2015,41(5):666-670.

[5] WANG A.An Industrial Strength Audio Search Algorithm[C]//Proceedings of International Conference on Music Information Retrieval.Baltimore,USA:[s.n.],2003:7-13.

[6] HAITSMA J,KALKER T.A Highly Robust Audio Fingerprinting System[C]//Proceedings of International Conference on Music Information Retrieval.Washington D.C.,USA:[s.n.],2002:107-115.

[7] 明建成,韩 威.基于音频指纹的压缩域音频识别方法研究[J].西华大学学报(自然科学版),2014,14(16):10-15.

[8] XIAO Q,SUZUKI M,KITA K.Fast Hamming Space Search for Audio Fingerprinting Systems[C]//Proceedings of International Conference on Music Information Retrieval.Washington D.C.,USA:[s.n.],2011:133-138.

[9] DAMGARD I B.A Design Principle for Hash Functions[C]//Proceedingsof Conference on the Theory and Application of Cryptology.Berlin,Germany:Springer,1989:416-427.

[10] BELLARE M,ROGAWAY P.Collision-resistant Hashing:Towards Making UOWHFs Practical[C]//Proceedings of the 17th Annual International Cryptology Conference.New York,USA:ACM Press,1997:416-427.

[11] AYDIN F,DOGAN G.Development of a New Integer Hash Function with Variable Length Using Prime Number Set[J].Balkan Journal of Electrical & Computer Engineering,2003,1(1):10-14.

[12] ULLANATT V.Summary Representation for Service Discovery Protocols [D].North Carolin,USA: North Carolina State University,2001.

[13] SHIU P,NIVEN I,ZUCKERMAN H S,et al.An Introduction to the Theory of Numbers[J].Mathematical Gazette,2013,39(328):401-405.

[14] MARKOWSKY G.Misconceptions About the Golden Ratio[J].The College Mathematics Journal,1992,23(1):2-19.

[15] DUNCAN R I.Application of Uniform Distribution to the Fibonacci Numbers[J].Fibonacci Quarterly,1967,5(5):137-140.