基于高维数据流的异常检测算法
,,
(苏州大学 计算机科学与技术学院,江苏 苏州 215006)
0 概述
异常检测旨在从数据集中快速有效识别异常点,在金融数据分析、网络安全、医学疾病与药物分析领域被广泛应用。基于无线传感网和GPRS技术,对物理世界进行感知,则是数据挖掘异常检测领域又一重要研究方向[1]。传统的异常检测算法主要分为基于统计的异常点检测算法、改进的基于距离的异常点检测算法、基于密度的局部异常点检测算法[2],它们主要基于统计学理论,以欧氏距离作为异常评判标准。
基于传感器技术的数据挖掘能从大量、模糊的复杂数据中提取出潜在的、有价值的信息,而且传感器网络数据多以高维形式存在,具有海量、异构有噪声、实时要求性高等特性,这使得传统的数据分析算法检测出异常点的效果不明显,而且时间复杂度过高,具有潜在的局限性。高维数据流的异常检测面临较多的挑战。
国内外已有大量的学者针对无线传感网的数据挖掘进行相关研究并提出一系列方法用于高维数据流的异常检测。如文献[3]采用K-means算法思想,比较传感器节点采集的数据点的相似度并划分聚类,根据数据点与聚类中心的距离区分正常数据与异常数据,但该方法采集的数据点维数有限,不适合高维数据的检测。文献[4]提出采用基于模式的聚类算法,分段取模式特征,并结合K最近邻算法计算局部异常因子。文献[5]提出一种快速数据流离群点检测算法FODFP-Stream,通过动态发现和维护频繁模式来计算高维类别属性数据点离群度实现快速有效检测,但针对数值属性和混合属性数据的异常检测缺乏一定的扩展性。
针对高维空间下的异常点检测,文献[6]提出基于角度的异常检测算法(Angle-based Outlier Detection,ABOD)[6]。在高维空间中,角度比距离更稳定,余弦角度方差一定程度上可以反映数据的异常度[6-7]。在此基础上,文献[8]提出了HODA算法,定义了方差异常因子和网格密度等相关概念,通过降维和网格划分处理数据集,最后根据剩余的网格计算异常因子ABOF。虽然该算法准确率较高,但是算法时间复杂度仍较高。
高维数据流是连续的时间序列值,正常情况下在一定范围内出现小幅度的波动。某一异常点的出现与上一条数据存在一定的偏差,或者从某一时间序列开始,数据点偏离最佳数据集[9]。针对高维数据流的这一特点,本文提出一种改进的基于角度方差的数据流异常检测算法。该算法根据采集的高维数据流特点,利用网格划分出最佳数据集网格和最近数据集网格提高算法的运行效率。
1 问题描述及相关定义
下面简要介绍相关知识:
定义1假设高维数据流是一种K元关系R={rt|rt∈S,t=1,2,…},其中,元组rt(t=1,2,…)连续到达[10],t为该数据点到达时间,K为数据的维度。
定义2假设给定一种Rd空间上的数据集S={X1,X2,…,Xi,…,Xn}以及一个样本点Xp∈S,随机选择一对样本点Xm,Xn∈S{Xp},θmpn为向量mp与pn的角度,所有θmpn的角度方差值为:
VOAp=Var[θmpn]=MOA2(p)-(MOA1(p))2
(1)
其中:
(2)
(3)
定义3最佳数据集网格是数据流的小规模数据流型。在数据空间中,由角度方差在阈值μ内的数据点被且标记为正常数据的数据点组建成网格。
基于物联网技术采集的数据流采集可以感知电梯运行整体状况。电梯数据流模型中有实时状态数据和维保特征、运行特征等,数据来源更丰富,潜在高阶特征多,更全面地反映电梯运行健康状况:
1)电梯基本特征包含了电梯基本信息,包括电梯使用年限和已使用年限、额定速度等。
2)电梯维保特征是电梯维保状况的重要体现,如电梯维保频次、平均维保时间等。
3)电梯运行特征主要包括当月故障次数、困人次数和用户投诉情况等。
4)电梯机械节点实时状态,这是电梯特征中最关键的特征。以传感器和通信技术为基础,感知电梯各重要机械节点的实时运行状态。
2 改进的高维数据流异常检测算法
本文利用数据集网格划分加快了ABOD算法的计算,同时通过实时更新网格的机制保证数据检测精度;基于此,针对电梯状态数据先进行预处理,对数据属性进行筛选,其次将本文改进算法运用于电梯数据流的异常分析。
实时数据流的检测需要算法具有较好的及时性和准确性。本文改进算法的主要思想为:根据数据分布对数据流进行划分,文献[8]通过对所有的数据点进行网格划分来过滤正常区域,但这一方法未考虑数据流的概念转移问题,在本文算法的执行过程中,实时维护一个最佳数据网格和最近数据网格,据此对最新采集的高维数据计算角度方差异常因子,使得历史数据流中部分数据参与角度方差因子的计算,计算代价小,满足实时性要求;对于算法检测出的异常点,分析导致数据异常的主要属性,确保算法对数据异常属性的识别能力。
如图1所示,计算正常网格和候选网格中数据点的异常因子,HODA算法认为角度方差异常因子小于阈值的数据点为异常点。
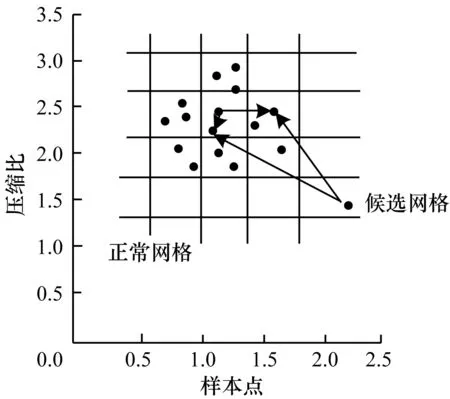
图1 数据点角度方差
算法高维数据流异常检测
输入最佳数据网格阈值μ,最佳数据网格尺度BL,最近数据网格尺度RL
输出异常数据集S
1.Best_grid→Ø,Latest_grid→Ø
2.for inputXiFrom Datastream,init grids
3.for all Diin best_grid,calculate the XiVOA
4.for allFiin Latest_grid,calculate the XiVOA
5.calculate the averageVOA according to the above VOA value.
6.if VOA of Xi<μ,label Xias normal
7.if number of Di>BL,dequeue the first record
8.else Di=DiU {Xi}
9.if number ofFi>RL,dequeue the first record
10.else Fi=FiU {Xi}
11.else S=S U {Xi}
12.end
其中,步骤3、步骤4是算法的核心步骤,以上步骤的流程如图2所示。

图2 算法流程
为使算法运行效率更高,在计算角度方差异常因子之前,算法先由样本值和最佳数据网格阈值筛选出最佳数据集区域。最佳数据集网格划分阈值是一个关键参数。在取不同值时,最佳数据网格抽象的结果相差很大。当过大时,网格划分粒度过大,网格中数据增加,从而加大了计算量,算法优化效果不明显。反之,当过小时,最佳数据集代表性不强。此时,虽然计算效率提高,但聚类效果也明显下降。
最佳数据集阈值μ、最佳数据集尺度BL和最近数据集尺度RL是影响算法精度的主要因素,而且不同的尺度和阈值对应于不同的算法精度。为了获得最优的尺度和阈值,算法需要进行大量的实际测试。一般而言,每种应用产生的数据集对应于一定的规律与特性,同时也对应了一组最优的权值和阈值[11]。大量实验结果表明,只要获得一组与数据集对应的最优权值和阈值,算法即可以获得较高的准确性。
3 基于改进算法的电梯异常数据检测
3.1 数据预处理
在高维数据流分析中,如何从大量复杂原始特征中去除影响因子小的相关特征,提取关键特征,对于提高检测精度和效率必不可少[12]。
1)RTS特征
传感器采集的电梯各机械部位实时特征在4大数据源中所占比重最大,也是最有价值的特征值。在本文项目中,通过传感器技术可以采集到的电梯特征值如图3所示,同一时刻采集电梯共19维特征。
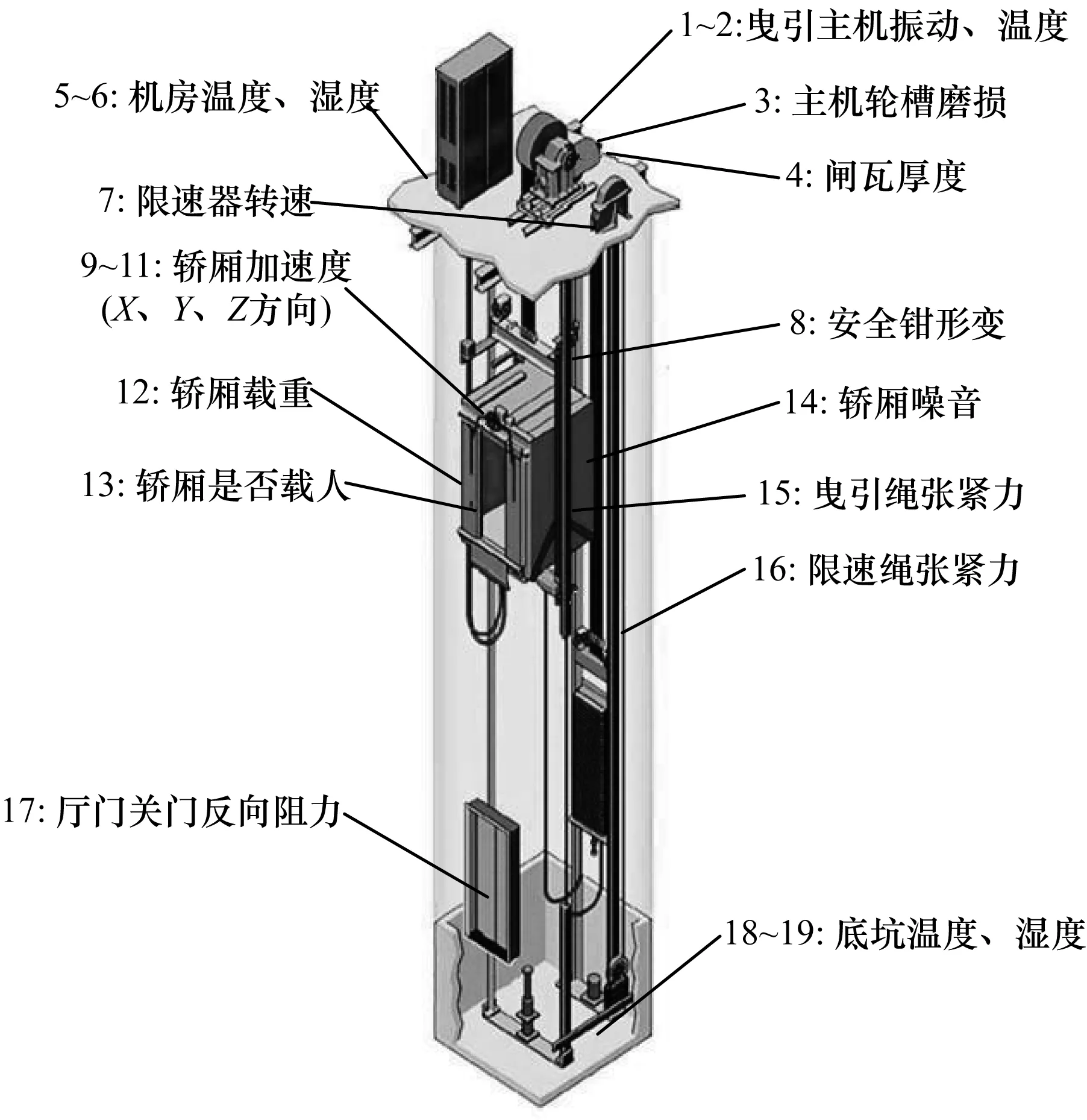
图3 电梯各部位实时特征值
2)MTS特征
维保特征是电梯检修和维护状态的体现。本文选择了比较重要的维保周期、维保项目、平均维保时长和维保满意程度等4个特征。
3)FD特征
电梯基本特征是对电梯主要特征的描述。根据关键质量指标[13]选择了额定载重、电梯层站门数、折余价值和日平均使用时间等4个关键特征。
4)RTD特征
电梯运行特征是指电梯故障统计特征,包括过去一周电梯故障次数、困人次数、被投诉次数和工单派发次数等,这是电梯重要异常特征历史值。
其中,RTS是无线传感网采集的电梯各关键部位实时数据流,后3类特征值是较为稳定的电梯特征值,以周为单位进行统计查询得到相关特征。
电梯部分状态特征如表1所示。

表1 电梯部分状态特征
3.2 电梯高维数据流异常检测
由于电梯数据包括实时数据流和维保特征、基本特征等较为稳定的数据值,本文将采集的电梯实时数据流进行初始化,将电梯实时状态数据Xi作为输入:
1)统计查询电梯本周的MTS、FD、RTD等特征值,并进行预处理。
2)实时采集数据流,获得一定的高维数据集样本,根据样本值和最佳数据集阈值进行初始化,从而构造初始最佳数据网格和最近数据网格。
3)传感器网络采集的即时状态数据Xi和小规模数据流型计算集实时计算该数据点的VOA值。
4) 基于VOA值和设定的最佳数据集阈值判断最新数据点的异常情况。
5)若为异常点,则纳入异常数据集并计算异常属性,分析导致异常的维度;若为非异常点,则按照先进先出法和最近数据集网格尺度对最近数据集网格进行更新。
4 实验结果与分析
本文方法采用的实验环境为计算机Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz,内存8.0 GB。开发平台为PyCharm 2015,采用Python语言和pandas等分析包对本文改进的算法和HODA算法进行比较,并对电梯运行状态的真实数据进行检测。
本文采用运行时间和准确率作为算法的评价指标[14],准确率是用来衡量算法的精度。
p=o/c
(4)
其中,o表示预测异常点集中真实异常点个数,c为算法检测到的异常点总数。
实验1采用入侵检测数据集KddCup99[15]作为测试数据集。该数据集具有高维的特性,这里分别选择其中的1 000条、 2 000条、3 000条、5 000条数据,其中异常记录为25条。
本文采用KddCup99数据集分析算法的及时性和有效性,进行以下实验:设置参数最优数据网格阈值μ为0.3,最佳数据集尺度BL为50,最近数据集尺度RL为30;采用ABOD算法、HODA算法与本文算法进行对比,其中HODA算法与本文算法的实验结果如表2、图4所示。
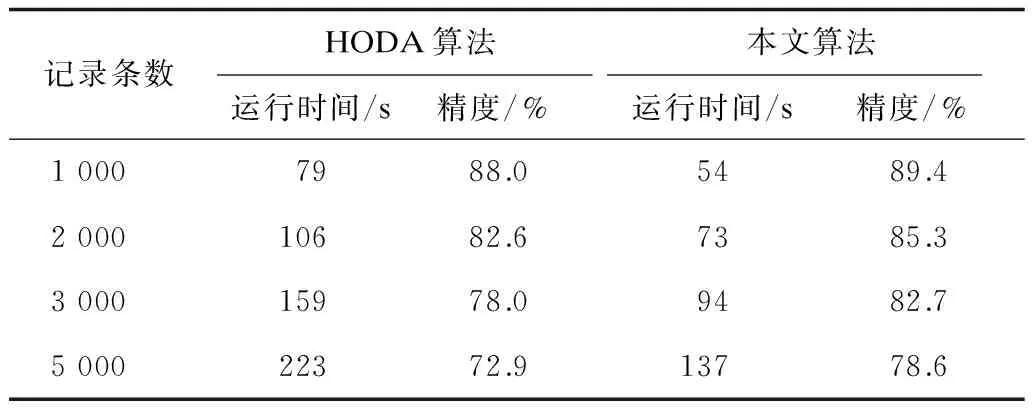
表2 2种算法实验结果分析

图4 不同算法精度对比
针对实验数据集,从表2和图4可以看出,当实验数据集增大时,在算法运行时间上,本文算法比HODA算法更有优势,原因在于HODA算法在计算异常因子时会重新分配数据网格,算法的计算复杂度加大。3种算法精度都呈下降趋势,但是相比HODA算法本文算法实验获得的最优参数能够保证对高维数据异常状态的识别能力,相比HODA算法保持较高的精度。
实验2使用昆山市某电梯公司2016年4月—2016年5月物联网平台数据作为实验数据来源,分布于电梯各机械部位的无线传感器节点,将采集到的电梯状态数据通过GRRS发送到服务器,其数据采集频率为2 s一次。
图5是2种算法在不同时刻的运行时间对比,随着电梯高维数据流的陆续到达,算法数据规模呈指数增长,可以看出本文异常检测算法运行所消耗时间均小于相同数据规模下的HODA算法。因为HODA算法在计算角度方差异常因子时需要实时对网格进行划分后筛选出候选网格,而本文算法维护2个最具代表的网格数据集,数据规模越大本文算法在其运行时间上的优势越明显。
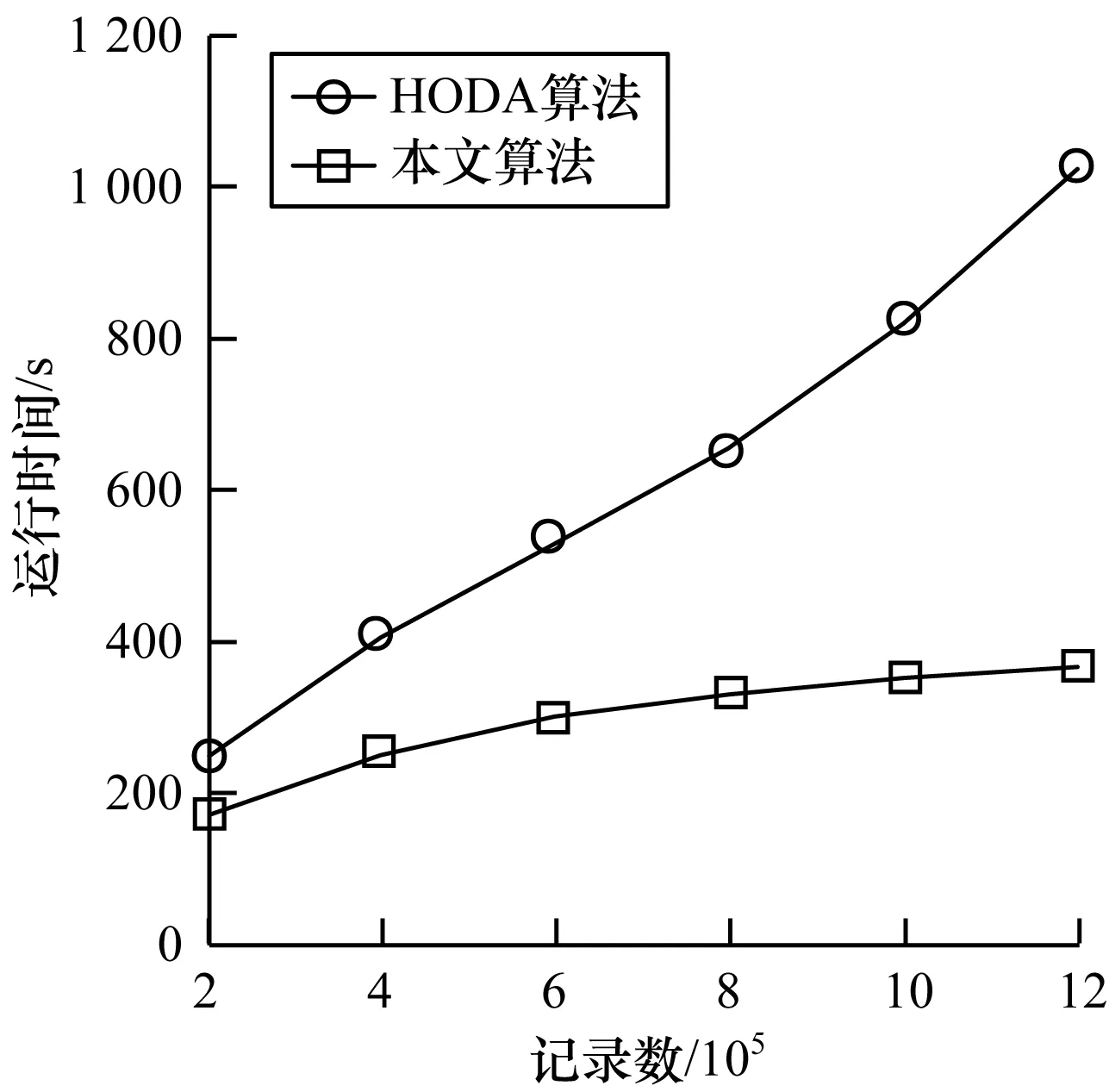
图5 电梯异常数据检测时间
查准率采用被检测出的实际异常点数目与检测到可疑异常点数目之比进行度量。实验过程中电梯产生12次不同程度的异常事件,根据图6中2种算法平均查准率的对比可知,本文算法的查准率要优于HODA算法。这是因为对于数据流中的最新数据点HODA算法需要重新进行网格划分,当数据集规模较大、维数较高时,该方法的候选网格增多,会将较多非异常的数据误以为是异常状态值。且本文算法采用最新数据集网格,可以有效地解决数据流的概念转移问题,使得算法的查准率得到保证。

图6 电梯异常数据查准率
5 结束语
本文基于角度分布的高维数据异常检测方法,提出一种改进的异常检测算法。在数据流检测过程中,对数据集进行重要网格划分和维护,降低角度方差计算代价,并且通过最近数据集的设定解决数据流中的概念转移问题。实验结果表明,该算法能有效识别高维数据流中的异常点,相比HODA算法,时间复杂度更低,适合于高维数据流的异常检测。如何根据数据流的特点对阈值自适应,是下一步研究的内容。
[1] 曹东磊,曹建农,金蓓弘.一种无线传感网络中事件区域检测的容错算法[J].计算机学报,2007,30(10):1770-1776.
[2] DING J,WANG L,SHEN D,et al.An Anomaly Detection System on Big Data[J].Natural Science Journal of Hainan Universdity,2015(1):121-127.
[3] 费 欢,李光辉.基于K-means聚类的WSN异常数据检测算法[J].计算机工程,2015,41(7):124-128.
[4] 凌 骏,尹博学,李 晟,等.基于监控数据的MySQL异常检测算法[J].计算机工程,2015,41(11):41-46.
[5] 周晓云,孙志挥,张柏礼,等.高维类别属性数据流离群点快速检测算法[J].软件学报,2007,18(4):933-942.
[6] KRIEGEL H P,VHUBERT M,ZIMEK A.Angle-based Outlier Detection in High Dimensional Data[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2008:444-452.
[7] PHAM N,PAGH R.A Near-linear Time Approximation for Angle-based Outlier Detection in High Dimensional Data[C]//Proceeding of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2012:877-885.
[8] 陈圣楠,钱红燕,李 伟.基于角度方差的多层次高维数据异常检测算法[J].计算机应用研究,2016,33(11):3383-3386.
[9] ZHANG Y,HAMM N,MERATNIA N.Statistics-based Outlier Detection for Wireless Sensor Networks[J].International Journal of Geo graphical Information Science,2012,26(8):1373-1392.
[10] 朴昌浩,黄 至,苏 岭,等.基于角度分布的高维数据流异常点检测算法[J].上海交通大学学报,2014,48(5):647-652.
[11] KRIEGEL H P,HUBERT M S,ZIMEK A.Angle-based Outlier Detection Inhigh-dimensional Data[C]//Proceedings of IEEE KDD’08.Washington D.C.,USA:IEEE Press,2008:444-452.
[12] 刘 靖.复杂数据类型的离群检测方法研究[D].广州:华南理工大学,2014.
[13] SIMUNDIC A.Quality Indicators[J].Biochemia Medica,2008,18(3):311-319.
[14] FELDMAN D,SCHIDT M,SOHLER C.Turning Big Data Into Tiny Data:Constant-sizecoresets for K-means,PCA and Projective Clustering[C]//Proceedings of the 24th Annual ACM-SIAM Symposium on Discrete Algorithms.Washington D.C.,USA:IEEE Press,2013:1434-1453.
[15] 陈冠华,马秀莉,杨冬青,等.面向高维数据的低冗余Top-k异常点发现方法[J].计算机研究与发展,2010,47(5):788-795.

