稀疏数据中基于高斯混合模型的位置推荐框架

,

(1.四川大学 计算机科学与技术学院,成都 610000; 2.南京晓庄学院 新闻传播学院,南京 210017)

0 概述

在基于位置社交网络的服务(如Foursquare、Gowalla、Mirco-blogging、大众点评网等)中,用户可以分享自己的地理位置信息以及与位置相关的内容。基于位置社交网络的位置推荐已成为热点研究[1-4]。

目前,有很多学者对位置推荐进行研究。一些学者采用协同过滤的方法进行位置推荐,对于相似的人可能会有相似的位置偏好。例如,文献[5]提出了Flap系统,它可推断社交纽带并重建整个朋友关系网络,最后预测用户的细粒度位置从而进行位置推荐。然而此类研究忽视了用户的移动模式因素。也有一些学者采用概率模型的方法进行位置推荐,每个人在不同区域签到符合一定的概率分布规律。例如,文献[6]利用Twitter中的地理位置信息、发表时间、用户ID以及文本信息以发现用户的时空活动行为模式,从而预测用户在不同区域签到的概率并进行位置推荐。然而此类研究往往需要建立在健全数据信息的基础上,否则难以实现有效推荐。

针对稀疏数据,本文基于高斯混合模型(Gaussian Mixture Model,GMM)构建位置推荐框架GMMSD。考虑用户的移动模式预测用户在所有区域签到的概率分布,并结合用户之间的协同影响和个人的移动性规律进行位置推荐。

1 相关工作

位置推荐方法主要分为2类:协同过滤和概率模型。

1.1 协同过滤

文献[7]提出融合矩阵分解(Matrix Factoriza-tion,MF)模型,首先捕捉地域影响力,然后考虑社交信息建立矩阵分解模型,从而进行个性化位置推荐。文献[8]提出SeqRWR方法动态选择在每个时间片对目标用户最有影响力的N个朋友,然后利用所构建的TSB模型对朋友影响力的特征建模,在每个时间片对用户进行位置推荐。文献[9]构建IRenMF方法探究周边地理位置的特征,学习用户和位置的潜因子以提高位置推荐的准确度。文献[10]构建GeoMF模型,首先利用所提的加权矩阵分解解决隐式反馈协同过滤POI推荐的稀疏性问题,然后将空间聚类现象融入到矩阵分解模型中以提高推荐性能。文献[11]实现了基于用户偏好并且时间敏感的推荐系统。该系统考虑了位置的流行度、用户的偏好、用户的朋友、用户访问位置的时间特征4个因素,为用户做特定时间的位置推荐。文献[12]提出了基于位置和偏好感知的推荐系统。该系统同时考虑了用户个人偏好和本地专家的意见。

不同于以上的协同过滤方法,本文框架考虑用户的移动模式,能预测用户在所有区域签到的概率分布并进行位置推荐。

1.2 概率模型

文献[4]提出了LORE方法。该方法从用户签到位置序列中挖掘序列模式并构建马尔科夫链,最后结合地理和社交影响建立模型从而进行位置推荐。文献[6]利用微博中的内容、用户ID、时间、地理位置信息进行建模,构建W4模型从而为用户进行位置推荐。文献[13]构建PMM模型,利用用户周期性移动特性在不同时间段为用户进行位置推荐。

本文框架考虑相似用户的协同作用对推荐性能的影响,并能在稀疏数据集上进行有效推荐。

2 GMMSD框架

2.1 工作原理

本文位置推荐框架的工作原理如下:

1)将用户历史签到数据按4个时间段分为4个部分。

2)对城市空间进行网格划分和序列化,经过噪声过滤后再根据用户的时间片签到数据得到用户-区域矩阵。

3)运用矩阵分解填充稀疏值,得到分解后的用户-区域矩阵。

4)采用K-Means聚类算法得到每个用户的签到聚类中心。

5)利用高斯混合模型建模,针对每个区域,计算二重积分得到用户在区域签到的概率。

6)Top-k概率值对应的区域即为推荐位置。

2.2 数据预处理

定义1(区域) 将整个城市空间S划分成N个相同的单元正方网格r(例如:200 m×200 m),该单元正方网格称为区域。每个经纬度对都会映射到唯一的区域。

定义2(区域序列化) 将N个单元正方网格区域r横向展开为n元有限序列R=(r1,r2,…,rn),该过程称为区域序列化。序列R称为区域序列,序列元素值表示所有用户在该区域签到的次数。

定义3(噪声过滤) 将区域序列中元素值为0的元素去掉的过程称为噪声过滤。

定义4(签到区域序列) 用户到噪声过滤后区域序列对应的区域签到的次数排列称为签到区域序列。

图1描述了数据预处理的过程,其中主要包括4个步骤:1)将城市空间划分为N个区域;2)区域序列化;3)噪声过滤;4)生成签到区域序列。

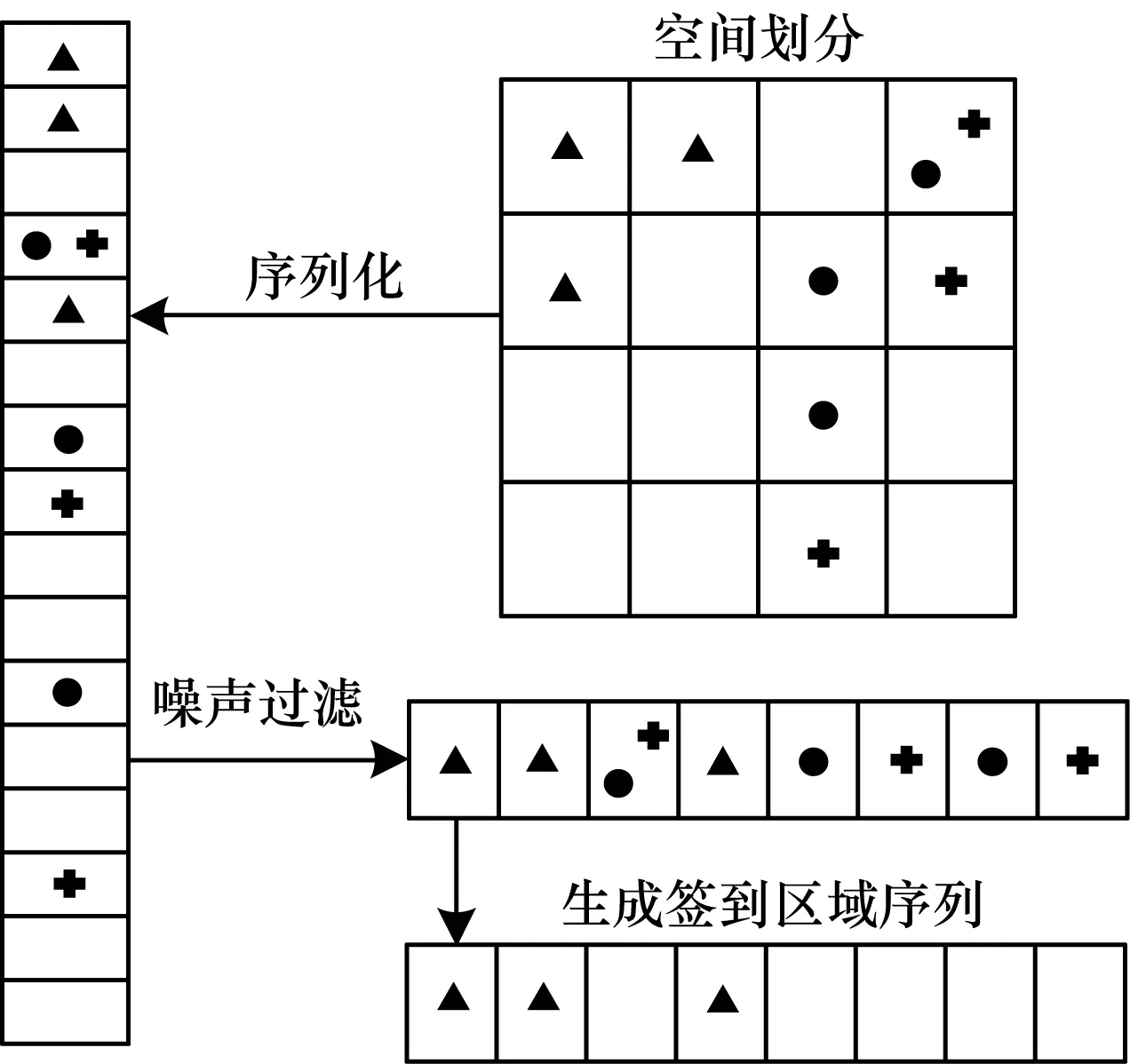
图1 数据预处理过程

2.3 稀疏数据处理

根据用户签到数据所得到的每个用户的签到区域序列往往是稀疏的。本文采用矩阵分解的方法予以解决。用户-区域矩阵定义如下:

定义5(用户-区域矩阵) 根据每个用户的签到数据,得到每个用户的R元签到区域序列。U个用户的签到区域序列构成一个用户-区域矩阵CU×R。矩阵元素值Cij表示用户i到区域j签到的次数。

矩阵分解假设每个用户的特征都可以由若干个因子进行刻画,而每个区域的特征同样可以使用相同数量的因子加以表示。当一个用户的特征和一个区域的特征相吻合时,就认为这个用户会以高频次去该区域,反之亦然。矩阵分解目标就是把用户-区域矩阵C分解为用户因子矩阵P和区域因子矩阵Q的乘积。一般表示为:

C≅PQT

(1)

其中,P∈U×D,Q∈R×D,D为刻画每个用户或每个区域特征的因子数。一般D的取值远小于U或R。用户在区域签到的真实频次和预测频次之间的差值e服从正态分布,即e～N(0,σ2),其等价于当用户-区域矩阵C非常稀疏时,就会出现过拟合问题。为降低模型的过度拟合,本文采用正则化的方法,最小化以下目标函数:

其中,λ为正则项的权重,称为惩罚参数。

下面使用梯度下降法进行求解。获得用户和区域因子矩阵P和Q后,使用式(2)计算用户u出现在区域r的频次:

(2)

此处梯度下降法的具体推导不再赘述,用户因子矩阵P和区域因子矩阵Q的更新公式如下:

Pud=Pud+η·(eur·Qrd-λ·Pud)

(3)

Qrd=Qrd+η·(eur·Pud-λ·Qrd)

(4)

梯度下降法中最小化的具体步骤见算法1。

算法1矩阵分解(MF)

输入用户-区域矩阵CU×R,潜因子数D,惩罚参数λ和学习率η

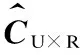
1.初始化P、Q;

2.REPEAT

3. FOREACH用户-区域对(u,r)∈P

5. 计算预测频次误差eur;

6. 依据式(3)更新用户因子向量Pu;

7. 依据式(4)更新区域因子向量Qr;

8. END FOREACH

9.UNTIL满足停止条件

2.4 高斯混合模型

即使用户移动具有多样性,但是由于用户偏好和地理条件的限制,用户移动会呈现一定的模式[13]。为提高预测的性能,本文引入高斯混合模型来研究用户的移动模式。

用户的签到情况往往是围绕几个中心区域分布的,通常需要利用多个高斯过程,即高斯混合模型来表示。用户的签到样本数据集R={r1,r2,…,rn}符合该用户的移动模式。这里,区域r由该区域的中心经纬度表示,即r=(x,y),其中x为该坐标点的纬度,y为该坐标点的经度。GMM模型公式如下:

(5)

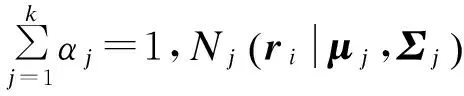
(6)

通常采用EM算法逐步迭代逼近最大值对参数进行求解。

(7)

EM算法的M步:更新参数φj=(αj,μj,Σj)。

(8)

(9)

(10)

算法2高斯混合模型(GMM)

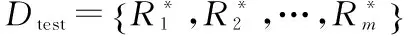
输出用户在测试集中每个区域签到的概率、推荐均方根误差RRMSE和平均绝对误差MMAE

1.FOR u←1 TO m /*循环每个用户,已知该用户的训练签到样本数据集Ru={r1,r2,…,rn}*/

2.利用K-Means算法确定k个聚类中心;

3.初始化GMM的模型参数Φ;

4. REPEAT

5. FOR i←1 TO n

7. END FOR

8. FOR j←1 TO k

9. 依据式(8)更新αj;

10. 依据式(9)更新μj;

11. 依据式(10)更新Σj;

12. END FOR

13. UNTIL满足停止条件

15. 将式(5)作为被积函数计算二重积分,得出用户出现在测试集中每个区域的概率;

16. 计算每个用户的推荐误差eru和emu;

17. END FOR

20.END FOR

本文结合矩阵分解和高斯混合模型建立的位置推荐GMMSD框架,相比于矩阵分解模型考虑了用户的移动模式,使用户的签到情况更符合用户真实的移动规律;相比于高斯混合模型考虑了相似用户的协同影响,能在稀疏数据上进行有效推荐。

3 实验与结果分析

3.1 数据集

本文使用基于位置社交应用BrightKite和Gowalla中纽约城市的签到数据(具体信息如表1所示),从中随机选择30%的用户签到记录训练模型,再从剩余70%的用户签到记录中按时间选取每个用户前70%的签到记录作为模型参数验证数据集,剩余的30%数据作为测试集。

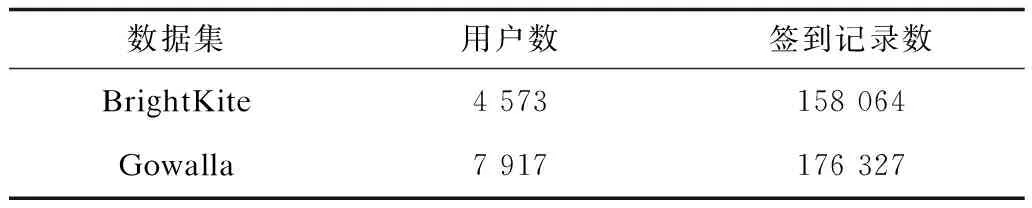
表1 实验数据集

3.2 评价指标

为评价不同方法的推荐性能,本文使用2个评价指标,即均方根误差RRMSE和平均绝对误差MMAE,分别如式(11)和式(12)所示。

(11)

(12)

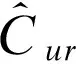
3.3 对比算法

本文将GMMSD框架和以下方法进行对比:

1)协同过滤算法(CF)[11]:相似的用户间可能会有相同的位置偏好。该算法基于社交关系,用户会以很大概率到朋友去过的区域签到。

2)张量分解算法(TD)[14-15]:针对用户签到的特征集,将其集成到一个三维张量中,三维分别是用户、区域和时间。运用张量分解填充稀疏值,得到特定时间值的用户区域概率矩阵。

3)矩阵分解算法(MF)[7,9,16]:该算法是本文提出框架的基础,它可以很好地解决数据稀疏性问题,对用户-区域矩阵,运用该算法计算用户到每个区域的频次,最后归一化处理得到每个用户到不同区域的概率,Top-k概率值对应的区域即为推荐位置。

4)高斯混合模型(GMM)[17-18]:根据用户的签到数据对用户进行移动性建模,然后计算二重积分,得到用户在不同区域签到的概率，从而进行位置推荐。

3.4 参数调整

在本文框架中,本文将用户历史签到数据按4个时间段(T1～T4)划分为4个部分。其中:T1表示时间段0:00—6:00;T2表示时间段6:00—12:00;T3表示时间段12:00—18:00;T4表示时间段18:00—24:00。通过实验设置学习率η=0.001,惩罚参数λ=0.005。此外,本文还需要设置2个参数,即潜因子个数D和聚类中心个数K。随机选取每个用户30%的签到记录训练参数。在4个时间段内参数调整对推荐性能的影响如图2～图5所示。

图2 时间段T1内参数调整对推荐性能的影响

图3 时间段T2内参数调整对推荐性能的影响

图4 时间段T3内参数调整对推荐性能的影响

图5 时间段T4内参数调整对推荐性能的影响

图2～图5显示了在2个验证数据集下不同时间段设置不同的聚类个数时RRMSE随潜因子个数变化的结果。为了使本文所提的GMMSD框架的推荐性能够达到最优,即使RRMSE的误差值最小,因此,通过观察图2～图5,本文将参数调整如表2所示。

表2 参数调整结果

3.5 实验结果

本文比较了4种方法(CF、TD、MF和GMMSD)的推荐性能。每种方法的均方根误差和平均绝对误差如图6～图7所示,可以看到GMMSD的推荐性能优于当前其他方法。为验证用矩阵分解填充数据的合理性,本文选取了相对较稠密的用户签到记录进行实验,比较2个数据集下的GMM和GMMSD推荐误差情况,如图8所示。

图6 均方根误差对比

图7 平均绝对误差对比

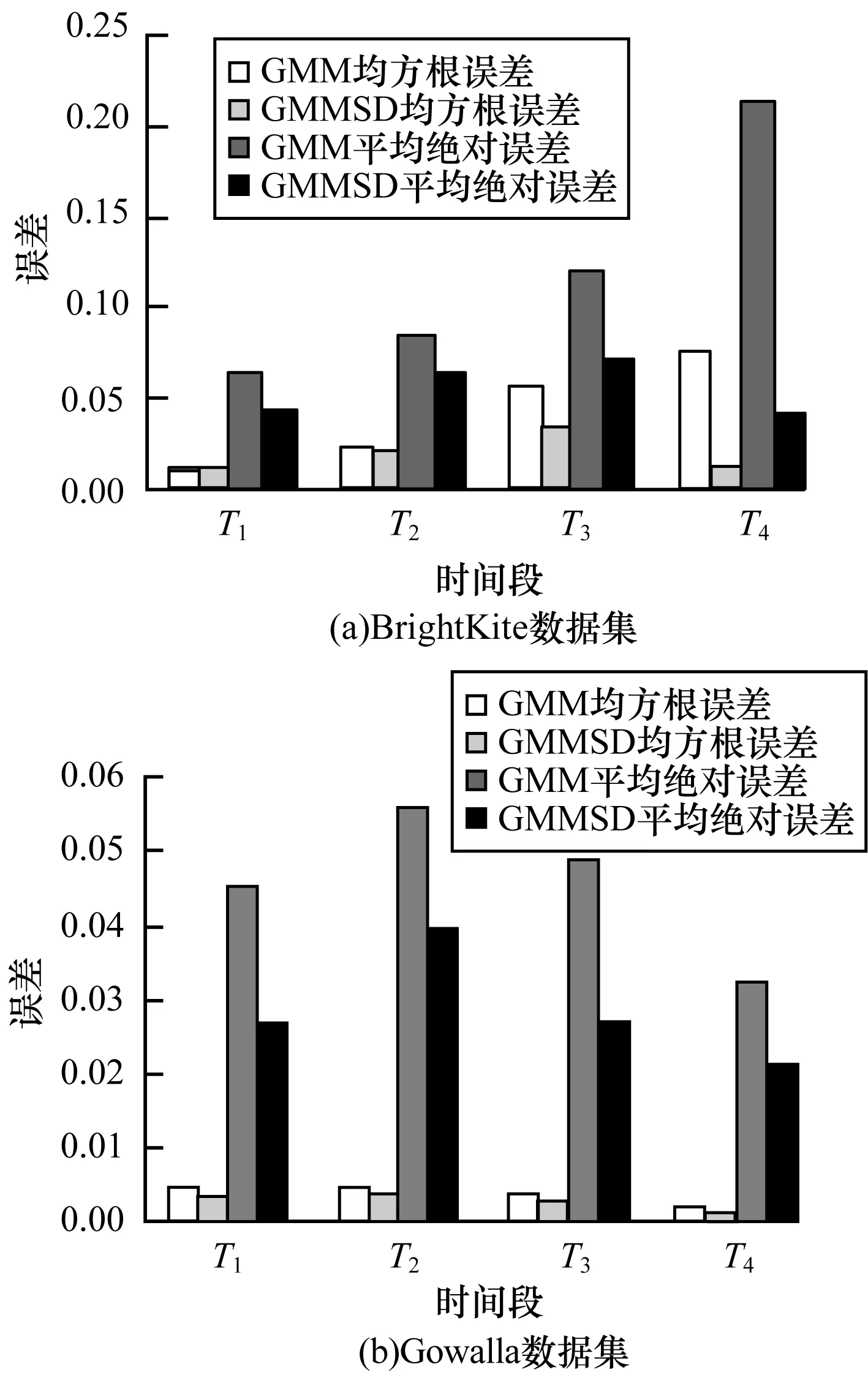
图8 GMM和GMMSD框架的推荐误差对比

由上述结果可知，CF面临着冷启动问题,无法对没有社交关系的新用户进行位置推荐。而TD和MF都没有考虑用户的移动模式,分解后的签到情况不符合用户的移动性规律。GMM只考虑了用户个体的移动性,没有考虑社会信息的影响并且该模型不适用于稀疏数据。而GMMSD性能较优的原因为:GMMSD同时考虑了相似用户的协同推荐和用户的移动模式,并能在稀疏数据上进行有效推荐，因此其性能较优。

4 结束语

本文构建一种稀疏数据中基于GMM的位置推荐框架。该框架结合了矩阵分解和高斯混合模型的优点,同时考虑了相似用户的协同推荐和用户个体的移动模式。首先将用户签到数据按时间段分片,再对城市空间进行区域划分和序列化,经过噪声过滤后得到用户-区域矩阵;然后利用矩阵分解建模用户之间的协同关系,在一定程度上缓解了数据稀疏问题;最后使用K-Means算法找到聚类中心并采用高斯混合模型计算每个用户出现在不同区域的概率,从而进行位置推荐。在真实数据集上的实验结果表明,本文框架考虑了社会信息和用户个体移动规律的共同影响,可在稀疏数据上进行有效位置推荐,并且准确度较高。后续研究将考虑加入社交网络信息,以进一步提高推荐准确度。

[1] RAHIMI S M,WANG X.Location Recommendation Based on Periodicity of Human Activities and Location Categories[M]//PEI J,TSENG V S,CAO L.Advances in Knowledge Discovery and Data Mining.Berlin,Germany:Springer,2013:377-389.

[2] JIE B,YU Z,WILKIE D,et al.A Survey on Recommendations in Location-based Social Networks[J].GeoInformatica,2015,19(3):525-565.

[3] ZHANG J,CHOWMEMBER C,LI Y.iGeoRec:A Personalized and Efficient Geographical Location Recommendation Framework[J].IEEE Transactions on Services Computing,2015,8(5):701-714.

[4] ZHANG J D,CHOW C Y,LI Y.LORE:Exploiting Sequential Influence for Location Recommendations[C]//Proceedings of the 22nd ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.New York,USA:ACM Press,2014:103-112.

[5] SADILEK A,KAUTZ H,BIGHAM J P.Finding Your Friends and Following Them to Where You Are[C]//Proceedings of the 5th International Conference on Web Search and Web Data Mining.Seattle,USA:DBLP,2012:723-732.

[6] YUAN Q,CONG G,MA Z,et al.Who,Where,When and What:Discover Spatio-Temporal Topics for Twitter Users[C]//Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2013:605-613.

[7] CHENG C,YANG H,KING I,et al.Fused Matrix Factorization with Geographical and Social Influence in Location-based Social Networks[C]//Proceedings of the 26th AAAI Conference on Artificial Intelligence.Toronto,Canada:AAAI Press,2012:17-23.

[8] JIA Y,WANG Y,JIN X,et al.Location Prediction:A Temporal-Spatial Bayesian Model[J].ACM Transactions on Intelligent Systems & Technology,2016,7(3):31.

[9] LIU Y,WEI W,SUN A,et al.Exploiting Geographical Neighborhood Characteristics for Location Recom menda-tion[C]//Proceedings of the 23rd ACM International Conference on Information and Knowledge Management.New York,USA:ACM Press,2014:739-748.

[10] LIAN D,ZHAO C,XIE X,et al.GeoMF:Joint Geographical Modeling and Matrix Factorization for Point-of-Interest Recommendation[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2014:831-840.

[11] ZHANG S,REN K.User Preferences-based and Time-sensitive Location Recommendation Using Check-in Data[J].Journal of Computer & Communications,2015,3(9):18-27.

[12] BAO J,ZHENG Y,MOKBEL M F.Location-based and Preference-aware Recommendation Using Sparse Geo-social Networking Data[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems.New York,USA:ACM Press,2012:199-208.

[13] CHO E,MYERS S A,LESKOVEC J.Friendship and Mobility:User Movement in Location-based Social Networks[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.San Diego,USA:DBLP,2011:1082-1090.

[14] ZHONG Y,YUAN N J,ZHONG W,et al.You Are Where You Go:Inferring Demographic Attributes from Location Check-ins[C]//Proceedings of the 8th ACM International Conference on Web Search and Data Mining.New York,USA:ACM Press,2015:295-304.

[15] ZHENG V W,CAO B,ZHENG Y,et al.Collaborative Filtering Meets Mobile Recommendation:A User-centered Approach[C]//Proceedings of 24th AAAI Conference on Artificial Intelligence.Atlanta,USA:AAAI,2010:236-241.

[16] 陈 芸,董西伟,荆晓远.联合混合范数约束和增量非负矩阵分解的目标跟踪[J].计算机工程,2015,41(12):260-264.

[17] 乔少杰,金 琨,韩 楠,等.GMTP:基于高斯混合模型的轨迹预测算法[J].软件学报,2015,26(5):1048-1049.

[18] 冀续烨,陈 明,冯国富,等.一种多模型协同的目标提取方法[J].计算机工程,2015,41(5):254-258.