基于局部与全局优化的双目视觉里程计算法

,,

(1.中国科学院上海微系统与信息技术研究所,上海 200050; 2.中国科学院大学,北京 100049)

0 概述

实时精确的自我定位是移动机器人实现自动导航的关键。视觉里程计[1]利用一个或多个摄像机获取图像序列并计算移动机器人的相对运动位姿,是一种相对定位的方法。与传统的轮式里程计相比,视觉里程计不受车轮打滑或路面不平等环境限制,且获取的视觉信息可用于避障和目标识别等视觉应用,具有更高的鲁棒性和更广的应用场景。

早期针对视觉里程计的研究都服务于星球探测车。文献[2]采用单目相机设计了一种“滑动立体”的装置,每当机器人停下时,相机水平滑行并等距拍摄9帧图像,然后通过三角测量法重建特征点的三维坐标,并使用这些三维点求解运动信息。在文献[2]研究的基础上,文献[3]使用双目立体视觉系统,并把重建的三维点的协方差矩阵用于运动估计,一定程度上提高了精度。文献[4]正式提出了Visual Odometry(VO),实现了鲁棒去除外点的实时VO系统,并首次在数百米距离上对VO算法进行了测试。后期VO的总体框架基本依照文献[4]方法,通过不断改进特征提取算法、特征匹配和跟踪算法、运动估计算法等,来获取更准确、快速、鲁棒的定位结果。视觉里程计最成功的应用是火星探测机器人“勇气号”和“机遇号”[5],它们采用的视觉里程计系统在火星上出色地完成了任务,为视觉里程计的发展带来极大动力。近年来视觉里程计开始被广泛应用在室内外导航、自动驾驶、增强现实(Augmented Reality,AR)等领域。

根据所用的传感器不同,视觉里程计可以分为单目、双目和RGBD。单目视觉里程计缺少尺度信息,不能获得绝对的位置信息;RGBD视觉里程计受深度相机的影响较大,深度误差和有效距离限制导致其自我定位精度较低;双目视觉里程计能够通过左右相机立体匹配获取深度信息,恢复机器人的绝对的位置信息并且精度较高。

按照深度信息重建的方式,双目视觉里程计又可以分为基于特征的方法[6]和直接法[7]。基于特征的方法通过提取图像的特征点进行特征匹配和稀疏三维重建,实时性较好;直接法对图像中的所有像素进行匹配,得到稠密的三维重建点云,很难保证实时性。因此,本文从实时性的角度考虑,设计基于特征点的双目视觉里程计。

视觉里程计的帧间运动估计存在误差,并且这种误差会累积,如何减小这种误差提高定位精度成为视觉里程计的研究重点,可以根据是否引入概率模型将其分为基于概率的方法和基于非概率的方法。基于概率的方法主要有基于扩展卡尔曼滤波器(Extended Kalman Filter,EKF)[8]的方式和基于粒子滤波器(Particle Filter,PF)[9]的方式等。基于概率的方法受噪声分布影响大,会带来非线性误差,在大规模场景下很难保证精度和鲁棒性。基于非概率的方法比较著名是基于关键帧的单目即时定位与地图构建算法PATM[10],该算法是非概率方法的基本框架。

本文设计一种基于特征点的双目视觉里程计算法,根据关键帧的关系,针对帧间运动估计进行局部优化,并采用回环检测对累积误差进行全局优化。

1 基于特征点的双目视觉里程计

基于特征点的双目视觉里程计首先在双目相机获取的左右图像上进行特征点匹配,通过匹配结果计算特征点深度信息;再根据前后帧的特征点跟踪进行运动估计求解当前帧的位姿,包括旋转矩阵R和平移矩阵T。

1.1 双目相机模型

相机模型使用针孔模型,双目相机在使用之前会经过立体标定[11],完成畸变矫正和平行校正。经过标定后的双目相机模型如图1所示。

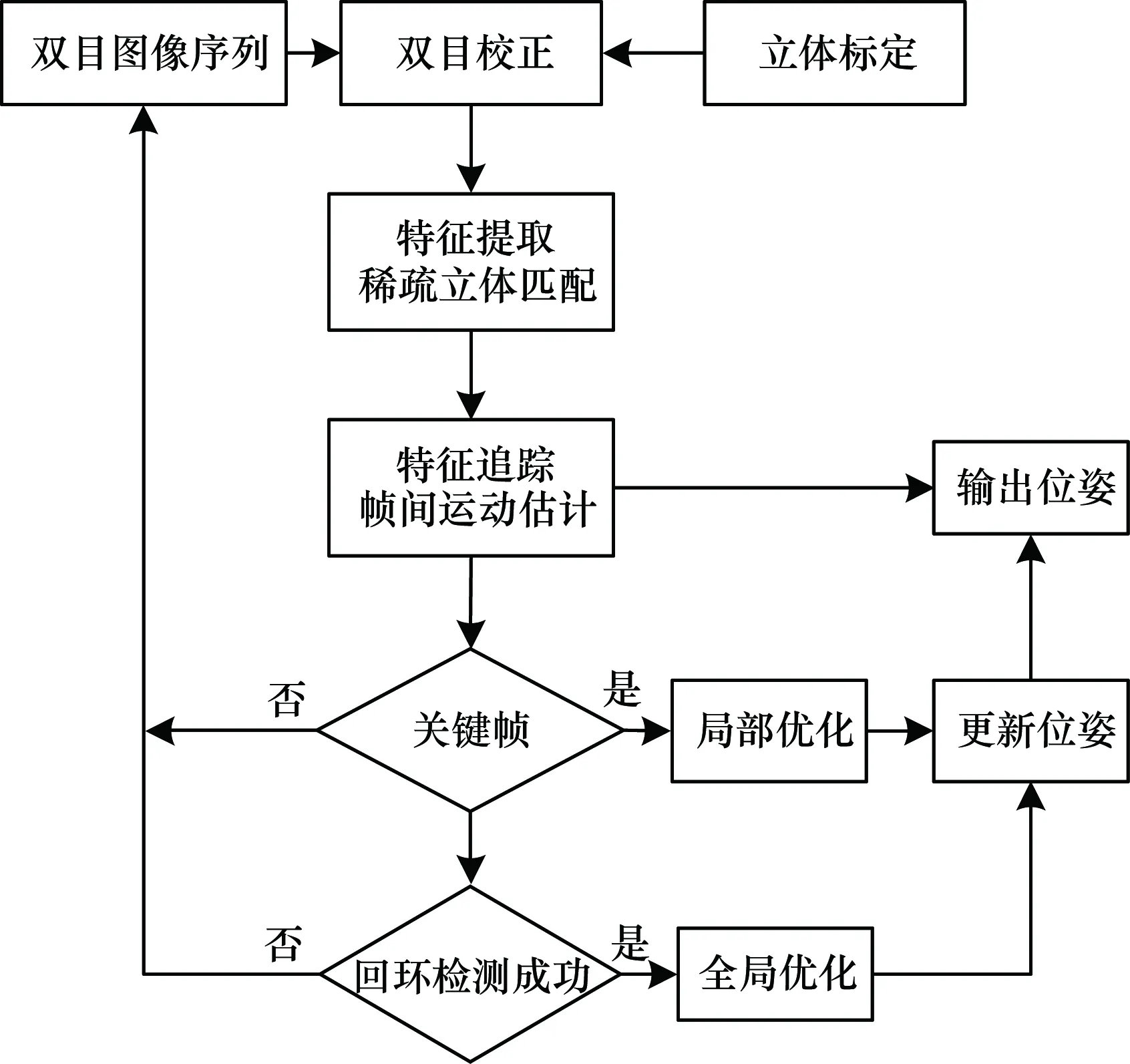
图1 算法整体流程

1.1.1 坐标系定义

摄像机坐标系:OciXciYciZci(i=1,2)。i=1表示左相机;i=2表示右相机;光轴方向Oc1Zc1和Oc2Zc1平行;光心之间相距Oc1Oc2=Tx表示基线。

图像坐标系:Oiuivi(i=1,2)。以像素为单位,左右相机具有相同的主点坐标(u0,v0)。

世界坐标系:OwXwYwZw。以左相机的摄像机坐标系为世界坐标系,并且第1帧图像的摄像机坐标系作为全局的世界坐标系,所有图像序列的位姿均相对于此世界坐标系表示。

1.1.2 投影模型与三维重建

世界坐标系中的点P(xw,yw,zw)投影到双目相机中得到左右图像中的P1(u1,v1)和P2(u2,v2)。设相机的内参为K,以左相机为追踪相机,则在齐次坐标系下投影方程表示为:

(1)

其中,s为比例因子,设为1。

对于空间中点P,通过三角计算恢复三维世界坐标示意图,如图2所示。

图2 双目相机模型图

P点在左右图像中的视差d=u1-u2,由三角关系可得:

(2)

将式(2)代入式(1),得到:

(3)

1.2 特征点提取与匹配

双目视觉里程计中的特征点匹配包括左右图像之间的稀疏立体匹配和帧间运动的特征追踪。为得到准确的特征点三维坐标,需要特征点算子具有可重复性和稳定性,包括光照不变性、旋转不变性、尺度不变性等,同时兼顾实时性。本文选择了一种基于GPU的加速尺度不变特征变换(Scale Invariant Feature Transform,SIFT)[12]算法SiftGPU[13]。SiftGPU缩短了SIFT算法的时间消耗,使其用于实时图像处理成为可能。SIFT算子是一种提取局部特征的算法,在尺度空间寻找极值点,提取位置、尺度、旋转不变量,并对视角变化、仿射变换、噪声也保持一定程度的稳定性。

获取左右图像的SIFT特征点后,采用特征向量的欧式距离作为相似性度量。对于立体匹配,极线校正后的图像匹配点基本处于同一行。对每个特征点,搜索其在另一幅图像中同一行和相邻2行的特征点计算欧式距离。比较每组特征的最近和次近距离的比值,当比值小于给定阈值,最近距离点判为匹配点,否则判为无效匹配点。降低阈值能提高匹配精度,增大阈值能获得更多的匹配点。本文通过对大量变换场景的左右图像匹配实验,选择0.6作为匹配阈值。分别以左右图为基准进行匹配,满足左右一致性才能成为为正确的匹配点。帧间运动的特征追踪以左图为基准,需要遍历更多的特征点,匹配准则和稀疏立体匹配相同。

1.3 增量式的运动估计

每一帧含有左右2张图像,以左图为基准,经过左右立体匹配和前后帧间特征追踪之后,得到了上一帧Ik-1和当前帧Ik的3D坐标匹配点集。假设从Ik-1到Ik相机经过旋转矩阵R和平移矩阵T,如图3所示。

图3 三维重建示意图

1.3.1 帧间运动估计求解

(4)

由于每一组匹配点存在误差(如式(5)所示),因此通过3D到3D的匹配点集求解旋转矩阵R和平移矩阵T,使所有匹配点的误差平方和最小化(如式(6)所示)。

(5)

(6)

求解上述方程,首先对3D匹配点集坐标分别去质心化,令两组匹配点集质心分别为:

(7)

因此,去质心后的匹配点坐标为:

(8)

将式(8)代入式(6)并展开得:

(9)

式(9)表示的优化问题可以等价于式(10)和式(11):

(10)

‖p′-Rp-T‖2=0

(11)

R=UVT

(12)

将式(12)代入式(11)得到:

T=p′-UVTp

(13)

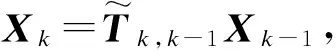
(14)

双目视觉里程计通过这种增量的方式从第1帧开始不断获得每帧相对于第1帧的位姿,实现定位的功能。

1.3.2 RANSAC运动估计

由于帧间运动的特征追踪存在误匹配点,错误的匹配点会导致式(10)的求解误差增大。为降低帧间错误匹配点给运动估计带来的影响,本文采用随机采样一致性方法(RANSAC)[15]去除误匹配点。主要步骤如下:

1)从匹配点集中随机选择m(m≥3)个匹配点,利用1.3.1节的求解方法求解初始R、T。

2)根据初始R、T按式(5)计算误差,如果小于给定阈值,该匹配点判断为内点,否则为外点。

3)重复上述步骤S次,找到内点数量最多的点集。

4)使用上述内点集重新计算R、T,并且剔除外点内的匹配点。

2 局部位姿优化

上述双目视觉里程计的运动估计只用了2帧之间的特征匹配,帧间约束较少,当2帧匹配点较少或误匹配太多时,计算出的位姿误差较大。本文在上述视觉里程计的基础上提出了一种基于可变滑动窗口的局部优化方法,增加帧间约束,提高帧间运动估计的精度和鲁棒性。

2.1 关键帧与非关键帧

为了提升计算效率,本文算法将图像序列分为关键帧和非关键帧。每个非关键帧和上一个关键帧一一对应,非关键帧的位姿相对于该关键帧表示,关键帧的位姿相对于第一个关键帧即全局世界坐标系表示,如图4所示。其中,第1帧设为关键帧,每隔fps帧设一个关键帧。由于旋转过程中图像变换过快,如果当前帧相对于关键帧新出现的特征点占比超过10%,则当前帧设为关键帧。

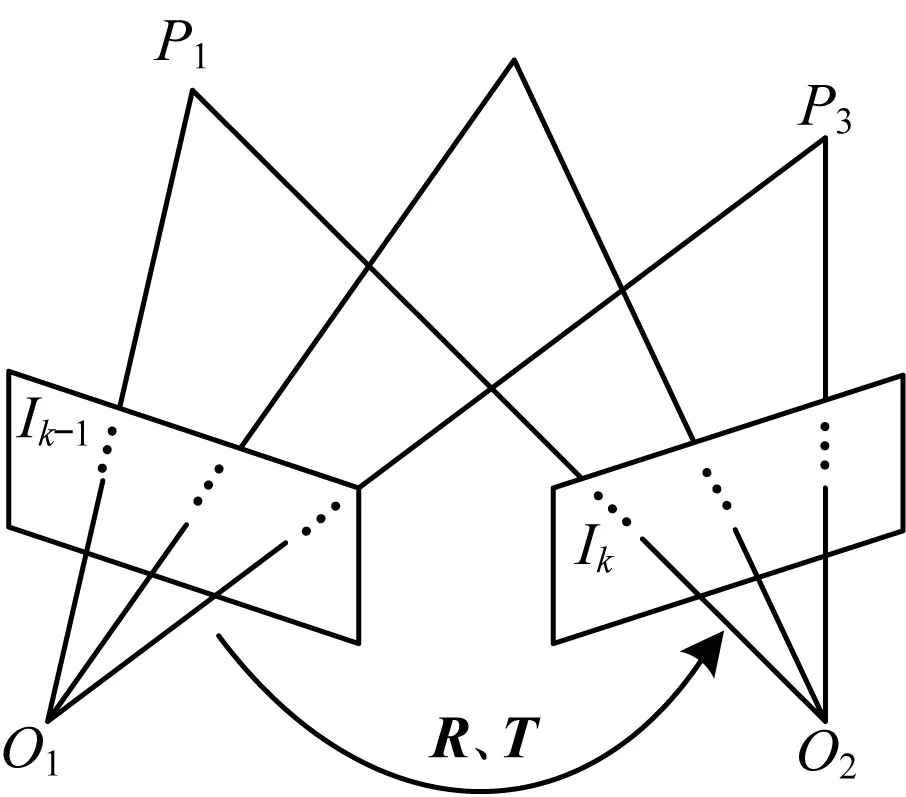
图4 帧间运动估计图

2.2 可变滑动窗口位姿优化

当新的关键帧到来时,会有一个可变滑动窗口形成,如图5所示。其中,路标点{P}是关键帧所观察到特征点对应的3D世界坐标点集,zk是路标点在第k个关键帧KFk上的投影坐标。滑动窗口内包含(m+1)个关键帧。窗口大小由当前帧所观察到的路标点决定,当前帧确定为关键帧后,会寻找和当前帧观察到相同路标点的关键帧,如果相同路标点的数量超过当前帧的一半,关键帧进入滑动窗口,滑动窗口大小加1。

图5 关键帧和非关键帧示意图

经过增量式运动估计后的关键帧KFk的初始位姿设为Xk,第i个路标点设为Pi,当在关键帧KFk上能够观测到Pi时,设观测到的像素坐标为zk,i,则可以用观测方程表示:

zk,i=h(Xk,Pi)+ek,i

(15)

因此,观测误差表示为:

ek,i=zk,i-h(Xk,Pi)

(16)

用x=[X1,X2,…,XN,P1,P2,…,PM]表示滑动窗口内的N个关键帧位姿和M个路标点3D坐标,则x是需要优化的变量。假设路标点{P}在N个关键帧里的投影坐标共有S个,即满足zk,i有值的(k,i)共有S对,那么局部位姿优化将通过调整Pi和Xk的值来使得所有的观测误差平方和最小,即最小化以下目标函数:

(17)

其中,Ωj为信息矩阵,是观测误差协方差矩阵的逆。

对式(17)采用高斯-牛顿[16]方法求解,对每一个误差项ej(x)和微小增量Δx,有:

(18)

将式(18)代入(17)式并作差ΔJ=J(x⊕Δx)-J(x),得到:

(19)

(20)

通过求解式(20)这个线性方程得到目标函数的梯度Δx,并对关键帧的位姿Xk和路标点坐标Pi进行更新:

x′=x⊕Δx

(21)

重复式(18)～式(21)直到优化变量x收敛,此时关键帧的位姿Xk和路标点Pi局部优化完成。非关键帧的全局位姿会随着关键帧的位姿局部优化而得到更新。

3 全局位姿优化

局部位姿优化能够减小双目视觉里程计的帧间运动估计的误差,随着相机的运动,帧间运动估计的误差会因为累积而变大,导致轨迹漂移。为了减小累积误差,本文采用了一种基于回环检测的全局位姿优化方法,一旦回环检测成功,将对回环内的所有关键帧位姿和路标点进行全局优化。

3.1 回环检测

回环检测需要在图像序列中找到出现在同一位置的关键帧,可以通过模式识别的方式来实现。本文采用词袋模型[18]进行回环检测。

词袋模型最早出现在信息检索领域中,忽略文本的语法与词序,用无序的单词表示文档。在计算机视觉中,图像类比于文档,图像块中的特征向量类比于单词,则图像的词袋模型可用图像中所有图像块的特征向量表示。本算法使用SiftGPU提取图像中的局部不变特征向量作为视觉词汇,并构建相应单词表,用单词表中的单词来表示每一个关键帧。具体步骤如下:

1)利用SiftGPU对大量的图像数据集进行特征提取和描述,获得作为视觉词汇的特征向量集。

2)利用K-means[19]聚类方法对特征向量集进行聚类,得到K个聚类中心,并且用聚类中心构造sift单词表。

3)对关键帧提取特征点和特征向量后,统计特征向量在单词表中出现的次数,将关键帧表示成关于sift单词表的K维向量。

对每一个关键帧会记录其Sift词袋模型向量,当新的关键帧到来时,通过计算词袋模型向量之间的距离来查询之前关键帧中相似的关键帧。将当前帧和相似度超过阈值的关键帧进行特征匹配和帧间运动估计,如果相似关键帧相对于当前关键帧具有微小的位移t和足够多的匹配点,且相似关键帧到当前关键帧之间初始位姿存在较大的位移,则判断回环成功。

3.2 全局优化窗口位姿优化

当前关键帧KFk与关键帧KFj回环检测成功,如图6所示。

图6 局部优化中的可滑动窗口示意图

(22)

同时在KFk处构造可变滑动窗口,利用2.2节的方法对当前关键帧KFk和滑动窗口内的关键帧KFj～KFj+m的位姿进行局部优化。

当可变滑动窗口中的关键帧局部位姿优化完毕,可变滑动窗口扩大至整个回环变成全局优化窗口,开始进行全局优化。全局优化的计算方法和式(17)～式(21)相同,不同的是在优化的过程中保持关键帧KFk和可变滑动窗口内的关键帧KFj～KFj+m的位姿不变,此时的优化变量变为x=[Xj+m+1,Xj+m+2,…,Xk-1,P1,P2,…,PM],目标函数变为:

(23)

全局优化完成对全局优化窗口内的所有关键帧位姿和路标点坐标的优化,同时更新非关键帧的位姿。经过全局优化后的移动机器人累积位姿误差得到显著消除,轨迹漂移减少。

至此,基于局部和全局优化的双目视觉里程计算法的流程如图7所示。

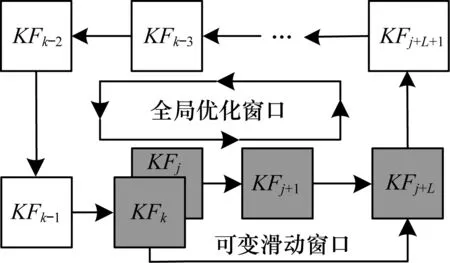
图7 全局优化示意图

4 实验与结果分析

4.1 实验数据与运行环境

本文实验所用电脑型号为MS-7885(CPU酷睿i7-5820k,主频3.30 GHz,内存16 GB),运行系统为Linux。测试数据选择计算机视觉算法测评平台KITTI[20]的双目图像数据集。该数据集是由搭载PointGray Flea2双目相机和OXTS RT3003 IMU/GPS导航系统的车辆在城镇街道行驶获取的,其中双目图像序列作为算法的输入,IMU/GPS的数据作为参考真实值评价算法的的精度。实验数据相关参数如表1和表2所示,实验环境的真实场景如图8所示。

表1 双目相机参数

表2 图像序列参数

图8 实验环境真实场景

4.2 算法性能分析与比较

4.2.1 算法性能分析

为清楚地看到局部优化和全局优化对位姿误差的消除效果,本文分别对算法在不做优化、只做局部优化、只做全局优化、局部和全局优化结合的定位效果进行了实验分析。图9是算法在4种情况下计算出的相机运动轨迹和实际参考运动轨迹的比较。可以看到,算法在不做优化时计算出的运动轨迹出现明显漂移,经过局部和全局优化后,运动轨迹和参考值基本重合。

图9 局部优化和全局优化对相机运动轨迹的影响

实验分别比较了不同的距离和速度下位姿误差,结果如图10所示。其中距离范围为50 m～800 m,每间隔50 m计算相应的旋转误差和平移误差,速度从6 m/s～16 m/s,每间隔2 m/s计算相应的旋转误差和平移误差,表3是相应的统计误差范围。

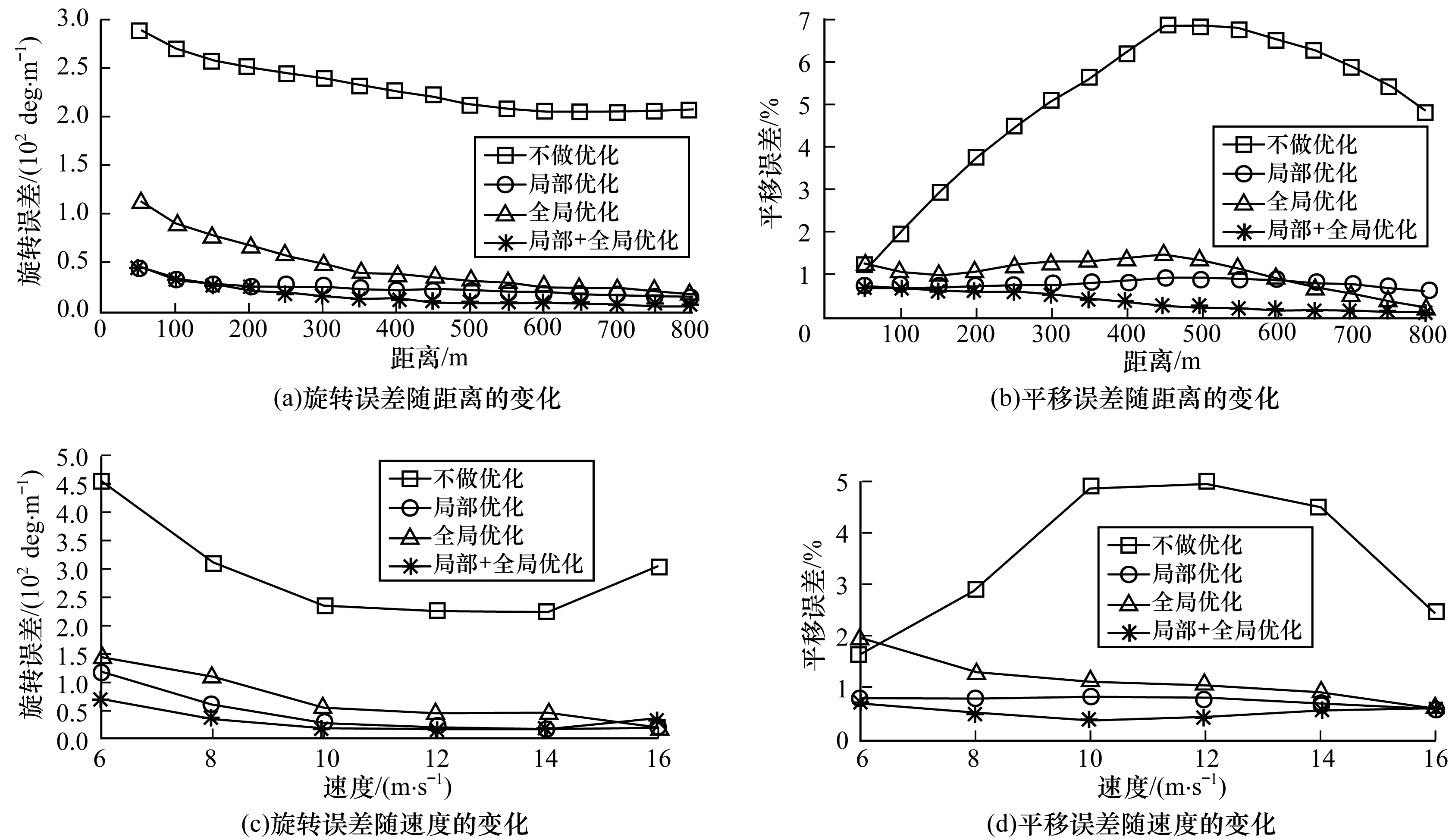
图10 局部优化和全局优化对位姿误差的影响

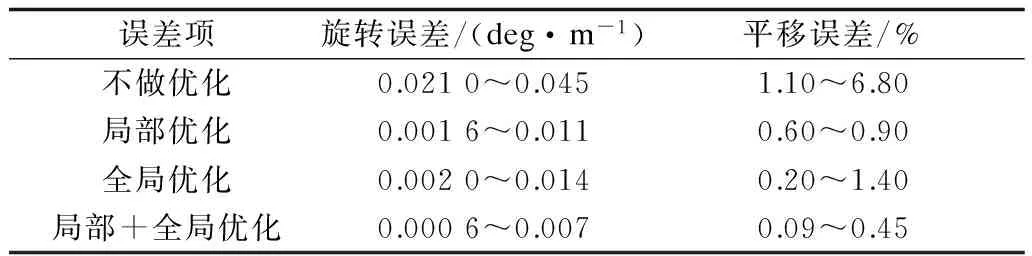
误差项旋转误差/(deg·m-1)平移误差/%不做优化0.0210～0.0451.10～6.80局部优化0.0016～0.0110.60～0.90全局优化0.0020～0.0140.20～1.40局部+全局优化0.0006～0.0070.09～0.45

可以看出,算法在不做优化时,旋转误差和平移误差较大。旋转误差最大达到0.045 deg/m,平移误差最大达到6.8%,同时图10(b)和图10(d)显示,随着运动距离和速度的增加,平移误差有逐渐增大的过程,这是算法在不做优化时位姿误差累积的结果。同时可以看到局部优化和全局优化分别能够单独减小位姿误差,而且局部优化对位姿误差的消除效果稍微要好于全局优化,这是因为局部优化始终在进行,而全局优化只有在回环检测成功的时候进行。

从图10(b)中可以看到,距离达到600 m时,全局优化的平移误差开始小于局部优化。这是由于此时场景中出现回环,全局优化开始进行,减小位姿误差的累积,定位更加精确。当局部优化和全局优化同时进行时,随着运动距离和速度的增加,旋转误差和平移误差基本保持最小并下降至趋于稳定,定位误差最小。

表4显示了本文算法的时间消耗。可以看出,基于局部优化和全局优化的双目视觉里程计没有显著增加每帧的处理时间,每帧耗时约90 ms,能够达到10 frame/s以上,基本满足实时性要求。

表4 平均每帧耗时比较 ms

4.2.2 算法性能比较

为了比较本文算法和其他双目视觉里程计算法精度,本文同时实验了Andreas Geiger等人开发的视觉里程计C++库libviso2[21]。libviso2是基于特征点匹配的双目视觉里程计,但其算法没有本文算法中的局部优化和全局优化。

图11是本文算法和libviso2算法分别在实验数据集运行后的平面轨迹图。可以明显看出,libviso2算法的运动轨迹在较长时间后开始偏离参考值,且偏移量越来越大。而本文算法运动轨迹基本和参考值保持一致,没有明显的偏移。

图11 本文算法和libviso2算法的相机运动轨迹图

图12是本文算法和libviso2算法计算出的位姿误差分析图,从中可以明显看出,本文的算法在不同速度和距离下旋转误差和平移误差都明显低于libviso2算法。libviso2算法的旋转误差最大达到0.018 deg/m,平移误差最大达到1.2%,而本文算法旋转误差最大为0.007 deg/m,平移误差最大为0.45%。从图12(b)中可以看到,随着距离的增加,libviso2算法的平移误差逐渐增加,而本文算法的平移误差逐渐减小,说明局部优化和全局优化能够显著减小帧间运动估计的误差和累积误差,定位更精确。

综上所述,本文算法在满足实时性要求的基础上,能够显著减小位姿误差,提高定位精度。

5 结束语

本文提出基于局部和全局优化的双目视觉里程计算法,设计了利用加速SIFT特征点匹配和RANSAC运动估计的双目视觉里程计。通过可变滑动窗口对位姿进行局部优化,减小帧间运动估计的误差,并采用回环检测对位姿进行全局优化减小误差累积。实验结果表明,本文算法在满足实时性要求的同时具有较高的定位精度。目前多传感器融合是移动机器人导航的趋势,因此,下一步将设计双目和惯性导航融合的视觉里程计,提高定位算法的鲁棒性和精度。

[1] SCARAMUZZA D,FRAUNDORFER F.Visual Odometry[J].IEEE Robotics & Automation Magazine,2011,18(4):80-92.

[2] MORAVEC H P.Obstacle Avoidance and Navigation in the Real World by a Seeing Robot Rover[M].Stanford,USA:Stanford University,1980.

[3] MATTHIES L,SHAFER S A.Error Modeling in Stereo Navigation[J].IEEE Journal of Robotics & Automation,1987,3(3):239-248.

[4] NISTER D,NARODITSKY O,BERGEN J.Visual Odometry[C]//Proceedings of 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:IEEE Press,2004:652-659.

[5] MAIMONE M,CHENG Y,MATTHIES L.Two Years of Visual Odometry on the Mars Exploration Rovers[J].Journal of Field Robotics,2007,24(3):169-186.

[7] ENGEL J,SCHÖPS T,CREMERS D.LSD-SLAM:Large-scale Direct Monocular SLAM[C]//Proceedings of European Conference on Computer Vision.Berlin,Germany:Springer,2014:834-849.

[8] DAVISON A J,REID I D,MOLTON N D,et al.MonoSLAM:Real-time Single Camera SLAM[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(6):1052-1067.

[9] MONTEMERLO M,THRUN S,KOLLER D,et al.FastSLAM:A Factored Solution to the Simultaneous Localization and Mapping Problem[C]//Proceedings of National Conference on Artificial Intelligence.New York,USA:ACM Press,2002:593-598.

[10] KLEIN G,MURRAY D.Parallel Tracking and Mapping for Small AR Workspaces[C]//Proceedings of the 6th IEEE and ACM International Symposium on Mixed and Augmented Reality.Washington D.C.,USA:IEEE Press,2007:225-234.

[11] 刘俸材,谢明红,王 伟.双目视觉的立体标定方法[J].计算机工程与设计,2011,32(4):1508-1512.

[12] LOWE D G.Distinctive Image Features from Scale-invariant Keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.

[13] WU Changchang.SiftGPU:A GPU Implementation of Scale Invariant Feature Transform(SIFT)[D].Chapel Hill,USA:University of North Carolina at Chapel Hill,2013.

[14] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

[15] RAGURAM R,CHUM O,POLLEFEYS M,et al.USAC:A Universal Framework for Random Sample Consensus[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(8):2022-2038.

[16] DENNIS J E,SCHNABEL R B.Numerical Methods for Unconstrained Optimization and Nonlinear Equations(Classics in Applied Mathematics,16)[M].[S.l.]:Prentice-Hall,1983.

[17] VARADARAJAN V S.Lie Groups,Lie Algebras,and Their Representations[M].Berlin,Germany:Springer,2013.

[19] AGARWAL S.Data Mining:Data Mining Concepts and Techniques[C]//Proceedings of International Conference on Machine Intelligence and Research Advancement.Washington D.C.,USA:IEEE Press,2013:203-207.

[20] GEIGER A,LENZ P,STILLER C,et al.Vision Meets Robotics:The KITTI Dataset[J].International Journal of Robotics Research,2013,32(11):1231-1237.

[21] GEIGER A,ZIEGLER J,STILLER C.StereoScan:Dense 3d Reconstruction in Real-time[C]//Proceedings of Intelligent Vehicles Symposium.Washington D.C.,USA:IEEE Press,2011:963-968.