足式机器人小腿减振控制研究

,, ,

(1.中国科学技术大学 信息科学技术学院,合肥 230027; 2.海军蚌埠士官学校 五系,安徽 蚌埠 233012)

0 概述

足式机器人在步行过程中,足部落地时因受到来自地面的冲击而造成整个身体的振动,且随着行走速度加快,冲击及振动将变得愈发剧烈。针对路面环境的位置情况,冲击及振动无法避免,因此,国内外足式机器人研究者通常选择在机器人脚底安装弹簧等弹性材料[1],缓和并衰减来自地面的冲击,但是这种方法引起了踝关节与地面之间的转动,不利于后续步态规划设计。文献[2]根据人类骨骼肌肉弹性变化的原理,采用力位混合控制,降低脚部落地时与地面的冲击力,该控制方法计算量大,难以满足实时控制要求。文献[3]提出通过调整运动脚和机器人上身平台的相对位置,避免由步距误差引起的撞击,但因关节间的运动误差及耦合干扰,相对位置计算难度大且碰撞不可避免。综合分析足式机器人行走稳定优化策略,目前的研究无法适应未知路面的变化,减振效果及应用前景不甚乐观。

近年来,主动减振控制在多种领域都得到比较成功的应用[4-5],其还对被动减振无法作用的低频以及超低频振动有较好的减振效果[6]。在传统的被动减振的基础上,引入主动减振控制,是本文提出的减小机器人上身平台振动的一种新的解决方法[7]。结合被动减振高频减振效果好、主动减振利于实现低频减振的特点,建立主被动联合减振能够发挥它们各自的优势,从而达到更好的减振效果。此外,主被动联合减振在作动器失效的情况下仍可以通过被动减振装置起到减振作用,其可靠性高于完全主动减振。

本文针对双足机器人行走过程中地面冲击对上身平台稳定性的影响,提出一种新的解决方案。首先在ADAMS中搭建足式机器人小腿主被动联合减振控制的虚拟样机。然后在Matlab中设计基于自抗扰控制的主动减振控制策略,将虚拟样机同控制模块进行交互式计算,实现主被动联合减振过程的虚拟仿真,优化机器人小腿样机整体性能。最后在系统平台上进行验证并进行数据分析。

1 减振小腿动力学建模

针对已有的小腿减振实验平台,在进行理论分析和控制算法设计之前,首先对平台进行机理建模。如图1所示为平台机理模型,被动部分采用弹簧-阻尼系统实现,来自地面的冲击经足部传递到上身平台,经被动减振衰减部分高频振动,主动减振作动器产生主动控制力与振动相互抵消,从而大幅减小振动。音圈电机作为主动部分作动器,位于上身平台和足部之间,用于产生主动控制力。

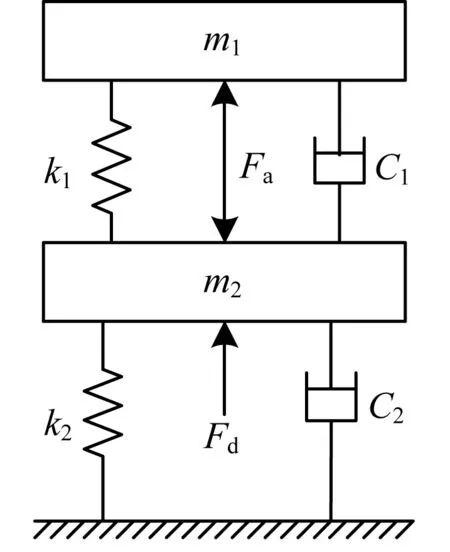
图1 主被动联合减振小腿机理模型

在图1中,m1为负载质量(包括主动部分和机器人上身平台),m2为机器人足部质量,ki、ci分别为系统的刚度和阻尼i=1,2,fd为地面激励信号,fa为主动控制力,x1、x2分别为m1、m2的垂直振动位移,以向上为正。

根据受力分析,可得到作用力关系如式(1)所示。

(1)

由式(1)可得负载加速度与激振力之间的传递函数为:

(2)

其中:

在一般情况下,根据系统机理可建立其数学模型,但在实际系统中存在诸多不确定性因素,如通道之间存在耦合、不同作用力的相互干扰等,导致数学模型不能完全体现机器人小腿主被动联合减振的动力学特性。ADAMS作为近年来在制造领域流行的虚拟样机技术,能够建立复杂机械系统的动力学模型和三维实体模型[8-9]。ADAMS集建模、计算和后处理于一体,已经得到广泛的使用[10]。基于ADAMS搭建的机械模型可弥补数学建模的不足,便于进行机械系统的单独分析或与Matlab进行控制策略的联合仿真研究。

基于ADAMS设计的虚拟样机模型如图2所示,主要有如下组成部分:支撑框架包括导柱、导套一体化支撑结构。上导套依靠内嵌滚珠移动,摩擦力较小,可忽略,下导套即底座,起固定作用;上身平台包括机器人小腿以上部分及音圈电机定子部分;足部包括机器人小腿以下部分及音圈电机动子部分。

图2 主被动联合减振小腿机械结构

对以上各模块之间添加运动副:底座添加固定副,使其固定于地面。内外8根导柱均固定于底座,保障弹簧在竖直方向运动。导柱与平台接触点添加滑移副、音圈电机定子和动子之间添加滑移副,使平台沿导柱运动。最后进行静平衡计算,得到系统各部分稳态时的受力平衡位置,并对各部分位置进一步调整以保证系统初始稳定性。

2 小腿减振控制系统设计

当机器人足部受到冲击时,最大限度减小冲击引起的振动,维持上身平台稳定性是足式机器人减振小腿稳定性控制的最终目的。针对稳定性问题,以上身平台振动加速度为控制目标,将实际加速度与目标加速度进行比较,将误差信号作用于自抗扰控制器并将加速度信息反馈给控制系统,建立闭环主动减振的控制策略。

自抗扰控制(ADRC)自从由韩京清先生于20世纪80年代提出以来[11],得到学者的广泛研究。ADRC在发挥传统PID控制优点的同时,不依赖于被控对象的精确模型,且抗干扰能力突出,具有较强的鲁棒性[12]。自抗扰控制器一般由跟踪微分器(TD)、扩张状态观测器(ESO)、非线性组合(NSEF)3个部分组成,如图3所示。TD为输入的信号安排过渡过程,以减少系统的超调;ESO依据输入到被控对象的输入量和被控对象的输出量来估计出系统的状态和扰动总和;NLSEF 即闭环系统的控制器。由于ADRC分为3个部分,因此需调节的参数较多,参数整定麻烦,工程上难以实现。文献[13]于2003年提出了一种更简单、易于实现的线性自抗扰控制(LADRC),将ADRC调参问题转化为带宽调参问题,从工程上解决了ADRC调参困难的问题。

图3 ADRC控制器结构

2.1 自抗扰控制器设计

控制器的目的是当机器人脚部受到冲击时,即上平台振动加速度改变,经过主被动联合控制振动加速度在极小范围内变化。在仿真过程中,取定振动加速度参考值为零,因此系统设计可以省略跟踪微分器的设置。采用二阶线性自抗扰控制算法设计减振小腿机械模型的控制器。

本文采用线性扩张状态观测器(LESO)为:

(3)

其中,a为上身平台实际振动加速度,b0为常数,z1为a的状态估计,z2为a的近似微分,z3为总和扰动的估计值,e为实际振动加速度及其状态估计之间的偏差,u为主动控制力,β01、β02和β03为可调参数,这里采用带宽来确定,取扩张状态观测器增益矢量:

(4)

其中,ω0需要根据系统带宽的要求确定或在线整定。

LADRC的控制量为:

(5)

此处u0的PI控制率为:

(6)

在上述算法中,a是机器人上身平台的输出量,u是控制输入,系统待调节参数为ω0、b0、kp和ki。

2.2 音圈电机控制模型设计

在主动减振技术中,作动器的选择和控制器设计是解决问题的关键。音圈电机作为一种新型电磁作动器,具有体积小、质量轻、响应快、高速度、高加速度等特点,广泛应用于精密仪器控制及振动主动控制中[14-15]。

音圈电机的工作基于安培力产生原理[16],电流在磁场中受到的磁场的作用力,如果导体长度l通过的电流I垂直于磁场,磁感应强度为B,则安培力F的大小为:

F=nBlI=KFI

(7)

其中,KF为音圈电机力常数。

由于ADAMS无法利用几何元素构建音圈电机电磁场,因此采用如下方式搭建音圈电机传递函数模型。如图4所示为音圈电机传递函数框图,A部分电压-输出力传递函数在Simulink中实现,B部分输出力-动子位移传递函数在ADAMS中实现。采用这种方式,建立的模型更加精确,贴近实际物理样机。

图4 音圈电机传递函数框图

根据基尔霍夫电压定律,音圈电机回路中的电压平衡方程为:

(8)

其中,UB=KBv为反电动势,v为音圈电机动子相对定子的运动速度,KB为反电动势常数。

变换式(8)得:

(9)

将式(7)、式(9)进行拉氏变换,消去中间变量I得音圈电机A部分的传递函数:

(10)

3 ADAMS与Matlab联合仿真实验

为验证本文设计的线性自抗扰控制算法的有效性,同时检测如图2所示减振小腿虚拟样机设计的合理性,本文进行ADAMS与Simulink的联合仿真实验。

3.1 激振信号的选取与仿真接口的设置

在减振设计中,通常把100 Hz以上的振动称作高频振动,6 Hz～100 Hz的振动定义为中频振动,6 Hz以下的振动为低频振动;另外,根据文献[17]在假人抗冲实验中的研究,小腿部位所受冲击约为脚部冲击的2倍。为了验证主动减振技术对低频振动抑制的有效性并检测足式机器人小腿机构的稳定性,本文选择1 Hz～10 Hz的半正弦信号,采取等幅变频率方式叠加产生混频信号作为激振信号。

通过ADAMS/Controls模块,建立ADAMS与Matlab之间数据交互的通道,生成Matlab选择窗口,建立联合仿真控制系统如图5所示。系统输入参数包括作用于音圈电机定子与动子之间的主动减振作用力和作用于足部的地面冲击,即激振信号。输出参数包括上身平台位移、速度、加速度和足部位移、速度、加速度。仿真时选择交互式计算,通信时间间隔为0.001 s。

图5 联合仿真控制系统框图

3.2 仿真实验与结果分析

考虑实际情况中机器人足部受到的激振,仿真中取激振信号最大幅值为50,如图6所示为激振信号的具体形式。设置仿真实验的总时长为50 s,仿真过程中前后8 s不施加主动控制,仅采取被动减振方式;中间30 s施加主动控制,采取主被动联合减振方式。改变减振方式2 s内不施加激振信号以避免前一种减振方式的效果对后一种减振方式造成干扰。系统各部分参数如表1所示,音圈电机相关参数如表2所示。

参数参数值m1/kg12.40m2/kg1.55k1/m13530.00k2/m7790.20c1/(m·s-1)81.90c2/(m·s-1)65.90

表2 音圈电机参数

主动控制算法ADRC控制器参数选取如下:ω0=15,b0=650,kp=1,ki=10 500。

图7和图8分别为2种减振方式下足部振动加速度曲线和上平台振动加速度曲线。相比于图7足部振动加速度曲线,在0 s～8 s时间内,图8中单纯被动减振方式对上身平台的振动起到了一定的抑制作用,但是系统仍存在较大的振动;在10 s～40 s加入主动减振控制力以后,上身平台的振动大幅衰减;在42 s～50 s时间内,当系统失去主动控制力以后,减振效果也随之变差。仿真实验结果一方面验证了被动减振对低频率的振动抑制效果不明显,另一方面可以看出主动减振有效抑制了低频振动,达到了针对中低频段振动衰减的目的。图9为主被动联合减振方式下主动控制力的变化曲线。

图7 2种减振方式下足部加速度曲线

图8 2种减振方式下上身平台加速度曲线

图9 主动控制力变化曲线

为了定量分析主被动联合减振方案的减振效果,表3给出了在机器人小腿部位受到不同幅值激振信号时,2种减振方式下机器人上身平台稳态时的最大振动加速度数值以及相应的主动控制力峰值。从实验结果可以看出,在不同激振信号的作用下加入主动控制力后,相比于单纯的被动减振效果提高了约3个数量级,主被动联合减振相对于单纯的被动减振具有较大的优势。

表3 主被动/被动减振效果对比

3.3 实验验证

基于理论推导及仿真分析进行实验验证,平台实物如图10所示,传感器安装在上平台顶部,相应的控制模块及电机驱动器如图11所示。在CCS6.0软件开发平台上进行相关模块控制及线性自抗扰控制算法的编写,采用平台的自由落体方式进行实验,激振信号来自落地瞬间地面的反作用力。

图10 减振平台实物图

图11 控制模块及电机驱动器

在实验过程中,模数转换模块每秒采样100个数据,实验结果如图12所示,图12(a)为被动减振情况下上身平台加速度变化曲线,系统最大振动加速度约为4 m/s2,系统大约2 s后达到稳定状态;图12(b)为加入主动减振控制算法后的上身平台加速度变化曲线,系统整体振动加速度相比于被动减振被明显抑制,同时系统大约在1 s后稳定,实现了振动时间的优化。

4 结束语

针对足式机器人行走过程中的冲击振动问题,本文提出一种以音圈电机为作动器的主被动联合减振控制策略。首先在ADAMS中搭建足式机器人小腿主被动联合减振控制的虚拟样机。然后在Matlab中设计基于自抗扰控制的主动减振控制策略。最后在系统平台上进行验证并进行数据分析。实验结果表明,基于音圈电机的主被动联合减振效果明显,证实了主被动联合减振方法相对于传统被动减振的优越性,以及使用音圈电机作为主动减振作动器的可行性,机器人上身平台减振效果较好。在实际实验平台上进行减振控制研究过程中发现,数模转换模块采样频率过高,导致电机反应不及时,无法准确改变电机的运行,实际减振效果与仿真还有一定的偏差,下一步将对模型中的不确定情况进行研究。

[1] YI K Y.Locomotion of a Biped Robot with Compliant Ankle Joints[C]//Proceedings of IEEE International Conference on Robotics and Automation.Washington D.C.,USA:IEEE Press,1997:199-204.

[2] SILVA F M,TENREIRO M J A.Position/Force Control of Biped Walking Robots[C]//Proceedings of IEEE International Conference on Systems,Man,and Cybernetics.Washington D.C.,USA:IEEE Press,2000:3288-3293.

[3] TAKANISHI A,ISHIDA M,YAMAZAKI Y,et al.Realization of Dynamic Walking by the Biped Walking Robot[J].Journal of the Robotics Society of Japan,1985,3(4):325-336.

[4] LU Zhenli.Design of a 3DOF Passive Rotating Platform for the Adaptive Motion Planning of a Single-legged Robot[C]//Proceedings of IEEE International Conference on Autonomous Robot Systems.Lisbon,Portugal:IEEE Press,2013:1-6.

[5] MITSUHASHI K,BIWA T,MIZUHARA S.Application of Active Vibration Isolating System to Diesel Engine Mounting[C]//Proceedings of CIMAC’00.Washington D.C.,USA:IEEE Press,2000:139-148.

[6] HOQUE M E,MIZUNO T,ISHINO Y,et al.A Three-axis Vibration Isolation System Using Modified Zero-power Controller with Parallel Mechanism Technique[J].Mechatronics,2011,21(6):1055-1062.

[7] 毛伟伟,周 烽,梁 青,等.基于自抗扰控制的机器人小腿减振研究[J].计算机工程,2016,42(7):293-298.

[8] 周晓光,黄景涛.Adams与Simulink的分布式协同仿真[J].计算机工程,2011,37(15):228-231.

[9] 韩 虎,曾庆良,孙成通,等.复杂产品虚拟样机协同开发平台设计与实现[J].计算机工程,2009,35(1):260-262.

[10] 李曾刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2007.

[11] 韩京清.自抗扰控制技术:估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008.

[12] 夏露露,许化龙,夏 昕.惯性平台调平回路的自抗扰控制[J].电子测量技术,2010,33(4):106-108.

[13] GAO Z.Active Disturbance Rejection Control:A Paradigm Shift in Feedback Control System Design[C]//Proceedings of 2006 American Control Conference.Washington D.C.,USA:IEEE Press,2006:14-16.

[14] 盖玉先,董 申.振动主动控制中的作动器技术[J].航天工艺,1999,12(6):45-48.

[15] MACLEAN B J,DRAOER J L,MISRA M S.Development of a Shape Memory Material Actuator for Adaptive Truss Applications[J].Journal of Intelligent Material Systems and Structures,1991,2(3):261-280.

[16] 陈照波,吕俊超,焦映厚.音圈电机驱动的双层主动隔振系统设计与仿真[J].噪声与振动控制,2012,32(5):26-30.

[17] 黄建松,汪 玉,李政年,等.舰员抗冲击鞋性能试验及评估方法研究[J].中国生物医学工程学报,2012,31(3):466-470.