斜拉桥损伤可识别性传感器的优化布置方法

刘 杰， 王海龙， 张志国， 张瑞云， 曹立辉， 王国安

(1.石家庄铁道大学土木工程学院，河北石家庄050043;2.西南交通大学土木工程学院，四川成都610031;3.石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室，河北石家庄050043;4.河北建筑工程学院土木工程学院，河北张家口075000)

传感器系统［1］是桥梁结构健康监测系统的重要组成部分.根据传感器系统采集的振动数据进行环境激励下的模态参数识别［2］，所获得的模态参数(包括频率和测点振型值)是进行动力损伤识别［3］的基础.

斜拉桥跨度大、体型巨大、型式复杂，加上现场条件和健康监测系统建造、维护费用的限制以及海量数据处理的困难，只能布置有限数量的传感器.将有限的传感器布置在斜拉桥上，是否能准确识别出斜拉桥的模态参数(简称模态可观测性)以及准确识别模态参数是否对结构损伤足够敏感(简称损伤可识别性)，是需要考虑的两大问题，也是关系损伤识别有效性的关键因素［4］.因此，传感器优化布置(类型、数量和位置)［5］的研究具有十分重要的意义.

近二三十年来，基于振动模态测试的传感器优化布置研究逐渐受到重视，并且取得了许多重要的研究进展，可归纳为［4］:第1类，基于模态可观测性的传感器优化布置方法，该类方法可观测的模态应具有一定的准确性和线性无关性，包括有效独立法(EI法)、Guyan模型缩减法、奇异值分解法、模态保证标准法(MAC法)、基于模态运动能法、智能算法优化法［6］、混合法等;第2类，基于损伤可识别性的传感器优化布置方法，该类方法是指获取的模态参数对结构的局部损伤和状态退化足够敏感，包括基于损伤灵敏度分析法和基于易损性分析布设法［7］等.

第1类中，各种方法存在相互不能满足要求、优化陷入局部最优、优化效率低等缺陷［8］，且无法考虑模态参数对局部损伤的敏感性情况以及反映传感器位置对结构损伤识别的影响，也即不满足损伤可识别性的要求.

第2类中，损伤灵敏度法需要对结构损伤灵敏度Fisher信息矩阵求逆，而Fisher阵的逆矩阵不一定存在，为避免对损伤灵敏度Fisher信息矩阵求逆，采取分解每个自由度对Fisher信息阵迹的贡献来选择最佳测点，该方法获得测点模态满足不了模态可观测性的要求，即测点模态测不出［4］;基于易损性分析布设法由于对损伤部位及失效路径的预测与复杂的实际情况难免出现偏差等局限性.

当前传感器优化布置研究大多分别基于两类方法单独进行优化方法，存在优化易陷入局部最优、优化效率低等缺陷，而且满足模态可观测性并不一定满足损伤可识别性［9］.而对于以损伤识别为目的的健康监测系统，传感器优化布置的损伤可识别性特别重要.

本文从传感器优化布置的损伤可识别性要求出发，利用参数试验法和参数相关性理论，提出并得到一种包含所有梁段损伤信息的节点自由度损伤信息指标，该指标通过计算所有梁段单元的损伤因子与节点自由度振型值之间的相关性而获得.对该指标排序可获得节点自由度包含损伤信息多少的次序，即每个自由度的损伤敏感性排名.此过程无需优化迭代.该方法可避免对结构进行大范围的优化计算，可避免优化陷入局部最优、优化效率低等缺陷.

1 节点自由度损伤信息指标法

根据文献［10］，本文采用节点自由度振型值、曲率值等任意动力指纹节点自由度损伤信息指标法，其核心思想是:利用节点自由度振型响应(或曲率等)与单元损伤因子(可指损伤率)的之间相关性，可反映损伤因子对自由度振型值影响程度的性质，利用相关性构造出一种全新的指标，新指标可以实现传感器优化布置的损伤可识别性的目标.损伤因子是指改变单元的弹性模量或截面特性用来模拟损伤情况，即仿真试验中改变的输入设计参数.

有限元模拟不但适用于梁单元，也适用于实体单元，不因响应类型或单元类型变化而影响其使用.新指标中所指自由度的数目与所提取的响应方向有关，可提取节点的所有位移自由度，也可仅提取感兴趣或可提取的有限个位移自由度.

确定新指标时，根据试验方法不同，设定单元的损伤因子，利用有限元软件计算节点自由度的振型响应(或曲率等)，获得节点自由度振型响应(或曲率等)与单元损伤因子之间的相关性指标，对指标排序可获得节点自由度包含损伤信息多少的次序，即每个自由度的损伤敏感性排名.

本文利用参数试验法［11］进行参数的显著性检验，研究所有梁段单元的损伤因子对节点自由度振型值的影响.参数显著性检验具有全局性，克服了敏感性分析的缺陷［12］.参数试验法是指在其它因子都保持在基值的情况下，使每个因子独立的变化所有指定水平进行研究，确定每一个设计因子独立于其它所有因子情况下对响应的敏感性，可在多个水平上研究多个因子，只需对较少的设计点进行评估.参数试验需要进行Ansys有限元仿真分析，其分析次数为

式中:m为因子个数;

li为第i个因子的水平数.

式(1)中，因子是指试验中改变的输入设计参数，是造成试验指标按某种规律发生变化的那些原因，如引起结构损伤的材料弹性模量、尺寸或质量的改变等;水平是指因子的不同状态，即输入设计参数的数值，如材料弹性模量的改变量(或改变率)等.计算时可根据分析内容结合计算效率有针对性的选择因子、因子个数及因子的水平.

参数之间的相关性分析是参数显著性检验的重要方法之一［13］，本文根据参数的相关性分析构造了可反映结构损伤信息程度的指标，构造指标的过程主要包括计算参数间相关性与求和.

(1)计算参数间的相关性

为了全面评估主梁所有梁段单元的损伤对节点自由度振型值的影响情况，需要计算所有输入参数对某个输出参数的相关性.参数间的相关性rXY计算见式(2).

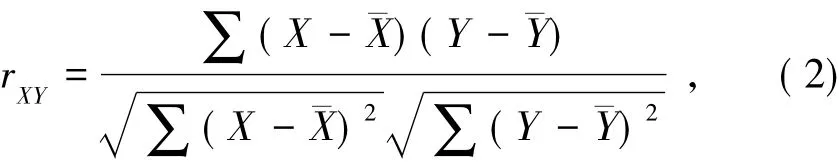
式中:X、Y为任意两参数参数;

珔X、珔Y为参数的统计平均值;

rXY分别对应正相关和负相关，介于－1到1之间，其绝对值越接近1，两参数关联程度越强，其绝对值越接近0，两参数关联程度越弱.

(2)求和获得节点自由度的损伤信息指标

取损伤因子对应参数X，节点自由度振型值对应参数Y，两参数相关性越大，说明损伤因子与节点自由度振型值相互关联越密切，损伤因子对自由度振型值的影响越大;反之，该自由度振型值所包含的结构损伤信息就越多.正相关与负相关所反映的信息程度意义上是一样的.

为了衡量哪阶振型哪个节点自由度所包含的损伤信息程度，构造包含损伤信息指标为

式中:Djk为第 j阶模态第 k自由度的损伤信息指标;

Xi为第i个损伤因子;

d为损伤因子的个数;

Yjk为第j阶模态k自由度的振型响应.

Djk可反映参数Yjk包含的损伤信息量的大小程度，该值越大表示第j阶模态第k测点自由度的振型值所包含的损伤信息就越大，就越能显著的识别结构的损伤情况.

对于利用多阶模态情况，构造指标为

式中:n为所考察的模态阶数.

对所有节点自由位置上的该指标进行排序，具体应用时，根据所需要的自由度数目以及模态阶数计算相应的Dk指标进行排序，可获得节点自由度损伤信息指标序列{Dk}，其中，k∈［1，n］区间中的某种组合，n为节点自由度总数，取关注的前几阶模态的前几个测点自由度.

本文将该指标命名为节点自由损伤信息指标，如拟监测的模态阶数为5阶，节点自由度总数为85，监测41个梁段损伤情况，则第3个节点自由度的损伤信息指标为

求出所有节点自由的损伤信息指标排序，获得满意布点数的测点位置序列.

2 传感器优化布置第1类方法

根据节点自由度损伤信息指标法确定每个自由度的损伤敏感性排名后，根据满意的传感器数量，依次序提取自由度位置.设满意的传感器自由度数为10个，可提取前20个自由度位置，然后按照传感器优化布置第1类方法进行再计算，确定最终的传感器优化布置方案.利用Matlab软件编制了改进的有效独立法(EI，effective independence)［14］、模态保证标准法(MAC，modal assurance criterion)、和遗传算法(GA 法)［6，15-18］进行分析.

3 斜拉桥传感器优化布置及检验

斜拉桥及创建基准有限元模型的方法同文献［19］，斜拉桥结构模型如图1所示.

为了与振型实测情况吻合，动力分析时，采用主梁测点最大元素归一化方法提取竖向位移振型，提取前5阶模态，基准有限元模型与采用环境激励测得的成桥竖向频率如表1所示.

由表1可知，基准有限元模型与实测频率较为吻合，最大误差为1.4%，表明本文创建的基准有限元模型是可行的，基于基准有限元模型的后续动力分析及损伤识别是有效的.

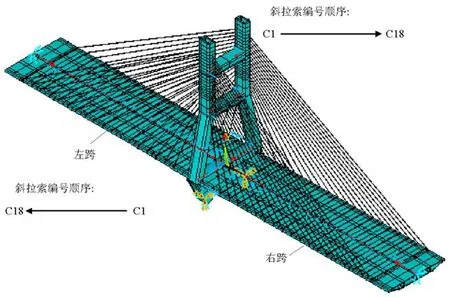
图1 斜拉桥结构模型Fig.1 Structural model of the cable-stayed bridge

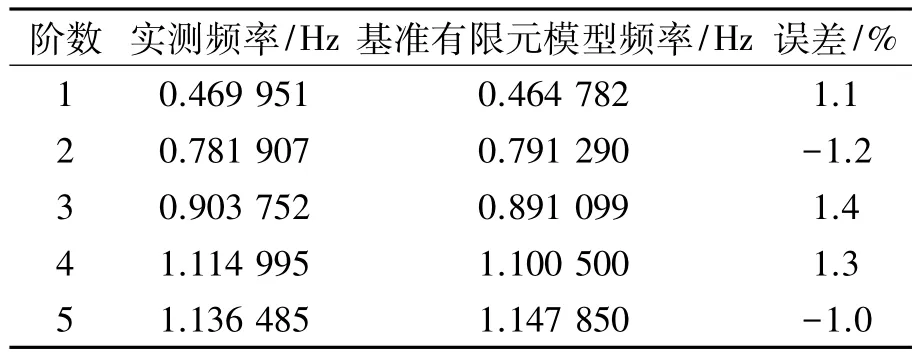
表1 基准有限元模型与实测频率对比Tab.1 Comparison between calculated and measured frequencies

将全梁共85个节点的前5阶归一化振型值作为响应.采用全梁所有梁段的单元弹性模量改变率共计41个损伤因子.为识别健康监测最有意义的早期损伤，损伤因子取 0.00、0.01 和 0.02 各 3 个水平.采用参数试验法进行试验设计，由式(1)计算可知，共有124次仿真试验，设计矩阵如表2所示，限于篇幅，仅提供前10次和后10次部分因子的仿真试验设计矩阵数据.

表2中，D10_1z(y)表示左(右)跨10#块单元对应的弹性模量改变率.通过表2的设计矩阵进行Ansys仿真试验，求取前5阶归一化振型数据如表3所示，限于篇幅，仅提供部分节点(6个节点)的前10次和后10次部分因子的仿真试验设计矩阵数据.

表3中，n1_13为第1阶第13个节点(主梁按大小排序的第13个节点)的归一化竖向位移振型值.

由式(2)计算所有损伤因子与所有主梁节点各阶模态振型值之间的相关系数;由式(3)计算各节点对应的总绝对相关度，此值综合反映主梁损伤程度，是损伤可识别性较灵敏的参数.根据选取的模态阶数;由式(4)计算对应节点位置的节点自由度损伤信息指标并排序，根据满意的传感器布点数，从大到小依次选取.

模态阶数为3～5，满意的传感器布点数为20个时，对应的布点位置如表4和图2所示.特别说明，Ansys建模时未对主梁节点进行排序，为描述清晰起见，将主梁对应的节点编号转化为从1开始自左至右编号，共计85个节点.

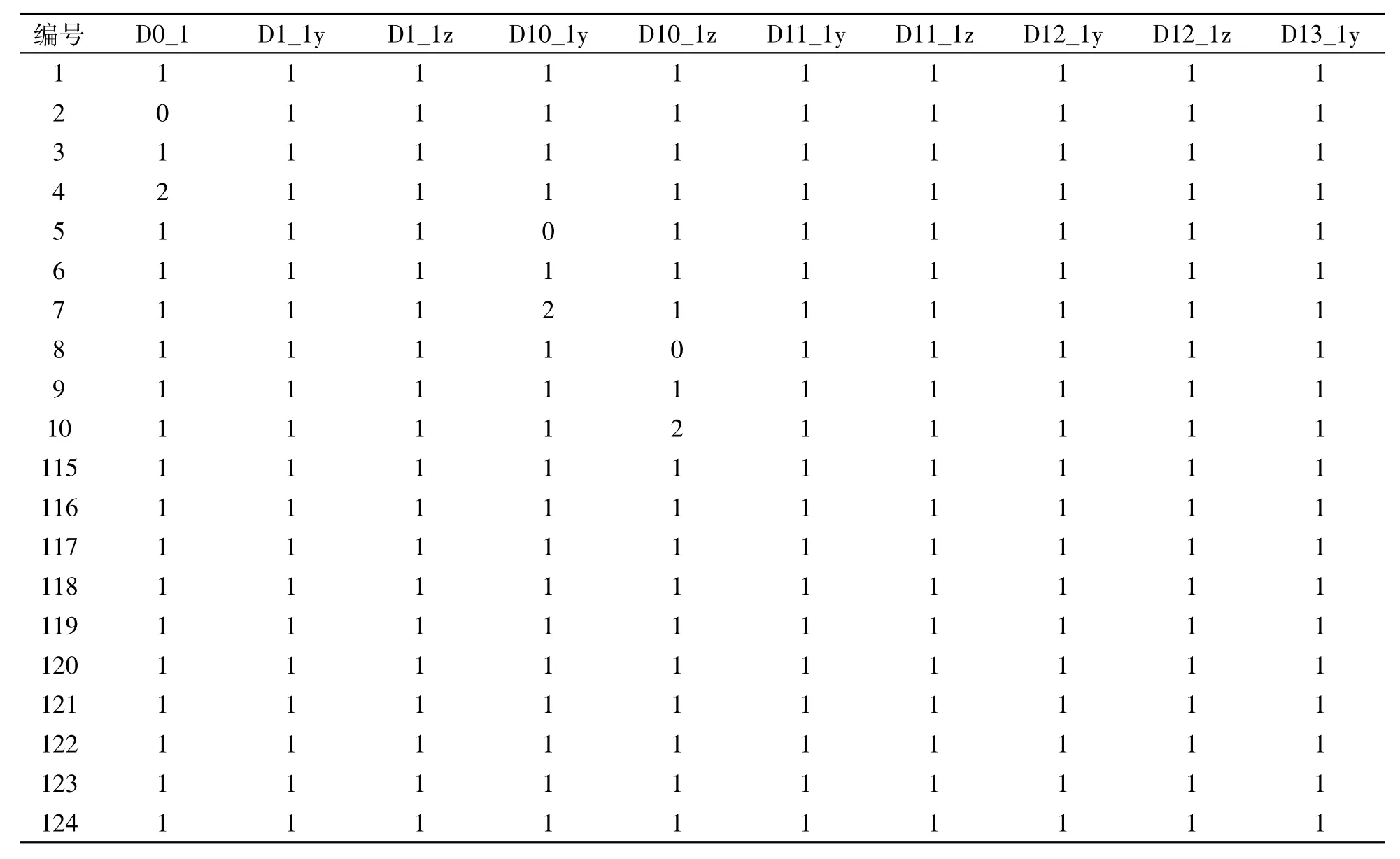
表2 提取不同模态数时较大的损伤信息指标及对应节点Tab.2 Partial data of the design matrix obtained using the parameter study method

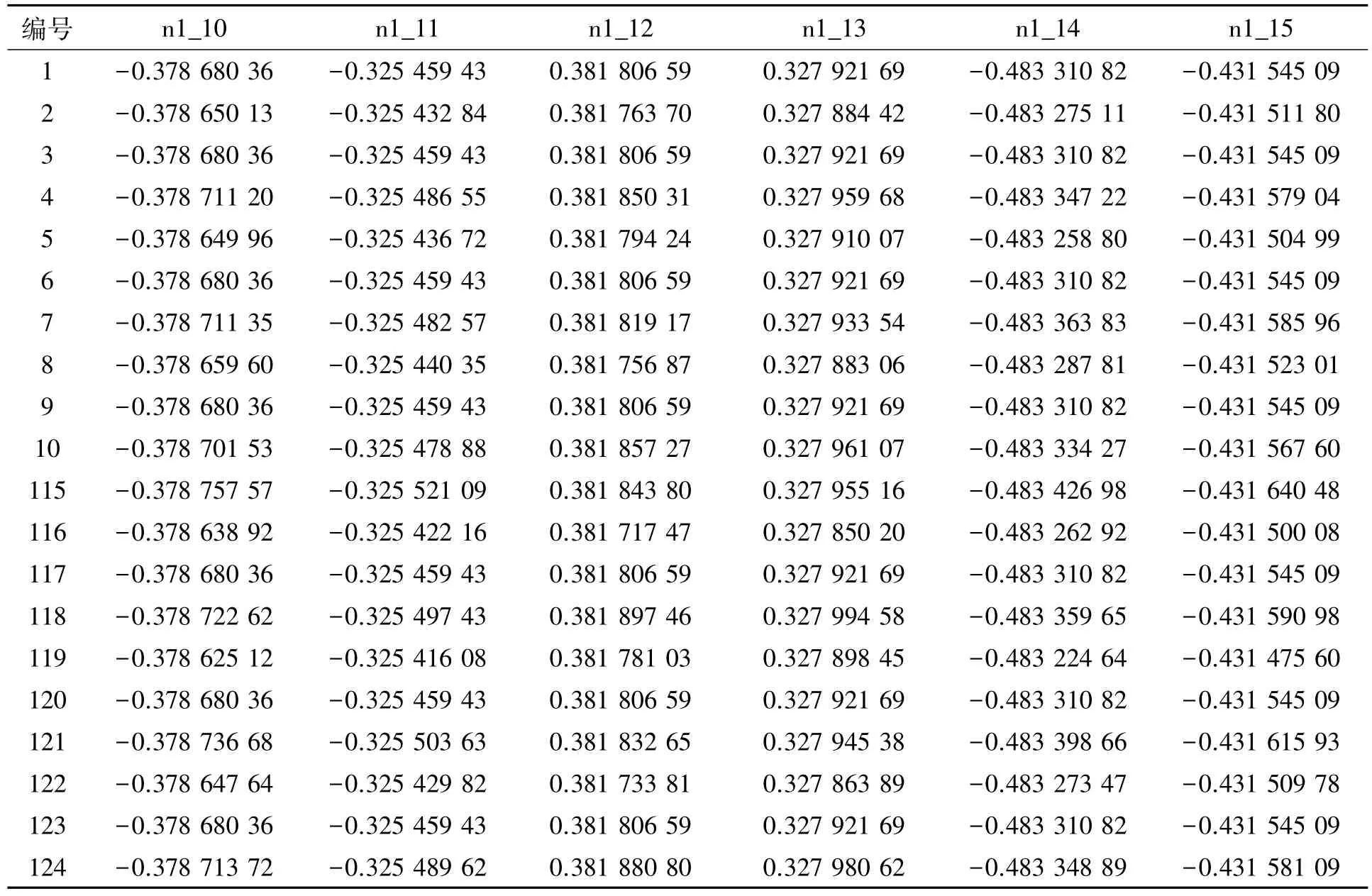
表3 仿真试验部分节点的前5阶归一化振型值Tab.3 Normalized mode shape values of the first five orders of the partial nodes obtained via simulation m

表4 不同模态阶数时传感器布点位置Tab.4 Sensor locations for different mode shape orders

由图2可知，提取的模态阶数不同时，选取的20个节点不同，提取的振型数目会影响节点包含的损伤信息.提取的振型数目越大，相同测点数目情况下，所包含的结构损伤信息越大.

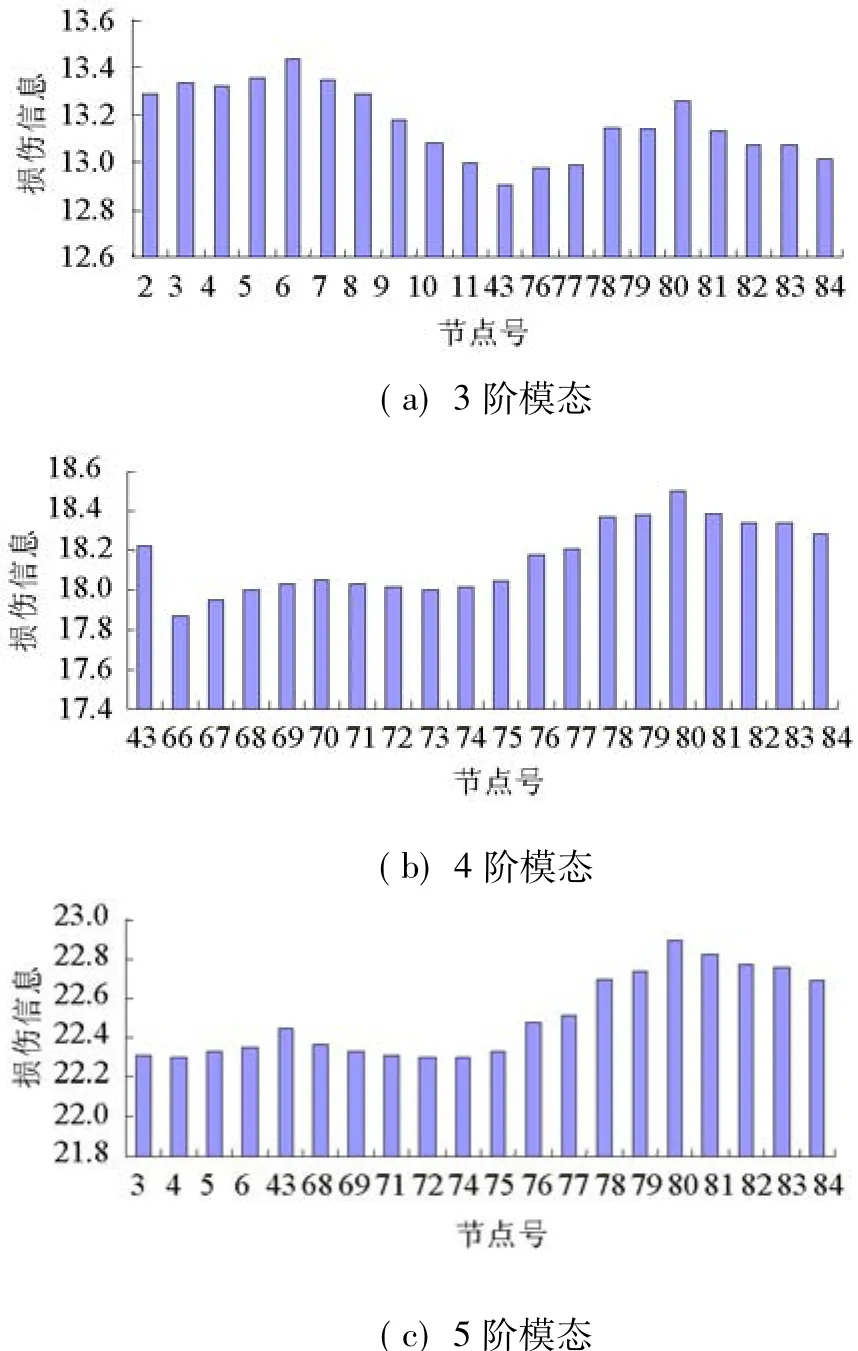
图2 提取模态数不同时的节点及其损伤信息指标Fig.2 High damage information index and its nodes with different modal orders

对应的MAC法矩阵值如图3所示.由图3可见，满足损伤可识别性的前提下，部分MAC法矩阵非对角线元素比较大，说明存在夹角比较小的振型向量，该值保证了模态可观测性，是在本文指标法排序筛选的基础上对传统MAC法的优化.特别说明，MAC法本身与损伤并没有直接关系，但经过本文方法基础上再进行MAC法的优化，使得所获得的传感器布置方案不但具有损伤可识别性而且满足模态可观测性.

图3 不同的模态时的MAC值Fig.3 MAC values for d ifferent modal order numbers

由表5可见，考虑的模态阶数不同，布置位置有别.模态阶数越高，节点损伤信息指标所包含的信息越多.但随着所要求识别的模态阶数的提高，对健康监测系统软硬件的要求越高.目前的模态参数识别水平下，对于低阶模态的模态参数更易精确识别.实桥应用时可综合考虑这些矛盾因素选择模态阶数.

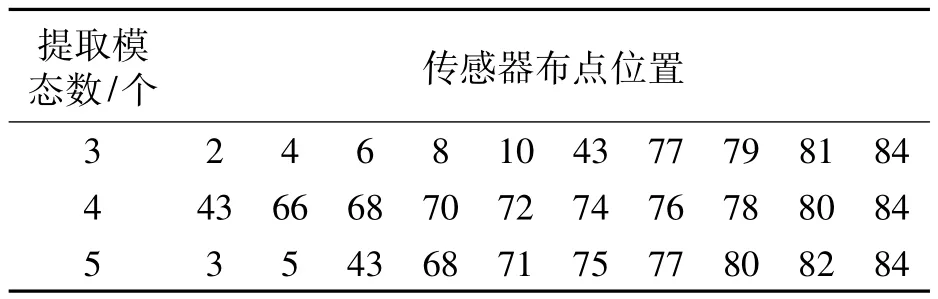
表5 最终的传感器布点位置Tab.5 Final sensor locations

在此基础上进行EI法和GA法分析，排除无法识别的测点后，获得传感器优化布置结果一致，如表5所示，相应测点E矩阵值如图4所示，MAC值如图5所示.

图4 不同模态阶数时E值(进一步分析后)Fig.4 E values for different modal order numbers(after further analysis)

由图4可见，所得测点最大程度的保持了相应模态向量间的线性独立性.

由表5可见，模态阶数不同时，传感器布置位置有较大差别，究其原因是在构造指标Dk时取绝对值之故，使得指标Dk损伤可识别性较灵敏.此原因也导致了当模态阶数为 3时，布点 2、4、6、8、10比较集中等问题.实桥应用时，可适当删减或采用选择主梁对称的另一端节点等方式进行处理即可.

由图5可见，非对角线元素非常小，远低于0.25，基本达到0的优良标准，保证了所监测振型的正交性，模态可分辨程度非常高.说明先由节点自由损伤信息指标排序，再经由EI法、MAC法和GA法等传感器优化布置第一类方法处理，非常容易得出满足要求的一致的加速度优化布置方案.

图5 不同模态阶数时MAC值(进一步分析后)Fig.5 MAC values for different modal order numbers(after further analysis)

为进一步论证论文所提方法的正确性和优越性，单独采用有效独立法(EI法)进行传感器优化布置.模态阶数分别是 3、4、5时，满意的布点数10个时优化布置传感器结果如表6所示.

表6 EI法的传感器布点位置Tab.6 Sensor locations using the EI method

经过验证优化测点无法保证模态正交性，且与本文所提出的方法相比，自由度损伤信息指标总和:3阶时高出589;4阶时高出582;5阶时高出591.EI法优化测点所包含的损伤信息量少，较难灵敏识别结构的损伤情况.

4 结论

(1)基于损伤可识别性的要求，提出并实现了一种传感器优化布置方法，将该方法命名为节点自由度损伤信息指标法.该方法无需优化，可避免优化陷入局部最优、优化效率低等缺陷.该方法在国内外该领域的提出尚属首次，且经过理论与仿真分析，证明了可行性和有效性.

(2)本文提出的节点自由度损伤信息指标法属于传感器优化布置的第2类方法，这种方法在满足损伤可识别性的前提下，结合第1类方法，可以快速得到既满足损伤可识别性又满足模态可观测性的传感器优化布置方案.

(3)本文从解决斜拉桥主梁损伤可识别性角度出发，进行了传感器优化布置方法的研究，若是斜拉索损伤、支座或者边界伸缩缝损伤的可识别性问题，只需在利用本文所提出的节点自由度损伤信息指标法时采用相应的损伤因子和响应即可.

［1］ 张明金，李永乐，余显全，等.桥塔上风传感器安装位置对测量结果的影响［J］.西南交通大学学报，2015，50(4):617-662.ZHANG Mingjin，LI Yongle，YU Xianquan，et al.Influence of wind sensor location on bridge tower on measurement result［J］.Journal of Southwest Jiaotong University，2015，50(4):617-662.

［2］ 蒲黔辉，秦世强，施洲，等.环境激励下钢筋混凝土拱桥模态参数识别［J］.西南交通大学学报，2012，47(4):539-545.PU Qianhui，QIN Shiqiang，SHI Zhou，et al.Modal parameter identification ofreinforced concrete arch bridge under ambient excitation［J］. Journal of Southwest Jiaotong University，2012，47(4):539-545.

［3］ 吴向男，徐岳，梁鹏，等.桥梁结构损伤识别研究现状与展望［J］.长安大学学报:自然科学版，2013，33(6):49-58.WU Xiangnan，XU Yue，LIANG Peng，et al.Research status and prospect of bridge structure damage identification［J］. Journal of Chang'an University:Natural Science Edition，2013，33(6):49-58.

［4］ 孙小猛，冯新，周晶.基于损伤可识别性的传感器优化布置方法［J］.大连理工大学学报，2010，50(2):264-270.SUN Xiaomeng，FENG Xin，ZHOU Jing.A method for optimum sensor placement based on damage identifiability［J］. JournalofDalian University of Technology，2010，50(2):264-270.

［5］ 刘国华，吴志根.引入信息熵理论的砼结构损伤动力识别新思路［J］.振动与冲击，2011，30(6):162-171.LIU Guohua，WU Zhigen.New thought on dynamic identification technology for damage detection of RC structures by introducing information entropytheory［J］.Journal of Vibration and Shock， 2011， 30(6):162-171.

［6］ 单德山，王振华，李乔.大跨度铁路钢桁斜拉桥传感器优化布置［J］.土木建筑与环境工程，2011，33(增刊 1):156-160.SHAN Deshan，WANG Zhenhua，LI Qiao.Optimal sensors placement for long-span railway steel truss cable-stayed bridge［J］.Journal of Civil，Architectural＆ Environmental Engineering，2011，33(S1):156-160.

［7］ 杨伟，孙利民.针对结构易损场景监测的传感器优化布置方法［J］.同济大学学报:自然科学版，2015，43(11):1670-1676.YANG Wei，SUN Limin.Optimal sensor placement for monitoring structural vulnerable scenarios［J］.Journal of Tongji University:Natural Science，2015，43(11):1670-1676.

［8］ 伊廷华，张旭东，李宏男.基于分布式猴群算法的传感器优化布置方法研究［J］.工程力学，2014，31(3):93-100.YIN Tinghua， ZHANG Xudong， Li Hongnan.Distributed monkey algorithm for optimal sensor placement［J］.Engineering Mechanics，2014，31(3):93-100.

［9］ 赵建华，张陵，孙清.利用粒子群算法的传感器优化布置及结构损伤识别研究［J］.西安交通大学学报，2015，49(1):79-85.ZHAO Jianhua，ZHANG Ling，SUN Qing.Optimal placement of sensors for structural damage identification using improved particle swarm optimization［J］.Journal of Xi'an Jiaotong University，2015，49(1):79-85.

［10］ 相阳，罗永峰，廖冰，等.球面网壳地震动输入与振型响应的相关性［J］.浙江大学学报:工学版，2016，50(6):1040-1047.XIANG Yang，LUO Yongfeng，LIAO Bing，et al.Correlation between seismic input and modal response of spherical latticed shell［J］.Journal of Zhejiang University:Engineering Science，2016，50(6):1040-1047.

［11］ 刘江南，洪义海.三轴数控平面磨床几何精度分析与稳健设计［J］.湖南大学学报:自然科学版，2016，43(4):1-8.LIU Jiangnan，HONG Yiha.Analysis and robust design of geometric accuracy of a three-axis CNC surface grinding machine［J］.Journal of Hunan University:Natural Sciences，2016，43(4):1-8.

［12］ 单德山，孙松松，黄珍，等.基于试验数据的吊拉组合模型桥梁有限元模型修正［J］.土木工程学报，2014，47(10):88-95.SHAN Deshan，SUN Songsong，HUANG Zhen，et al.Finite element model updating of combined cablestayed suspension model bridge based on experimental data［J］.China Civil EngineeringJournal， 2014，47(10):88-95.

［13］ 马建，孙守增，杨琦，等.中国桥梁工程学术研究综述·2014［J］.中国公路学报，2014，27(5):1-96.MA Jian，SUN Shouzeng，YANG Qi，et al.Review on China's bridge engineering research:2014［J］.China Journal of Highway and Transport，2014，27(5):1-9.

［14］ 江祥林，程高.基于EfI法的桥梁模态测试中传感器优化布置［J］.桥梁建设，2012，42(2):59-65.JIANG Xianglin， CHENG Gao. Optimalsensor placement forbridgemodaltestingbased on efi method［J］.Bridge Construction， 2012， 42(2):59-65.

［15］ 唐勇，陈志坚.大型群桩基础安全监测传感器选型优化［J］.西南交通大学学报，2011，42(2):247-251.TANG Yong， CHEN Zhijian. Sensor selection optimizaion for monitoring system of large-scale grouppile foundation［J］.JournalofSouthwestJiaotong University，2011，42(2):247-251.

［16］ LI B B，LI D S，ZHAO X F，et al.Optimal sensor placement in health monitoring of suspension bridge［J］. Science China: Technology Sciences，2012，55(7):2039-2047.

［17］ MOORE E Z，MURPHY K D，NICHOLS J M.Optimized sensor placement for damage parameter estimation: experimental results for a cracked plate［J］. Structural Health Monitoring， 2013，12(3):197-206.

［18］ LIU W，GAO W C，SUN Y，et al.Optimal sensor placement for spatial lattice structure based on genetic algorithms［J］.Journal of Sound and Vibration，2008，317:175-189.

［19］ 王海龙，刘杰，王新敏，等.建立斜拉桥基准有限元模型的新方法与实现［J］.振动·测试与诊断，2014，34(3):458-462.WANG Hailong，LIU Jie，WANG Xinmin，et al.A new method and it's implementation ofbuilding baseline FE model of cable-stayed bridge［J］.Journal ofVibration， Measurement ＆ Diagnosis， 2014，34(3):458-462.