双机械手协同运动模型及其工作空间分析

李 情，茅 健，朱姿娜，周玉凤

（上海工程技术大学 机械工程学院，上海 201620）

0 引言

现代工业的发展和机械手技术的进步使得机械手的性能不断提高，机械手应用的领域和范围正不断扩展。为了适应不断提高的任务复杂性、操作智能性以及系统柔顺性等要求，双机械手乃至多机械手之间的协调和协同作业是机械手技术在工业环境中进行推广和应用急需解决的关键技术之一[1]。

国内外对双机械手协调运动做了非常多的研究工作。在国际上，Clemson大学机器人实验室[2]，通过控制两台PUMA-560工业机械手来完成搬运实验；Duke实验室[3]，通过控制两台ABB-IRB140工业机械手来完成协调控制实验；PRISMA实验室[4]，通过控制两台SMART-3S工业机械手来完成协调插孔实验。在国内，沈阳自动化研究所采用分层结构，根据离散控制原理建立了多级机械手控制系统，该系统成功利用PUMA-560工业机械手和PUMA-760工业机械手完成了位置控制和轨迹控制协调实验[5]；东南大学通过控制两台型号为VA1400和HP20的YASKAWA工业机械手完成了双机械手协同焊接和搬运实验[6]。

机械手的工作空间是机械手末端执行器所能到达的范围，是机械手运动灵活程度的重要指标之一[7]，同时也是机械手是否有逆解的依据。对于双机械手工作空间的求解主要有图解法、解析法和数值法。图解法和解析法对于多自由度的机械手会有无法准确描述、计算繁琐等问题。数值法可以分析任意结构的机械手，而且随着计算机技术的发展得到了广泛应用[8]。

本文采用D-H变换矩阵法建立双机械手运动学模型，揭示机械手末端执行器在不同运动形态下笛卡尔坐标空间位姿与机械手各关节变量之间的转换关系。利用MATLAB中Robotics Toolbox建立双RCX340机械手三维仿真模型,验证运动学模型的可靠性。采用蒙特卡洛法对双机械手的工作空间进行分析，得到双机械手末端执行器的最佳协调工作空间。

1 双机械手运动学分析

单机械手与双机械手运动学分析的整体思路相似，不同的是双机械手需要考虑协同性与整体性。

1.1 双机械手坐标系的建立

本文以两台SCARA型机械手为研究对象，利用D-H参数方法中的关节方法建立各连杆的坐标系，如图1所示。首先取两机械手操作臂的中点为坐标原点（O0-X0Y0Z0），向两边增减平移坐标至两机械手底座中心点，两机械手基础坐标系分别记为Pl-XlYlZl和Pr-XrYrZr，即为各个底座为分坐标中心，然后依次向上延伸至各个关节处，其中L1、L2、L3与R1、R2、R3分别代表两末端不同运动形态的机械手传动轴。双机械手各连杆D-H参数如表1所示。

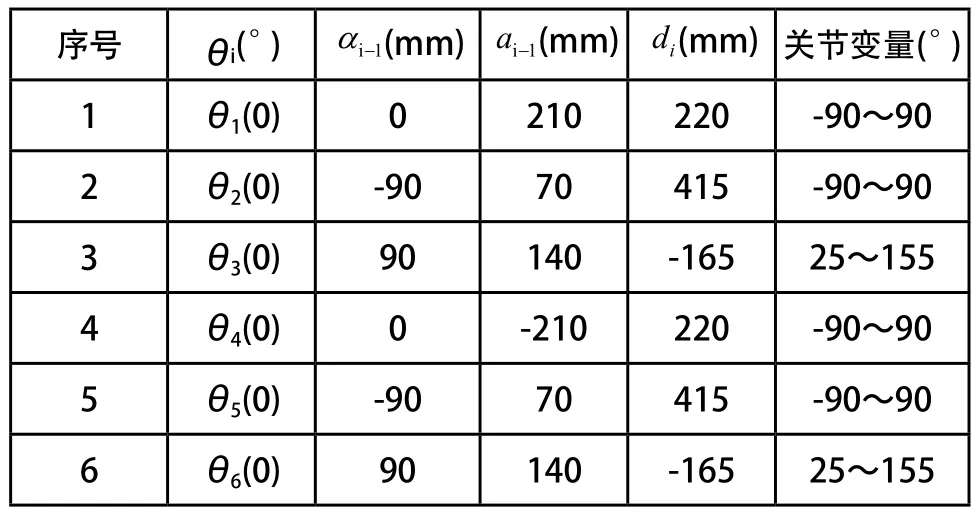
表1 双机械手连杆的D-H参数

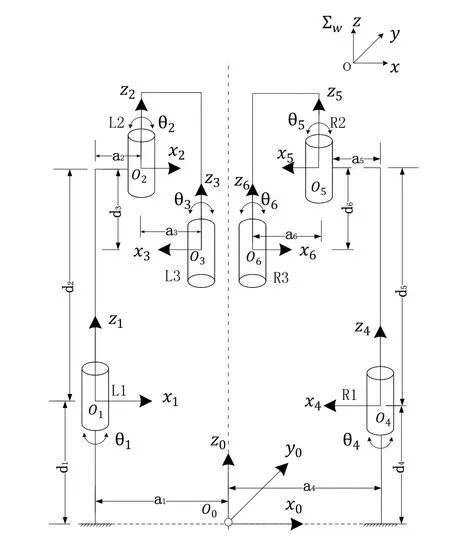
图1 双机械手运动关节结构图

1.2 正向运动学模型

机械手的正向运动学是指由给定的关节值求解机械手手部位姿。在机器人学中，机械手的手部姿态和位置可以用4×4阶矩阵来表示：

其中为手部接近矢量；为手部姿态矢量；为手部法相矢量。此三个矢量构成右手矢量级，即手部位置可以用从基础参考系原点指向手部中心的矢量来表示，这里，为手部在基础坐标系中的坐标。

用A矩阵描述一杆件和下一杆件之间的齐次变换关系，用Denavit-Hartenberg法得到连杆变换的一般表达式为：

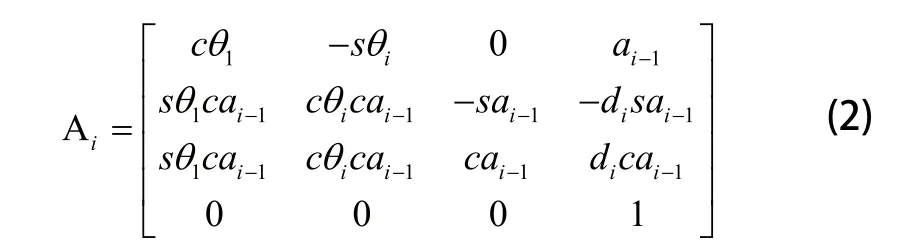
将D-H参数表中的数据带入连杆变换通式中得到相邻连杆坐标系之间的齐次变换矩阵为：

末端执行器在基础坐标系位置：

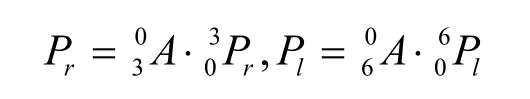
这样可得到双机械手末端执行器正向运动学模型，即：

1.3 逆向运动学模型

从应用研究的角度来说，逆向运动学是机械手运动规划和轨迹控制的依据。求解逆运动学问题是已知机械手末端执行器的坐标位置来计算机械手各个关节的角度值，是正向运动学问题的反过程[9]。求解过程复杂：

利用逆变换左乘式(1)两边：

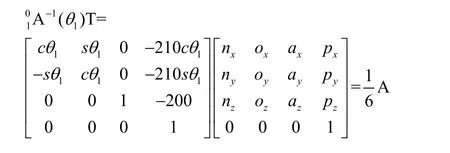
根据三角代换和矩阵的相关运算可依次得出：

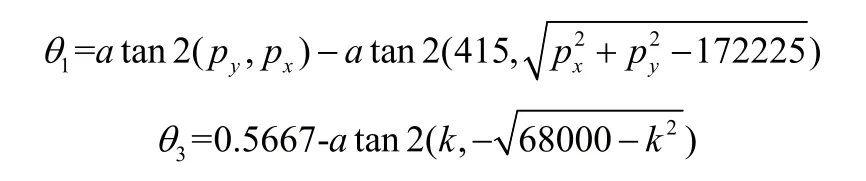
式中：

因双机械手为并联对称放置，故同型号的两个机械手的关节角度值分别相同，即：

2 双机械手模型建立与分析

2.1 模型的建立

在MATLAB中建立双RCX340机械手模型，如图2所示。

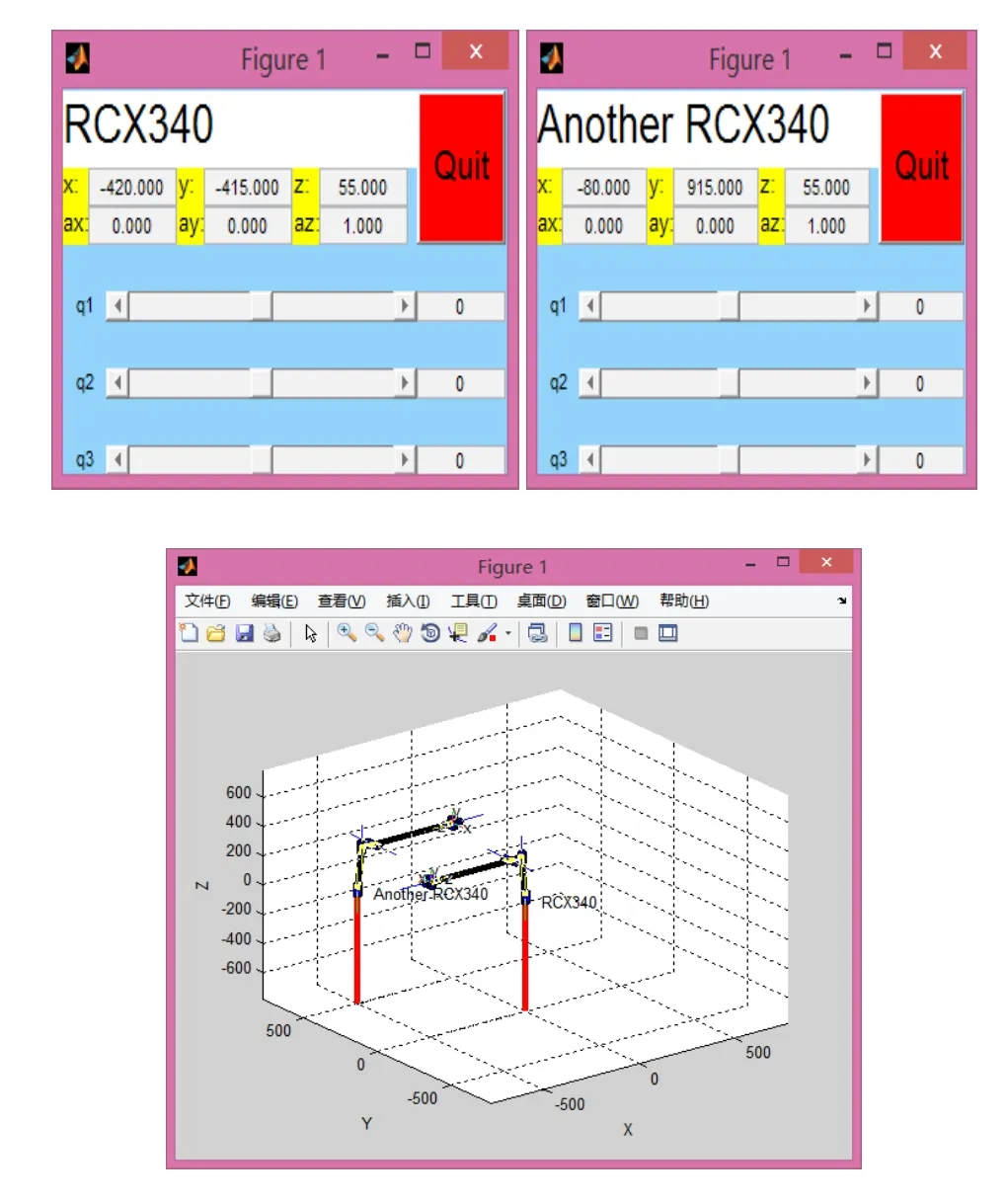
图2 基于Robotics toolbox的双RCX340机械手模型

2.2 双机械手模型分析

通过移动图2中代表关节角度的左右各3个滑块驱动双机械手运动，左右滑块q1、q2的移动可以改变RCX340和AnotherRCX340的末端执行器的位置，左右滑块q3的移动可使末端执行器具有不同的姿态。为验证运动学方程式的正确性，把机械手各杆件的几何参数和3组随机选取的关节变量值代入运动学方程，求得末端执行器的位姿；然后将相应的数据输入到双机械手滑块控制面板中直接读取实际的末端执行器的位姿数据并进行比较。随机选取的3组关节变量值如表2所示。

滑块控制面板直接读取的值和双机械手末端执行器的方程求解数据比较如表3和表4所示。

表2 三组随机关节变量

从表3中可以看出，随机变量代入运动学方程求取的正解和滑块控制面板直接读取的末端坐标数值相比误差较小，而从表4中不仅可以看出运动学逆解和滑块控制面板读取的关节角度数值误差较小，还可以看出同型号对称放置的左右机械手对应关节角度值也是相同的。因此，验证了所求解的运动学方程和利用函数建立的机械手三维模型的可靠性。

3 双机械手工作空间分析

机械手的活动范围是由其工作空间的大小所决定的，其形状和尺寸在机械手设计和优化等方面具有重要意义[10]。蒙特卡洛法基于随机理论，是常用的求解机械手工作空间的数值方法，其基本思想是：机械手的各关节是在其相应取值范围内工作的，当所有关节在相应取值范围内随机遍历取值后，末端点的所有随机值的集合就构成了该机械手的工作空间[11]。

利用蒙特卡洛法求取工作空间的步骤如下：

1）根据机械手运动学正解，求出机械手末端执行器相对于基座坐标系的位置向量P=[px, py, pz]。

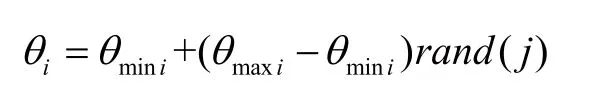
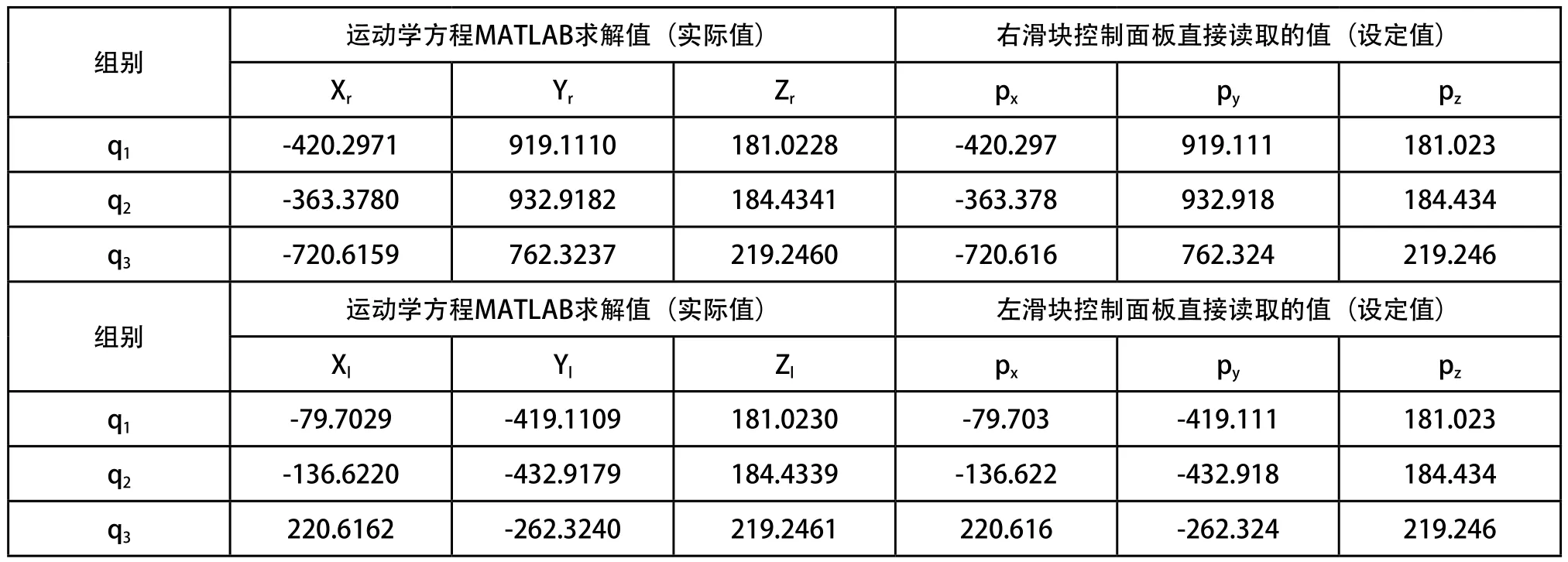
表3 运动学方程MATLAB正解值与两滑块设定值比较

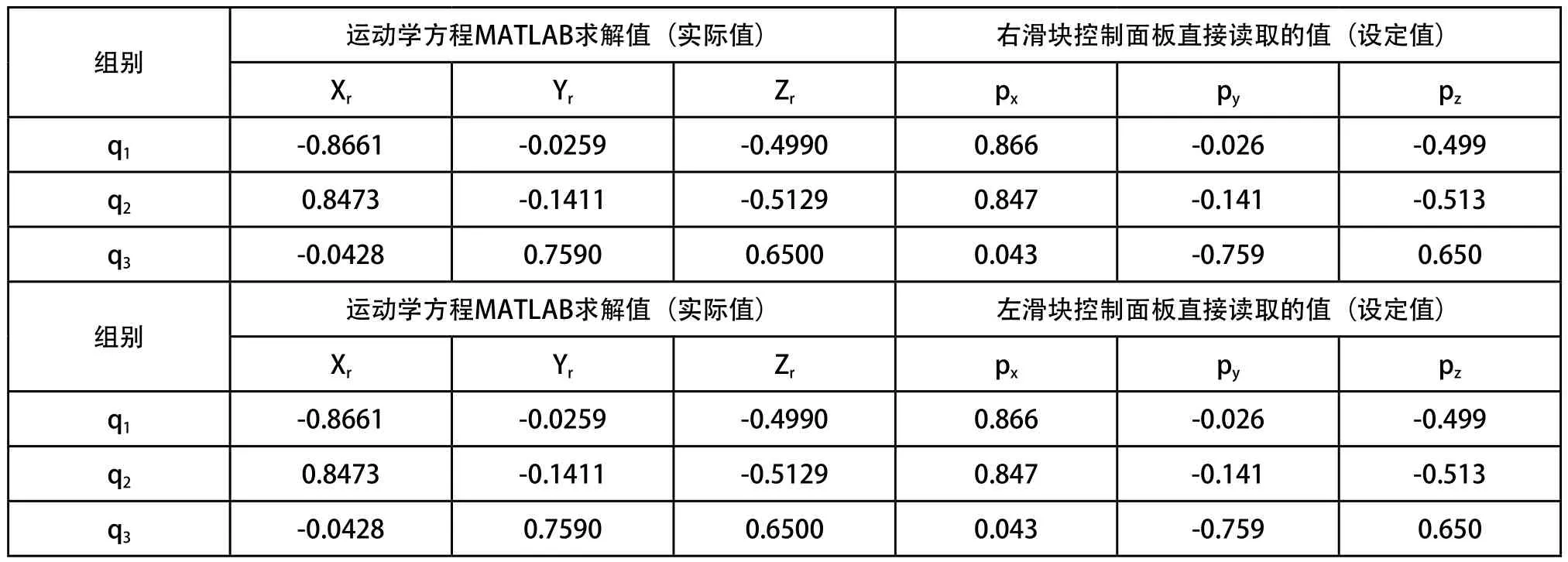
表4 运动学方程MATLAB逆解值与两滑块设定值比较

3）将N个关节变量伪随机值组合代入末端执行器的位置向量P=[px, py, pz]，并将其对应的x坐标、y坐标、z坐标分别存于矩阵X、Y和Z中；坐标值数目越多，结果就越接近双机械手的实际工作空间。

4）将所得位置向量的值用描点的方式显示出来，即可形成双机械手工作空间。取N=100000，D=900，利用蒙特卡洛法在MATLAB中求解双机械手的工作空间如图3所示。

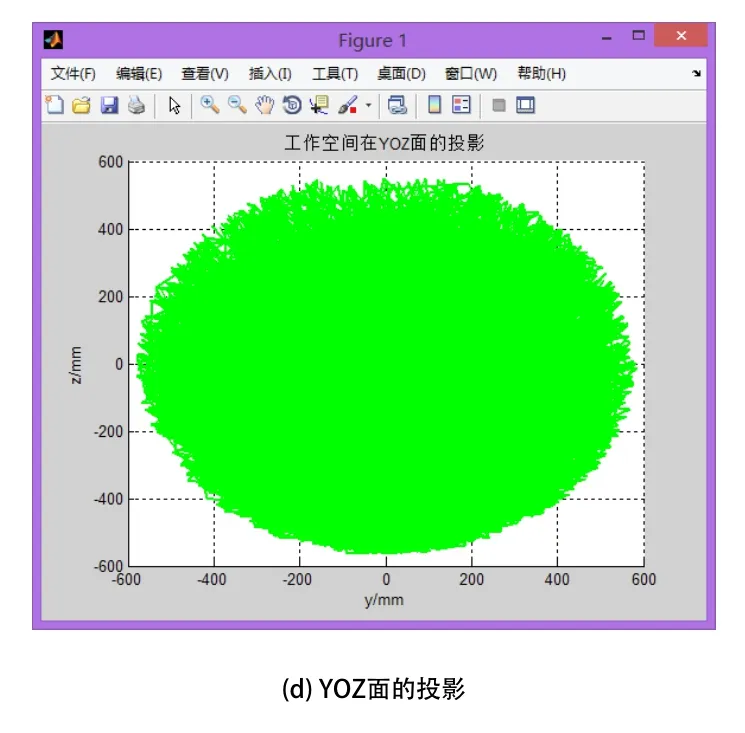
图3 双机械手工作空间

从图3可知，模拟出双机械手工作空间的形状近似两个椭球体相融，相融部分为双机械手协调操作的最佳协调工作空间，末端执行器最佳协调工作空间沿X轴的范围为（-130，130），沿Y轴的范围为（-360，360），沿Z轴的范围为（-350，350）。利用边界条件和蒙特卡洛法，进而模拟出双机械手最佳协调工作空间的仿真图，如图4所示，模拟出的最佳协调工作空间为双机械手协调轨迹规划提供了理论依据。

【】【】

图4 双机械手最佳协调工作空间

4 结论

本文建立了双机械手运动学模型，揭示了机械手末端执行器在不同运动形态下笛卡尔坐标空间位姿与机械手各关节变量之间的转换关系。仿真结果验证了所建立的双机械手运动学方程和基于Robotics Toolbox构建的三维模型的可靠性，直观地分析了机械手末端执行器位姿和各关节转角之间的关系。同时，采用蒙特卡洛法对双机械手工作空间进行了分析，得到双机械手末端执行器的最佳协调工作空间，为双机械手协调轨迹规划提供了理论依据。

[1]欧阳帆.双机器人协调运动方法的研究[D].广州：华南理工大学,2013.

[2]Alford C, Belyeu S. Coordinated control of two robot arms[A].IEEE International Conference on Robotics and Automation.Proceedings.IEEE[C],2003：468-473.

[3]Kumar M, Garg D P. Fuzzy logic based control of multiple manipulators in a flexible work cell[A].IEEE International Symposium on Intelligent Control[C].IEEE Xplore,2003：399-404.

[4]Caccavale F, Natale C, Siciliano B, et al. Achieving a cooperative behavior in a dual-arm robot system via a modular control structure[J].Journal of Robotic Systems,2001,18(12)：691-699.

[5]曲道奎,谈大龙.双机器人协调控制系统[J].机器人,1991,13(3)：6-11.

[6]张曦.多机器人协作焊接系统的算法研究与仿真实现[D].南京：东南大学,2015.

[7]田海波,马宏伟,魏娟.串联机器人机械臂工作空间与结构参数研究[J].农业机械学报,2013,44(4)：196-201.

[8]Cao Y, Lu K, Li X, et al. Accurate Numerical Methods for Computing 2D and 3D Robot Workspace[J].International Journal of Advanced Robotic Systems,2011,8(6)：1-13.

[9]范叔炬.机械臂运动学算法设计[D].杭州：浙江大学理学院 浙江大学,2008.

[10]刘志忠,柳洪义,罗忠,等.机器人工作空间求解的蒙特卡洛法改进[J].农业机械学报,2013,44(1)：230-235.

[11]李瑞峰,马国庆.基于Matlab仿人机器人双臂运动特性分析[J].华中科技大学学报自然科学版,2013,41(s1)：343-347.