基于轻量化的全地形巴哈赛车车架设计与优化
陶 超,马其华,黄天柱,黎劲宏
(1.上海工程技术大学 汽车工程学院,上海 2016202;2.西安建筑科技大学 机电工程学院,西安 710055;3.东华大学 机械工程学院,上海 201620)
0 引言
全地形赛车要求各参赛队按照赛事规则和赛车制造标准,在规定时间,使用同一型号发动机,设计制造一辆单座、发动机中置、后驱,完成各种严厉路况要求考验的小型越野车。由于在全地形路面上赛车受到的振动、冲击等影响更大,而这些影响将直接反应到车架上,所以车架的模态及刚强度要求需要经过严格分析,以满足要求。
利用有限元分析法对全地形赛车车架进行评价分析,对于保证设计可靠性和一致性具有重要作用。汪俊[1]等对某方程式赛车车架做了满载弯曲、满载加速、满载转弯和扭转工况下的强度和刚度分析,并通过分析结果对车架钢管尺寸进行了优化,减轻了车架重量;周明华[2]等对某农用车车架进行自由模态分析,得到车架的前6阶弹性模态振型及频率特性,从而验证了该车架结构设计的合理性;陈旭[3]等计算了某全地形车架的自由模态,并对比实验模态频率,验证了有限元模型及其分析结果的正确性。以上的研究对于常规行驶条件分析已经比较完善了,对于适应全地形要求的赛车车架设计需要根据实际情况提出对保证轻量化的情况下车架设计的可靠性要求。本文从全地形路况对赛车性能的影响出发,运用有限元分析法探讨了全地形巴哈赛车车架进行优化设计方法。
1 多条件要求下的巴哈赛车车架设计
全地形巴哈赛车的赛道由单驼峰、飞坡、炮弹坑、连续弯道、泥坑、双驼峰、轮胎阵、三驼峰、乱石堆等恶劣路况组成,赛车行驶过程中受到的振动和冲击将通过悬架直接传到车架上,故对车架设计要求更高。赛规要求车架结构必须由直或弯曲的钢管组成,两个支撑点之间的直管结构件必须足够支撑整个车架的受力,同时长度不得超过711mm。
驾驶舱前部是安放转向机构、前刹车制动缸及其管线的位置,驾驶舱后部是安放发动机、CVT、减速器、差速器、半轴、排气装置、后刹车制动缸及其管线等部件。要保证这些零部件及其总成有足够的安装位置和合适的安装点,并且能合理高效的利用有效空间,使得巴哈赛车整体布局紧促合理。车架的设计还需要考虑安装好上述所有零件及总成后,整车总宽即后轮两轮胎外侧的直线距离不超过1620mm。车架与整车装配如图1所示。
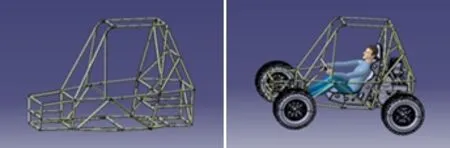
图1 车架与整车装配模型
2 巴哈赛车车架的有限元分析
2.1 赛车车架有限元模型的建立
将车架的几何模型导入到HyperMesh有限元建模软件中,通过对模型做几何清理并画出满足有限元分析要求的网格。巴哈赛车车架由等厚度的薄壁管件构成,所以选用2D壳单元的结构作为车架网格的结构单元类型,单元的尺寸设置为3mm,网格的类型设置为四边形和三角形混合网格。建立车架有限元模型如图2所示。
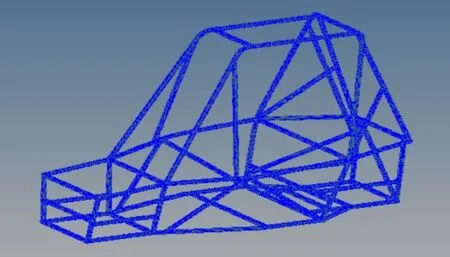
图2 车架有限元模型
2.2 车架自由模态分析
分析巴哈车架的前12阶固有频率,由于前6阶为刚体模态,故提取第7阶到第12阶的6阶模态进行分析,并将第7阶频率记为第1阶,如表1所示。第1、2阶振型如图3所示。
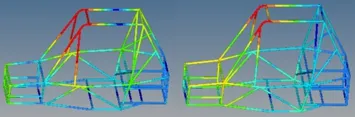
图3 一、二阶模态振型图
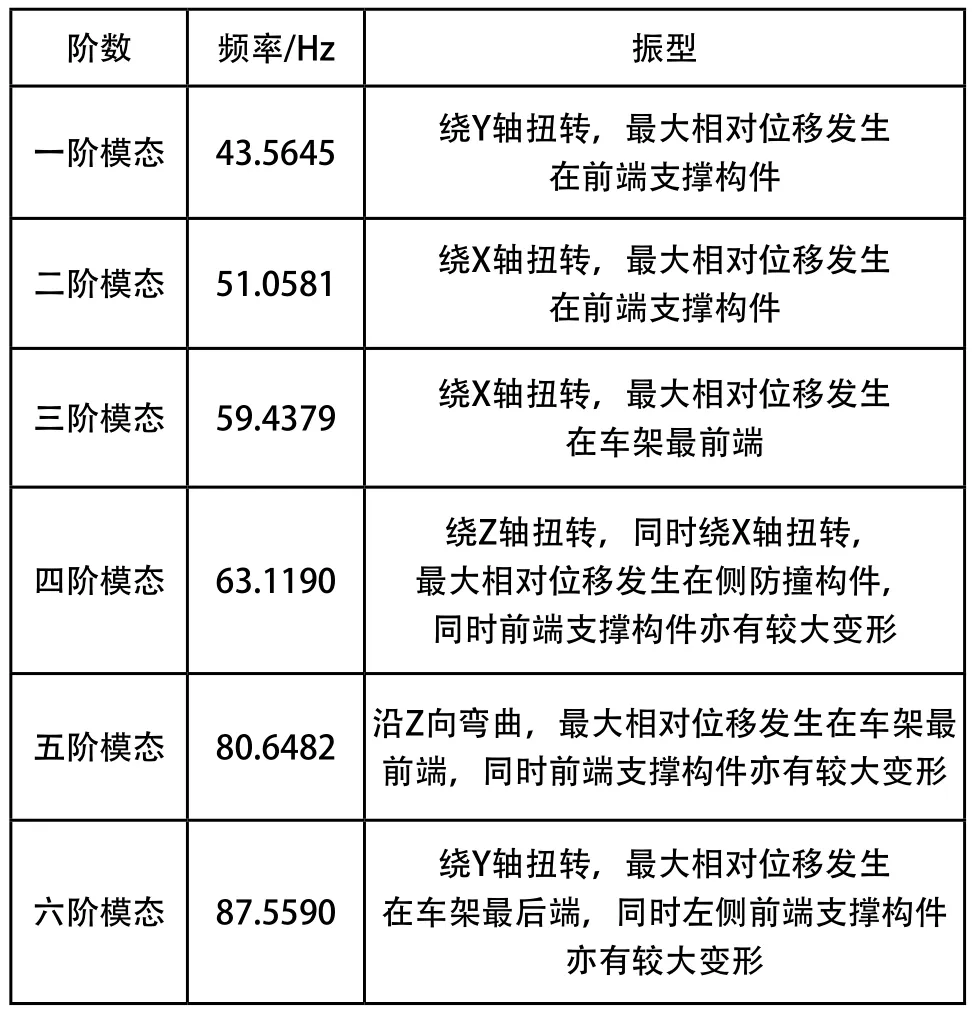
表1 前6阶自由模态的固有频率和振型
巴哈赛车在行驶过程中主要受到两种外部激励:
1)来自各种复杂路面凹凸不平的激励传到车架会导致车架振动,全地形车悬架系统弹簧以上的部分质量偏频大致在2~3Hz,簧下质量的偏频大约在20Hz以下[4]。远远低于车架的固有频率,故不会发生共振;
2)由发动机在不同工作状态内部产生的振动。赛车在怠速、正常行驶和加速等不同工况下的发动机转速不同,不同转速下的激振频率可由下式求得。
本赛车选用的是指定的百利通M20单缸四冲程风冷发动机,其转速从怠速到最高转速的范围是2000~3600r/min,经式(1)计算得振动频率范围为16.67~30Hz,因为其频率低于车架的固有频率,故不会发生共振。
2.3 满载弯曲工况分析
满载弯曲工况指的是赛车在满负载的状态下,前、后四个车轮均着地,在平坦道路上行驶时的工况。此时约束后悬架Y向,前悬架X、Y、Z向的平动自由度。在此工况下,取动载系数1.8,车架受到的力的大小为所有载荷乘以动载系数,方向为Y方向。
车架自重等效点即重心位置处施加的合力为:

驾驶员质量等效点即驾驶员重心处施加的合力为:

发动机及传动系统等效点即其重心处施加的合力为:
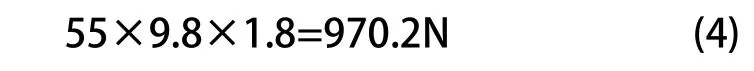
将上述的力作用到巴哈车架上。
由图4可以看出,在满载弯曲工况下,巴哈车架最大应力值为55.05MPa,出现在发动机及传动系统在车架上的安装位置,小于4130钢的屈服极限386Mpa;巴哈车架最大位移量为0.036mm,远小于赛规要求的最大允许挠度,该位移出现在座椅在车架上的安装位置。
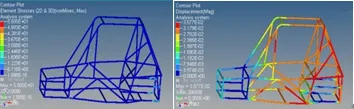
图4 满载弯曲工况下车架应力、位移云图
2.4 急转弯工况分析
当巴哈赛车在转弯时会产生指向转弯半径圆心的向心力,在向心力的作用下,车架会承受侧向荷载,同时在急转弯时还存在一个纵向制动力[6]。在一个急转弯实际赛车的向心力是很难计算的,而且向心力和汽车的速度及转弯半径的大小有关,因此我们选择重力加速度g(9.8m/s2)为向心加速度。赛车的制动减速度等于重力加速度和制动力系数的乘积,制动力系数取0.6,动载系数取1.5。因此,车架受到向心力为:
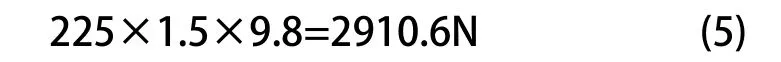
车架受到制动力为:
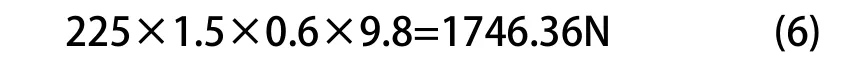
车架受到的制动力和向心力的作用点在前悬架和后悬架的约束点处[7]。同时约束前悬架X、Y向的平动自由度,左后悬架Y向及右后悬架X、Y、Z向的平动自由度。
由图5可以看出,在急转弯工况下,巴哈车架的最大应力为243.5MPa,小于4130钢的屈服极限386MPa,该应力出现在车架底部与后部防滚环连接点处;巴哈车架最大位移量为6.17mm,小于大赛要求的最大挠度,该位移出现在前悬架的安装位置。
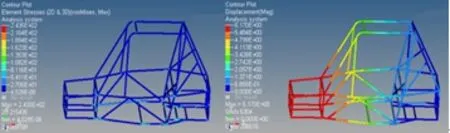
图5 急转弯工况下车架应力、位移云图
2.5 紧急制动工况分析
紧急制动时,赛车车架承受的力将和行驶方向相反。据文献[5],赛车以减速度进行制动,制动力在前后轮上的分配比为7:3,动载荷系数取1.6,故整车制动力为:
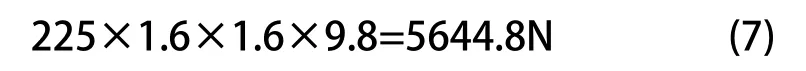
前轮制动力为:
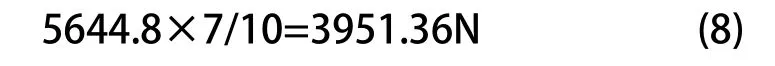
后轮制动力为:
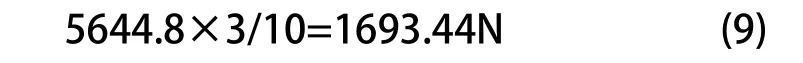
本文将制动力作用在前后悬架的连接点处。约束前悬架X、Y、Z向的平动自由度及后悬架Y、Z向的平动自由度。
由图6可以看出,在紧急制动工况下,车架最大应力为37.79MPa,远小于4130钢的屈服极限386MPa,该应力出现在后悬架与车尾连接点处;车架的最大位移量只有0.151毫米,比大赛要求的最大挠度要小很多,该位移出现在左后悬架的安装位置。
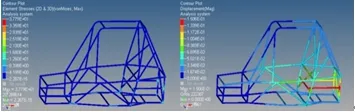
图6 紧急制动工况下车架应力、位移云图
2.6 强度校核
巴哈车架整体强度的安全系数是车架材料4130合金钢管的屈服极限值与车架在不同工况下计算出来的最大应力值之比。当安全系数>l时,说明巴哈车架的强度符合要求,在行驶过程出不会出现问题,安全可靠[8];当安全系数<l 时,说明车架的强度不满足要求,车架很可能在行驶过程中发生损坏,这是不被允许的[9];但是安全系数太大也不好,这说明对材料的利用率太低,一般情况下不大于2.5。巴哈车架再三种工况下的安全系数如表2所示。
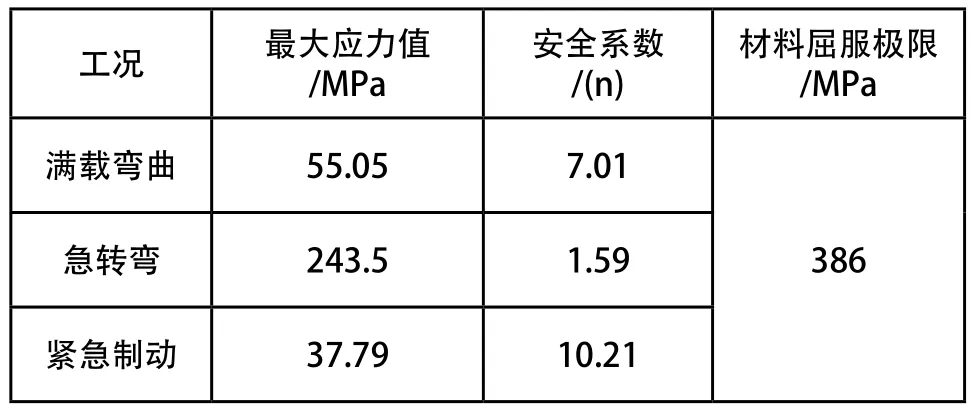
表2 巴哈车架在三种工况下的安全系数
对比表2中的安全系数,可见车架安全系数过于保守,最小的安全系数也有1.59,最大达到了10.21,这说明车架整体的强度、刚度富冗余太大,需要进行优化。
3 巴哈赛车车架的轻量化优化
3.1 车架钢管尺寸的DOE优化
DOE(Design Of Experiment)技术方法提供了运行一系列试验的计划和分析工具。在HyperStudy中实现DOE的基本过程为:首先通过设定目标函数来确定试验的评价目标;然后确定一套试验方案,随后运行设计好的试验方案得到DOE设计结果,最后通过分析结果确定最终的参数匹配方案[10,11]。HyperStudy中的DOE技术可采用用户自定义的试验矩阵,也可采用全因子试验法,本文采用的是全因子试验法。
结合有限元分析结果将车架所用钢管的尺寸分为主要部件和次要部件,图7中红色部分为主要部件,绿色部分为次要部件。
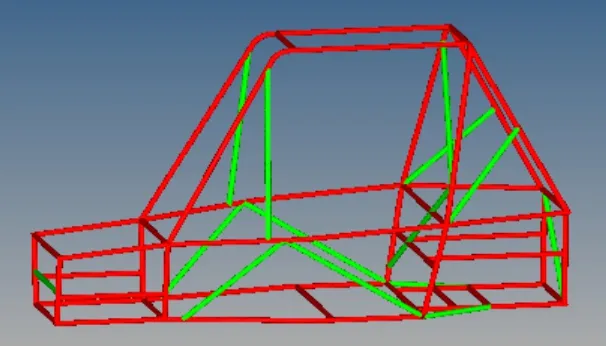
图7 车架的主要部件和次要部件
通过对静力分析结果及整车要求建立两个响应。第一个响应为在保证强度、刚度的基础上使质量最小;因为在急转弯工况下,最大应力值最大为243.5Mpa,安全系数为1.59,故我们建立第二个响应为在急转弯工况下的最大应力值在160Mpa和320Mpa之间,即安全系数在1.2和2.5之间。计算结果如表3所示。
根据计算结果,同时结合现在市面上能够买到的4130合金钢管的尺寸,将2.6mm壁厚的钢管作为主要部件,1.5mm壁厚的钢管作为次要部件。原车架的总质量达到了66.2kg,优化后车架总质量52.3kg,前后相比减轻了13.9kg。
3.2 优化前后车架模态结果对比
计算优化车架的前12阶固有频率,去掉前6阶刚体模态,并将第7阶频率记为第一阶,对比优化前后车架的模态,如图8所示。
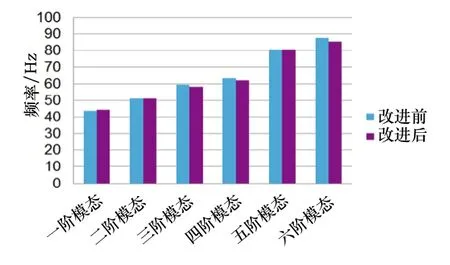
图8 优化前后车架模态结果对比图
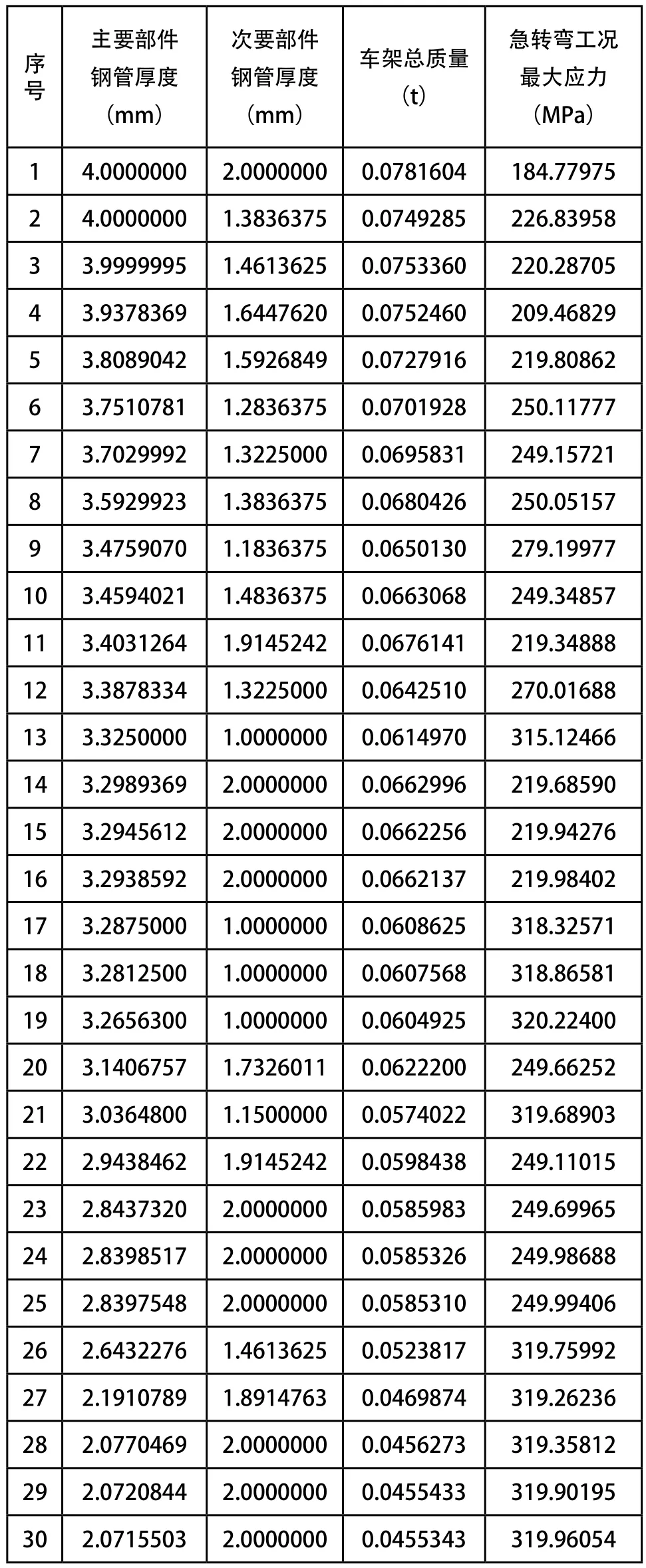
表3 HyperStudy计算结果
优化前后车架各阶模态固有频率数值变化不大,在4Hz以内,且远高于各激振源频率,说明新优化的巴哈车架在实际使用时不会发生共振现象,动态特性理想。
【】【】
3.3 优化后车架各工况分析
改变原车架有限元模型的各部分钢管厚度(主要部件2.6mm,次要部件1.5mm)后再做一次满载弯曲工况、急转弯工况和紧急制动工况,其约束和受力情况与原车架相同。分析结果如图9所示。
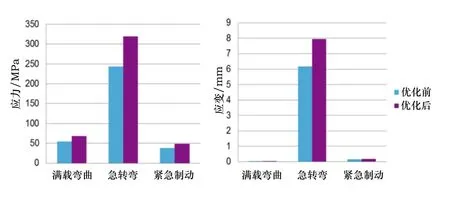
图9 优化前后各工况最大应力应变对比图
通过对比各工况计算结果,可以看出优化后车架的应力应变分布更加均匀,刚强度富余量明显减小,虽然使用了更薄的钢管,但三个工况中出现的最大应力值319.8MPa,也比4130钢管的屈服极限更低。且安全系数更加合理,表明优化车架的设计安全合理,同时也达到了节约材料、降低车架重量的目的。
4 结论
本文通过对全地形巴哈赛车车架的设计、分析及优化,得出以下结论。
1)通过人体工程学分析及整车装配,使得设计的车架能满足实际使用要求。
2)在车架刚强度均有冗余的情况下,采用DOE技术对车架进行尺寸优化,优化后车架重量由66.2kg下降到52.3kg,前后相比减轻了13.9kg,轻量化效果明显。
3)通过模态分析,保证赛车在行驶中车架不会与其他激振频率发生共振,动态性能良好。
4)通过各工况的静力分析,计算结果表明车架应力应变在要求范围内,设计安全合理。
针对此全地形赛车车架的设计、分析及优化流程,可以推广并应用到其他钢管桁架式车架的开发中。
[1]汪俊,马雷廷.基于Hyperworks的FSAE车架有限元分析及优化[J].AGRICULTURAL EQUIPMENT & VEHICLE ENGINEERING,2014,52(8).
[2]周明华,李红,骆群.全地形车车架的有限元建模和模态分析[J].机械工程与自动化,2015(6):34-35.
[3]陈旭,娄威振,蒋亚东.全地形车车架静动态特性分析与轻量化设计[J].重庆理工大学学报:自然科学版,2015,29(2):1-6.
[4]黄云涛.全地形车车架动态特性分析与结构优化[D].重庆理工大学,2015.
[5]于淼,杜俊廷,鲁植雄.基于ANSYS的FSC车架有限元分析[J].农业装备与车辆工程,2014,52(9):20-22.
[6]赵帅,隰大帅,王世朝.FSAE 赛车车架的强度和刚度分析[J].计算机辅助工程,2011,20(4):53-56.
[7]赵帅,隰大帅,王世朝.FSAE赛车车架的强度和刚度分析[J].计算机辅助工程,2011,20(4):53-56.
[8]许佩霞,蔡炳芳.基于ANSYS的全地形车车架结构优化设计[J].机械设计,2008,25(12):56-58.
[9]张心光,高宾,王岩松.基于不同工况下的FSC赛车车架有限元分析[J].制造业自动化,2015,37(19):44-46.
[10]Christopher Scott Baker. FOES Formula SAE-A Space Frame Chassis Design[J].Master Dissertation of University of Southern Queensland,2004.
[11]LuqueP, MantarasD.A.Pneumatic suspensions in semi-trailers[J].Heavy Vehicle Systems,2003(10):309-320.

