一种提高伺服控制系统性能的设计方法

史红伟，单泽彪，王春阳，牛启凤

（长春理工大学 电子信息工程学院，长春 130022）

伺服控制系统是高精密加工设备的关键部分，伺服控制的性能对设备整体性能影响很大。目前国内的高端数控设备严重依赖进口，与国外先进设备整体差距比较大。随着“中国制造2025”的部署和实施，需要大力投入精力提升我国高端制造业的竞争力。精密加工设备性能可以从优化机械设计、提升制造工艺等方面入手。本文从伺服控制系统控制器算法设计入手，通过采用先进的控制算法来提升伺服系统的性能，进而提升设备整体性能。

PID［1］控制自诞生之日就一直主导着工业的各行各业。但是传统的PID控制是基于误差来消除误差，是典型的被动控制技术，即只有扰动作用于系统产生了误差，控制器才能产生控制量来消除误差。而现代控制理论框架下，解决不确定问题往往需要被控对象精确的数学模型，而实际中被控对象的数学模型往往不可得，或者需要很高的成本来建立模型［2］。最优控制、神经网络等控制方法设计难度大、计算复杂，成本较高不易在实际工程中得到推广和应用。

自抗扰控制（ADRC）［3-6］技术弥补了经典PID和现代控制理论的缺陷，吸收了现代控制理论成果并发扬丰富了PID思想精髓（基于误差来消除误差）。它不依靠被控对象准确和详细的动态模型，能从被控对象的输入和输出信号中把扰动信息提取出来，然后以这个信息为依据，想办法在扰动影响系统之前用控制信号把它消除掉。ADRC可以处理大范围及复杂结构（非线性、时变、耦合等）不确定系统，且控制结构简单并可保证闭环系统具有良好的动态性能［7］，并在一些仿真实验［8］和实际工程中得到应用［9］。

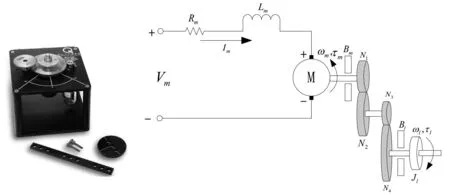
图1 SRV02伺服旋转装置及结构简图

本文针对伺服控制系统的位置控制，设计了自抗扰控制器，与传统的PID控制器进行多方面的仿真与实验对比，在Quanser半实物仿真平台进行了实际验证。本次设计还提供了在已知被控对象部分模型信息时的LESO设计方法。实验表明，LADRC控制器能够使系统获得更好的鲁棒性。

1 Quanser系统简介及建模

Quanser SRV02旋转伺服装置是加拿大Quanser公司开发的半实物仿真平台。该实验装置包括支撑框架、直流电机、齿轮箱、高精度光电编码器等。可通过更换齿轮来改变传动比，外加负载来改变转动惯量。配合提供的Quanser RCB工具包，可在上位机中使用MATLAB软件来进行算法设计。通过数据线在上位机和SRV02装置建立通信，上位机会显示半实物平台运动状态信息，同时上位机会根据监测到的数据作为控制器对伺服驱动器发出电机控制信号，形成闭环控制，如图2所示。

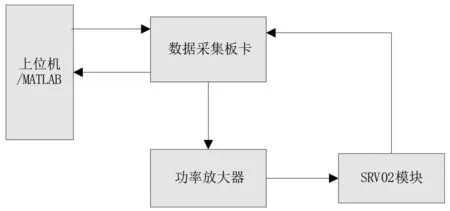
图2 SRV02半实物仿真平台结构图

本半实物仿真平台通过高精度编码器来获取伺服旋转装置的速度信息，通过数据采集板卡将速度信息送入计算机，通过运算得到其位置信息，把设定值和当前检测值做差，借由数据采集卡的输出端发出修正指令至功率放大器，驱动旋转装置电机运动。

SRV02负载角速度和电机输入电压可用一阶传递函数描述如下：

其中，Ωl(s)是负载角速度ω1(t)的拉普拉斯变换，Vm(s)是电机输入电压的拉普拉斯变换，K是稳态增益，τ是时间常数。

通过理论分析和推导，结合平台所提供的数据参数，可得平台的旋转角速度和输入电压的关系：

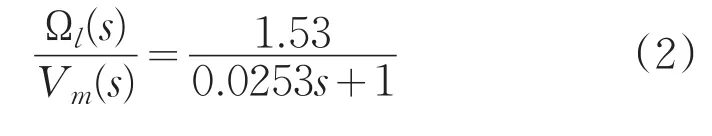
2 自抗扰控制器设计

自抗扰控制（ADRC）其结构主要包括合理安排过渡过程、非线性状态误差反馈律以及扩张状态观测器。扩张状态观测器是自抗扰控制器的核心，通过其动态补偿线性化作用，可将非线性对象转化为简单的积分器串联型结构，进而实施简易的误差反馈则可达到所期望的闭环动态。但是自抗扰控制器需要整定的参数过多，整定过程比较麻烦，难度较大。因此本文采用线性自抗扰控制器。

线性自抗扰控制技术是基于ADRC思想，以线性化实现形式设计各结构。该方法将控制参数简化为控制器带宽和观测器带宽的函数，而且都有比较明确的物理意义，十分便于工程应用，并且取得了很好的实际控制效果［10］。

扩张状态观测器（ESO）是ADRC的核心，ESO借助状态观测器的思想，它把系统模型的不确定性和外扰扩张成系统的一个新状态，估计出系统的总扰动，通过控制率来进行消除，从而实现“主动”抗扰。

通过对速度的积分，可获得负载的位置信息。现在对其进行位置控制其实也就是需要控制一个二阶对象。因此需要设计二阶自抗扰控制器。

平台的输入电压和负载位置关系的数学模型为：

将被控对象的传递函数形式，写成微分方程的形式为

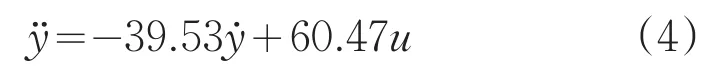
虽然ADRC不依赖于被控对象的数学模型，但如果知道对象的模型信息，并将其加以利用，可以提升控制器的性能［11］。本文提供了两种ESO的设计方法：分别是模型未知和已知时。

2.1 被控对象模型信息未知时LEO的设计

其中，y和u分别是输出和输入，即输出的位置和输入的电压，w是外部干扰。参数a1,a2都是未知的，b0是对控制增益b（本文中b0=60.47）的粗略估计。式5可写成：

被控对象5可写成状态空间的形式：

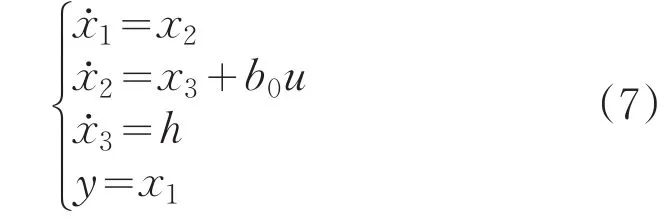
其中，x3=f，就是扩张出来的状态，h=ḟ。

建立其三阶线性扩张状态观测器：

其中，Z=[z1z2z3]T是对被控对象X=[x1x2x3]T的估计。

L=[β1β2β3]T是扩张状态观测器的误差增益。

将状态观测器特征方程的极点配置到-ωo。即：

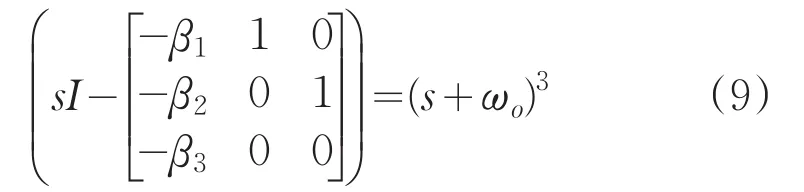
此时LESO为：

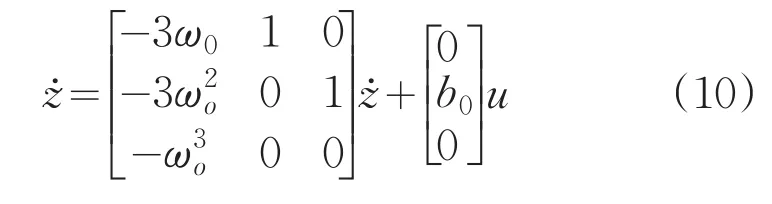
2.2 被控对象模型已知时的LESO设计方法

若被控对象模型信息已知，则可充分利用已知信息，提升控制器性能，文献［4］中提到了工程中的信息问题，应该充分利用已知信息来解决工程问题。本文中是将被控对象的已知模型信息加入到LESO的设计中，减小LESO的观测负担。此设计方法基于被控对象模型Model-Based Linear Active Disturbance Rejection Controller，称之为MLADRC。具体方法如下：

同样考虑二阶被控对象精确模型，表达式为4式。

考虑将被控对象的模型信息加入到扩张状态观测器的设计中，使其能够更加准确的估计不确定扰动信息。

被控对象其近似模型的状态空间形式表达如下：

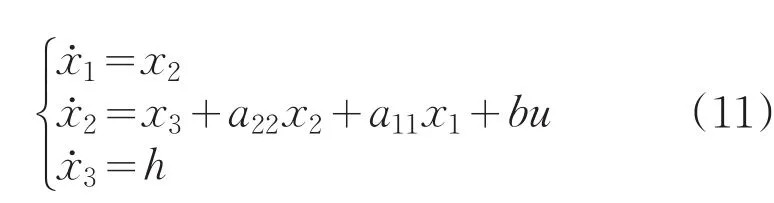
基于上述分析设计三阶扩张状态观测器：

解上式，可得扩张状态观测器的误差增益：

对应的扩张状态观测器为：

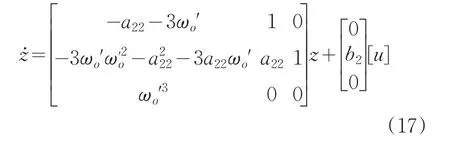
2.3 控制器设计

在模型信息完全未知的情况下，将外界扰动和模型的不确定性作为总扰动来进行观测和补偿，将被控对象改造成积分器串联型，采用简单的PD控制即可。文献［9］进行了详细说明和算例仿真本文不再赘述。

本文基于被控对象的近似模型信息，设计扩张状态观测器，补偿后的对象标准型不再是积分器串联型，而是如下16式的形式：

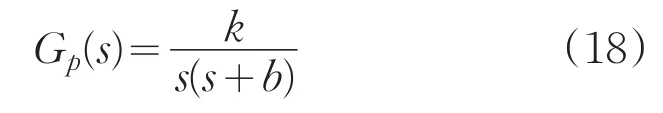
为了使被控对象的闭环传递函数的极点在一个位置，这样可方便控制器参数整定。期望的闭环传递函数如下式：

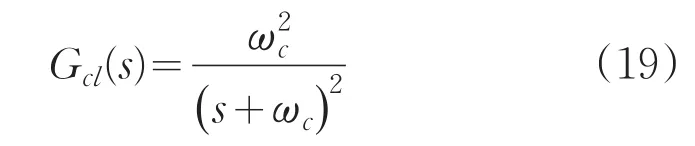
可推导出控制器：

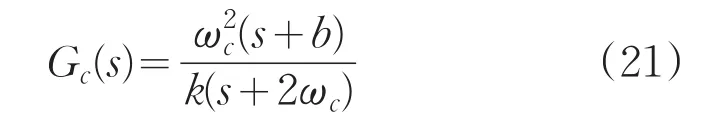
即控制器是关于ωc的函数。

2.4 算例仿真

一个二阶系统的模型为：

当取相同的扩张状态观测器误差增益时，

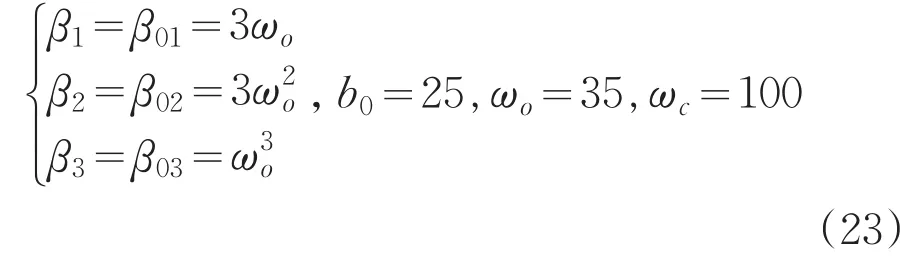
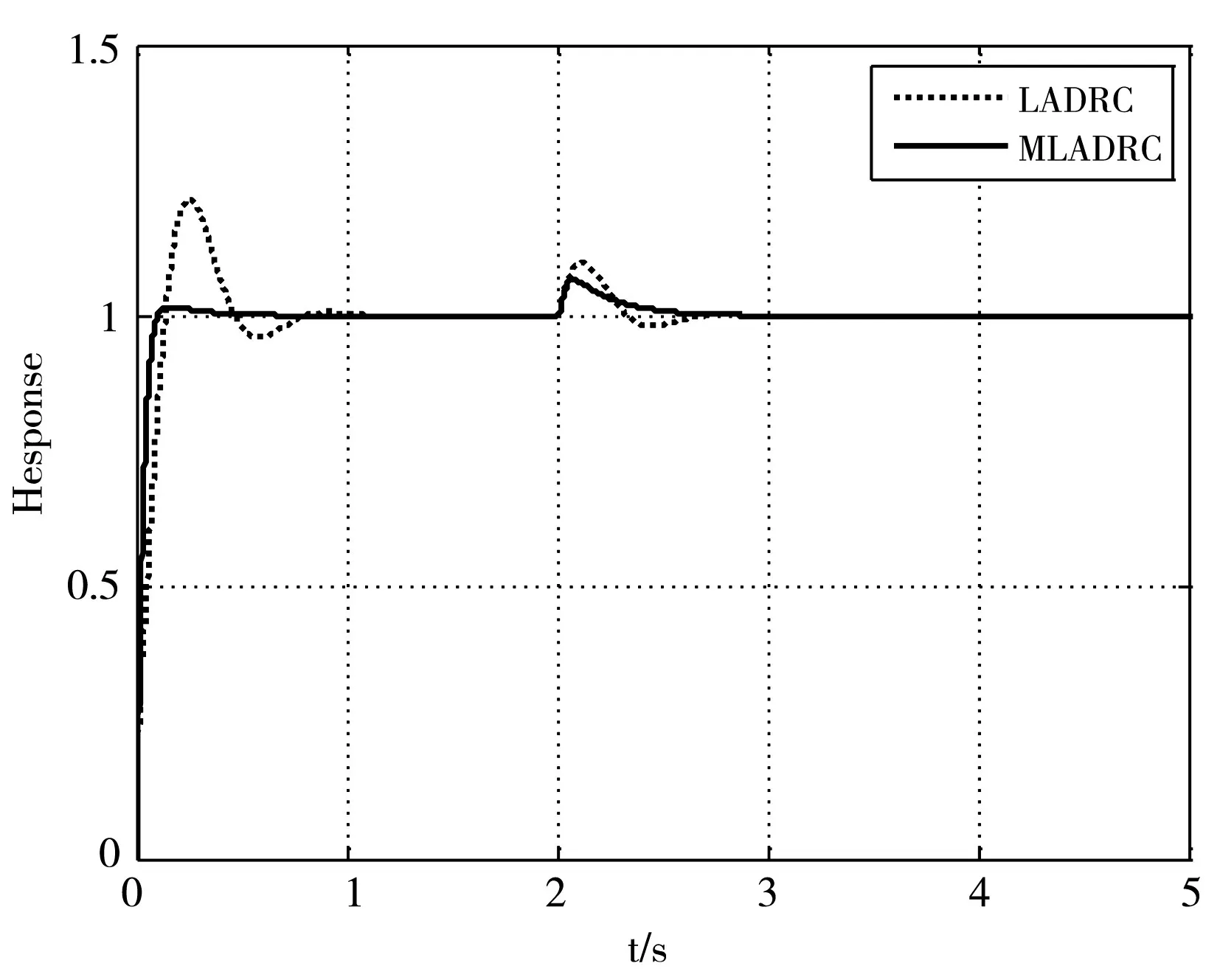
图3 添加扰动时阶跃响应

此时，如图3所示，MLADRC超调更小，无振荡，且进入稳态速度更快。在2s加入幅值为1的阶跃扰动信号，可看出MLADRC超调更小，对于扰动抑制效果更好，鲁棒性较强。

3 实验验证

为了评价自抗扰控制器的性能，设计一款PI控制器作为比较，在Quanser SRV02半实物仿真平台上进行实验。

同时还进行常规LADRC和基于模型信息的设计的新型MLADRC的性能比较实验。

3.1 LADRC和PI控制器的性能比较

一个高性能的控制器，不仅要能够使系统具有良好的额动态和静态性能，还要能够克服大范围的不确定性所带来的的扰动。

为了比较公平，使LADRC和PI控制器在相同的负载条件下可使系统获得系统的阶跃响应为标准，在不改变控制器参数的条件下，增加负载。

图4 改变负载时阶跃响应

从图4可看出，负载改变后，LADRC相较于PI仍然可使平台获得良好的动态和稳态性能，无超调且进入稳态时间更短。

3.2 LADRC和MLADRC性能比较

进行LADRC和MLADRC的控制性能对比，取相同的观测器增益和控制增益，在负载相同的条件系，进行SRV02伺服装置对位置的跟踪效果。

从图5可看出，添加模型信息后，实际实验结果与2.4中的仿真实验结果相同。

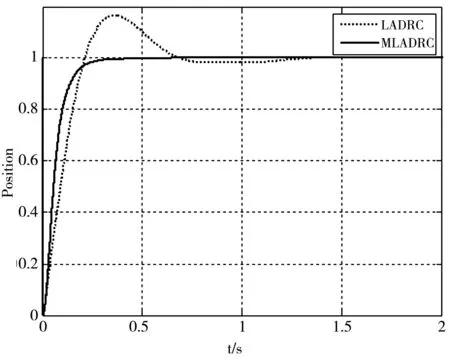
图5 阶跃响应

可看出，加入模型信息后，系统上升更快，超调更小，对扰动信息抑制效果更好，鲁棒性更强。

4 结论

本文通过设计伺服控制系统的线性自抗扰控制器，并在Quanser半实物仿真平台进行实验，与传统的PID控制方案进行对比。本文给出了在对象模型信息已知情况下的LADRC控制器设计方法。结果显示线性自抗扰控制器可以使伺服系统获得更强的鲁棒性，获得更好的性能。而且控制器设计简单，不依赖被控对象数学模型，具有一定的推广应用价值。

［1］Astrom KJ，Hagglund T.PIDcontrollers：Theory，design and tuning［M］.Instrument Society of Americna，1995.

［2］Gao ZQ.On Disturbance rejection paradigm in control engineering［C］.Proceedings of the 29th Chinese Control Conference，2010.

［3］Han JQ.The“extened state observer”of a class of uncertain system［J］.Control and Decision，1995，10（1）：85-88.

［4］Han JQ.Active disturbance rejection controller and its applications［J］.Control and Decision，1998，13（1）：19-23

［5］Han JQ Active disturbance rejection control technique［C］.Beijing：National Defense Industry Press，2008.

［6］Han Jingqing.From PID to active disturbance rejection control［J］.IEEE Transactionson Industrial Electronics，2009，56（3）：900-906.

［7］黄一，薛文超，赵春哲.自抗扰控制纵横谈［J］.系统科学与数学，2011，31（9）：1111-1129.

［8］Xia Y，Shi P，Liu GP，et al.Active disturbance rejection control for uncertain multivariable system with time delay［J］.IET Control Theory and Applications，2007，1（1）：75-81.

［9］Taloles SE，Kolhe JP，Phadke SB.Extended-stateobserver-based control of flexible-joint system with experimental validation［J］.IEEE transactions on Insustrial Electronics，2010，57（4）：1411-1419.

［10］Gao ZZ.Scaling and band-parameterization based controller tuning［C］.Proceedings of the American Control Conference，2003：4989-4996.

［11］高志强.浅谈工程控制的信息问题［J］.系统科学与数学，2016，36（7）：908-923.