让解题思路因联想而“自然”*
——一道高考题的解法探究与拓展
●
(浙江师范大学数理与信息工程学院,浙江 金华 321004)
例1设x,y为实数,若4x2+y2+xy=1,则2x+y的最大值是______.
(2011年浙江省数学高考理科试题第16题)
本题作为数学高考填空题的压轴题,难度较大,许多学生面对此题时一筹莫展,无从下手.其实此题较为开放,入口较宽,是一道精心打造的好题.此题命题者是如何求解的笔者无从得知,以下是网上及众多数学教辅资料上提供的一种解法:
解法1由4x2+y2+xy=1,得
则
当且仅当2x=y时,等号成立,即

上述解法非常简洁,但是技巧性太强.第一步“配方”的过程尤如“神来之笔”,如同波利亚所谓的“从帽子里跑出一只兔子”,学生除了赞叹方法的巧妙之外,只能望题兴叹:我怎么就想不到?[1]出现这种状况的主要原因是:上述解法的解题思路不“自然”.
那么,如何才能形成“自然”的解题思路呢?在面对一个较困难的问题时,波利亚在《怎样解题》一书中,他给学生的建议是:通过联想,找到一个你所熟悉的与现在的问题具有相同或相似未知数的问题,分析差异,然后利用你已有的活动经验对你现在的问题加以解决[2].
下面以上述试题的求解为例,就如何才能形成“自然”的解题思路作一些探讨.
1 解法探究
联想1已知条件4x2+y2+xy=1的左式是一个二次三项式,对于这种二次三项式,常用方法是试图将其配方,使其出现平方和的形式,然后采用三角换元.
解法2由4x2+y2+xy=1,配方得

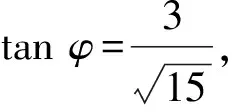

联想2将已知条件写成
(2x+y)2=1+3xy,
联想到基本不等式
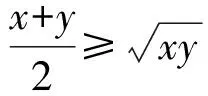
可将其转化为关于2x+y的不等式,求解后即得2x+y的最大值.
解法3由4x2+y2+xy=1,得
(2x+y)2=1+3y.

所以
即

联想3将已知条件写成
由左边的形式可以联想到余弦定理,从而可以将2x,y,1放入一个三角形中.

由正弦定理知
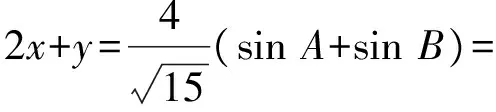
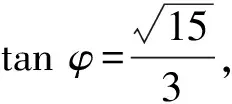

联想4题目要求的是2x+y的最大值,这是一个二元一次函数的最值问题,联想到我们常利用数形结合思想处理二元一次函数的最值问题.可将4x2+y2+xy=1视为一封闭的二次曲线,记2x+y=t,视为一动直线,目标函数t=2x+y的最值往往产生于直线与曲线相切这一极端位置.
解法5设2x+y=t,联立
消去y,得
6x2-3tx+t2-1=0.
由于直线与曲线有公共点,则
Δ=(-3t)2-4×6(t2-1)≥0,
化简得
从而

2 试题拓展
将已知条件4x2+y2+xy=1中的常量“1”用变量“z”替换,上述试题可拓展为:
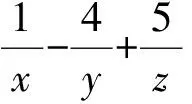
本题的难度虽然很大,但是联想到例1的多种解法,我们不难得出本题的多种解法,有兴趣的读者不妨一试,以下提供其中的一种解法:
解由4x2+y2+xy=z配方得
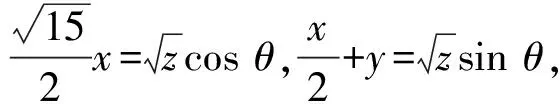
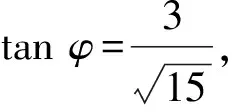

设x=t(其中t≠0),则
y=2t,z=4t2+(2t)2+2t2=10t2,

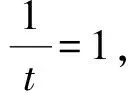
在进行解题教学时,教师应淡化解题技巧,注重通性通法;应多引导学生去“联想”,力争贴近学生思维的“最近发展区”,让解题思路因联想而“自然”,从而让学生感到这种解法便是“他应当想到的”,进而有效提升学生的解题能力.在此基础上,教师若能对已解决的问题进行适当的拓展,则更能有效提升学生的解题能力.
[1] 波利亚.数学的发现[M].刘景麟,曹之江,译.北京:科学出版社,2006.
[2] 波利亚.怎样解题[M].阎育苏,译.北京:科学出版社,1982.
[3] 孔胜涛.编题教学法在数学教学中的尝试[J].数学教学研究,2017(7):23-25.

