关于提高数学课堂教学有效性的三项“修炼”*
●
(杭州第四中学,浙江 杭州 310018)
课堂教学的有效与高效是一线教师永恒的话题.在新课改如火如荼进行、数学核心素养的培养成为数学课堂教学终极目标的今天,如何让数学课具有高质量和高品位,真正实现新一轮课改的初衷,切实做到高质轻负,应该是我们每一个数学教育工作者必须直面和思考的问题.以笔者多年教学的体会,以下三项“修炼”最为关键.
1 深钻教材,寻求对教材内容的全新理解
教学过程需要精心设计,而设计就必须透彻理解教材.这如同艺术创作:一个编剧,在将原著改编成剧本时,如果缺乏对原作的悉心研读和大胆创作,编不出好剧本;一个导演,若没有对剧本和原作的深透理解,没有把握住原著和剧作家们的创作意图,则导不出催人泪下的艺术作品;一个演员,若不能吃透原作和剧本,对自己所扮演的角色缺乏全新的理解和感受,对作品所反映的时代背景缺乏必要的了解,则无法把握住人物的个性特征,也就难以真正进入角色,自然塑造不出有血有肉的感人艺术形象.教师的教学亦要编、要导、要表演,且均要由教师一手完成,这就要求教师充分发挥对教材的编导作用,钻研教材,驾驭教材,处理教材,开掘教材,把数学知识的学术形态变为教育形态,并在此基础上为实施教学活动提供高质量的教学“剧本”.
因此,当今的数学教师要养成这样一种习惯:要潜心钻研,寻找新感觉;悉心挖掘,进行再创造.要真正深入到教材之中,不厌其烦地精读教材,思人所未思,见人所未见,从教的角度,设法寻找一种全新感觉、一种对数学内容本质的认识:教材中蕴含了哪些重要的数学思想;构成了什么样的知识结构与体系;本节内容在一章、一个模块甚至在整个高中数学中处于怎样的地位;涉及到哪些类型的数学问题;牵扯到哪些过去的知识;这个知识点的本质是什么;通俗的解释该是怎样的……在此基础上,做到概念有自己的理解,公式定理有自己的阐释,数学思想有自己的说法与解释,解题思路有自己独到的透彻分析与总结,能从字里行间理出知识的基本脉络,找出重点,理出难点,抓住关键点,从抽象、枯燥的数学知识中捕捉其丰富生动的内涵,从“看不见的战线”上挖掘、提炼出鲜为人知的数学思想方法,把书由薄读厚,再由厚读薄,然后内化为自己的理解,在讲台上旁征博引,纵横驰骋,引导学生的思维自然地流淌.
1.1 从宏观上梳理出每一板块的知识框架
平面解析几何作为用代数方法研究几何问题的一门学科,知识容量之大、解决问题之多、涉及问题之广、方法技巧之妙、运算能力要求之高是数学其他内容所无法比拟的.在总复习时,有时感到头绪很乱,然而只要深入研究,悉心揣摸,就不难发现:是基本概念(曲线与方程)、基本原理(数形结合)、基本思想(运动变化的辩证思想)、基本方法(坐标法:用代数方法研究几何问题)、基本联系(外在联系即解析几何与三角、代数、平面几何的联系;内在联系即点与实数对、曲线与方程等)这“五个基本”支撑起解析几何这座“大厦”.
“五个基本”搭起了解析几何知识的总体框架,让高考总复习站到了应有的高度,为学生勾勒出了一个明晰的知识网络图,每一单元,不论是直线与圆,还是圆锥曲线,都按照这一框架展开复习与探究,有效地帮助学生完成了对这部分内容的知识构建.
1.2 从微观上给出抽象概念的生动解释
数列极限教学中,“极限的本质究竟是什么;‘ε-N定义’中为什么要引入任意小的正数;为什么要求当n>N时必须有|an-A|<ε成立”……对这些问题,教师必须有自己的深透理解与感悟:极限实质上反映一个无穷数列的变化趋势、极限值(如果存在),实际上就是一个无穷数列无限变化后的最终归宿点,是“后面”的项要逐步逼近的“目标”,是这个数列“将来”要到达的“目的地”.要保证an变到A那里去,就必须要求后面的项an与A十分接近.那么,怎样才能保证越来越接近呢?只要|an-A|越来越小即可.怎样才能让|an-A|越来越小呢?不能说空话,必须给出定量说明.这就犹如写作文时要描述天气的寒冷与夜色的漆黑时,如果仅仅用“很冷”与“非常黑”分别表述不能令人信服,但如果用“滴水成冰”“呵气成霜”来描述天气的寒冷,用“伸手不见五指”来描述天色很黑就十分形象,会让人一下子感到天确实很冷,夜色确实很黑.这样解释,学生对概念才能真正理解透彻.
1.3 在解题实践中总结提炼出解题规律
三角恒等式的证明是初学者的一大难点,学生对怎样由一端变到另一端总不得要领.笔者在大量的解题实践中领悟并总结出了“消除差异、追求统一”的三角等式证明八字方针和“化繁为简”“投其所好”“无中生有”“改头换面”“两面夹击”的二十字求证要诀,使学生很快把握住了变形的技巧和策略.
1.4 在深钻细研中追求对数学本质的认识
关于函数奇偶性的教学,教材通过学生熟悉的简单函数图像,让他们发现并感悟部分函数图像关于原点或者关于y轴对称的特点,从而引出函数奇偶性的概念,然后在给出函数奇偶性定义的情况下介绍函数奇偶性的判断、证明及其应用.作为数学教师,如果这个内容的教学就到此为止,那么学生对函数奇偶性这一重要性质的理解将是很肤浅的.事实上,函数奇偶性的实质是反映函数图像的对称性及由此从数上反映出的函数值变化的一种规律——对偶.大多数具有某种对称特性的函数都是因为函数的奇偶性造成的,尽管他们本身可能既不是奇函数也不是偶函数,但平移回去就是奇函数或者偶函数——这样的理解只有仔细钻研教材才能领悟到.在这样的认识下,数学教学产生的效果是学生对数学知识本质的认识,产生的效应是学生对与函数相关的对称性问题的“一揽子”解决,从而自然地形成高效的教学.
因此,对数学教师来说,教材的钻研永远在路上.任何时候,数学教师都必须把对教材的深钻细研放在教学工作的首位.只有对教材的深透理解、对所教内容的潜心挖掘、对数学美的深刻体验、对空间形式与数量关系的深刻认识、对数学知识的重要价值(在生活实践、科技创新、社会发展等方面)真正了解,才能为精当处理教材、把数学内容讲生动、把数学课讲得有趣味奠定基础,连珠妙语才能脱口而出,贴切的范例才能信手拈来,数学教学才能真正做到深入浅出或浅处深入.
2 修炼语言,增强授课的艺术感染力
教学也是一门语言的艺术.记得上大学时,笔者的一位恩师曾谆谆告诫我们:要当好一个老师就必须有“三个一”,即“一口好话,一手好字,一肚子文采”,这“一口好话”其实就是要有好口才要会说,也就是要有较好的语言表达能力.事实上,语言本来就是人们表达感情、交流思想、传递信息的重要工具,当然也是数学教学的重要工具之一.任何一位教师,当他的专业素养和知识总量达到一个关键值后,影响其教学效果的决定性因素就是语言能力.诚如苏霍姆林斯基所言:“教师的语言是什么也代替不了的影响学生心灵的工具,教育教学的艺术首先是语言的艺术.”
因此,从某种意义上说,教师就是一个“卖嘴皮子”的行当,一名拙嘴笨舌的教师,纵然有满腹经纶,也难以成为一个好老师.语言贫乏的老师,课堂上很难提起学生的兴趣,特别是枯燥的数学课,学生不爱听,教学效益自然低下.在课堂上,只有那些能用生动风趣且形象化语言阐释新概念、说明新方法、分析新问题的教师,那些能用浅显通俗的语言去为学生创设出一个个思维情景、能用引人入胜的连珠妙语投石击水般地为学生设置一个个思维场的教师,才能使所讲的课紧扣学生心弦,才能将课堂教学推向一个又一个高潮,才能使每一位学生在美妙的数学语言氛围中轻松自如地掌握知识.这就要求教师必须具备高超的语言艺术,不断加强文学、美学、哲学修养,收集俗语,积累词汇,训练口形,训练出一张能说会道的嘴来,能讲出一口字正腔圆、感染力强的话来,以动听优美的课堂语言将自己所传授的数学知识染上浓郁的艺术色彩,使数学成为鲜活的东西,变成一首感人的诗、一副优美的画、一曲动人的歌.
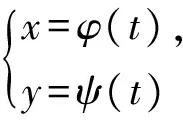
与二项式有关的系数问题中,求系数的最值是颇有难度的一种题型.如何引导学生快速找到解题的突破口?笔者设计了如下语言启发诱导:由于要找的系数要最大,那么看了这一项系数,再看别的项的系数,就会有一种“会当临绝顶,一览众山小”的感觉.一句脍炙人口的唐诗,蓬荜生辉,学生豁然开朗.
复合函数f[g(x)]单调性的判断中,除定义法外,有时用“心”推理更能快速见效.为此,笔者又借用了一句当时十分流行的歌词——“跟着感觉走”,学生在会意的微笑中轻松地掌握了判断复合函数单调性的诀窍.
三角函数图像的作法教学往往平淡无奇,不易掀起教学高潮.笔者组织了这样一段语言加以渲染:正弦、余弦函数作出的正、余弦曲线就如同从一个宝葫芦中释放出来的滚滚波涛,而正切曲线则犹如飞流直下的庐山瀑布,真是美妙无比.抽象的函数曲线被染上了浓郁的文学色彩,充满了诗情画意,学生在一种美的享受中掌握了所学知识.
此外,教师讲课的激情、语调、表情等均会影响授课的效果.我们应当博采众长,兼收并蓄,认真学习、模仿演说家的气质与风度,用饱满的激情、用全身心的投入、用自己对所教数学学科美的感受去影响和打动学生,在学生面前留下绘声绘色的讲台形象,使每一节课都能变为引起学生心灵共鸣的演讲,从而调动学生学数学的浓厚兴趣,使他们对数学课百听不厌,每天盼望着上数学课.
3 在学习和研究状态下教学,做到知识和教学方法上的“长流水”与“自来水”
要给学生一杯水,教师首先要有“一桶水”,这曾经是教育对教师素质的起码要求.现在看来,这个要求未免有点太低.因为作为知识传播者的教师,始终在进行着创作性的劳动,仅靠知识的原始积累,仅靠原有的“一桶水”,是无法适应现代教育发展要求的.因为这“一桶水”如不及时添加,舀着舀着就会枯竭,如果不及时更换,时间一长还会“变味”,一些名师教学艺术长青的秘诀就在于不满足现有的“一桶水”,而是设法做到知识与教学方法上的“长流水”与“自来水”,让自己始终拥有一桶新鲜的“活水”.
这里的“长流水”,就是说教师要多些“书卷气”,不断学习,不断更新,不断充电,不断积累,从各种渠道获取教育教学营养,教到老,学到老.“问渠哪得清如许,为由源头活水来”,只有及时用新理论、新观点、新知识武装头脑,把时代的“新鲜活水”引进自己的课堂,用新的理念、新的思想指导教学,才能常教常新.因此,为了让自己的教学艺术长青,为了保证一辈子上好课,首先要学习学习再学习:学教育教学理论、翻专业书刊、借鉴他人优秀的教学经验.力求使自己始终在最新教育教学理论的引领下,站在新课程教育的制高点上,居高临下地审视教学,驾轻就熟地处理教材,灵活精当地选择教法,游刃有余地进行课堂教学,使讲课做到高屋建瓴、活水涌流,在学生面前展现出一个清新、明朗、开阔的数学知识天地,进而诱发学生产生不可遏止的求知欲,对学习数学乐此不疲.
这里的“自来水”是指教师应该把自己当做一名学者,在教学的同时搞教研,做学问,拿出自己的理解,走出自己的路子,教出自己的特色,使出自己的绝活,在研究状态下逐步形成自己的教学风格,使自己感到越教越会教,越教越有新招,随着年龄的增大虽然“徐娘半老”却“风韵犹存”.因此,要强化教研意识,以研促教,做一个教学上的有心人.教研不是名人的专利,人人都可以搞.作为常年默默无闻耕耘在三尺讲台上的教师,谁没有泪水滚滚的时候,谁没有独具匠心的得意之作?教法上的灵感、教材上的发现、教课过程中的困惑、想法比比皆是,如果不及时总结,把那些为之付出了汗水的思考和成功经验记录下来,那么就会如同过雨烟云,随着岁月的流逝因时过境迁而烟消云散,白白浪费掉一笔十分宝贵的教学财富.相反,倘若每位教师都能当教学上的有心人,及时捕捉教学灵感,把那些一闪即逝的新想法、新做法、新困惑、新疑虑随时记下来,前后加以联系、整理思索,则会悟出许多道理,某个课题或者成果雏形就可能会应运而生.如果再加以总结、提炼,并上升到理论高度写出来,那么恐怕就是一篇颇有见地的教育教学论文,倘若将这些研究成果再用于自己的教育教学实践,则教学就会上升到更高的层次,今年上过的课明年再去上,就会有一种“岁岁年年人不同”之感,教学效果较以往不言而喻.
当然,就教师层面来说,影响数学教学有效与高效的因素还非常多,诸如教师的专业功底、教师的人格魅力、教师的品德修养、教师的教学理念、教师对多媒体技术的熟练运用、教师独特的数学教学方法等.但“钻研教材理解数学”“修炼口才丰富语言”“在教中研、在研中教”应该是当今数学教师首先要做的三项“修炼”,只有对教材内容理解深入才能把抽象的数学知识讲清楚、说明白、讲透彻,才能让学生感到数学浅显好懂;拥有出色的口才则能最大限度地调动学生学习数学的热情,让学生感到数学生动、有趣、好玩,枯燥乏味的数学才能妙趣横生,神奇的数学方法才能变得精妙;教师在研究状态下进行的数学教学才更贴近学生的实际、更切中时代的脉搏,让我们的预设产生最大限度的生成,更能让我们数学教师在“照亮别人的同时也完善了自身”,进而不断享受到创造性教学的乐趣,何乐而不为呢?

