解题教学需要重视发展学生的联想能力*
●
(南京师范大学附属扬子中学,江苏 南京 210048)
联想是新旧事物建立联系的产物,是形象思维,是一种记忆方法和思维方法,数学解题的思路寻求应该基于已有的认知结构进行思维方法联想[1].在平时的解题教学中,笔者经常会遇到这样的现象:学生面对新的问题时感觉雾里看花而无从下手,等到教师评讲完才恍然大悟.学生的困境不单单是接受能力差导致数学成绩不理想,原因当然众多,其中最突出的就是解题时缺乏联想能力,不会将新问题与已掌握的知识或旧问题联系起来.因此,在解题教学中,发展学生的联想能力,增强学生对数学解题的灵活性是十分必要的.以下笔者结合2017年江苏省数学高考题,从联想概念和原理、联想通性通法、联想基本数学思想、联想解题基本流程这4个方面,谈谈解题教学中发展学生联想能力的重要性,以期提升学生的解题能力.
1 联想概念、原理
章建跃博士认为:“在解题教学中,要使学生逐步养成从基本概念、基本原理及其联系性出发思考和解决问题的习惯.”其实学生眼里的粗心错误大都是对知识或概念的联想不准确、不到位造成的.因此,基本概念、原理的重要性不言而喻.基本概念、原理是学生解题时产生联想的基础,准确联想出正确的概念和原理是善于解题的前提.
在解题教学中,教师应该在概念复习上下功夫,要打通、串联起概念在整个章节、甚至整个阶段学习中的关系、地位与作用,在解题的过程中不断突出联想概念、原理等解题的规律与方法.函数是高中数学最重要的概念,函数的下位概念中,最重要的是函数的单调性、奇偶性,研究函数问题的实质就是研究函数的图像和性质,解决函数问题,只要能准确联想出函数的图像与性质,问题就会迎刃而解.

(2017年江苏省数学高考试题第11题)
解函数f(x)的定义域为R,因为
所以函数f(x)为奇函数.又
且f′(x)=0不恒成立,从而f(x)在定义域R上单调递增,于是
f(a-1)+f(2a2)≤0,
等价于
f(a-1)≤-f(2a2)=f(-2a2),
即
a-1≤-2a2,
得
评注本题是以单调性、奇偶性概念为载体的函数不等式问题,如果直接求解,计算相当繁琐;但如果能够积极联想函数单调性、奇偶性等概念,是不难得到答案的.奇怪的是,从笔者平时对学生的观察和阅卷得分来看,这类题得分率都不高,主要原因是学生缺乏联想以及运用概念、原理解题的意识,应当引起重视.
2 联想通性通法
章建跃博士认为:“注重通性通法才是好数学教学.”数学难学,难在何处?除了数学概念本身外,看似千变万化的解题方法或许是主因.不少教师的解题教学,热衷于解法1、解法2、解法3……,却摒弃了大巧若拙的通性通法,把学生的注意力引到了“题型+技巧”上,使学生忘掉了解题的根本,没有真正学会最基本的数学思考方法;注重通性通法是高考命题一直坚持的原则[2].在解题教学中,让学生掌握最基本的方法,强调方法的普遍性,培养学生联想通性通法的意识,让学生具有一双透过现象看本质的“慧眼”,这才是追求解题教学的“长远利益”.

图1
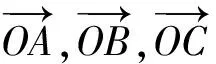
(2017年江苏省数学高考试题第12题)
解法1(基底法)由题意得


又由tanα=7,其中α∈[0,π],得

得
两式相加得
m+n=3.

即
得
m+n=3.
评注本题考查的是高考要求的8个C级考点之一:平面向量的数量积.基底法、坐标法及定义法是处理平面向量数量积的通用方法,只要学生能够积极联想出3种通法的其中一种,是不难得到答案的.
3 联想基本数学思想
方法是技巧的积累,思想是方法的升华,解决数学问题的灵魂就是思想;学数学知识需要数学思想,学数学解题更需要数学思想给力.解题教学就要发挥数学思想的功能,在解题教学中,积极引导学生联想高屋建瓴的数学思想,让学生站在较高的观点上去研究解题,从数学的本质上去看待解题,学生的思维能力就能得到充分的发展,数学问题的解决就变得简单而自然[3].解题时常用的数学思想有:函数思想、转化思想、数形结合思想和分类讨论思想等等.

(2017年江苏省数学高考试题第14题)
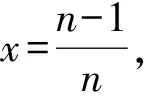
从而
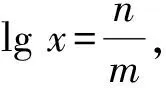
矛盾,故lgx∉Q,画出函数图像(如图2).
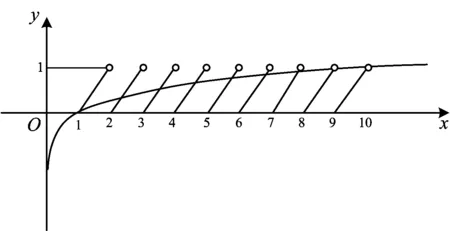
图2
除(1,0)外,其他交点的横坐标均为无理数,每个周期x∉D的部分,且在x=1附近仅有一个交点,因此方程f(x)-lgx=0的解的个数是8.
评注这是一道函数零点问题.判断函数零点个数的常用的思想方法有:1)解方程;2)零点存在性定理,函数思想;3)数形结合思想,转化为两个函数图像的交点个数.其中第3种是解决这类问题的利器.

图3
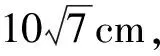
1)略;
2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
(2017年江苏省数学高考试题第18题)
解1)略.

图4
2)如图4,以EG所在直线为x轴、OO1所在的直线为y轴建立直角坐标系,则E(-7,0),G(7,0),水面所在的直线为y=12.记∠EGG1=α,∠ENG=β,则
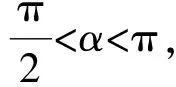
从而直线GG1的方程为
3y-4x+28=0.
在△ENG中,由正弦定理可得

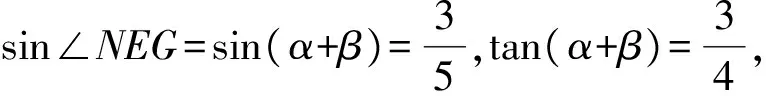
从而直线EN的方程为
4y-3x-21=0.
记EN与y=12的交点为P2,可解得P2(9,12),过点P2作P2Q2⊥EG,垂足为Q2,则
P2Q2=12,EQ2=16,
从而
EP2=20.
评注本题是以几何图形为载体的应用题,其实质是解三角形问题.第2)小题的难点是复杂的边角关系,不容易直接求出线段长度,使得不少学生走了弯路.此题的本质就是求一个变量的值,有两种思路:一是函数的思想,直接求出变量的值;二是方程的思想,寻找该变量满足的方程或等式.若引入了多元变量,则消元思想将是不错的选择,最终回归到转化与化归的基本数学思想.只要学生有联想转化、函数与方程等数学思想的意识,这道题就很容易得分.
4 联想解题基本流程
波利亚发明了《怎样解题》表,提出了“弄清问题、拟定计划、实现计划和回顾”这4个思维流程,4个流程的关键是弄清问题,核心是拟定计划,实现计划,提高在于回顾反思.当学生有了一定的联想习惯后,对于一些简单的数学问题,可能会很容易解决,但当遇到有一定难度的问题时,仍无法独立完成,这就需要教师积极引导学生联想解题的4个基本流程.弄清问题就是说,在解题之前,将题目中的已知条件、潜在条件及要求问题理清,找出它们的来龙去脉.解题前问问自己:从已知条件还能知道什么,结论需要什么?拟定计划就是在弄清问题的基础上,探索已知、可知与结论之间的桥梁.如果弄不清已知和结论的联系,那么试着循着已知往前走一走.实现计划不仅能便于发现思路可能存在的问题和错误,也可以尽可能地做到规范书写解答,会而不丢分;回顾、反思、升华自己对解法的理解,尽可能地提炼总结出处理“一类问题”的经验与方法.
解题教学的最终目的是让学生学会解题.实践表明:积极联想、运用解决问题的基本流程,无论是成功的还是失败的尝试,对提高解题能力和思维能力有着重要的积极作用.
例5对于给定的正整数k,若数列{an}满足an-k+an-k+1+…+an-1+an+1+…+an+k-1+an+k=2kan对任意正整数n(其中n>k)总成立,则称数列{an}是“P(k)数列”.
1)略;
2)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
(2017年江苏省数学高考试题第19题)
分析1)略.
2)(弄清问题) 因为数列{an}既是“P(2)数列”,又是“P(3)数列”, 所以
an-2+an-1+an+1+an+2=4an(其中n>3),
(1)
an-3+an-2+an-1+an+1+an+2+an+3=6an(其中n≥4).
(2)
(拟定计划)结论的实质是利用等差数列定义证明an+1-an=d(其中d为常数)或2an=an-1+an+1.由已知推结论,需要减元.
方法1式(2)-式(1),可得
an-3+an+3=2an(其中n≥4).
接下来通过赋值法证明3个子等差数列公差相同且前3项等差即可.
方法2由式(1)知
an-3+an-2=4an-1-(an+an+1),
(3)
an+2+an+3=4an+1-(an+an-1),
(4)
将式(3)、式(4)代入式(2)可得
2an=an-1+an+1(其中n≥4).
接下来通过赋值法证明前3项等差即可.
(实现计划)规范书写省略.
(回顾反思)新定义题目,首先是翻译定义,由递推关系得变量之间的关系,利用减元、赋特殊值等思想回归等差数列的定义.
评注这道用新定义形式命题的数列压轴题,考查的是等差数列证明.教师要在解题教学中帮助学生养成良好的解题习惯,有意识地去引导学生用流程化的思维去联想“一类问题”的解题基本流程.
5 结束语
总之,在解题教学中,通过对学生联想能力的培养,不仅能使学生形成良好的认知结构,还能使学生建立知识网络,掌握数学知识内在的联系,抓住数学思维的内在本质,加深数学思想方法的理解,引领学生跳出题海.只有重视发展学生在数学解题中的联想能力,才能使学生真正领悟数学真谛,懂得数学价值,学会数学地思维,把知识的学习、核心素养的培养与发展智力有机地统一起来.
[1] 张朋举.基于方法联想的高三解题教学实录与反思[J].中小学数学:高中,2017(5):47-49.
[2] 曹凤山.绿色的解题策略:回归原点[J].中小学数学:高中,2016(10): 43-45.
[3] 章林海.揭示本质,找准突破,让思维回归“自然”[J].中学教研(数学),2017(5):4-8.

