探索思考 永无止境*

●

(蛟川书院，浙江 宁波 315200)

近日，笔者在解读《浙江省宁波市2016年初中毕业生学业考试说明》时，遇到了一道求线段最值的题目，许多师生都无从下手.现将原题呈现如下：

图1 图2

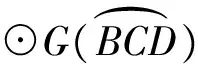
∠H=∠ACB=∠EDB,

而

∠H=∠DGO,

从而

∠EDB=∠DGO.

又

∠DGO+∠BDG=90°,

得

∠EDB+∠BDG=90°,

即

∠ODG=90°,

于是

即

做完此题后笔者很是激动，这么难的一道题目在一步步地思考中被解决.但同时也引发了笔者深刻的思考，求线段的最值问题是近几年宁波市中考考纲中的重要题型之一，也是各地中考试卷中一道亮丽的风景.解决此类问题的关键是要结合题意，借助相关的概念及图形的性质，将最值问题转化为相应的数学模型，这些数学模型主要包括将最值问题转化为点到直线的距离，利用垂线段最短解决，还可以转化为点到圆上一点的最大值与最小值模型解决，但是对于学生而言难度最大的是如何确定点的运动路径，找不到运动路径根本无法谈解题策略.如果按照上述的解题思路来解决问题，几乎所有的学生都做不到，也就是说这个题目的得分率将会非常低，那么这样的题目放在考试中又有何意义呢？无独有偶，在中考模拟试卷中笔者又遇到了一个类似的问题：

例2如图3，⊙O半径为4，Rt△ABC的顶点A,B在⊙O上，∠B=90°，AB=BC,点C在⊙O内，当点A在圆上运动时，OC的最小值是______．

图3 图4 图5

这样将线段OC进行转化，比一开始就找动点的运动路径简单得多，由此笔者对例2进行了深入探究，又得到了如下模型：

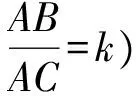
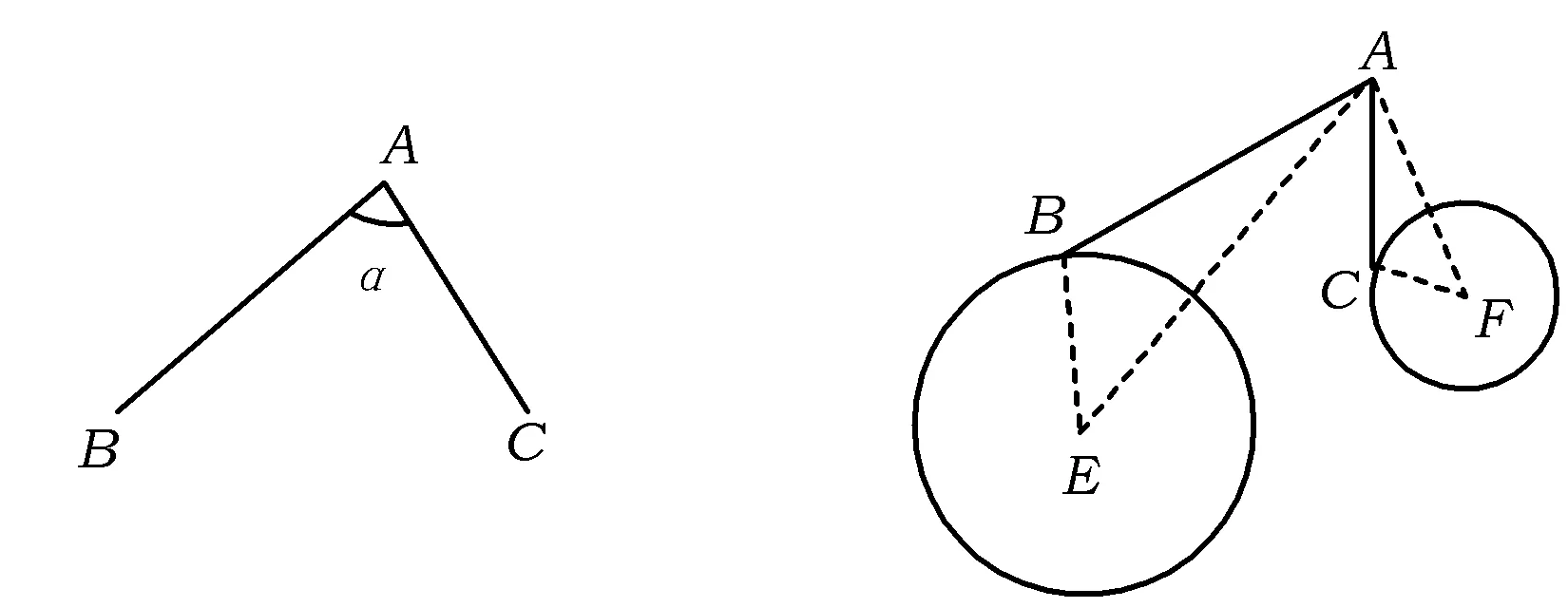
图6 图7

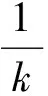
图8

做到这里，收获甚大，这样的一个题目从开始的迷茫到越做越精彩，还得到一个基本模型，并且能应用到以后的求最值问题中，让隐性的思想方法浮出水面，从懵懂到熟悉到内化，从自觉提炼到自觉综合运用，使思维逐步深入和提升.笔者相信这也是数学能让广大的教师、学生去探究它的魅力所在，刚开始的愚钝并不可怕，可怕的是没有继续进行探究的信念，相信只要我们敢于探索，就会越走越精彩.这种思考、这种探索应当融入到我们的教学生活中，学需思辨，保持朴素，富有生命力……唯有如此，教师才能收获持久而深入的专业发展，学生才能收获有效而智慧的学习态度.