悬臂式蜂窝夹层板的非线性动力学建模及分析*

岐晓辉 张君华 张伟

(1.北京信息科技大学机电工程学院, 北京 100124) (2.北京工业大学机电学院, 北京 100124)

引言

蜂窝夹层结构具有重量轻、高比刚度和高比强度以及良好的结构稳定性和能量吸收性等优越的性能,因而广泛应用于现代工业制造的各个方面.在航空航天工业中,蜂窝夹层结构大量用于飞机的机翼、雷达罩、机舱、尾翼、升降舵和储物箱等部位.蜂窝芯夹层板由较薄的上下蒙皮和较厚中间芯层组成.它的芯层是由金属材料、纸质材料或者其它材料制成的六边形孔格,蒙皮在芯层的上下两面胶结或焊接.蜂窝夹层板的结构如图1所示.

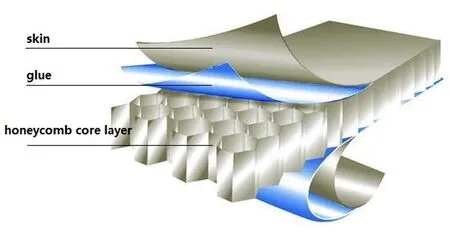
图1 蜂窝夹板结构示意图Fig. 1 Structure of honeycomb sandwich plate

蜂窝芯层等效是蜂窝夹层结构相关研究的前提和基础.1969年,Allen[1]针对蜂窝芯层等效提出了一种忽略芯层面内刚度和弯曲刚度的假设,认为芯层仅能抵抗横向剪切力,极大地简化了受力分析,这种假设在早期的工程中应用非常广泛.1982年,Gibson[2]等对采用欧拉伯努利梁理论,利用材料力学公式推导出等壁厚正六角形蜂窝芯层的二维等效弹性参数公式.1999年,富明慧[3]等考虑蜂窝壁版的伸缩变形对面内刚度的影响,提出了一种考虑蜂窝芯层面内刚度的简化方案,克服了Gibson公式的缺陷.2001年,Kim[4]等开发了一个非均匀支撑的柱状结构的常规三维各向异性模型,通过该模型来研究二维六角形、三维六角形和菱形蜂窝材料柱状结构的力学特性.2008年,祝涛[5]等考虑面内载荷对蜂窝芯层等效弹性模量的影响,拟合了非线性等效弹性参数.同年,孙德强[6]等将铝制蜂窝孔壁视为纤细梁,在考虑弯曲和伸缩变形的基础上利用Timoshenko梁理论处理蜂窝孔壁的剪切变形,推导出了与有限元结果更加接近的双壁厚一般六角形蜂窝芯层的面内等效弹性参数公式.2011年,陈玳珩[7]等提出了蜂窝芯层和蒙皮在位移连续性条件下的等效弹性模量的理论分析的新的计算方法,并与有限元数值分析相比较验证其准确性.2012年,陈梦成[8]等提出了以蜂窝芯正六角形胞元壁板弯曲和扭转为基础的蜂窝夹层板的计算方法.2015年,富明慧[9]等基于Timoshenko梁理论,利用文献[6]的计算方法,推导出了一般六角形等壁厚蜂窝芯的面内等效弹性参数公式.

2013年,Motley[10]等研究了全部和部分浸没的悬臂复合板的边界条件对自由振动响应的影响以及这些影响是如何根据材料属性而变化的.同年,Hao[11]等研究了热环境下受到横向和静态面内预加激励的功能梯度悬臂圆柱壳的非线性动力学行为.同年,杜长城[12]等采用Galerkin法和平均法研究了四边简支条件下仅受到横向简谐激励作用的功能梯度薄壁板的非线性动力学响应.同年,Wang[13]等研究了热环境下置于弹性地基上的具有功能梯度表层的复合板的非线性动力学响应.2014年,Zhang[14]等研究了同时受到横向激励和面内激励作用的简支边界条件下,空间构架点阵夹芯层合板的非线性动力学响应.同年,Zhang[15]等研究了横向气动载荷和参数激励联合作用下复合材料悬臂外伸矩形板在伸出过程中的非线性动力学问题.2015年,Ta[16]等利用改进板理论分析了置于弹性基地上的功能梯度板的动力学响应.2016年,Azarboni[17]等研究了非理想矩形板在六种边界条件下激励频率对非线性动态脉冲屈曲的影响.同年,Parandvar[18]等使用有限元方法研究了受到热和谐波负载下功能梯度扁壳的非线性动力学响应.

综上所述,国内外很多学者对不同边界条件下蜂窝夹层板的非线性动力学特性进行了大量研究,但对于复杂载荷作用下悬臂式蜂窝夹层板的非线性动力学响应的研究相对较少.另外,多数文献在蜂窝芯层等效时采用了文献[2]给出的Gibson公式,本文采用了更加接近有限元实体单元的等效弹性参数公式对蜂窝芯层进行等效简化,以悬臂式矩形蜂窝夹层板为研究对象,考虑面内激励和横向外激励的联合作用以及阻尼等对系统的影响,基于Reddy高阶剪切变形理论,应用Hamilton原理建立悬臂蜂窝板的动力学控制方程.利用Galerkin方法得到该系统的常微分形式的非线性动力学方程,根据工程实际背景选取不同的参数,直接对所得系统进行数值模拟和对比分析.

1 蜂窝夹层板的力学模型

以飞机的机翼振动为实际工程背景,考虑悬臂边界条件下矩形蜂窝芯夹层板,模型如图2所示,矩形蜂窝夹层板的ob边被固定,其余三边自由,x方向边长为a,y方向边长为b,板总厚为H,平面直角坐标系xOy位于蜂窝夹层板的中性面内,z轴竖直向下并垂直于xOy面.假设蜂窝板受到横向的简谐外激励为F=F0cosΩt以及面内简谐激励为P=P0+P1cosΩ1t,并且考虑横向阻尼γ的影响.蜂窝夹层板的上下蒙皮厚度均为hf,正六角形的蜂窝芯层厚度为hc.

图2 悬臂式蜂窝夹层板模型示意图Fig. 2 Model of cantilever honeycomb sandwich plate

由于蜂窝夹层板的蒙皮很薄并且与蜂窝芯层紧密粘结,为了计算方便,我们忽略蒙皮厚度,将蜂窝芯层进行等效简化.一般六角形蜂窝芯层的结构单元结构如图3所示.其中d为蜂窝单元壁板的厚度,h、l分别为蜂窝单元的直壁板和斜壁板长度.

图3 一般六角形蜂窝芯层结构单元Fig. 3 Unit cell of general hexagonal core layer

文献[6,9]推导出的更加接近实体有限元解的等壁厚一般六角形蜂窝芯层的面内等效弹性参数公式为如下形式：

(1a)

(1b)

(1c)

(1d)

其中E1、E2分别为蜂窝芯层在x、y方向上的弹性模量;v12、v21分别为蜂窝芯层在x、y方向上的泊松比;Es为蜂窝芯基体材料的弹性模量,vs为蜂窝芯基体材料本身的泊松比.由于这组公式同时考虑剪切、拉伸和弯曲的影响,并且与实体有限元模型更加接近,因此本文选择公式(1)作为六角形蜂窝夹层板的等效弹性参数公式.

2 臂蜂窝夹层板的动力学方程

根据Reddy的三阶剪切变形理论,蜂窝夹层板的位移场可以写为如下形式[19]:

u(x,y,z,t)=u0(x,y,t)+zφx(x,y,t)-

(2a)

v(x,y,z,t)=v0(x,y,t)+zφy(x,y,t)-

(2b)

w(x,y,z,t)=w0(x,y,t)

(2c)

其中u0、v0、w0为板中性面在x、y、z方向的位移,φx、φy分别为中性面的法线对于x、y轴的转角,h为板的厚度.

非线性应变位移关系如下:

(3)

将(3)式代入(2)式可以得到位移形式的应变表达式为如下(4)式:

(4)

上式中:

(5)

根据Hamilton原理建立蜂窝夹层板的非线性动力学方程为如下形式:

(6a)

(6b)

(6c)

(6d)

(6e)

其中应力的合力与应变的关系表示为如下形式:

(7a)

(7b)

(7c)

(7d)

(7e)

上式中:

(Aij,Bij,Dij,Eij,Fij,Hij)=

(Aij,Dij,Fij)=

悬臂式蜂窝夹层板的边界条件为：

x=0:w=v=u=φx=φy=0

(8a)

(8b)

(8c)

(8d)

(8e)

其中等效剪力可以表达为:

取横向位移w的模态函数为如下形式:

w0=w1(t)X1(x)Y1(y)+w2(t)X2(x)Y1(y)

(9)

其中:

Xi(x)=sinλix-sinhλix+αi(coshλix-cosλix)

Yj(y)=sinμjy+sinhμjy-βj(coshμjy+cosμjy)

cosλiacoshλia+1=0, cosμjbcoshμjb-1=0

悬臂式蜂窝夹层板的主要振动形式为横向振动,因此很多文献在研究悬臂边界条件下板的振动时仅考虑它的横向位移,本文为了更加准确地描述蜂窝夹层板的非线性振动,综合考虑面内振动和横向振动,引入其他方向的模态函数为如下形式：

(10a)

(10b)

(10d)

(10d)

设横向激励的表达式为如下形式:

F0(t)=F1(t)X1(x)Y1(y)+F2(t)X2(x)Y1(y)

(11)

根据Galerkin法,将所有模态函数式(9)、(10)以及(11)式分别代入相应的偏微分方程(6a)～(6e),然后在等式的两边乘以相应的模态函数部分并在整个板内积分,并忽略u,v,φx,φy方向的惯性项,可以得到悬臂边界条件下蜂窝夹层板的两自由度非线性动力学常微分方程为如下形式:

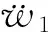
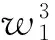
(12a)

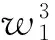
(12b)

3 数值模拟

本节利用Runge-Kutta方法直接对悬臂式蜂窝夹层板的两自由度非线性动力学方程(12)进行数值模拟,分析激励和阻尼对系统非线性振动的影响.铝合金矩形蜂窝夹层板的长a=5m,宽b=2m,蜂窝芯层厚度hc=0.01m,材料基体的泊松比vs=0.33,芯层基体密度和弹性模量分别为ρs=2.66×103kg/m3和Es=72×109Pa,正六角形芯层壁板厚度和边长分别为d=0.0008m和l=0.01m.横向激励和面内激励的频率为Ω=Ω1=100Hz,阻尼为γ=150N·s/m,经计算得方程(12)中各系数取如下值：a1=6.99×109,a2=-3.36×1010,a3=4.88×1010,a4=-1.50×1010,a5=-120.09,a6=-3161.98,a7=-0.41,a8=-0.41,a9=0.93,b1=1.87×108,b2=1.14×1010,b3=-2.23×1010,b4=1.09×1010,b5=731.85,b6=-4948.91,b7=-0.41,b8=-0.41,b9=0.93.

当横向激励为F1=27Pa和F2=15Pa,面内激励为P0=11Pa和P1=8Pa,系统出现周期运动如图4所示.

当横向激励为F1=25Pa和F2=10Pa,面内激励为P0=25Pa和P1=12Pa,系统出现3倍周期运动如图5所示.

保持横向激励为F1=25Pa和F2=10Pa,减小面内激励为P0=11Pa和P1=8Pa,系统出现概周期运动如图6所示.

在保持面内激励为P0=11.2Pa和P1=4.2Pa的同时,减小横向激励为F1=-4.9Pa和F2=1.5Pa时,系统出现混沌运动如图7所示.

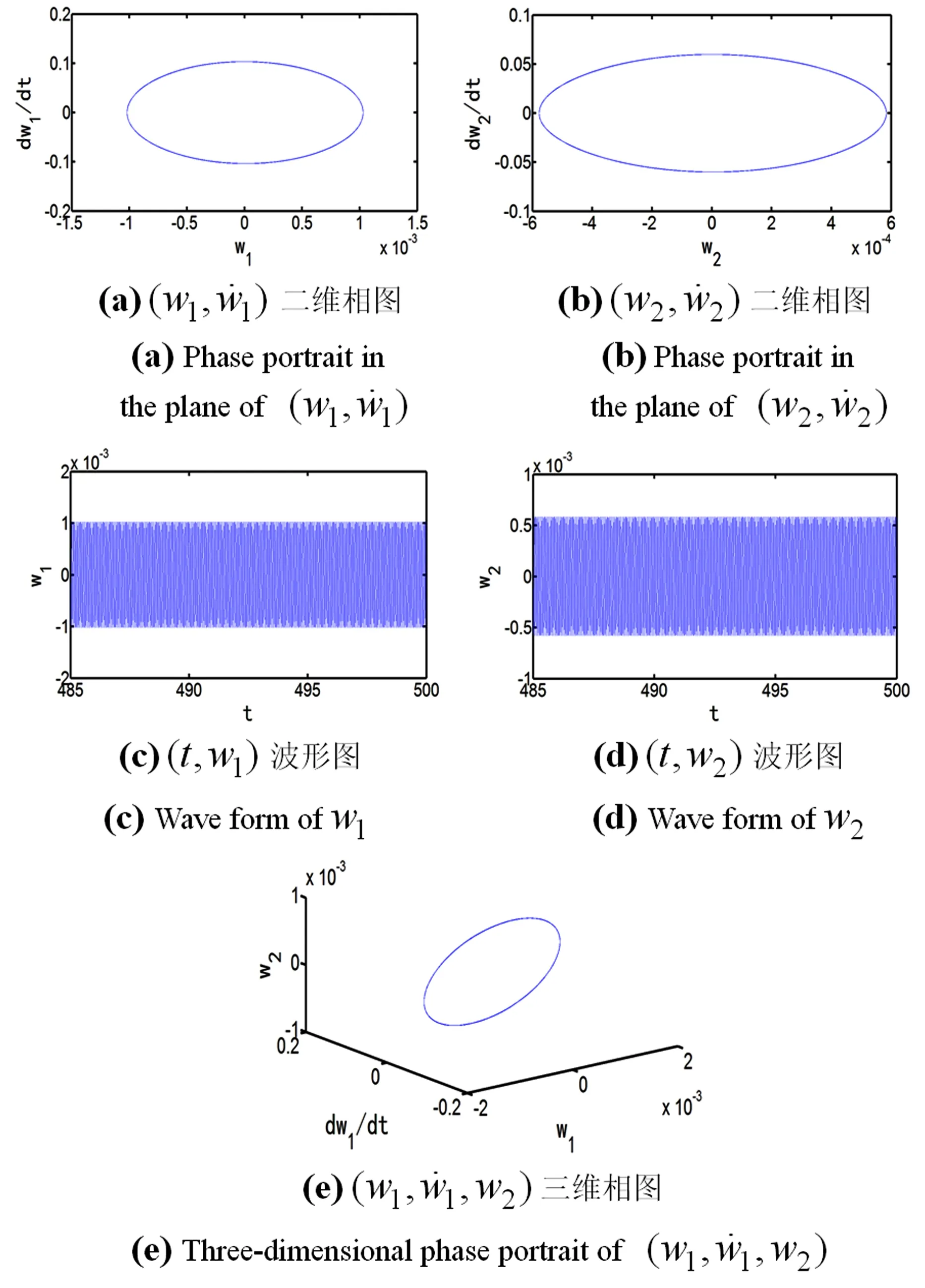
图4 周期运动Fig. 4 Periodic motion of the cantilever honeycomb sandwich plate

图5 3倍周期运动Fig. 5 Three-periodic motion of the cantilever honeycomb sandwich plate

图6 概周期运动Fig. 6 Quasi-periodic motion of the cantilever honeycomb sandwich plate

图7 混沌运动Fig. 7 Chaotic motion of the cantilever honeycomb sandwich plate

4 结论

本文以悬臂边界条件下的矩形蜂窝夹层板作为研究对象,基于Reddy高阶剪切变形理论,运用Hamilton原理和Galerkin方法得到受到面内激励和横向激励联合作用下振动系统的常微分形式的运动方程.通过对悬臂式蜂窝夹层板的非线性振动进行数值模拟,分析在不同激励作用下系统展现出的非线性动力学行为.

在确定悬臂式蜂窝夹层板的材料属性和几何形状等初始参数的情况下,通过数值分析方法得到系统的二维相图、波形图和三维相图.数值模拟表明,随着外激励和面内激励的变化,系统会出现周期运动、多倍周期运动、概周期运动和混沌等多种运动形式.由此可见,激励是影响系统非线性动力学行为的重要因素之一,改变外激励的幅值可以对悬臂式蜂窝夹层板的非线性动力学行为产生较大影响.本文所得结果将对于飞机机翼的减振设计提供一定的指导.

1Allen H G, Neal B G. Analysis and design of structural sandwich panels. Pergamon Press, 1969

2Gibson L J, Ashby M F, et al. The mechanics of two-dimension cellular materials.ProceedingsoftheRoyalSocietyA, 1982,382(1782):25～42

3富明慧,尹久仁. 蜂窝芯层的等效弹性参数. 力学学报, 1999,31(1):113～118 (Fu M H, Yin J R. Equivalent elastic parameters of honeycomb core.ActaMechanicaSinica, 1999,31(1):113～118 (in Chinese))

4Kim H S, Al-Hassani S T S. A morphological elastic model of general hexagonal columnar structures.InternationalJournalofMechanicalSciences, 2001,43(4):1027～1060

5祝涛,王德禹. 蜂窝芯层非线性等效弹性参数. 上海航天, 2008,25(4):15～21 (Zhu T, Wang D Y. Nonlinear equivalent elastic parameters of honeycomb core.AerospaceShanghai, 2008,25(4):15～21 ( in Chinese))

6孙德强,张卫红,孙玉瑾. 蜂窝铝芯的弹性模量和材料效率分析. 力学与实践, 2008,30(1):35～40 (Sun D Q, Zhang W H, Sun Y J. Elastic moduli and material efficiency of aluminum honeycomb cores.MechanicsinEngineering, 2008,30(1):35～40 ( in Chinese))

7陈玳珩,杨璐. 蜂窝板复合材料的等价弹性模量. 力学学报, 2011,43(3):514～521 (Chen D H, Yang L. Analysis of equivalent elastic modulus of a honeycomb sandwich.ActaMechanicaSinica, 2011,43(3):514～521 ( in Chinese))

8陈梦成,平学成,陈玳珩. 正六角形蜂窝夹芯层弯曲刚度理论分析. 固体力学学报, 2012,33(1):26～31 (Chen M C, Ping X C, Chen D H. A theorectical study on the bending rigidity of honeycomb core consisting of right hexagonal cells.ActaMechanicaSolidaSinica, 2012,33(1):26～31 (in Chinese))

9富明慧,徐欧腾,陈誉. 蜂窝芯层等效参数研究综述. 材料导报, 2015,29(3):127～134 (Fu M H, Xu O T, Chen Y. An overview of equivalent parameters of honeycomb cores.MaterialsReview, 2015,29(3):127～134 (in Chinese))

10 Motley M R, Kramer M R, Young Y L. Free surface and solid boundary effects on the free vibration of cantilevered composite plates.CompositeStructures, 2013,96(4):365～375

11 Hao Y X, Zhang W, Yang J. Nonlinear dynamics of cantilever FGM cylindrical shell under 1:2 internal resonance relations.MechanicsofAdvancedMaterialsandStructures, 2013,20(10):819～833

12 杜长城,李映辉. 功能梯度简支矩形板的非线性动力响应. 固体力学学报, 2013,34(4):361～366 (Du C C, Li Y H. Nonlinear dynamic response of simply-supported functionally graded rectangular plates.ActaMechanicaSolidaSinica, 2013,34(4):361～366 (in Chinese))

13 Wang Z X, Shen H S. Nonlinear dynamic response of sandwich plates with FGM face sheets resting on elastic foundations in thermal environments.OceanEngineering, 2013,57(2):99～110

14 Zhang W, Chen J E, Cao D X, et al. Nonlinear dynamic responses of a truss core sandwich plate.CompositeStructures, 2014,108(1):367～386

15 Zhang W, Lu S F, Yang X D. Analysis on nonlinear dynamics of a deploying composite laminated cantilever plate.NonlinearDynamics, 2014,76(1):69～93

16 Ta H D, Noh H C. Analytical solution for the dynamic response of functionally graded rectangular plates resting on elastic foundation using a refined plate theory.AppliedMathematicalModelling, 2015,39(20):6243～6257

17 Azarboni H R, Darvizeh M, Darvizeh A, et al. Effect of forcing frequency on nonlinear dynamic pulse buckling of imperfect rectangular plates with different boundary conditions.Thin-WalledStructures, 2016,107:57～65

18 Parandvar H, Farid M. Nonlinear dynamic response of functionally graded shallow shells under harmonic excitation in thermal environment using finite element method.CompositeStructures, 2016,149:351～361

19 Reddy J N. Mechanics of laminated composite plates and shells: theory and analysis. CRC Press, 2004

Recived 08 October 2016,revised 03 November 2016.

*The project supported by the National Natural Science Foundation of China(11472057)and the Beijing Municipal Education Commission Foundation(KM201711232002).