基于优化设计的印制板组件精细化动力学建模方法

王逸龙 李晶 赵雪梅 曹登庆†

(1.哈尔滨工业大学航天学院, 哈尔滨 150001) (2.中国运载火箭技术研究院, 北京 100076)

引言

随着我国航空航天事业的快速发展,飞行器上电子设备越来越多,电子设备在试验、装配与工作中经常会受到各种随机载荷的影响,从而引发各种各样的故障.为了保证电子设备的可靠性,建立足够精确的动力学模型并对其进行动力学分析是非常必要的.然而,由于电子设备逐渐趋于小型化、模块化和复杂化[1],有限元建模中不可避免的不确定因素,使得建模精度无法满足工程要求.因此对有限元模型进行参数修正并利用其分析电子设备的固有特性,对航天器上电子设备的结构优化与振动控制具有重要意义.

对于电子设备的有限元建模问题,已有大量的研究与报导[2],无论是模态分析[3]还是随机响应分析[4,5]都达到了满意效果.其中,Burmitskih[6]忽略印制板上小元件和焊点的影响,建立简化的有限元模型,并与完整模型的计算结果进行对比,然后对其进行随机振动分析,说明简化模型能够有效模拟印制电路板在随机激励下的响应特性.但是这些研究仅停留在对单块简单印制板的建模与动力学分析上,对螺栓连接型印制板组件的研究较少.Xie[7]使用ANSYS软件对带框架的印制板模型进行了模态分析和随机振动分析,与实验值对比的误差在合理范围内.常涛[8]将弹簧单元应用于螺栓连

接印制板的螺钉连接、接触连接、接头连接有限元建模中,实现了对螺栓连接型印制板的精确建模.李思阳[9]采用接触面绑定的方法,简化处理了螺栓接触中的复杂非线性行为.

随着结构的复杂化,使用这些简化方法已经无法达到工程要求,因此我们有必要借助模型修正的方法提高模型精度.常涛[10]以航天器中使用的某种印制电路板为例,使用N-Updating模型修正软件对印制电路板的物理参数进行识别,验证了这种方法的有效性.郭建英[11]针对螺栓连接板模型,将连接部位直接粘连,并给连接部位的单元定义独立的材料类型,最后通过修正各部位的材料参数值提高了螺栓连接模型的精度.此外,使用ANSYS以及其他商业有限元软件对结构进行模型修正的方法也得到了一定的发展,并成功应用于井架结构[12]、桥梁结构[13]、航天器舱段模型[14]等.

1 基本理论

1.1 螺栓连接型印制板建模方法

20世纪90年代,Pitarresi[2]总结了印制板的有限元建模方法,提出了五种简化方案,之后的研究都是在这五种方法的基础上发展起来的.现在最常用到的方法是将简单成型法与局部等效法相结合,即忽略焊点、小元件和导线的影响,对大元器件采用局部等效法,建立完整模型并按照元件分布、材料和质

量定义不同的材料参数值;元器件与基板、连接板与基板之间的连接采用直接粘连的方式,最后通过修正连接板材料参数值来实现对连接刚度的修正,使得在减少计算量的同时又能够保证建模精度.

1.2 基于ANSYS的灵敏度分析

ANSYS中概率设计模块(PDS)提供了一种将有限元方法与概率统计方法相结合的灵敏度分析方法,用于评估不确定性输入参数对输出参数的影响.其中概率设计方法有蒙特卡罗法和响应面法,最常用到的是蒙特卡罗法,即假设输入参数服从一定概率分布,此后按其分布随机抽取每一个参数值进行一次模拟计算,通过大量重复的随机抽样来模拟真实实验数据.

ANSYS概率设计模块是根据斯皮尔曼(Spearman)等级相关系数[14]来表示输出参数对输入参数的灵敏度.假设有m个输入参数服从概率分布函数X1,X2,…,Xm, 此后按其分布随机抽取每一个参数值进行n次重复模拟计算,相应得到输出参数的序列值y={y1,y2,…,yn},其中第i个输入参数的第j次重复模拟计算所取得的样本值为xij(i=1,2,…,m,j=1,2,…,n).

由第i(i=1,2,…,m) 个输入参数xi的第n次重复模拟计算所取得的样本值xi1,xi2,…,xin和n个输出参数值y1,y2,…,yn构成数据对:

(1)

样本值xi1,xi2,…,xin和输出参数值y1,y2,…,yn在各自整体样本序列中按从小到大顺序排列的位次号分别为Ri1,Ri2,…,Rin,和Si1,Si2,…,Sin,则输出参数和第i个输入参数的Spearman等级相关系数为:

-1≤rsi≤1

(2)

rsi反应了输出参数y和第i个输入参数xi之间的相关性,取值范围为[-1,1].rsi为正表明输出参数y随输入参数xi的增大而增大.而|rsi|反应了输出参数y和第i个输入参数xi之间的相关程度,|rsi|越大,说明输出参数y对输入参数xi越敏感.当两变量之间没有关系时,相关系数为0.

1.3 基于ANSYS优化设计的模型修正

参数修正的目的是通过修正模型参数提高建模精度,而优化设计可以确定模型最优设计方案,从而可以使用优化的方法将模型参数进行优化使得模态特征值能够达到精度要求.

ANSYS程序提供了六种优化设计方法,其中最常用的是一阶优化方法,一阶优化是通过求解设计变量的偏导数来进行的优化.在每次迭代的过程中,用梯度法确定搜索方向,并用线搜索法对目标函数进行最小化,因此每次迭代都分为一系列的子迭代,这就使得每次迭代有多次分析循环,计算量大但是结果精确.这里使用ANSYS优化设计对印制板部件有限元模型进行参数模型修正,模型修正程序流程图见图1.

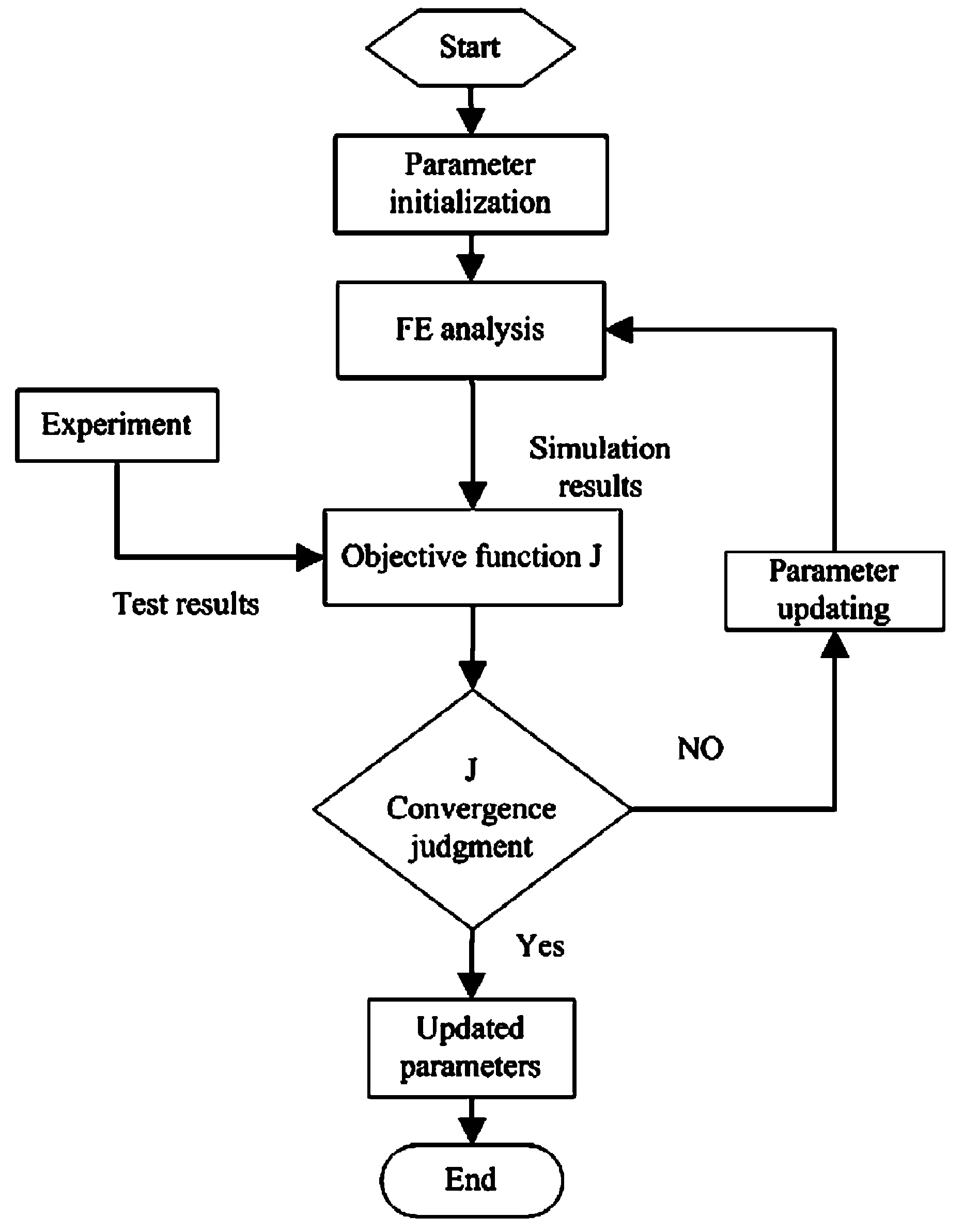
图1 模型修正流程Fig. 1 Flow chart of model updating process

为了对印制板组件进行动力学修正,选择结构前4阶模态频率的相对误差和MAC对角线值共8个特征量组成目标函数如下：

(9)

2 印制板组件参数修正

以航天器上某种螺栓连接型印制板组件为研究对象.采用CAD绘制实体图,然后导入到ANSYS中进行有限元建模,单元选取的是Solid92,建立有限元模型如图2所示.按照元件分布和质量的不同,划分两个区域,分别定义为元件A和元件B.

图2 印制板组件有限元模型Fig. 2 FE model of a PCB

2.1 模态试验

为获得精确的实验数据,利用LMS噪声与振动测试与分析系统(如图3所示)对印制板样本模型(如图4所示)进行了模态实验.使用数据采集器采集印制板部件的振动信号,然后使用LMS数据分析软件对信号进行处理与分析,得到印制板部件的模态频率与模态振型.实验分为自由悬挂和四角支撑两种工况,其中自由悬挂模态实验结果用于模型修正,四角支撑模态实验结果用参数验证.实验装置如图4.

图3 LMS噪声/振动测试与分析系统Fig. 3 LMS noise/vibration test and analysis system

图4 实验装置Fig. 4 Experiment equipments

2.2 灵敏度分析

由于印制板基频较高,实验中采用自由悬挂的方式.由于传感器的相对质量较大,在有限元计算时将传感器的有效质量简化为一个质点加入模型中进行计算.实际计算中,将印制板组件各部件结构参数作为ANSYS灵敏度分析的输入参数.此外,虽然单个传感器质量大约为4.5g,但是传感器上连接头和导线对结果也有一定的影响,而且这些质量影响是不确定的,因此将传感器质量也作为输入参数,然后假设输入的材料参数在物理范围内服从一定的概率分布,详细参数设置如表1,最后按其分布随机抽取每一个参数值进行300次重复模拟计算.

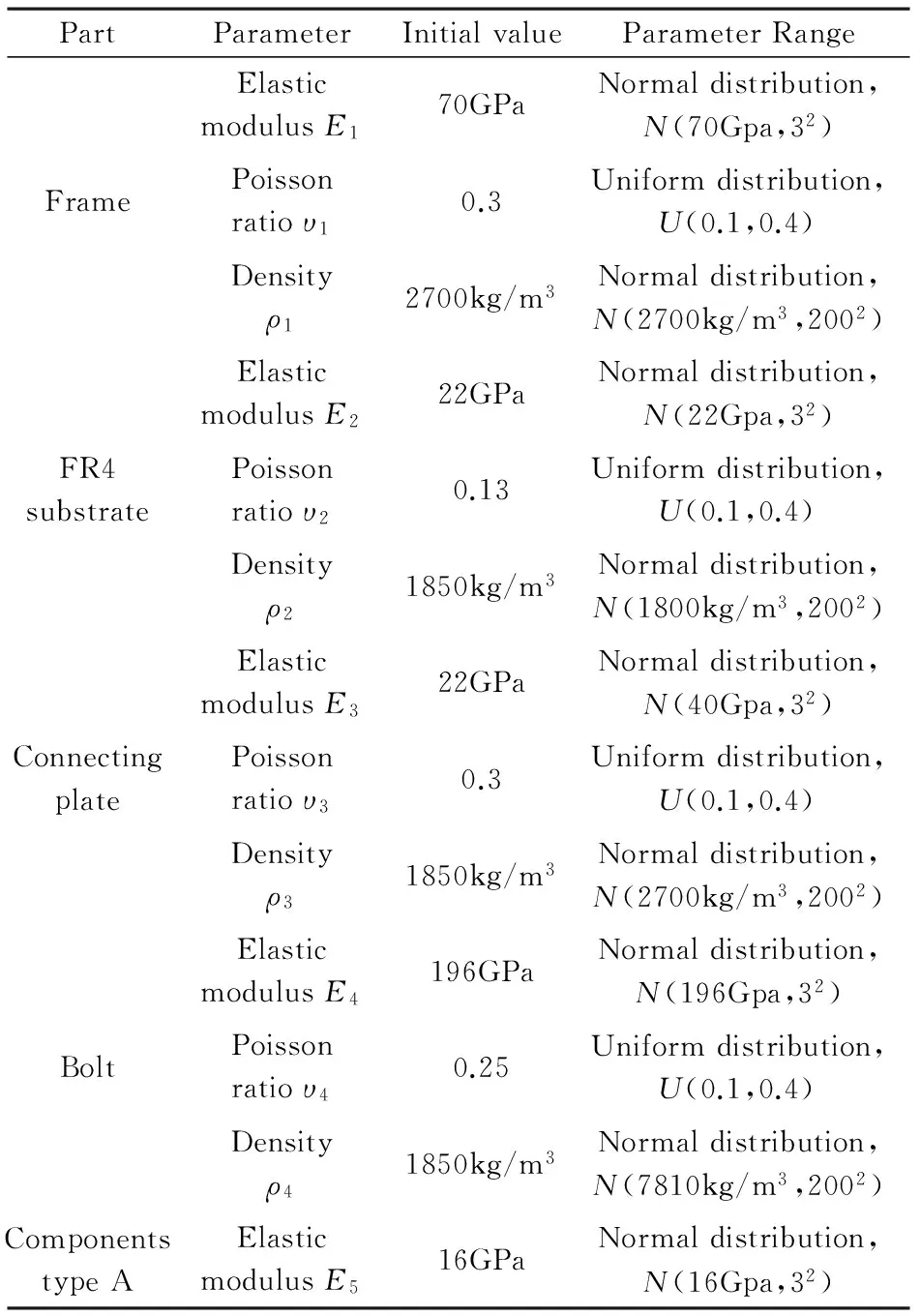
表1 印制板组件输入参数概率分布Table 1 Probability distribution of the PCB parameters

表1 印制板组件输入参数概率分布(续表)Table 1 Probability distribution of the PCB parameters (continued)

选取Spearman等级相关系数来表示输出参数对输入参数的灵敏度,分析印制板组件前4阶模态频率和MAC值对输入参数的随机灵敏度.计算发现:模态频率与MAC对角线值对材料参数值都比较敏感,但是MAC非对角线值的灵敏度较小,因此不再分析MAC非对角线值的灵敏度,计算结果如图5所示.

图5 印制板组件特征值对材料参数灵敏度直方图Fig. 5 Three dimensional histogram of the relationships among sensitivity factor, eigenvalues and material parameters for the PCB

从图5可知,印制板组件的特征值对框架、基板、元件A、元件B的参数和传感器质量都较为敏感,其中对框架、基板的材料参数和传感器质量最为敏感,对连接板和螺钉的材料参数值最不敏感.因此在模型修正中,将以这些敏感参数作为优化设计变量进行参数修正.此外,在对印制板部件简化建模的时候,我们将印制板基板和连接板部分采用直接粘连的方式连接,而实际上螺栓连接并不是完全面面接触的,本文的建模相当于忽略了螺栓连接部位的建模误差,因此在进行修正参数选择的时候,同样将连接板材料参数值也作为设计变量进行参数修正.

2.3 模型修正

图6 印制板组件目标函数J收敛曲线Fig. 6 Convergence curve of the objective function J for the PCB

PartElasticmodulusE/GPaPoissonratioυDensityρ/(kg/m3)OriginalUpdatedOriginalUpdatedOriginalUpdatedFrame7064.2740.300.31727003520FR4substrate2227.7330.130.10118503390Connectingplate409.0220.300.31327002770ComponentstypeB1610.0510.300.29124201500ComponentstypeA129.0000.250.25020004990

模型修正前后的模态频率计算结果与实验测试结果对比见表3,修正前模态频率的误差平均在20%左右,模型精度较差,而修正后建模精度均在±2%以内,达到有限元的模拟精度.修正后,前4阶振型与实验测试振型对比见图7,实验分析和有限元分析的振型一致,由于是自由悬挂,1阶振型表现为整体的扭转模态,2阶、3阶、4阶模态表现为基板的弯曲模态.

表3 印制板组件模型修正前后模态频率结果对比Table 3 Comparison of natural frequencies for the PCBA before and after model updating

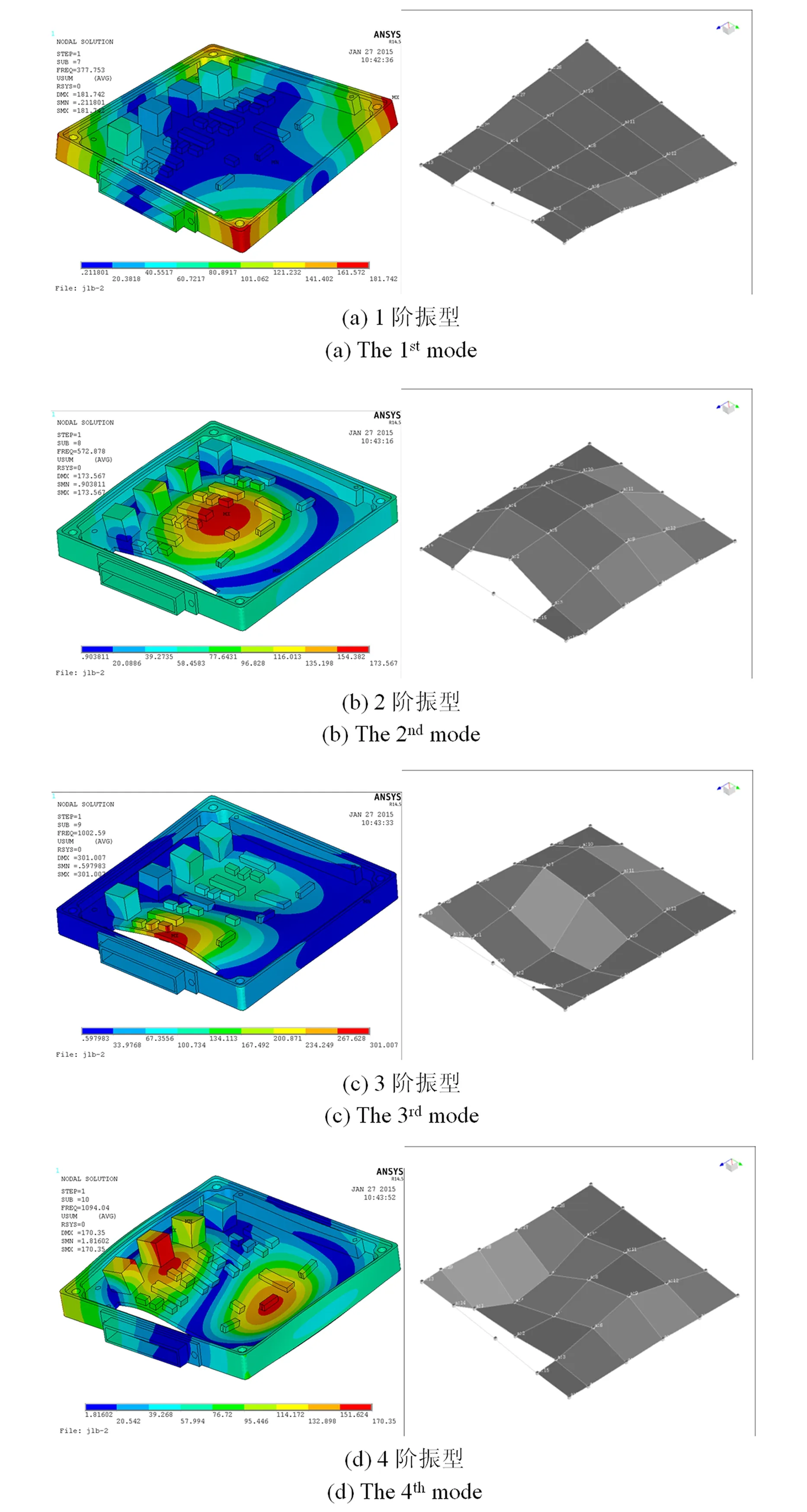
图7 印制板组件修正后模态振型(左)与实验测得模态振型(右)对比Fig. 7 Comparison of updated modes (left) and the modes from test results (right)

模型修正前后MAC值对比见图8,修正前MAC对角线值仅大于70%而非对角线值接近10%,修正后一阶模态MAC对角线值略有降低,但是2、3、4阶模态MAC对角线值均有很大幅度提升,整体对角线值均在80%以上,提高了模态振型的预示精度.

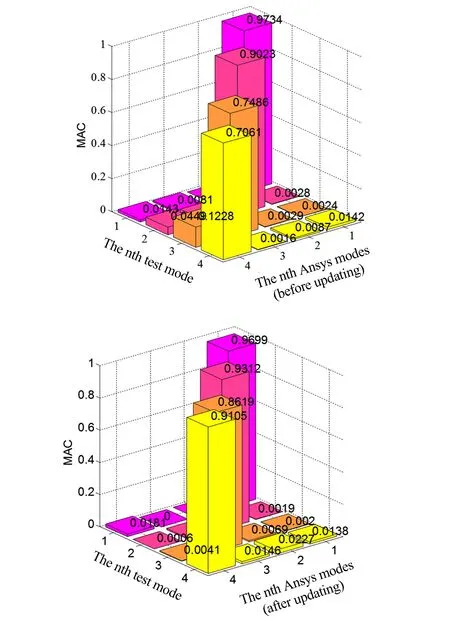
图8 印制板组件修正前后ANSYS结果与实验结果的MAC值柱状图Fig. 8 MAC values based on ANSYS results and experimental results before and after updating

2.4 参数验证

模型修正要求修正后模型不仅能够反映所修正模型的动力学特性,而且更改参数或者更改边界条件后仍然能够达到很好的预示精度.本文通过修改边界条件来验证修正后模型的有效性.采用四角支撑模型,将修正后参数应用到四角支撑模型中,与实验值对比达到精度要求,则说明修正后参数达到修正要求.

将表2中修正参数代入四角支撑的印制板组件有限元模型中,进行有限元模态分析,将修正后印制板组件四角支撑模型计算结果与实验测试结果对比如表4.对比可知,修正后模型前4阶模态频率吻合较好,其中前三阶频率误差均在±3%以内,达到有限元的模拟精度.MAC对角线值都在70%以上,模态相关性较好.说明修正后模型达到工程精度要求,能够有效模拟印制板组件的动力学特性.

表4 修正后印制板组件四角支撑模型分析结果对比Table 4 Comparison of the natural frequencies from the updated ANSYS model and experimental results under four-point constraint for PCBA

3 结论

以航天器上某螺栓连接型印制板组件为研究对象,基于ANSYS优化设计对印制板组件进行模型修正.以模态测试结果作为修正的目标值,首先使用ANSYS灵敏度分析确定了优化设计的设计变量,然后使用ANSYS优化设计模块对印制板组件进行了参数修正,最后通过改变边界条件验证了修正后参数的有效性.得到以下结论:

(1)灵敏度分析结果表明印制板组件的固有频率和MAC值对角线元素对框架、基板、元件的参数和传感器质量的灵敏度较高,根据灵敏度分析结果确定这些敏感参数作为设计变量,减少了优化设计中设计变量的个数,从而提高优化效率;

(2)针对螺栓连接问题,考虑螺栓连接建模误差,将连接板材料参数值也作为设计变量,经过模型修正实现了对螺栓连接印制板组件的精确建模,说明通过修正连接处材料参数值可以提高模型精度;

(3)基于优化设计的模型修正方法运算简单、目标明确,修正后模型达到了工程建模精度要求,改变边界条件后,修正后参数仍然适用,说明综合考虑灵敏度分析结果和建模误差的优化设计方法可以满足实际应用的要求.

1霍曼,邓中卫. 国外军用飞机航空电子系统发展趋势. 航空电子技术, 2005,35(4):5～10 (Huo M, Deng Z W. Development trend of foreign military avionics.AvionicsTechnology, 2005,35(4):5～10 (in Chinese))

2Pitarresi J, Primavera A. Comparison of modeling techniques for the vibration analysis of printed circuit cards.JournalofElectronicPackaging, 1992,114(4):378～383

3Pitarresi J, Geng P, Beltman W, et al. Dynamic modeling and measurement of personal computer motherboards. In:Proceedings of the Electronic Components and Technology Conference, 2002 Proceedings 52nd, IEEE, 2002: 97～603

4李春洋. 印制电路板有限元分析及其优化设计[硕士学位论文]. 长沙:国防科学技术大学, 2005 (Li C Y. Finite element analysis and optimization design of the printed circuit board[Master Thesis]. Changsha: National University of Defense Technology, 2005 (in Chinese))

5罗圣和. 印制电路板组件的振动分析与控制[硕士学位论文]. 西安:西安电子科技大学, 2012 (Luo S H. Analysis and control for vibration of the printed circuit board assembly[Master Thesis]. Xi′an: Xidian University, 2012 (in Chinese))

6Burmitskih A V, Lebedev A P, Levitskiy A A, et al. Printed Circuit Board vibration analysis using simplified finite element models. Proceedings of International Siberian Conference on Control and Communications (SIBCON 2013), IEEE, 2013:1～4

7Xie M, Huang D, Zhang T, et al. Dynamic analysis of circuit boards in ANSYS. Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation IEEE, 2006: 1403～1407

8常涛. 电子设备结构有限元精确建模方法研究[硕士学位论文]. 南京:南京航空航天大学, 2012 (Chang T. Research on precise finite element modeling method of electronic equipment structure[Master Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese))

9李思阳,陈丽丽. 螺栓紧固型印制板组件简化建模研究. 现代电子技术, 2013,36(2):68～70 (Li S Y, Chen L L. Research on simplified modeling of bolted fastening printed circuit board assembly.ModernElectronicsTechnique, 2013,36(2):68～70 (in Chinese))

10 常涛,郭勤涛,张保强. 应用模型修正方法的印制电路板参数识别. 振动、测试与诊断, 2013,33(3):509～513 (Chang T, Guo Q T, Zhang B Q. Parameter identification of the printed circuited board using model updating method.JournalofVibration,Measurement&Diagnosis, 2013,33(3):509～513 (in Chinese))

11 郭建英. 螺栓连接板结构的动力模型修正. 南京:南京航空航天大学, 2012 (Guo J Y. Structural dynamic model updating of a bolted plate. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese))

12 刘金梅,韩国有,周国强. 基于灵敏度分析的井架结构模型修正方法研究. 科学技术与工程, 2009,9(9):2366～2370 (Liu J M, Han G Y, Zhou G Q. Research on model updating method of derrick structures based on sensitivity analysis.ScienceTechnologyandEngineering, 2009,9(9):2366～2370 (in Chinese))

13 陈彦江,程永欢,李勇等. 基于参数灵敏度分析的连续刚构桥有限元模型修正. 公路, 2014,7:144～149 (Chen Y J, Cheng Y H, Li Y, et al. FE model updating for continuous rigid frame bridge based on parameter sensibility analysis.Highway, 2014,7:144～149 (in Chinese))

14 郭其威,吴松,刘芳等. 航天器模态分析—试验体系工程实践研究. 动力学与控制学报, 2014(3):274～278 (Guo Q W, Wu S, Liu F, et al. Research on engineering practice of modal analysis—test of spacecraft.JournalofDynamics&Control, 2014(3):274～278 (in Chinese))

15 王静龙,梁小筠. 非参数统计分析. 北京:高等教育出版社, 2006. (Wang J L, Liang X Y. Nonparametric statistics analysis. Beijing: Higher Education Press, 2006 (in Chinese))