转子-滑动轴承系统支承松动-碰摩故障动力学行为及评估方法*
蒋勉 伍济钢 彭鑫胜 宾光富
(湖南科技大学 机械设备健康维护湖南省重点实验室,湘潭 411201)
引言
转子-滑动轴承系统是旋转机械的重要组成部分.支承松动是其常见的故障,安装质量不高及长期振动都会引起机械部件之间的松动.松动通常可分为旋转部件松动和支承松动两种形式,在发生支承松动的转子系统中,支承松动程度会随着系统的运转不断地发展.当系统运转所产生的不平衡力大于支座所受重力时,支座就会跳动,从而会发生一定程度的碰摩现象.伴随碰摩故障的产生,使得整个系统的运动变得更加复杂,对系统的影响程度也会随着松动间隙的变化而变化.近年来国内外许多学者针对松动-碰摩故障转子系统动力学问题从不同角度进行了研究[1-6].褚福磊等[7]讨论了转速变化时支承松动转子-轴承系统的多种形式周期、拟周期和混沌运动,指出这类系统某些周期运动的映射点结构具有慢变的特性.周鹏等[8]研究了转子松动由小变大引起的慢变过程,得出一系列动力学行为特点与规律;马辉等[9]将单一支承松动故障与松动-碰摩故障的转子进行比较,得出碰摩能够减小松动引起的低频振动等.但目前很少有文章涉及到对转子-滑动轴承系统支承松动状态评估方法的研究.
本文建立了带有支承松动-碰摩故障的转子系统非线性动力学模型,采用数值模拟的方法计算分析了其动力学行为规律和特征,得到松动间隙变化对系统动力学行为的影响程度.根据动力学分析结果,提出基于动力学行为非线性度量的方法建立松动间隙大小与非线性度之间的对应关系,为转子-滑动轴承系统支承松动评估提供新方法.
1 松动-碰摩转子系统动力学模型
图1为带有支承松动-碰摩的转子-滑动轴承系统,两端有2个相同的滑动轴承支承,假设右端轴承支座与基础之间发生松动.o1为轴瓦几何中心,o2为转子几何中心,o3为转子的质心.在两端轴承处的转子等效集中质量为m1,转子在圆盘处等效集中质量为m2,m3为轴承支承座的等效集中质量.k为弹性轴线性刚度,c1为两端轴承处的等效阻尼,c2为转子在圆盘处的阻尼,kb,cb分别为支承松动处的刚度和阻尼系数.忽略圆盘与轴承之间弹性轴的质量,设松动间隙为δ.

图1 支承松动-碰摩故障转子系统Fig.1 Rotor system with supporting loosening-rubbing fault
假设滑动轴承-转子系统右端轴承轴心在水平和垂直方向相对于平衡位置的振动位移分别为x1,y1,圆盘中心在水平和垂直方向相对于平衡位置的振动位移分别为x2,y2,松动故障的左端轴承轴心在水平和垂直方向相对于平衡位置的振动位移分别为x3,y3.由于松动端支承座水平方向的松动间隙非常小,所以仅考虑支承座垂直方向的振动位移y4.
支承松动是导致转子系统非线性动力学行为变化最常见的非线性因素之一,在转子系统老化松动等情况下表现尤为突出.对于图1中转子-轴承系统支承松动间隙产生的垂直方向弹性力采用如下的定义[10]:
F弹=ky4+kby43
(1)

1.1 碰摩力
当转子系统的支承出现松动故障时,某些情形下会在转子与定子之间伴随着发生碰摩故障,其对转子系统动力学行为的影响不可忽略.为研究方便,对碰摩转子系统进行了简化.不考虑摩擦的热效应,并假定转子与定子部件的碰撞为弹性碰撞,变形为弹性变形,碰摩为局部碰摩.设转子与定子间的初始间隙为δ1,与运动周期相比碰摩的时间非常短,此时可用弹性碰撞模型,再假设接触面间的摩擦为库伦摩擦.如图2为转子碰摩故障局部示意图,xoy为固定坐标系,o表示转子的中心位置,(x,y)表示转子中心坐标,φ为碰摩时的涡动角位移,ω为转子的角速度.另外,径向力Fn和切向力Fr可表示为:
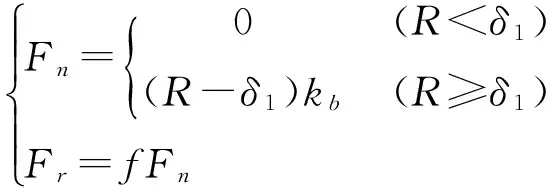
(2)
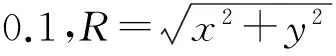

(3)

图2 转子碰摩局部示意图Fig.2 Local schematic diagram of rotor rub
1.2 转子系统动力学模型
基于上述理论分析,结合转子动力学方程分别得到支承松动-碰摩故障的滑动轴承-转子系统动力学方程如下:

(4)
Fx=sfx,Fy=sfy
(5)
当转子系统支承发生松动时,cb、kb可表示为:
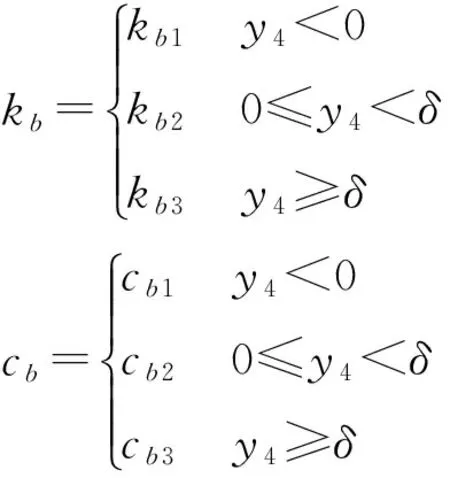
(6)
这是一个带有分段线性刚度和阻尼的非线性振动系统.当振动位移y4∈[0,δ]时,可使用等效的二阶方程对等效刚度进行求解[12].
2 支承松动-碰摩故障动力学行为分析
由于非线性动力系统难以求出其解析解,本文采用4-5阶变步长Runge- Kutta法,对动力学模型(4)进行数值仿真研究.计算中积分步长为1/512.其中数值计算时动力学方程(4)中所采用的参数值根据参考文献如表1所示.
需要说明的是,本文共选取了左端轴承轴心、右端轴承轴心、圆盘形心,松动端支承座五个点进行数值仿真分析.由于系统中松动端支承座、松动端轴承轴心与圆盘竖直方向振动幅值较大,支承松动处的非线性因素对于动力学行为影响明显,所以本文选用此处来分析系统的动力学行为特性.

表1 仿真选取参数值Table 1 Simulation parameters
当转子-滑动轴承系统正常运行时,由于油膜力的影响,转子各点在平衡位置附近微幅振动,且按一定的规律严格的周期性运动,系统平稳运行.如图3(a)、(b)所示,系统呈现周期运动,且正负半轴对称,轴心轨迹为椭圆状.

图3 松动间隙δ=0转子-滑动轴承系统的响应Fig.3 Responds of the rotor-slide bearing system when the looseness gap δ=0
当支承出现较小松动间隙时,系统表现出的非线性程度较弱.图4为松动间隙δ=0.00002时圆盘竖直方向时域图、松动端支承竖直方向时域图、轴心轨迹、轴心幅频特性.从图4(a)(b)(c)(d)可见,系统由于松动间隙较小,并未产生碰摩现象,其振动幅值变化较小,圆盘振动特性成周期运动;弹性力与油膜力的影响,使得松动端支承座上出现了微弱的冲击,轴心轨迹与图4(b)基本一致,转子周期运动,对系统影响非常小.

图4 松动间隙δ=0.00002时转子-滑动轴承系统的响应Fig.4 Responds of the rotor-slide bearing system when the looseness gap δ=0.00002
随着支承松动间隙的增大,除周期运动外,开始呈现拟周期运动.定子与转子发生局部碰摩,其动态响应特性与转子碰摩过程的幅值程度有关.当转子发生碰摩时,其碰摩点并非始终处于接触状态,而是碰摩与弹开不断交替变化,松动与碰摩的耦合故障转子-轴承系统响应处于同步拟周期状态.如图5(a)(b)可见,系统由于受到非线性弹性力与碰摩力的影响,受到的冲击增大,系统开始呈现规律性的拟周期运动.同时转子轴心轨迹明显增大,其轨迹不再是规则椭圆状,幅频特性图中也存在了较小的连续谱峰.说明系统在松动间隙增大的条件下,每个周期都出现了冲击,系统动力学行为的非线性程度增强,对系统的运行影响程度逐渐增大.
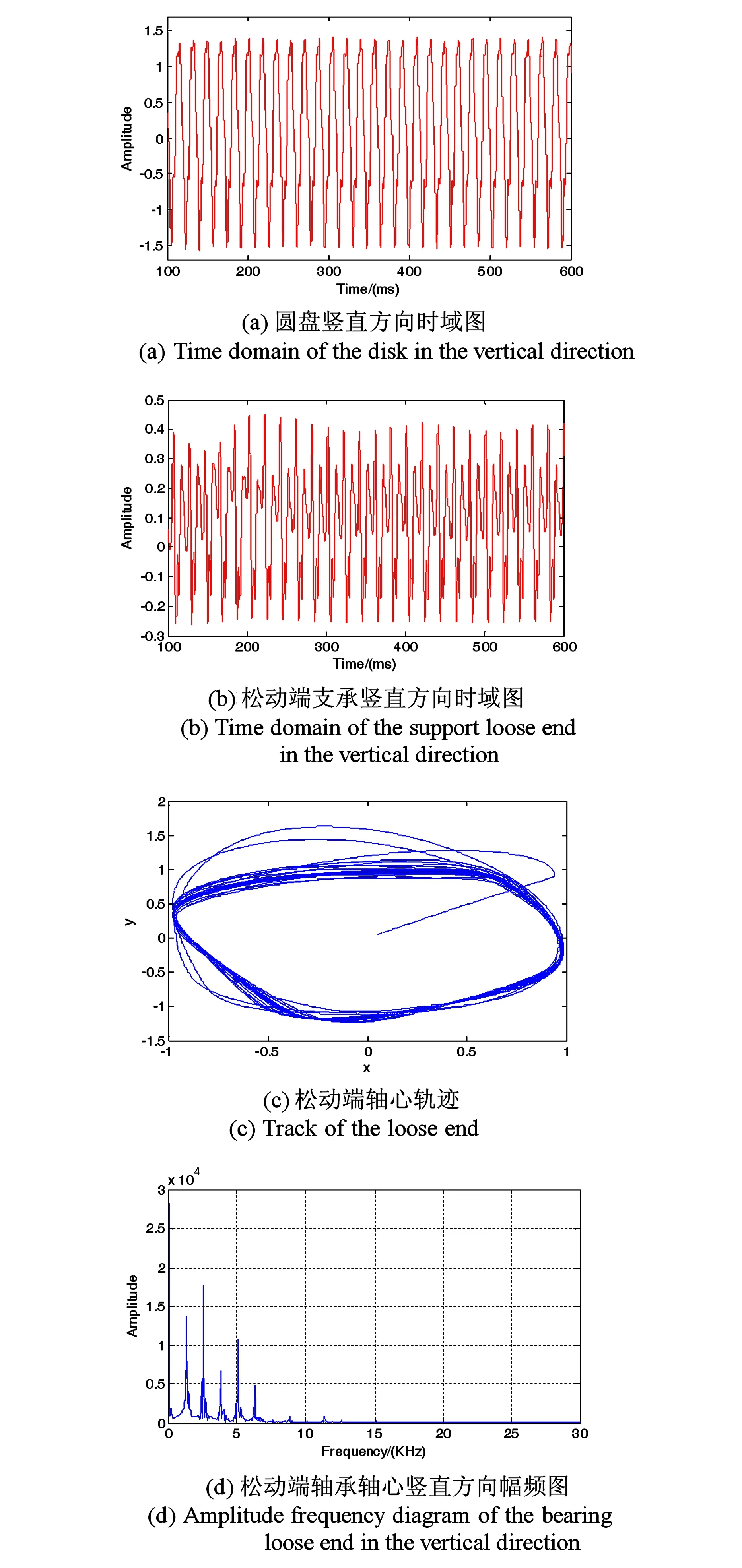
图5 松动间隙δ=0.0002时转子-滑动轴承系统的响应Fig.5 Responds of the rotor-slide bearing system when the looseness gap δ=0.0002
当松动间隙继续增大,图6为松动间隙为δ=0.002时转子系统特性图,从图上可知,松动间隙增大时非线性弹性力与碰摩力对系统的影响增大,转子系统的运动形式越来越复杂,不再是周期运动或拟周期运动,而是进入混沌运动.从图6的轴心轨迹图上可见,随着松动间隙的增大,转子与定子之间碰摩的面积增大,逐渐从局部向整圈碰摩转化.从图6的幅频图上可见,在连续谱峰上发现,除高频分量外,在低频处有很高的幅值峰值.

图6 松动间隙δ=0.002时转子-滑动轴承系统的响应Fig.6 Responds of the rotor-slide bearing system when the looseness gap δ=0.002
根据以上分析,在考虑碰摩故障的情况下,系统运动特性越来越复杂,出现周期运动-拟周期运动-混沌运动变化,动力学行为的非线性特性也越来越明显.
3 基于动力学行为非线性度量的转子系统松动状态评估
转子-滑动轴承系统动力学行为属于非线性动力学行为.当支承松动出现时,由于非线性弹性力与碰摩力的产生将导致整个转子系统动力学行为发生相应变化,非线性效应更加明显,其动力学行为变得更加复杂.松动间隙越大,系统动力学行为的非线性程度越明显,使得滑动轴承-转子系统具有更加复杂的非线性动力学行为.为了描述支承松动间隙的大小对转子-轴承系统动力学行为的影响程度,引入动态系统动力学行为系统非线性度量定义[12,13]如下:

图7 非线性度量Fig.7 Nonlinearity measure
如图7所示,在相同的输入条件u下比较通过所研究的非线性系统N的动力学方程N(u)与相应线性近似系统G的线性动力学行为G(u)的差异,两者动力学行为差异大即系统动力学行为的非线性程度更高.
系统非线性度量的定义可知,对转子-轴承系统非线性度量需要建立一个线性近似系统模型G作为其比较标准和量化计算的基础.本文采用对于原非线性模型(4)中的非线性项进行泰勒展开的办法得到线性近似模型G.将油膜力Fx、Fy对变化位移Δx、Δy进行泰勒展开,并去掉高阶项[15],可得到转子-轴承系统动力学行为在某一时间点的动态线性近似油膜力为式(6).其中hxx,hxy,hyx,hyy为单位位移所引起的油膜力增量,即油膜力刚度系数;dxx,dxy,dyx,dyy为单位速度所引起的油膜力增量,即油膜力阻尼系数.
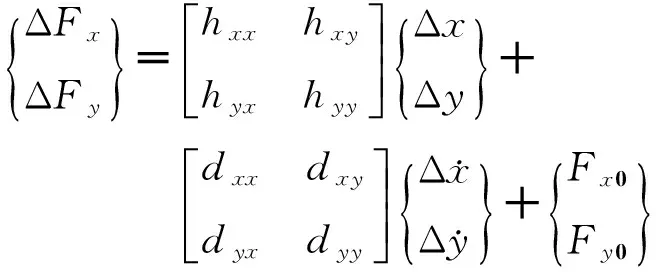
(6)
同样,对转子-轴承系统松动端支承座弹性力F弹=ky4+kby43在平衡点进行泰勒展开,去掉两阶以上函数项可得到其线性近似如下:
F弹s=ky4
(7)
基于油膜力和松动端弹性力的线性近似化处理,可得到转子-轴承系统线性近似模型G:

(8)
由于振动响应代表了转子-轴承系统的动力学行为特征,基于机械振动信号对支承松动-碰摩故障转子-轴承系统动力学行为进行量化,引入L2范数如下:
(9)
采用L2范数可以量化转子-轴承系统动力学行为相对于某个线性近似系统动力学行为的差异程度,同时描述非线性程度的强弱.当转子-轴承系统的松动间隙大小发生变化时,其非线性系统动力学行为也发生相应的变化,则非线性程度也发生变化[13-15].为了方便对于非线性度进行具体量化比较,定义振动响应非线性度计算公式[13]为:
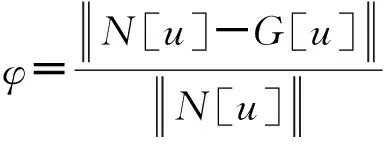
(10)
当转子-轴承系统不存在耦合故障时,其系统动力学行为是非线性的.当转子-轴承系统存在耦合故障时,其系统的非线性动力学行为更加复杂,即动力学行为非线性程度更高.同时,当系统存在不同松动间隙大小时,其动力学行为非线性度将是不同的.在考虑碰摩力的情况下,通过改变支承松动间隙,分析松动间隙对转子-滑动轴承系统动力学行为的影响,运用振动响应非线性度评估方法,并对影响程度进行量化计算.
本文共对等间隙的81个采样点进行数值仿真,并计算对应情况下的振动响应非线性度量值.如图8表示转子-滑动轴承系统振动信号非线性度量估计值与松动间隙大小的关系.图中离散点表示各松动间隙点所对应的系统非线性度量估计值,曲线为基于非线性度量估计值的非线性拟合曲线,用于说明振动响应非线性度变化趋势.
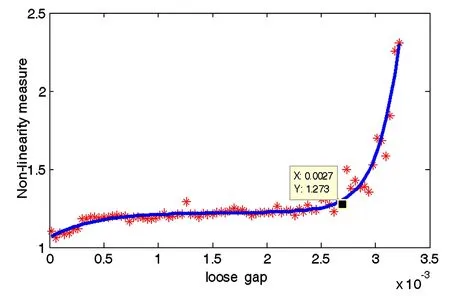
图8 振幅信号非线性量估计值与松动间隙对应关系Fig.8 Relationship between nonlinearity estimation and loosen gap of the amplitude signal
如图8所示,当松动间隙0<σ<0.0027时,其非线性度随着松动间隙的增大,整体有小幅度的上升趋势,说明在松动间隙较小时的非线性弹性力与碰摩力影响较小,所以对系统的影响不明显但呈缓慢的增长趋势.当σ>0.0027时,系统进入混沌运动,系统的非线性度急剧上升,说明松动间隙超过该点,松动对系统动力学行为的影响变得严重,急需对松动故障进行处理.从拟合曲线趋势可知,考虑碰摩故障情况下,松动对转子-滑动轴承系统的影响成特定指数增长,从而能够直观地看出松动间隙与影响程度(非线性度)的对应关系.从曲线的指数型增长特性可知,与松动间隙的发展过程是相符合的.
4 结论
本文针对转子-滑动轴承系统发生支承松动-碰摩故障动力学行为进行了分析,并提出基于动力学行为非线性度量的转子-轴承系统支承松动状态评估方法.通过建立带有支承松动故障的转子-滑动轴承系统局部碰摩力的动力学方程.应用数值仿真分析方法对松动-碰摩故障转子系统动力学行为进行分析发现:发现随着松动间隙的增大,其动力学行为发生周期运动-拟周期运动-混沌运动的形式转变.
进一步,本文提出了基于动力学行为非线性度量的转子-滑动轴承系统支承松动状态评估方法,建立了松动间隙与动力学行为非线性度的关系.结果表明:随着松动间隙的增大,影响程度呈指数增长,通过非线性度的拟合趋势实现对转子-滑动轴承支承松动状态的评估.本文的研究可为转子-滑动轴承系统支承松动状态评估提供理论基础和支撑.
1Qin Z, Han Q, Chu F L. Bolt loosening at rotating joint interface and its influence on rotor dynamics.EngineeringFailureAnalysis,2016,59:456-466
2刘杨,李炎臻,太兴宇等. 转子-滑动轴承系统松动-碰摩耦合故障分析. 振动工程学报,2016,29(3):549~554(Liu Y,Li Y Z,Tai X Y,et al. Characteristic analysis of looseness-rubbing coupling fault in rotor-sliding-bearing system.JournalofVibrationEngineering,2016,29(3):549~554(in Chinese))
3罗跃纲,李振平,刘长利等. 转子系统松动与碰摩耦合故障非线性特性研究. 中国机械工程,2003,16(2):1224~1227. (Luo Y G, Li Z P, Liu C L, et al. Study on Nonlinear behavior of rotor system with pedestal looseness and rubbing faults.ChineseJournalofMechanicalEngineering,2003,16(2):1224~1227(in Chinese))
4Lu K, Jin Y, Chen Y, et al. Stability analysis of reduced rotor pedestal looseness fault model.NonlinearDynamics,2015,82(4):1611~1622
5陈果.含不平衡-碰摩-基础松动耦合故障的转子-滚动轴承系统非线性动力响应分析. 振动与冲击,2008,27(9):100~104(Chen G. Non-linear dynamic response analysis of rotor ball bearing system including unbalance-rubbing-looseness coupling faults.JournalofVibrationandShock,2008,27(9):100~104(in Chinese))
6罗忠. 转子-轴承系统中滚动球轴承的非线性动力学相似特性研究. 动力学与控制学报,2016,14(3):223~228(Luo Z. Similarity research on the nonlinear dynamic characteristics of rolling bearing in rotor-bearing system.JournalofDynamicsandControl,2016,14(3):223~228(in Chinese))
7Chu F L, Tang Y. Stability and non-linear responses of a rotor-bearing system with pedestal looseness.JournalofSoundandVibration,2001,241(5):879~893
8周鹏,刘挺,冯霏等. 松动-碰摩发展过程中的非线性慢变问题. 振动、测试与诊断,2012,32(1):123~126. (Zhou P, Liu T, Feng F, et al. Nonlinear slowly varying problems in development process of loose-rubbing.JournalofVibration,Measurement&Diagnosis,2012,32(1):123~126.(in Chinese))
9马辉,太兴宇,汪博等. 松动-碰摩耦合故障转子系统动力学特性分析. 机械工程学报,2012,48(19):80~86(Ma H, Tai X Y, Wang B, et al. Dynamic characteristic analysis of a rotor system with pedestal looseness coupled rub-impact fault.ChineseJournalofMechanicalEngineering,2012,48(19):80~86(in Chinese))
10Chen C, Yau H T. Chaos in the imbalance response of a flexible rotor supported by oil film bearings with nonlinear suspension.NonlinearDynamics,1998,16:71~98
11刘占生,崔亚辉,叶建槐. 非线性油膜力和啮合作用下齿轮系统的振动特性研究. 中国电机工程学报,2009,29(23):84~91(Liu Z S, Cui Y H, Ye J H. Research on vibration characteristics of gear system with nonlinear oil film force and mesh force.ProceedingsoftheCSEE,2009,29(23):84~91(in Chinese))
12Desor C A, Wang Y T. Foundations of feedback theory for nonlinear dynamical systems.IEEETransonCircuits&Systems,1980,CAS-27(2):104~105
13Helbig A, Marquardt W, Allgower F. Nonlinearity measures: definition, computation and applications.J.ProcessControl.2000,10:113~123
14刘忠伟. 惯性往复振动机械非线性支承刚度研究及应用. 河南:河南工业大学,2012(Liu Z W. Research and application on nonlinear supporting stiffness for inertial reciprocating machines. Henan: Henan University of Industrial,2012(in Chinese))
15傅彩芬. 非线性系统的非线性度分析及增益调度控制. 北京:华北电力大学,2004(Fu C F. Nonlinearity measure analysis and gain-scheduling control for nonlinear systems. Beijing: North China University of Electricity,2004(in Chinese))
16李明,李自刚. 完整约束下转子-轴承系统非线性振动. 北京:科学出版社,2014(Li M, Li Z G. Nonlinear vibration of rotor-bearing system under holonmic constraints. Beijing: Science Press,2014(in Chinese))
17Yang Y, Cao D Q, Yu T H. Prediction of dynamic charateristics of a dual-rotor system and experimental study.InternationalJournalofMechanicalSciences,2016,115-116:253~261
18曹青松,向琴,熊国良. 机械松动现象与故障特征性研究综述. 噪声与振动控制,2015,35(2):1~6(Cao Q S, Xiang Q, Xiong G L. Review of mechanical looseness phenomena and failure characteristics study.NoiseandVibrationControl,2015,35(2):1~6(in Chinese))

