改进单纯形最优搜索的可视化仿真与训练
魏晓玲(广州工商学院 计算机科学与工程系,广东 广州 510850)
遗传、模拟退火、蚁群、粒子群、神经网络以及单纯形算法成为近期研究的热点,一度成为主流寻优方法,但由于算法自身的缺陷造成其适用范围具有一定的局限性,如遗传算法搜索速度慢,易出现早熟[1];模拟退火算法进入最有希望搜索的区域较慢,运算效率低[2];蚁群算法收敛速度慢、易陷入局部最优[3];粒子群算法处理复杂的多峰搜索问题时容易产生早熟收敛[4];人工神经网络容易出现难以解释的结果[5];单纯形算法易出现最长边较长,但体积已接近零的病态现象[6].单纯形算法最早是由Splendley等[7]于1962年提出,随后为了提高正规单纯形的搜索速度,Neledr和Mead[8]在Splendley的基础上于1965年提出了N-M单纯形算法.单纯形算法被称为序贯性寻优方法,即依据于上次的寻优结果,及时调整寻优方向和步长,其局部寻优速度仍是某些算法所不能替代的,鉴于其优点部分学者将单纯形融入到其它算法中,如遗传算法[9-13]、人工鱼群算法[14-15]、量子粒子群算法[16-17]、自适应步长的花朵授粉算法[18]以及人口迁移算法[19]等,并且取得了较好的效果,有效的弥补了算法的自身不足.也有大量的学者将单纯形寻优算法应用到生产生活中,例如生产工艺试验设计[20-24]、教学方法改进[25]、近邻链查询[26-29]等.近期学者们研究单纯形主要集中在两方面,将单纯形应用在实验设计中,或与其他算法融合寻优.单纯形的可视化仿真的设计研究相对较少,故本研究拟借助于MATLAB软件,实现单纯形的可视化仿真的设计;并进行函数仿真训练,验证效果,使寻优轨迹更直观.
1 单纯形最优搜索数学模型
1.1 单纯形简介
正规单纯形是指在S维空间中,以S+1个顶点构成的最简单的图形,其寻优过程中不是沿着一个方向进行搜索,而是对S维空间的S+1个顶点上的函数进行比较.丢掉最坏的点,代之以新点,从而构成新的单纯形,其寻优过程类似下图1.它是迭代之前,先确定最优的方向,然后逐步向最优逼近的过程.N-M单纯形在正规单纯形的基础上,通过增加扩张和压缩步骤,将正规单纯形扩展至任意单纯形,加速收敛速度,减少迭代次数.
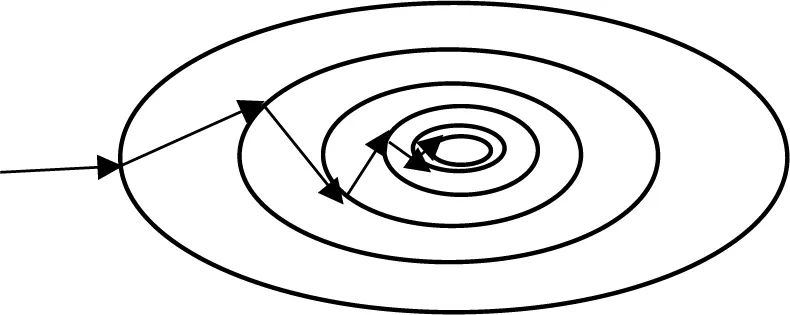
图1 单纯形寻优过程模拟图Fig.1 The simulation diagram of simplex optimization
1.2 初始单纯形的构造
初始单纯形构造过程中,由于最优结果的方向是未知的,因此初始单纯形的构造一般设计为正规单纯形.然而实际应用中,由于各因素的量纲不同,采用统一的搜索步长很难满足各因素快速收敛的需求.Long[30]在1969年提出了一种系数表构成初始单纯形的方法,但其局限性在于只能构造10个因素以内的单纯形.也有部分研究者为了初始布点的均匀性,用均匀设计来构造初始单纯形顶点,取得了较好的应用.而本研究主要针对函数进行测试,不涉及到实际生产应用及各因素对应的量纲问题,故只介绍正规单纯形顶点构造方法,即单纯形RS空间中多面体的每条棱长(步长a)相等,且满足以下定义:
定义1{V1,V2,…,VS,VS+1}为RS空间的某一单纯形S+1顶点的位置矢量,vi表示S个变量的取值.
定义2令S个因素各取一起始水平的点为x0,则有V1=x0.Vi=x0+z(i) (i=2,3,…,S+1),其中z(i)为S维矢量,z(i)=[q,…,q,p,q,…,q]T,上式中:
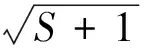
满足以上条件,可证明S+1个顶点的正规单纯形各棱长均相同,若令初始点坐标为V1=[v1,v2,…,vs],则剩余各顶点的坐标为,即初始单纯形顶点:
V2=[v1+p,v2+q,…,vs+q],
V3=[v1+q,v2+p,…,vs+q],
………………
Vs+1=[v1+q,v2+q,…,vs+p].
1.3 单纯形最优搜索设计
Step1给定初始单纯形的一个顶点V(1)及搜索步长a,依据1.2中定义2计算出初始单纯形的其余顶点:V(2),……,V(S),V(S+1),并计算出单纯形顶点的函数值:f(V(1)),f(V(2)),……,f(V(S)),f(V(S+1)).
Step2比较单纯形各顶点的函数值,确定函数最优V(H)点,最差点V(L)点及次差V(C)点,并检验︱(f(V(H))-f(V(L)))︳≤ε(ε为收敛精度),若满足条件,则输出最优点为V(H)点,最优值为f(V(H)),计算结束,若不满足条件转入第Setp3步反射运算.
Step3反射运算
(1)计算剔除最差点V(L)后的重心V(S+1)(H).
i=1,2,……,S+1,且i≠L.
(2)以重心点V(S+1)(H)为基本点,沿着最差点V(L)到重心点方向反射延长到反射点V(S+2)(H),计算反射点V(S+2)(FS)坐标及对应的函数f(V(S+2)(FS)).
V(S+2)(FS)=V(s+1)(H)+(V(S+1)(H)-V(L))=
2V(S+1)(H)-V(L).
若f(V(S+2)(FS))>f(V(H),则执行扩张运算;
若f(V(L)) 若f(V(S+2)(FS)) 扩张运算: V(S+2)(KZ)=V(S+1)(H)+ γ(V(S+2)(FS)-V(L)),γ=1.2~2.5. 若f(V(S+2)(KZ))>f(V(S+2)(FS)),以扩张点V(S+2)(KZ)代替最差点V(L)构造新的单纯形;否则扩张不成功,以反射点V(S+2)(FS)代替最差点V(L)构造新的单纯形,转入Setp2中继续最优搜素,直至满足收敛条件. 收缩运算: V(S+2)(SS)=V(S+1)(H)+ δ(V(S+2)(FS)-V(S+1)(H)),δ=0~1. 以收缩点V(S+2)(SS)代替最差点V(L),构造新的单纯形转入Setp2中进行最优搜索,直至满足收敛条件. 压缩运算: V(S+2)(YS)=V(S+1)(H)+ η(V(L)-V(S+1)(H)),η=0~1. 以压缩点V(S+2)(YS)代替最差点V(L),构成新的单纯形转入Setp2中进行最优搜索,直至满足收敛条件. Step4若经过有限N次迭代之后,仍不能满足收敛,证明最优搜索方向有误,需要以次最差点V(G)和去除次最差点后的重心V(S+1)(G)为基本点进行搜索,然后重复Setp2,直至满足收敛条件. 图2 仿真设计流程图Fig.2 The flow chart of simulation design 本文借助于MATLAB软件中的GUI设计模块制作单纯形最优搜索界面.本界面中函数表达式采用inline函数的书写格式,同时本界面只适用于最大结果的搜索,针对具有极小值的函数可通过函数改造使其变为求极大值,仿真界面见图3 . 图3 单纯形寻优仿真GUI界面Fig.3 The simulation GUI interface about simplex optimization 为了验证本文算法的正确性和有效性,通过对四个包括单峰、多峰、低纬、高维的测试函数进行仿真来验证可视化界面及寻优效果,测试用函数介绍如下: 函数1简单函数:y=-(x1-1)2-(x2-1)2,x∈[-10,10],该函数为单峰函数,该函数在x=(1,1)取得全局最优,且最优值y(max)=0. 函数2改造的Beale函数,由于该函数在自变量区间[-10,10]内存在极小值,为了适应于本可视化界面,将其改造后变为寻极大值,改造后的函数在x=(3,0.5)存在极大值,且最优值y(max)=0,该函数的表达式为: y=-(1.5-x1(1-x2))2- (2.25-x1(1-x22))2- (2.625-x1(1-x23))2, x∈[-4.5,4.5] . 函数3改造的多峰Six Hump Camel back函数,经改造后该函数在区间[-5,5]有六个极大值峰,且在x=(0.0898,-0.7126)处有极大值,且最优值y(max)=1.0316,该函数表达式为 x1x2+4x22-4x24, x∈[-5,5]. 函数4改造的Colville 函数,经改造后该函数在区间[-10,10]存在极大值,且在x=(1,1,1,1)极大值为y(max)=0,该函数表达式为: y=-100(x2-x12)2-(1-x1)2- 90(x4-x32)2-(1-x3)- 10.1[(x2-1)2+(x4-1)2]- 19.8(x2-1)(x4-1)2, x∈[-10,10]. 为了直观观察函数的极值个数,本文借助于MATLAB中mesh函数,以0.02为步长,制作了测试函数1、测试函数2及测试函数3的三维图见图4、图5及图6,从三图可知三函数在搜索区间内均存在极大值,满足测试要求. 图4 简单函数三维图Fig.4 The 3D graph of simple function 图5 改造Beale函数三维图 Fig.5 The 3D graph of transform Beale function 图6 改造 Six Hump Camel back函数三维图 Fig.6 The 3D graph of transform Six Hump Camel back function 对以上函数将相关参数输入图3中的GUI界面,经过后台运算输出相关参数见表1及寻优轨迹见图7至图10.从表1中可知本程序的寻优结果与实际的最优结果均较为接近,从图7至图10可以发现随着迭代次数的延长(100次)寻优结果均有向最优结果靠近的趋势,证明该可视化界面能适用于一般函数寻优,从迭代次数上来看,对于单纯形寻优搜索,其收敛速度具有一定的优势. 图7 简单函数寻优轨迹图Fig.7 The optimization track map about simple function 图8 改造Beale函数寻优轨迹图Fig.8 The optimization track map about transform Beale function 表1 函数输入及输出参数 函数初始顶点最优顶点寻优结果实际最优最优迭代次数函数10,00.98191,0.98191-0.0006544022函数21,12.9274,0.4879-0.0018046函数33,30.0843,-0.6691491.01721.031645函数43,3,3,30.9921,0.9985,0.9937,0.9933-0.0138075 图9 改造Six Hump Camel back函数寻优轨迹图Fig.9 The optimization track map about transform Six Hump Camel back function 图10 改造的Colville 函数寻优轨迹图Fig.10 The optimization track map about transform Colville function 寻优算法的改进、应用及多种算法的融合属于近几年研究的热点,其中对于单纯形的研究主要集中在应用及与其他算法的融合寻优两个方面,对于该算法的可视化仿真的研究较少.本研究利用MATLAB软件设计开发改进单纯形的可视化仿真平台,使该寻优方法的使用及运行过程更加直观、易实现.后续研究主要借助于MATLAB软件中的Mbuild-setup函数,结合实际应用,开发改进单纯形寻优可视化的独立运行程序,使其使用更方便. [1]刘建文,丁洁玉,潘坤,等.基于个体相似度的改进自适应遗传算法研究[J].青岛大学学报(工程技术版),2016,31(1):16-19. [2]谢云.模拟退火算法综述[J].计算机应用研究,1999(5):7-9. [3]袁亚搏,刘羿,吴斌.改进蚁群算法求解最短路径问题[J]. 计算机工程与应用,2016,52(6):8-12. [4]刘华蓥,林玉娥,张君施. 基于混沌搜索解决早熟收敛的混合粒子群算法[J].计算机工程与应用,2006(13):77-79. [5]王辉.人工神经网络研究与发展综述[J].电脑知识与技术,2008,4(3):710-711. [6]孔锐睿,仇汝臣,周田惠.单纯形的加速算法[J].南京理工大学学报,2003,27(2):209-231. [7]SPLENDLEY W, HEXT G R, HIMSWORTH F R. Seqauential application of simplex designs in optim ization and evolutinary operation[J] .Technometrics, 1962(4): 441- 461. [8]NELDER J A, MEAD R. A simplex method for function minimization[J] . Computer J, 1965, 7: 308- 313. [9]肖宏峰,谭冠政.单纯形搜索在遗传算法中的融合研究[J].计算机工程与应用,2008,44(18):30-33. [10]宋星原,舒全英,王海波,等.SCE-UA、遗传算法和单纯形优化算法的应用[J].武汉大学学报(工学版),2009,42(1):6-9,15. [11]杜修力,崔冬,侯本伟.基于初始群改进策略的经验遗传-单纯形法[J].北京工业大学学报,2014,40(12):1876-1883. [12]张佳程,周邵萍,苏永升,等.基于数据融合与单纯形遗传算法的管道损伤识别[J].华东理工大学学报(自然科学版),2015,41(1):132-136. [13]谢学斌,罗海霞,杨承祥,等.基于遗传单纯形算法与RBF网络的地应力场反演方法[J].铁道科学与工程学报,2015,12(1):72-78. [14]张红霞,罗毅,师瑞峰.基于单纯形法的改进型人工鱼群算法[J].计算机应用,2011,31(5):1321-1323,1327. [15]彭培真,俞毅,王兆嘉,等.基于单纯形的改进全局人工鱼群优化算法[J].计算机技术与发展,2015,25(8):75-79. [16]任小康,郝瑞芝,孙正兴,等.基于单纯形法的量子粒子群优化算法[J].微电子学与计算机,2010,27(1):154-157. [17]郑伟博,张纪会.基于Nelder-Mead单纯形法的改进量子行为粒子群算法[J].复杂系统与复杂科学,2016,13(2):97-104. [18]肖辉辉.基于单纯形法和自适应步长的花朵授粉算法[J].计算机工程与科学,2016,38(10):2126-2133. [19]欧阳艾嘉,张伟伟,周永权.单纯形和人口迁移的混合全局优化算法[J].计算机工程与应用,2010,46(4):29-31,35. [20]胡德庚,朱云勤,王朝军,等.基于单纯形的硅钙钾肥制备工艺研究[J].化学工业与工程,2013,30(3):55-59. [21]钮琰星,倪光远,万楚筠,等.基于单纯形-中心设计的菜籽粕生物改良菌株的复配研究[J].中国油脂,2015,40(2):72-76. [22]杨树朝.基于单纯形法的重介密度控制系统PID自寻最优控制的设计[J].选煤技术,2016,(1):81-83. [23]聂强,何仁,黄永春,等.单纯形重心法优化西番莲果汁饮料的稳定剂配方[J].安徽农业科学,2016,44(9):109-111,188. [24]何慧蓉,陈际达,陈世金,等.单纯形化法研究改良型全加成PCB的铜电镀液配方[J].电镀与涂饰,2016,35(13):677-680. [25]李士森,裴俊红.MATLAB在运筹学(单纯形法)教学中的应用[J].石家庄铁路职业技术学院学报,2009,8(3):108-111. [26]张丽平,李林,李松,等.预定数据链规模的单纯型连续近邻链查询[J].计算机工程,2012,38(10):51-53. [27]张丽平,李松,赵纪桥,等.受限区域内的单纯型连续近邻查询方法[J].计算机应用,2014,34(2):406-410. [28]李松,张丽平,刘艳等.障碍物环境下的动态单纯型连续近邻查询[J].计算机工程,2014,40(8):52-57. [29]李松,张丽平,朱德龙,等.动态受限区域内的单纯型连续近邻链查询方法[J].计算机科学,2014,41(6):136-141. [30]熊沛石.初始单纯形的构造方法[J].湖南有色金属,1986,2(6):42-46.2 可视化仿真界面的设计
2.1 设计流程(图2)
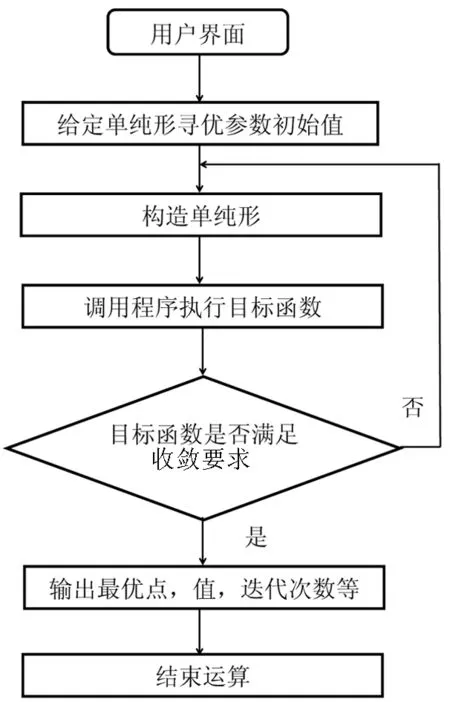
2.2 可视化界面

3 仿真训练
3.1 测试函数
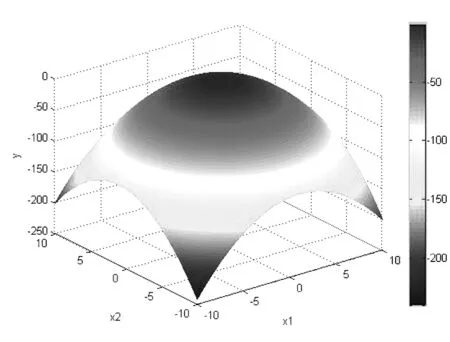
3.2 测试训练效果
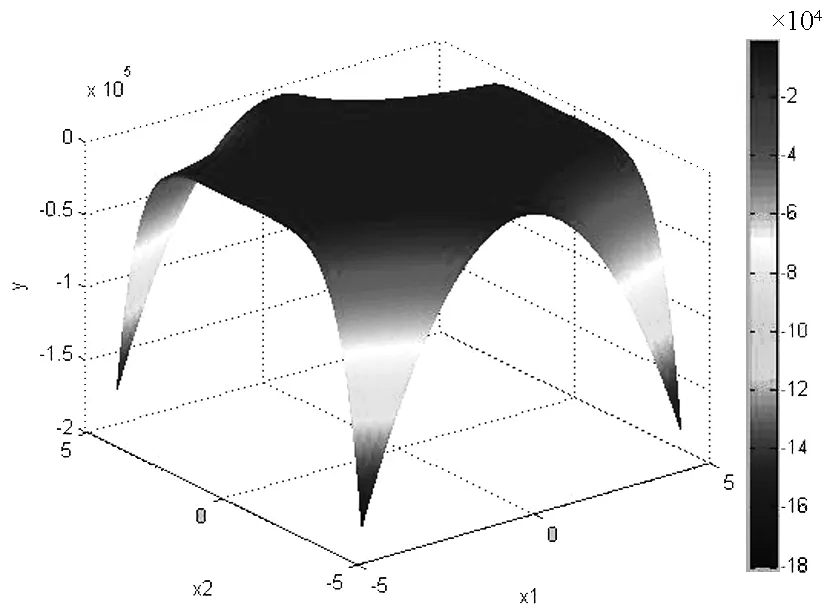

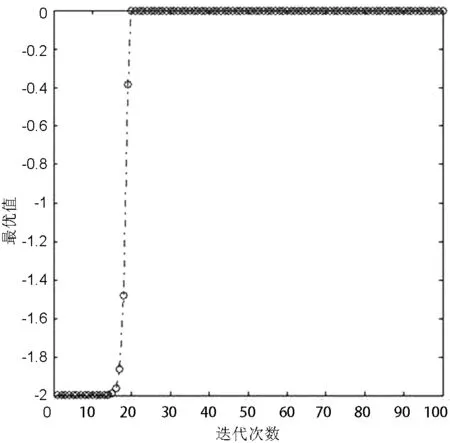
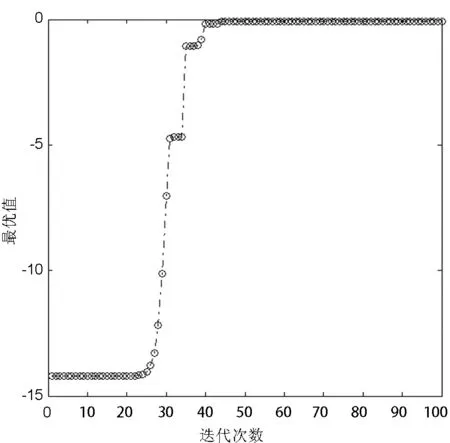
Tab.1 The input and output parameters about function
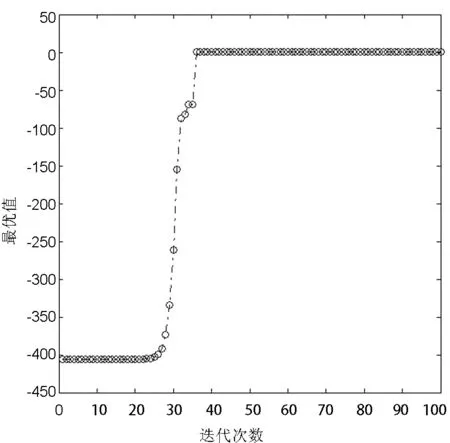
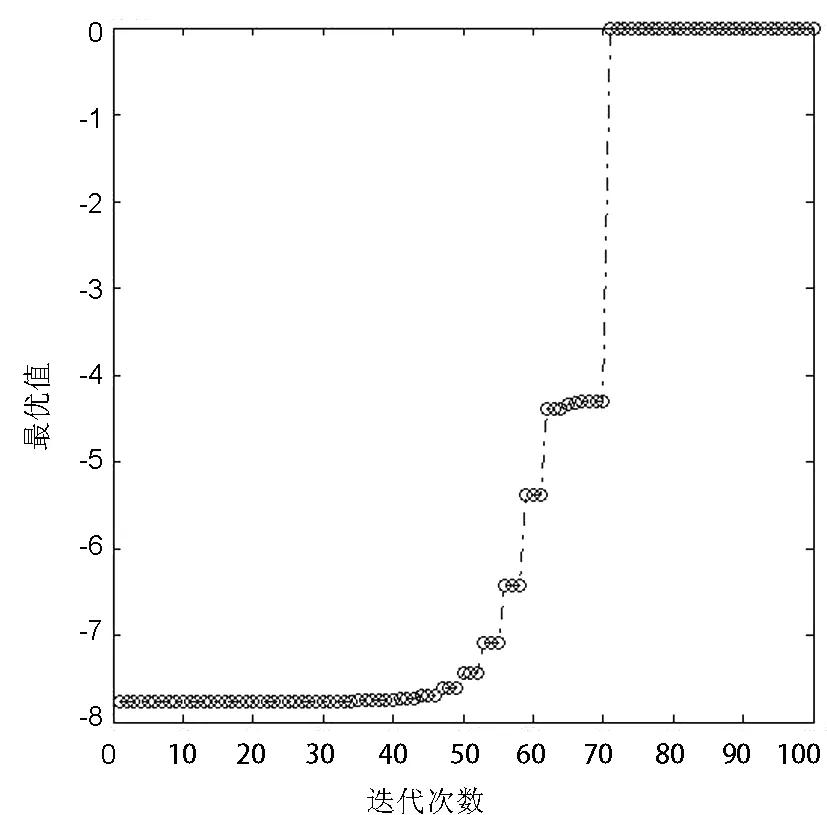
4 结束语

