高超声速飞行器分解集成轨迹预测算法
韩春耀, 熊家军, 张 凯, 兰旭辉
(空军预警学院预警情报系, 湖北 武汉 430019)
0 引 言
临近空间高超声速飞行器突防能力强、打击精度高、硬目标摧毁能力强,这些特点使得临近空间高超声速飞行器受到各军事强国广泛关注。作为防御方,研究临近空间高超声速飞行器的轨迹预测问题,一方面有助于预警探测网络高效地管理探测资源,保持连续跟踪目标;另一方面有助于制定拦截作战方案,对于防御该类目标具有重要意义。
目前,关于临近空间高超声速飞行器轨迹预测的参考文献还较少。临近空间高超声速飞行器本质上是一种升力式再入飞行器,根据采用发射平台类型,可分为无动力滑翔高超声速飞行器(如AHW、HTV-2、CAV-H)、吸气式巡航高超声速飞行器(如X-51A)和空天往返飞行器或者称为亚轨道飞行器(如X-37B)。关于该类目标的轨迹预测研究大多集中在预测制导领域,但制导是从进攻方视角实施轨迹预测,能够获取更多、更准确的先验知识[1-5]。现主要从防御的视角研究无动力滑翔高超声速飞行器的轨迹预测问题。
实现轨迹预测的前提是目标运动符合一定规律,随机的机动无法实现有效的预测。文献[6-7]认为轨迹预测的关键是获得飞行器的升阻比,认为再入拉起后飞行器升阻比线性增加且升阻比是关于运动状态的函数,通过函数拟合计算升阻比关于时间的函数,在此基础上通过数值积分预测运动轨迹。文献[8]根据跟踪滤波结果计算飞行器当前时刻的控制参数,通过运动微分方程数值积分预测飞行轨迹。上述方法均基于目标的动力学方程并通过数值积分外推飞行轨迹,数值积分法能够综合影响飞行器轨迹的各种因素[9],在能够获得高精度的初始状态以及控制量估计值的条件下,具有较高的轨迹预测精度。文献[10-11]研究了无动力高超声速滑翔飞行器的弹道特征,分析了再入初始状态对弹道的影响,认为基于动力学方程的轨迹预测方法对方程中的未知参数以及初始状态均敏感。因此,基于动力学方程的轨迹预测方法对目标状态初值以及系统参数估计具有较高要求,这将制约这类方法的运用。
文献[12]利用广义回归神经网络(generalized regression neural network, GRNN)预测高超声速飞行器轨迹,其实质是利用径向基函数逼近非线性运动方程,进而外推飞行轨迹。运用神经网络轨迹预测的方法受制于训练样本规模,在获得少量测数据的条件下,该方法预测精度低。文献[13]研究了零倾侧角条件下无动力滑翔高超声速飞行器的轨迹预测问题,先利用交互式多模型估计目标状态,再用双正弦和函数拟合目标的加速度曲线,最后用状态估计值作为状态初值外推轨迹。该方法假设探测器具有较高的探测精度,轨迹预测的精度取决于运动状态的估计精度。
为了解决上述问题,试图从历史轨迹中挖掘运动轨迹的特征,借鉴分解集成的思路,将飞行器运动轨迹序列分解为具有不同特征的子序列,根据子序列的特征建立相应的预测模型,将各子模型预测结果的集成作为最终的轨迹预测结果。
1 轨迹可预测性分析
无动力滑翔高超声速飞行器的控制量根据制导律不断变化,这增加了轨迹预测的难度,但也有规律可循。为了减小控制系统复杂度,控制量常遵循一些规律,如攻角设计为速度的分段线性函数[14-15],倾侧角按照分段常值和符号翻转规律设计,这都为飞行器轨迹预测提供了可能。将针对无动力滑翔高超声速飞行器在滑翔段的轨迹预测问题,研究常攻角条件下的滑翔段轨迹预测方法。
飞行器在滑翔段飞行时间最长,具有较长的拦截窗口,且运动轨迹相对平稳,机动能力有限,无欺骗式干扰,易于连续跟踪并便于拦截[16],因而考虑滑翔段轨迹预测。根据无动力滑翔高超声速飞行器滑翔段轨迹优化结果,为达到最大纵程飞行器需要保持较大升阻比。升阻比的大小与飞行器攻角以及速度有关,其中攻角是主要因素,CAV-H升阻比与攻角的关系曲线类似非对称的钟罩,并在10°~15°达到最大[17]。文献[2]认为在飞行器再入拉起后,采用最大升阻比滑翔轨迹与以最大纵程为优化目标的优化轨迹是一致的,并且接近拟平衡滑翔结果。因此,无动力滑翔高超声速飞行器在滑翔段为获得最大射程,常保持较大升阻比,即攻角接近线性变化且变化量小,研究常攻角条件下的滑翔段轨迹预测是合理的。
2 分解集成轨迹预测算法
在时序混合模型研究领域,文献[18-19]针对复杂系统提出了TEI@I(text mining, econometrics, intelligence, integration)方法论,该方法论的核心是先分解再集成,将文本挖掘、传统计量、人工智能以及系统集成等技术相融合,以发挥各模型的长处避免其不足,最终达到提高预测精度的目的。无动力滑翔高超声速飞行器在滑翔段的飞行轨迹表现出明显的周期性运动和趋势性,分解集成轨迹预测算法采用该思想,将运动轨迹表现出的明显的周期性和趋势性规律分离,针对不同的轨迹变化规律设计相应的子轨迹预测模型,从而提高预测模型的拟合精度和降低预测模型的运算量。
2.1 分解集成轨迹预测原理
分解集成轨迹预测模型利用函数变换将运动轨迹分解为趋势项、周期项以及随机项,再通过加法模型或者是乘法模型生成最终的轨迹预测模型。将采用加法模型,加法模型可以通过指数变换转化为乘法模型。
假设飞行器轨迹序列表示为x,并采用加法模型,则轨迹序列可以分解为
x=[x(1),x(2), …,x(n)]=T+S+I
(1)
其中
T=[xT(1),xT(2), …,xT(n)]
S=[xS(1),xS(2), …,xS(n)]
I=[xI(1),xI(2), …,xI(n)]
式中,T表示轨迹的趋势项,反映了轨迹在长时间尺度上表现的运动趋势;S表示轨迹的周期项,反映了轨迹重复变化规律;I表示随机项,反映了不确定性因素引起的位置变化。
将轨迹序列分解为具有趋势、周期以及随机特性的子序列,针对子序列的特性选择相应的子轨迹预测模型并分别预测T、S、I,则轨迹预测模型的最终输出为
(2)
2.2 轨迹序列分解方法
分解集成轨迹预测算法的首要步骤是将轨迹序列分解。信号处理领域常用的分解方法有傅里叶分解、小波分解、经验模态分解(empirical mode decomposition, EMD)[20],还有EMD的改进集成经验模态分解(ensemble EMD, EEMD)[21]。将轨迹序列看作离散信号,利用分解方法将原轨迹序列分解。文献[20]提出了EMD算法,该算法适用于分析非线性、非平稳时间序列,抗噪声能力强,并且EMD算法不需要事先确定基函数,与基于小波基函数的小波分解和基于谐波基函数的傅里叶分解不同,能够根据序列的时间尺度自适应的确定特征。EMD算法能够将轨迹序列分解为有限个本征函数(intrinsic mode function, IMF),实际表现形式为处理后的序列,而并非归纳为与谐波基函数类似的函数形式。
在应用中,EMD算法存在模态混淆的现象,导致轨迹序列变化规律分解不清晰。文献[21]基于EMD提出了集成经验模态分解。EEMD的基本思想是在原始时间序列叠加高斯白噪声基础上多次运行EMD。
EEMD算法的实现过程如下:
步骤1程序参数初始化。设置EMD的运行次数为K,白噪声的幅值系数为ε,令运行次数计数器k=1。
步骤2执行第k次EMD算法。在轨迹序列x上叠加高斯白噪声序列Gk,生成第k次待分解的时间序列xk。需要注意,每次在原时间序列上叠加的高斯白噪声序列要满足高斯同分布并且相互独立,以达到在多次输出平均后抑制或者消除噪声的目的。生成的待分解时间序列表示为
xk=x+ε·Gk
(3)
式中,ε为叠加的高斯白噪声的幅值系数。
执行EMD算法,得到轨迹序列的D个分量,并且将分解残余项看作最后一个分量。
(4)
式中,Cd,k为第k次EMD分解的第d个分量;RD,k表示残余项。
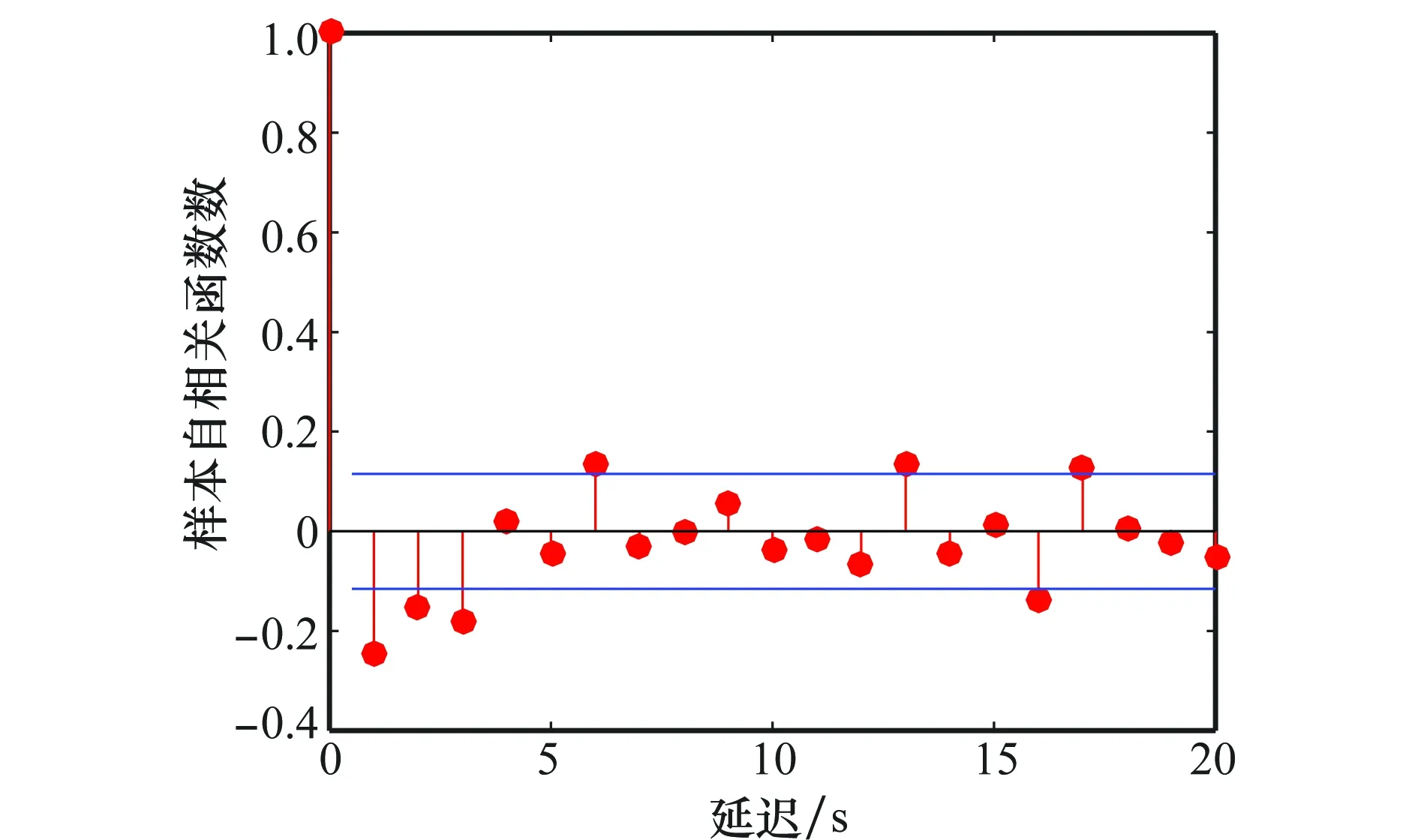
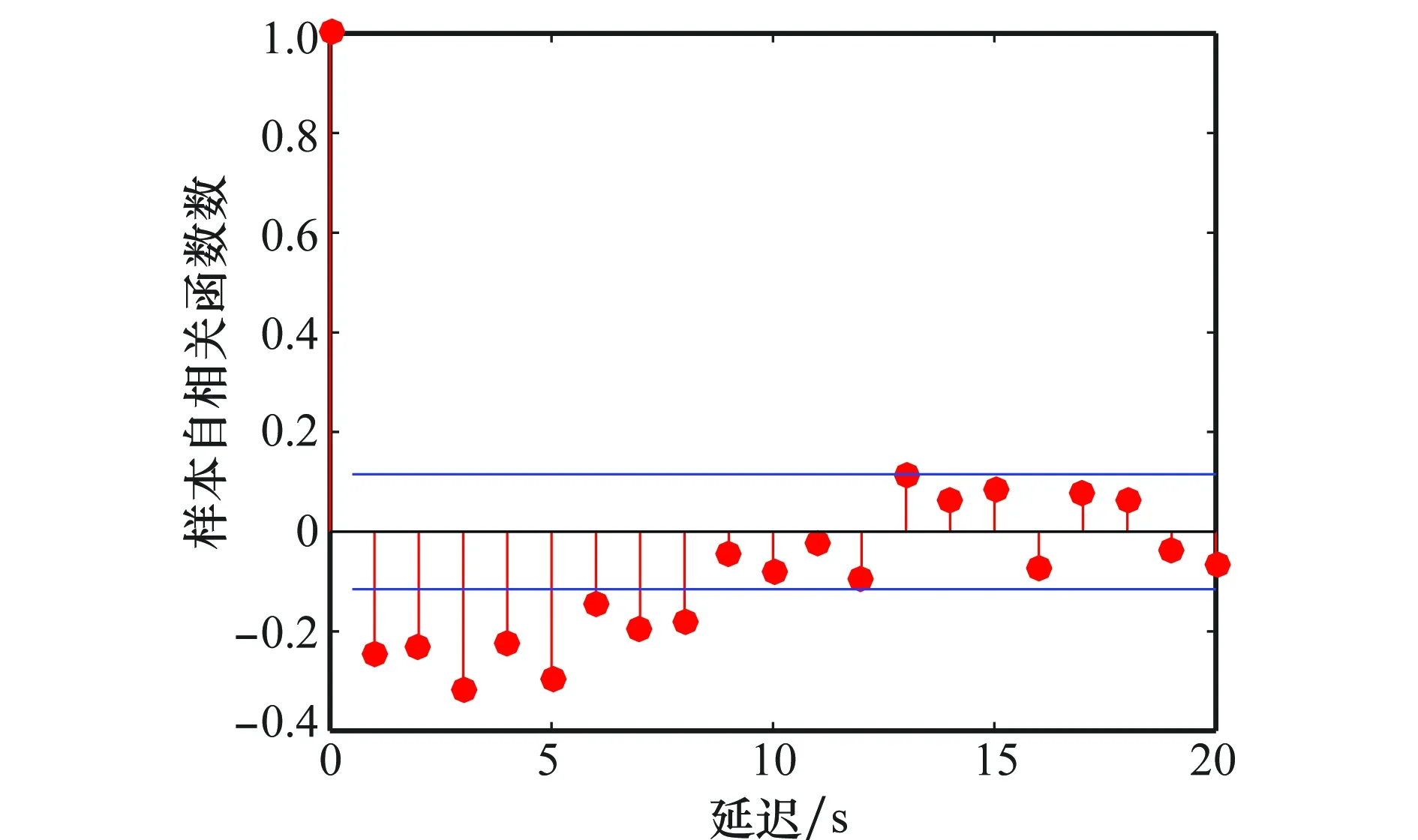
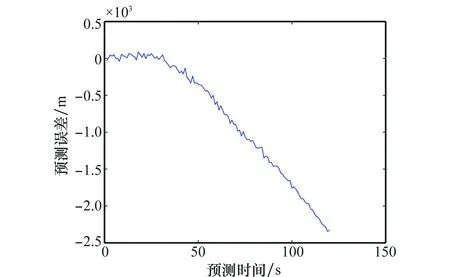
如果k 步骤3根据K次EMD算法的输出均值确定最终的分解结果。 (5) 将轨迹时间序列分解后,再利用傅里叶变换分析时间序列的频谱结构和相位信息。最后根据频谱分析结果,整合具有相同或者相似频谱结构的IMF,构造飞行轨迹时间序列的子序列T、S、I。趋势项T包含的是低频部分,其中IMF个数为dT;周期项S包含的是频率在1/P附近的IMF,包含dS个IMF;其余部分为随机项I,包含dI个IMF。轨迹序列分解后的各个项表示为 (6) 图1为轨迹序列分解的结果。通过分析EEMD分解结果的频谱结构,将无明显主频率的IMF合并作为随机项,将有明显主频率的IMF合并作为周期项,残余项作为趋势项。由于趋势项具有较高的能量,因此与原始轨迹序列具有类似的频谱。分解集成轨迹预测模型采用批处理方式,即根据某一时间段内目标状态的滤波结果预测目标轨迹。求解预测模型参数利用的轨迹序列的集合称为训练集,训练集中包含的样本的个数称为训练样本容量,从轨迹序列分解的流程看,为分解出周期项,训练样本容量应大于运动周期。 图1 轨迹序列分解结果Fig.1 Trajectory sequence decomposition results 轨迹序列分解后,针对子序列的特征选择合适的子轨迹预测模型,模型选取考虑的因素有模型与运动规律的拟合程度、训练集容量以及时效性等。分解集成轨迹预测根据训练样本预测目标未来运动状态,子模型选取基于统计模型和神经网络模型。统计模型用随机性的方程描述序列内部要素间的定量关系,常见统计模型有自回归(auto regressive, AR)模型、滑动平均(moving average, MA)模型、自回归滑动平均(auto regressive moving average, ARMA)模型、自回归积分滑动平均(auto regressive integrated moving average, ARIMA)模型、自回归条件异方差(auto regressive conditional heteroscedastic, ARCH)模型等,其中前3种模型可以看做ARIMA模型的特例。神经网络模型利用机器学习拟合输入状态至预测状态的非线性映射,主要考虑支持向量回归模型以及神经网络模型。考虑的子模型集包含ARMA模型、最小二乘支持向量回归(least square support vector regression, LSSVR)模型以及误差反向传播神经网络(error back propagtion neural network, BPNN)模型。 轨迹序列分解的随机项建模为ARMA模型,表示为 Yn=φ1Yn-1+φ2Yn-2+…+φpYn-p+ en-θ1en-1-θ2en-2-…-θqen-q (7) 式中,p和q为模型阶数。建模时首先检验轨迹序列平稳性,再确定预测模型参数,最后模型检验。平稳性检验可以根据序列的波形特征判断,也可构建检验统计量进行假设检验。利用KPSS(Kwiatkowski、Phillips、Schmidt、Shin)检验判断其平稳性,随机项是平稳的。随机项的自相关函数(auto-correlation function,ACF)数与偏自相关函数(partial ACF,PACF)数如图2和图3所示,均为峰值后拖尾衰减,因此模型形式为ARMA(p,q)。其中,p最大为3,q最大为8,因此共有24种模型,利用贝叶斯信息准则(Bayesian information criterion, BIC)评价统计模型的拟合优良性,最优p选为3,最优q选为2。BIC模型表示为 BIC=-2log2(L)+klog2(N) (8) 式中,L为极大似然估计;N为训练样本容量;k相当于惩罚函数,确保选择简洁模型,避免模型输入参数太多。若模型包含截距和常数项,则k=p+q+1;否则k=p+q。 图2 随机项的自相关函数数Fig.2 ACF of random item 图3 随机项的偏自相关函数数Fig.3 PACF of random item 轨迹序列分解的周期项选择非线性映射能力强的模型,备选模型为LSSVR模型和BPNN模型。考虑到轨迹预测能够使用的历史数据有限,而LSSVR对于小样本的回归性能具有优势,并且具有优化速度快、运算复杂度低等特点,周期项建模为LSSVR模型。 y=ωTφ(x)+b (9) 式中,φ(·)表示非线性映射函数,将样本从原始空间映射到一个更高维的特征空间(Rm→Rmf);ω∈Rmf是权向量;b是偏置量。 最小二乘支持向量回归的目标函数为 s.t.yi=ωTφ(xi)+b+ei,i=1,2,…,N (10) 利用拉格朗日乘子法获得其对偶问题,最终获得LSSVR的非线性函数式,这里不再赘述求解过程,即回归机为 (11) 式中,k(x,xi)为核函数,选择径向基核函数;α为拉个朗日乘子。 轨迹序列分解的趋势项具有明显的线性特征,因此,趋势项建模为AR模型。 分解集成轨迹预测算法流程如下: 步骤1利用EEMD分解轨迹序列,将轨迹序列分解为趋势项、周期项以及随机项3个子序列,每个子序列具有不同的特征。 步骤2针对子序列的特征选取相应的轨迹预测模型外推子序列。 步骤3整合子轨迹预测模型的预测结果,获得最终的预测结果。 根据轨迹预测应用需求,预测飞行器未来60 s的运动轨迹,即实现多步预测。但子模型的预测结果为一步预测,采用迭代预测的方法实现多步预测。迭代预测将一步预测的估计值作为输入,通过多步一步预测实现多步预测。由于将预测值而不是量测值作为预测模型的输入,会导致误差的传播,造成累积误差。 通过对飞行器再入过程运动微分方程进行Runge-Kutta数值积分,获得仿真所需的飞行器轨迹数据。飞行器的参数,如质量、气动参数等,参照美国洛克希德-马丁公司设计的高超声速飞行器CAV-H[22];飞行器的初始状态根据经验设置,速度为3 000~4 000 m/s,高度为40~60 km;控制量倾侧角设置为0°,即保证飞行轨迹在同一平面,只考虑目标的纵向机动,控制量攻角设置为10°~15°的常值,使飞行器保持常攻角飞行;轨迹预测的前提是连续跟踪目标,预警探测系统的采样周期为1 s,当采样周期为1 s时,训练样本容量与观测时间数值上相等,跟踪滤波均方根误差(root mean square error, RMSE)设置为50 m。图4为生成的一条无动力滑翔高超声速飞行器滑翔段模拟轨迹。 图4 无动力滑翔高超声速飞行器模拟轨迹Fig.4 Simulation trajectory of unpowered gliding hypersonic vehicle 为验证所提分解集成轨迹预测算法的性能,设计仿真对照实验。对照组采用BPNN模型、LSSVR模型以及ARIMA模型,其中前两种为基于机器学习的单模型,其中BPNN借助Matlab Neural Network Toolbox 8.2中的函数实现,LSSVR借助LIBSVM 3.21中的函数实现。BPNN模型、LSSVR模型均具有非线性映射能力,能够单独作为预测模型。ARIMA模型为统计模型,多应用于经济领域的短期预测,也可将轨迹序列建模为ARIMA模型实现轨迹预测。 轨迹预测算法的性能主要是指预测精度,评价指标采用均方根误差,表示为 (12) 根据轨迹预测性能的评价标准,对比分析迹预测算法的性能。设训练样本容量为300,轨迹预测时间为60 s,即根据飞行器前300 s的历史轨迹预测未来60 s的运动轨迹。表1为4种轨迹预测算法在不同预测时间的预测精度对比。图5为4种轨迹预测算法预测精度随时间的变化。图6为执行一次轨迹预测算法的预测效果演示。可见,提出的分解集成模型预测精度最高,预测60 s的RMSE为639 m,BPNN模型、LSSVM模型次之,ARIMA模型预测精度最低,预测60 s的RMSE为3 010 m。ARIMA模型的预测精度低的原因是ARIMA是典型的线性模型,不能通过训练样本反映轨迹的非线性特征和周期性特征。同时,随着预测时间的增加,所有预测模型的预测RMSE均增大。 表1 不同预测模型的预测精度 图5 轨迹预测精度随时间变化Fig.5 Prediction RMSE versus time 图6 不同预测模型时单次预测结果Fig.6 Prediction results of different models 为进一步研究影响分解集成轨迹预测算法精度的因素,分别分析训练样本容量和预测起点对预测精度的影响。图7为预测精度和训练样本容量的关系,展示了样本容量为300、240、180时预测精度随预测时间的变化。轨迹分解集成轨迹预测算法利用一段轨迹序列预测运动轨迹,但轨迹序列要大于运动周期时,才能准确地分解出周期项,进而提高预测精度。仿真结果与验证了分析结果,随训练样本容量的增加,轨迹预测精度显著提高。图8为轨迹预测的一次示例,训练样本容量为180时,小于运动轨迹的周期,大约为200 s,从而轨迹预测模型不能准确刻画周期特征,导致预测精度急剧下降。 图7 预测精度与训练样本容量的关系Fig.7 Relationship between sample size and prediction precision 图8 不同样本容量时的单次预测结果Fig.8 Prediction results of different sample sizes 图9为预测精度与预测起点的关系。当预测起点靠近轨迹的波峰或者波谷时,如预测起点为300 s或370 s时,轨迹预测精度约为1.5 km,而预测起点在两者之间时,预测精度为0.8 km,因此,预测起点影响预测精度。在高超声速飞行器单个运动周期内,在不同的位置的机动能力有差异,例如在轨迹的波峰或者波谷时加速度变化快,而在中间过程加速度缓慢变化,仿真结果验证了飞行机动能力弱时降低了预测难度,有助于提高轨迹预测的精度。图10为不同预测起点时的单次预测结果。 图9 预测精度与预测起点的关系Fig.9 Relationship between prediction precision andprediction starting point 图10 不同预测起点时的单次预测结果Fig.10 Prediction results of different prediction starting points 为了展示提出的分解集成轨迹预测模型的预测性能,从320 s开始外推目标120 s的运动轨迹。将20~320 s总共300 s的滤波数据作为训练样本,分解集成轨迹预测模型的预测输出如图11所示。 图11 分解集成预测模型的单次预测结果Fig.11 Prediction results of decomposition ensembleprediction model 图12为一次仿真的预测误差。进行较长时间的轨迹预测有利于预警探测系统连续跟踪来袭目标、为组织实施拦截提供更长的准备时间,这也是进行轨迹预测目的。从预测效果可见,分解集成轨迹预测算法能够反映飞行器轨迹周期性波动和飞行高度呈下降趋势的特征。无动力滑翔高超声速飞行器采用高升阻比的气动外形,由高向低滑翔时,空气密度逐渐变大,所受重力将小于气动升力,产生向上加速度,由低向高滑翔时,随着飞行高度增加,空气密度逐渐变小,重力将大于气动升力,产生向下加速度,直至向上的速度为零后向下运动,以此往返运动,形成周期性波动特性。但飞行器的能量逐渐减小,飞行高度表现出逐渐减低的趋势。提出的分解集成轨迹轨迹预测模型,轨迹序列分解的周期项与趋势项与上述运动规律相符合,因此具有良好的轨迹预测效果。 图12 单次轨迹预测的预测误差Fig.12 Prediction error of single performance 针对无动力滑翔高超声速飞行器轨迹预测问题,提出了分解集成轨迹预测算法。通过仿真实验得出以下结论:分解集成轨迹预测模型与其他轨迹预测模型相比,能够有效地提高轨迹预测精度。预测的时间越短轨迹预测的精度越高,这也说明由于不确定因素,实现长时间尺度的轨迹预测将十分困难。非线性模型比线性模型能够更好地拟合周期性变化规律。分解集成轨迹预测算法不仅预测时间灵活,既可以单步预测,也能够多步预测,而且可以应用于具有周期性变化规律的序列预测,具有较强的适用性。分解集成轨迹预测算法利用飞行器在较长时间内的运动轨迹特征预测未来状态,预测精度与训练样本容量和预测起始位置相关,在提高轨迹预测精度的同时,限制了轨迹预测的条件。 [1] ZHANG Z, HU J. Prediction-based guidance algorithm for high-lift reentry vehicles[J]. Science China, 2011, 54(3): 498-510. [2] YU W, CHEN W. Guidance scheme for glide range maximization of a hypersonic vehicle[C]∥Proc.of the AIAA Guidance Navigation and Control Conference, 2011: 6714. [3] HALBE O, MATHAVARAJ S, PADHI R. Energy based suboptimal reentry guidance of a reusable launch vehicle using model predictive static programming[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2010: 8311. [4] XU M L, CHEN K J, LIU L H, et al. Quasi-equilibrium glide adaptive guidance for hypersonic vehicles[J]. Science China Technological Sciences, 2012, 55(3): 856-866. [5] LU P, FORBES S, BALDWIN M. Gliding guidance for high L/D hypersonic vehicle[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2013. [6] 王路,邢清华,毛艺帆.基于升阻比变化规律的再入高超声速滑翔飞行器轨迹预测算法[J].系统工程与电子技术,2015,37(10): 2335-2340. WANG L, XING Q H, MAO Y F. Trajectory prediction of reentry hypersonic glide vehicle based on changing rule of lift-drag ratio[J]. Systems Engineering and Eletronics, 2015, 37(10): 2335-2340. [7] 王路,邢清华,毛艺帆.助推-滑翔无动力跳跃飞行器轨迹预测[J].空军工程大学学报(自然科学版),2015,16(1): 24-27. WANG L, XING Q H, MAO Y F. A track forecasting algorithm of boost-glide unpropulsive skipping vehicle[J]. Journal of Air Force Engineer University (Natural Science Edition), 2015, 16(1): 24-27. [8] 秦雷, 李君龙, 周荻. 临近空间非弹道式目标HTV-2跟踪滤波与预报问题[J]. 航天控制, 2015, 33(2): 56-61. QIN L, LI J L, ZHOU D. The problems of tracking filter and prediction for non-ballistic target HTV-2 in the near space[J]. Aerospace Control, 2015, 33(2): 56-61. [9] LI X R, JILKOV V P. Survey of maneuvering target tracking. Part II: motion models of ballistic and space targets[J]. IEEE Trans.on Aerospace and Electronic Systems, 2010, 46(1): 96-119. [10] 陈小庆,侯中喜,刘建霞.高超声速滑翔飞行器弹道特性分析[J].导弹与航天运载技术,2011,312(2):5-9. CHEN X Q, HOU Z X, LIU J X. Trajectory characteristic of hypersonic gliding vehicle[J]. Missiles and Space Vehicles, 2011, 312(2): 5-9. [11] 李广华, 张洪波, 汤国建. 高超声速滑翔飞行器典型弹道特性分析[J]. 宇航学报, 2015, 36(4): 397-403. LI G H, ZHANG H B, TANG G J. Typical trajectory characteristics of hypersonic glide vehicle[J]. Journal of Astronautics, 2015, 36(4): 397-403. [12] 杨彬, 贺正洪. 一种GRNN神经网络的高超声速飞行器轨迹预测方法[J]. 计算机应用与软件, 2015, 32(7): 239-243. YANG B, HE Z H. Hypersonic vechicle track prediction based on GRNN[J].Computer Applications and Software,2015,32(7): 239-243. [13] 魏喜庆, 王社阳, 李瑞康. 基于自适应IMM算法的高超声速飞行器轨迹预测[J]. 上海航天, 2016, 33(2): 27-31. WEI X Q, WANG S Y, LI R K. Trajectory prediction of hypersonic vehicle using adaptive interactive multiple model filter[J]. Aerospace Shanghai, 2016, 33(2): 27-31. [14] YAN X, WANG Z. Three-dimensional trajectory planning method for hypersonic glide vehicle[C]∥Proc.of the 18th AIAA/3AF International Space Planes and Hypersonic Systems and Techno-logies Conference, 2012. [15] 黄长强, 国海峰, 丁达理. 高超声速滑翔飞行器轨迹优化与制导综述[J]. 宇航学报. 2014, 35(4): 369-379. HUANG C Q, GUO H F, DING D L. A survey of trajectory optimization and guidance for hypersonic gliding vehicle[J]. Journal of Astronautics. 2014, 35(4): 369-379. [16] 刘超峰, 王谷, 张珍铭, 等. 临近空间高超声速目标防御技术需求分析[J]. 现代防御技术, 2015, 43(5): 18-26. LIU C F, WANG G, ZHANG Z M, et al. Technical requirements analysis of air denfense system intercepting fast attack weapons in near space[J]. Modern Defence Technology, 2015, 43(5): 18-26. [17] 孙勇,段广仁,张卯瑞,等.高超声速飞行器再入过程改进气动系数模型[J].系统工程与电子技术,2011,33(1):134-137. SUN Y, DUAN G R, ZHANG M R, et al. Modified aerodynamic coefficient models of hypersonic vehicle in reentry phase[J]. Systems Engineering and Electronics, 2011, 33(1): 134-137. [18] WANG S Y, YU L A, LAI K K. Crude oil price forecasting with TEI@I methodology[J]. Journal of Systems Sciences and Complexity, 2005, 18(2): 145-166. [19] YU L, WANG Z S, Tang L. A decomposition-ensemble model with data-characteristic-driven reconstruction for crude oil price forecasting[J]. Applied Energy, 2015, 156: 251-267. [20] HUANG N E, SHEN Z, LONG S R. The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis[C]∥Proc.of the Royal Society of London Series A, 1998: 903-995. [21] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2008, 1(1): 1-41. [22] PHILLIPS T H. A common aero vehicle (CAV) model, description, employment guide[R]. Schafer Corporation for AFRL and AF-SPC, 2003.
2.3 子轨迹预测模型选择
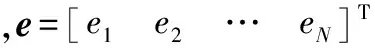
2.4 轨迹预测流程
3 实例分析
3.1 实验条件

3.2 实验设计

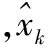
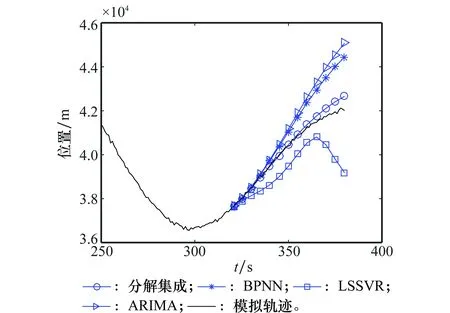
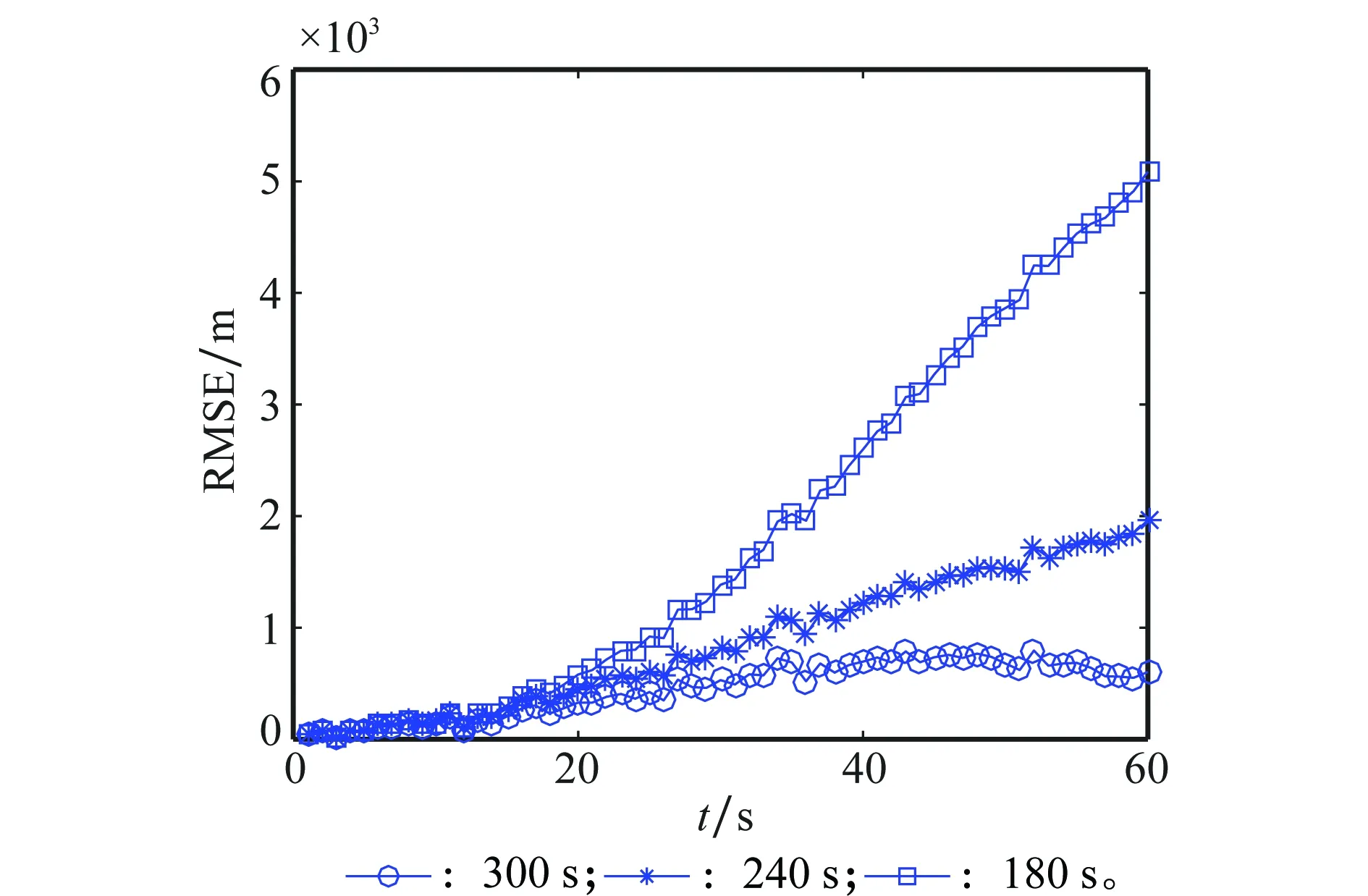
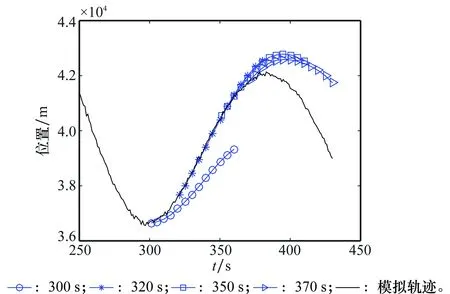
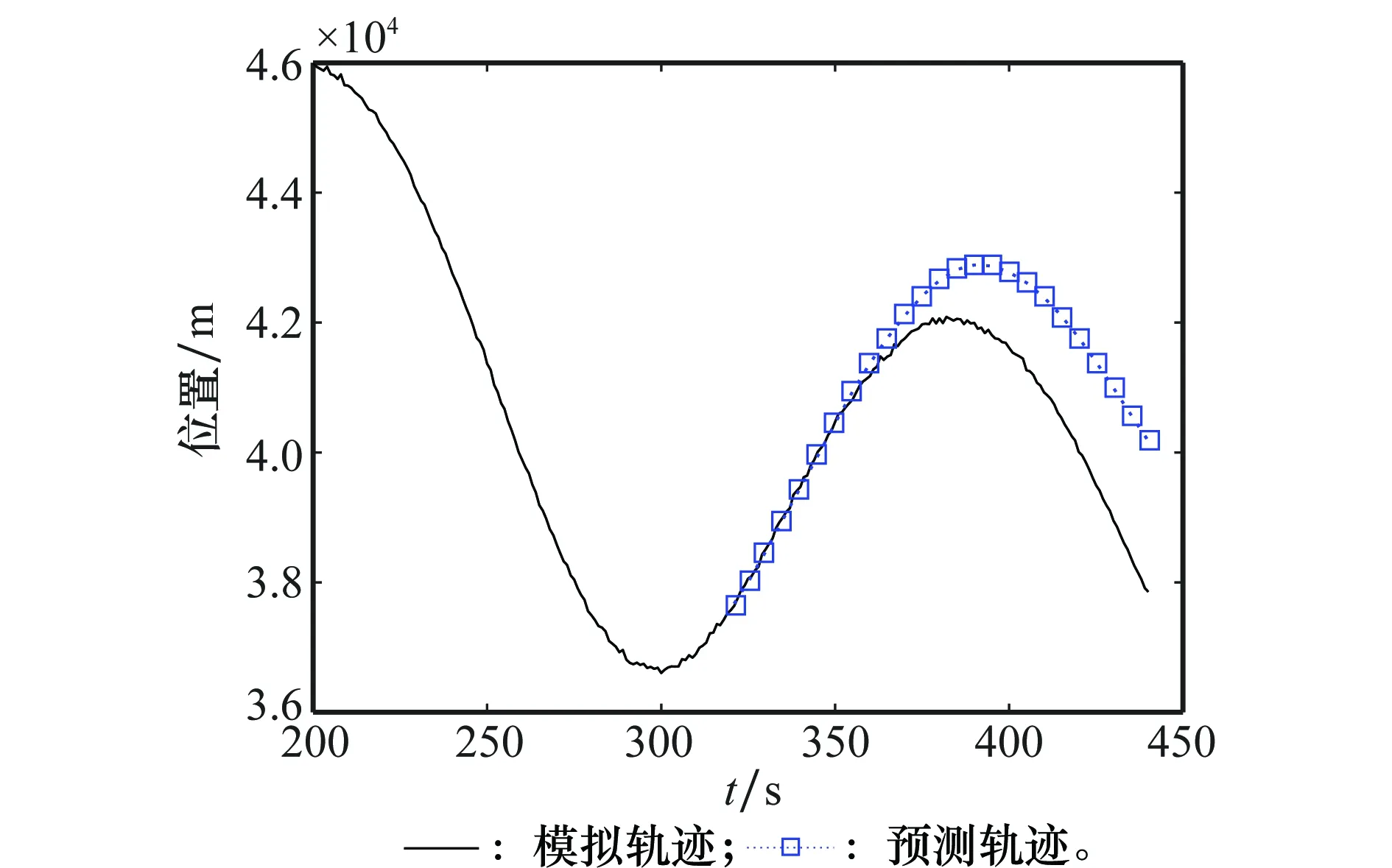
3.3 实验结果及分析




4 结束语

