基于滑模观测补偿的四旋翼飞行器鲁棒动态逆控制

陈 诚, 韦常柱, 琚啸哲, 刘鹏云

(1. 哈尔滨工业大学航天学院, 黑龙江 哈尔滨 150001; 2. 北京控制与电子技术研究所, 北京 100038)

0 引 言

四旋翼飞行器作为一种可垂直起降、空中悬停、成本低廉的旋翼飞行器,在军事、建筑、工业、商业等领域已经被广泛应用。但四旋翼飞行器模型难以精确建立,结构参数不确定性大,且具有强非线性、强耦合、欠驱动的系统特性,因此其飞行控制系统的设计具有一定难度[1]。

针对四旋翼飞行器,目前主要有3种控制策略:线性控制、非线性控制和智能控制。

线性控制策略即是基于小扰动线性化思想将四旋翼模型线性化处理,然后利用线性控制方法进行控制器设计。为克服模型本身欠驱动特性带来的控制困难,文献[2]将四旋翼飞行器进行位置、姿态双回路分层,对两回路分别进行PID控制器设计,并通过仿真验证了双回路PID控制的有效性。基于最优控制思想,文献[3-4]均利用线性二次型调节器(linear quadratic regulator,LQR)设计了姿态稳定控制器,能够实现飞行器姿态快速稳定控制和参考输入的快速跟踪。但是,线性控制设计过程中需要忽略模型中的耦合项以及非线性项,这将导致实际飞行中线性控制性能较差。

为应对四旋翼飞行器的非线性特性,反步法、滑模控制等非线性控制方法被应用到控制器设计中。文献[5]基于反步法设计了四旋翼飞行器的姿态跟踪控制器,并通过模糊监督规则在线选取控制参数,最后通过仿真证明了所设计控制器相较于线性控制方法具有更好的性能。文献[6]设计了H2/H∞控制器,通过求解线性矩阵不等式获取反馈控制律,并采用抗饱和算法提高了控制器的实用性。文献[7]考虑了四旋翼飞行器姿态控制系统欠驱动、强耦合的特性和非零初始误差的条件,设计了L1自适应控制器,能够保证在具有较大的结构参数不确定性时的高品质飞行性能,且具有较强的鲁棒性。上述非线性控制方法能够有效解决控制对象的非线性问题,但是或对模型精确度提出了较高要求,或无法同时考虑结构参数不确定性和外界干扰对飞行性能的影响,其在实际控制的具体应用中还需进一步深入研究。

为应对四旋翼飞行器模型的大不确定性可采用智能控制方法进行处理。目前研究较多的智能控制方法主要有神经网络控制和模糊控制。文献[8]针对四旋翼无人机的垂直起飞和降落控制问题,设计了一种模糊神经网络控制器能够使无人机能够在外部噪声、时变环境和不确定性下稳定飞行。文献[9-10]设计了改进的模糊控制方法,大幅缩短了四旋翼飞行器控制动态过程的稳定时间、超调量和振荡,提高了控制系统性能。智能控制方法的性能在一些特性上优于线性控制和非线性控制,但是其算法的计算量大,对飞控芯片性能的要求较高,目前还难以实现工程应用。

通过上述四旋翼飞行器控制策略的分析发现,非线性控制性能较好且工程应用具有一定的可行性,因此基于非线性控制方法进行四旋翼无人机的控制器设计。为实现在大参数不确定和外部扰动情况下的四旋翼飞行器鲁棒与高精度控制性能的兼顾,本文在经典双回路控制框架的基础上将新型针对不确定范数有界的鲁棒控制律与Super-twisting滑模控制算法相结合,构建了具备较强鲁棒性与抗扰性的四旋翼飞行器扩展鲁棒动态逆控制系统,具有扰动精确补偿、模型依赖性低、离线设计任务量小、实用性强等特点。

全文的安排如下：第1节中对四旋翼飞行器的结构和飞行原理进行简析并建立考虑不确定性的飞行动力学模型;第2节基于时标分离原则对动力学模型进行多回路分层,并基于Lyapunov理论给出鲁棒控制律以及该控制律的全局收敛性证明;第3节给出基于Super-twisting 算法的滑模干扰观测器的设计过程和观测原理论证;第4节对大结构不确定性和外部扰动情况下四旋翼飞行器进行仿真,以验证所设计的基于滑模观测补偿鲁棒动态逆控制的有效性。

1 四旋翼飞行器动力学建模

1.1 四旋翼飞行器结构和飞行原理简析

本文以图 1所示的四旋翼飞行器为研究对象,其重量和尺寸如表 1所示。该飞行器在结构上由起落架、基座(云台)、2根支架、4个直流无刷电动机、旋翼等部分组成。2根支架彼此正交,4个旋翼对称布置安装在2根支架上,并且与飞行器重心等距[11]。

图1 选用的四旋翼飞行器实体图Fig.1 Adopted quad-rotor unmanned vehicle

结构参数数据正常重量/kg1．13旋翼直径/m0．24飞行器机高/m0．165起落架的对角长度/m0．64旋翼中心到整机重心的距离/m0．32

四旋翼通过改变旋翼转速实现机动飞行,其飞行原理如图2～图5所示,通过实现不同旋翼的不同转速变化,进而实现飞行器的垂向、俯仰、偏航、滚转运动。

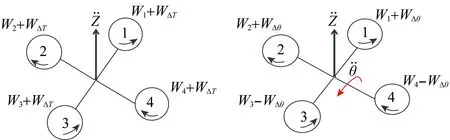
图2 四旋翼垂向运动 图3 四旋翼俯仰运动Fig.2 Vertical move of quad-rotor Fig.3 Pitch move of quad-rotor

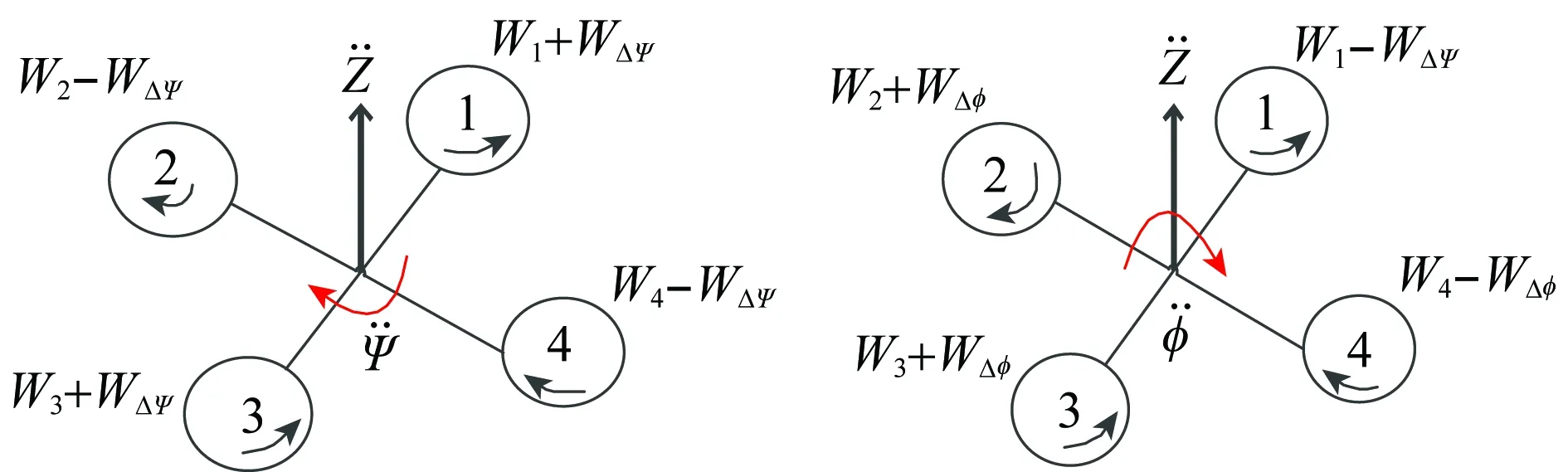
图4 四旋翼偏航运动 图5 四旋翼滚转运动Fig.4 Yaw move of quad-rotor Fig.5 Roll move of quad-rotor

1.2 考虑不确定性的四旋翼飞行器建模

考虑四旋翼飞行器模型存在的结构参数不确定性,定义如下符号:

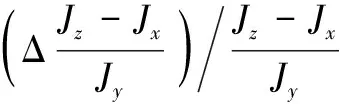
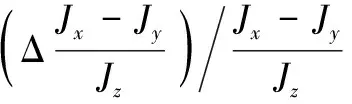
Δa4=ΔJx/Jx,Δa5=ΔJy/Jy

Δa6=ΔJz/Jz,Δa7=Δm/m

Δa12=Δjrz/jrz,Δa13=ΔCQ/CQ

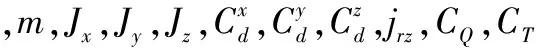
[12]可知,四旋翼飞行过程中所受扰动力主要形式为近地时变风,将扰动力Fdx,Fdy,Fdz引入参考文献[13]中飞行力学模型,则可构建考虑不确定性和外部扰动的四旋翼飞行器运动学与动力学方程为

(1)

2 四旋翼飞行器Lyapunov鲁棒动态逆控制器设计

2.1 基于时标分离原则的双回路模型建立

四旋翼飞行动力学模型为欠驱动模型,即通过四维度的旋翼转速变量控制六自由度运动。该特性使得各通道之间存在强耦合,给控制器设计带来了一定难度。因此采用“时标分离”方法[14],将四旋翼控制回路按对状态向量的响应速度不同进行划分,分为快回路和慢回路。其中,快回路为姿态跟踪回路;慢回路用来跟踪四旋翼的位置和速度。各回路使用虚拟控制量进行控制器设计。

多回路模型系统结构图如图6所示。

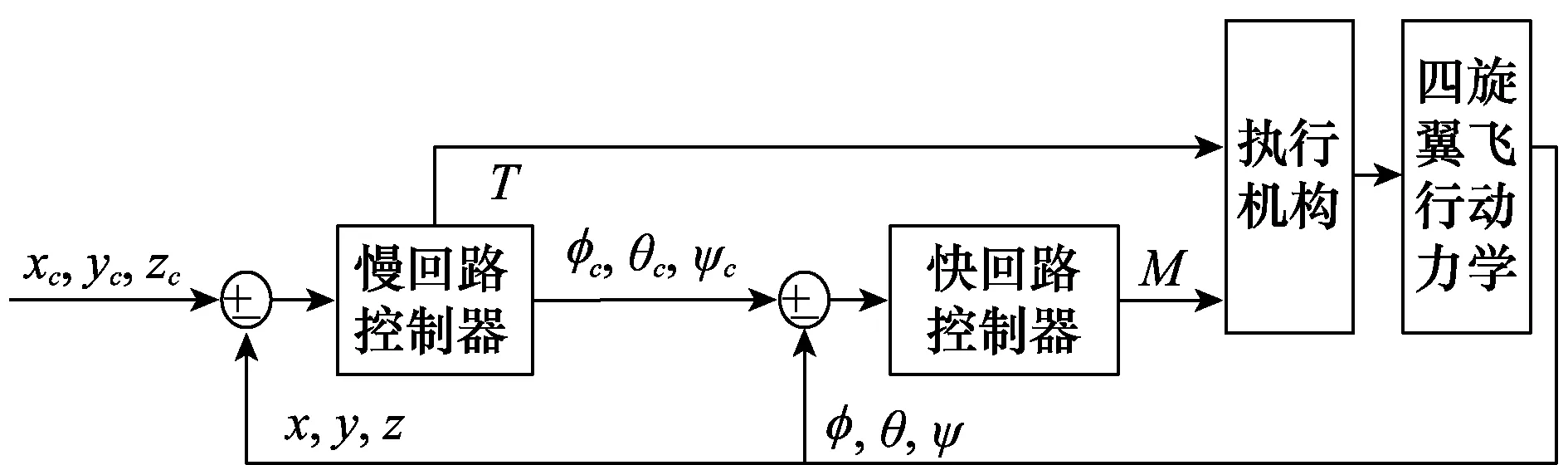
图6 双回路四旋翼飞行器控制系统结构图Fig.6 Structure of double-loop quad-rotor control system

(2)

下文将基于该双回路控制系统结构进行四旋翼飞行器的控制系统设计。

2.2 基于Lyapunov方法的控制律设计

基于式(1)和姿态小角度假设,对系统模型中非线性项进行线性化处理,同时消除各通道间的耦合项,则可将外环位置回路和内环姿态回路表示为

(3)

式中

用e1代表飞行器的指令跟踪误差:e1=x-xd,同时定义如下两个变量:

(4)

式中,α1,α2均为正常值控制增益。基于式(4)定义可知:

r(t)→0⟹e2(t)→0⟹e1(t)→0

由于内外环模型形式相同,下面仅以外环位置控制为例,进行控制律设计过程叙述。结合式(3)、式(4),可以得出系统跟踪误差模型:

(5)

考虑到系统模型存在结构误差,且外部干扰存在,系统的输入矩阵g包含不确定项,将g转化为

g=g0Δg

(6)

式中,g0∈Rn×n为名义模型的输入矩阵;Δg∈Rn×n为不确定矩阵,该矩阵为一个对角阵,反映了系统参数m,Jx,Jy,Jz的不确定性。

实际工程中结构模型不确定性矩阵Δg一般满足不等式:

1-ε≤‖Δg‖i∞≤1+ε

(7)

式中,ε∈(0,1)是一个已知的正值。

将式(6)代入式(5)可得

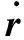
(8)

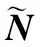
(9)

可以设定[16-17]:

(10)

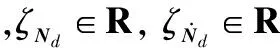
根据上述推导以及式(4),设计控制律:

(11)

将式(11)代入系统跟踪误差模型(5),可得闭环跟踪误差系统为

(12)

第2.3节将对该控制律的稳定性进行证明。

2.3 控制律全局渐进稳定性证明

定理1若式(11)中参数k1足够大,且β满足以下条件[18]:

(13)

其中,各参数定义与第2.2节中定义相同,α1>0.5,α2>0.5,β,α1,α2,k参数可调节系统的超调量、跟踪精度等,从而改善系统的控制性能,则控制律(11)能够满足系统的渐进稳定性:

‖e1(t)‖→0，t→∞

首先引入引理1。

(14)

式中

L(t)=rT(Nd(t)-Δgβsgn(e2))

(15)

若式(13)条件满足,则可以推出不等式

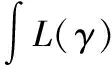
(16)

因此,由式(16)可以得出P(t)≥0。

接下来对定理1进行证明。

证明定义非负函数V(w,t):Ω×[0,∞)→R:

(17)

若式(13)中条件能够满足,则V(w,t)满足不等式

U1(w)≤V(w,t)≤U2(w)

(18)

式中,正定函数U1(w),U2(w)∈R具体形式为

U1‖w‖2,U2‖w‖2

(19)

基于以上定义,对式(17)关于时间t求导可得

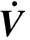
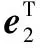
(20)

对式(20)进行整理消元,可得

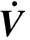
(21)

考虑式(7)与式(9),同时利用不等式

(22)

则式(21)满足不等式

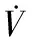
(1-ε)k1‖r‖2+ρ(‖z‖)‖z‖‖r‖

(23)

对式(23)右半部分进行转化,即

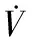
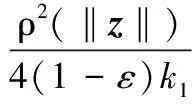
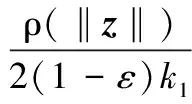
(24)

由于(1-ε)>0,k1>0,同时基于α1、α2的最小值推导出

‖z‖2

(25)

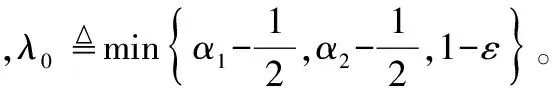
当k1足够大时,从式(25)可以推导出

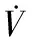
(26)

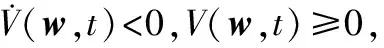
V(w,t)→0|t→0

(27)

根据式(16)可以得到

V(w,t)→0⟹e1→0,e2→0,r→0

(28)

至此,可以证明闭环误差跟踪系统是渐进稳定至0的。

证毕

3 基于Super-twisting算法的滑模干扰观测器设计

基于Lyapunov方法的鲁棒控制器在结构不确定性范围内的收敛性已经在第2节进行了理论证明。然而,由于四旋翼飞行器体积小,质量轻,在飞行中易受到外部扰动影响,且在前述线性化模型推导时忽略了飞行动力学中的非线性项和耦合项,因此必须对包括外部扰动在内的复合扰动进行观测并补偿,进而增强控制器的抗扰动性能,提高控制器的实际应用可行性。

3.1 基于Super-Twisting算法的滑模观测器设计

考虑四旋翼飞行器在飞行过程中易受到外部扰动影响,且主要以扰动力形式存在,对轨迹跟踪回路影响大,为了降低实际应用的复杂度,考虑仅对慢回路进行滑模干扰观测器设计,以补偿校正外部扰动力的影响。

将受扰动的四旋翼飞行动力学表述为

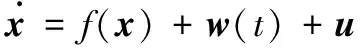
(29)

式中,u表示动态逆控制器产生的控制量;w(t)表示系统所受外部扰动;f(x)描述了参考模型的系统变化特性。

由式(29)可以推出

(30)

式中,ud为外部扰动设计补偿控制量,能使得w(t)+ud→0,即ud的相反数为外部扰动的滑模观测值。

基于Super-twisting算法,可以设计滑模控制律[19]为

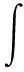
(31)

代入式(30)中可以得到

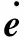
(32)

至此,基于滑模观测补偿的鲁棒动态逆四旋翼无人机控制器已经设计完成,结构框图如图7所示。

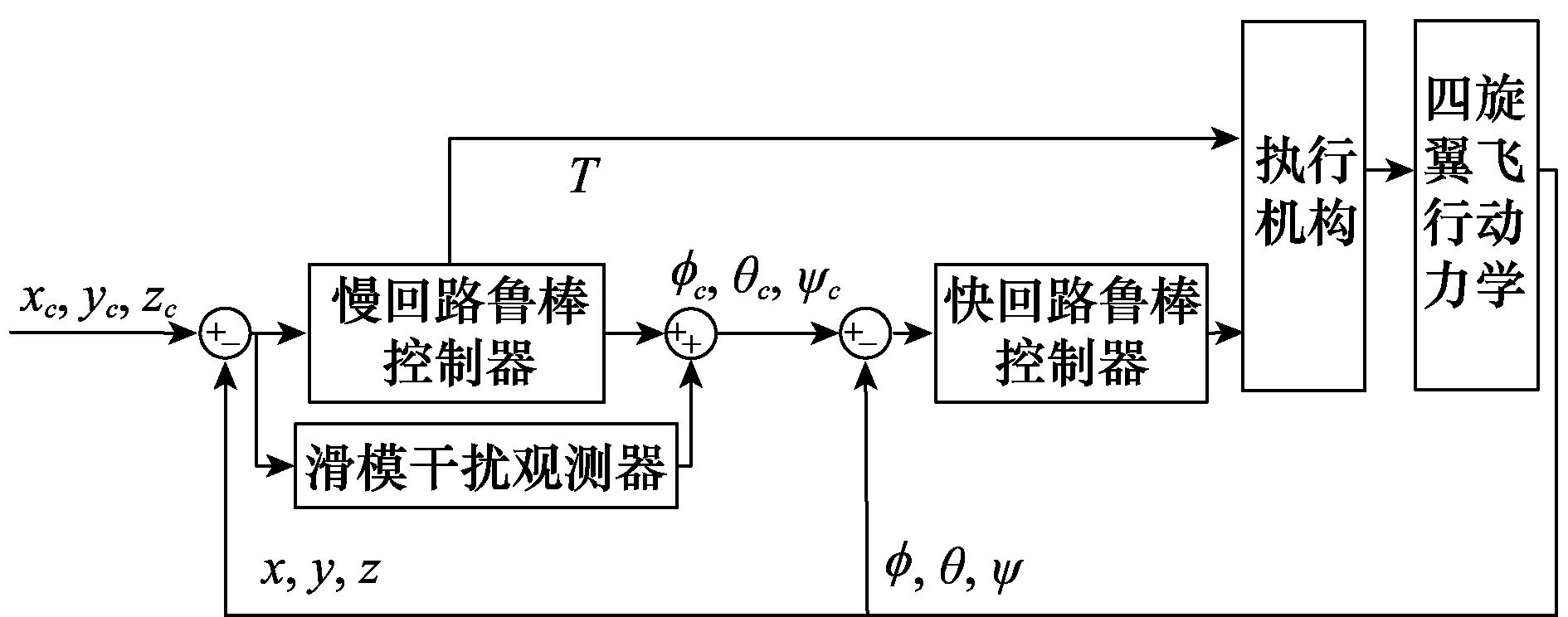
图7 基于滑模观测补偿的鲁棒动态逆控制系统结构图Fig.7 Structure of robust dynamic inversion control system based on sliding mode observation and compensation

3.2 滑模观测器收敛性证明

将式(32)转化为

(33)

假设外部干扰w(t)是可微的,且满足

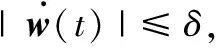
∀t≥0

(34)

式中,δ为一个正常数。

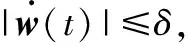
(35)

则系统(32)能够在有限时间内收敛到原点。

证明取对称正定矩阵

对ζ求导可得

(36)

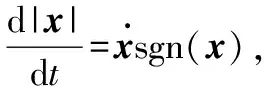
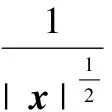
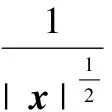
(37)

令Q=-(ATP+PA+δ2CTC+PBBTP),则

(38)

由式(36)可得

(39)

此时,当系统参数满足式(35)时,容易得出矩阵Q为正定矩阵,根据Lyapunov稳定性定义可知,系统能够收敛到原点。

证毕

4 仿真验证

4.1 仿真条件设置

基于文献[21]设计四旋翼飞行器参考轨迹,具体要求为:轨迹在机动结束点处飞行器的加速度和速度均为0,且到达目标点,其参考轨迹形式为

(40)

设计参考轨迹飞行30 s,其中机动飞行20 s,后10 s为悬停状态,全机动飞行参考轨迹为

(1)t≤10

(2) 20≥t>10

将四旋翼飞行器的结构不确定性设定为

‖Δa4‖<0.1, ‖Δa5‖<0.1, ‖Δa6‖<0.1

‖Δa7‖<0.1, ‖Δa8‖<0.2, ‖Δa9‖<0.2

‖Δa10‖<0.2, ‖Δa11‖<0.2, ‖Δa12‖<0.1

‖Δa13‖<0.2

考虑在仿真过程中施加时变外部风干扰为

其中,前10 s动态飞行过程中外部风扰动为正余弦叠加形式,10 s后额外引入幅值为1 N的常值风干扰。

通过调试,将位置回路和姿态回路鲁棒控制律参数分别设计为

姿态回路

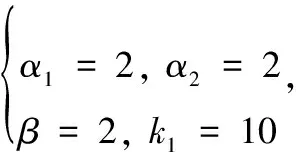
并将三通道的滑模观测器参数设计为

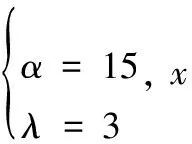
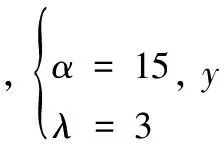
设定四旋翼飞行器初始状态为

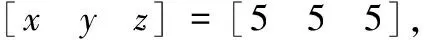
单位: m

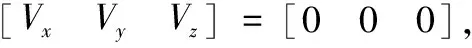
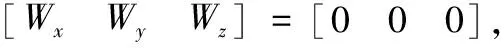
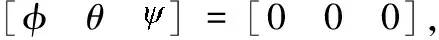
4.2 仿真结果与分析

首先在仿真中仅考虑四旋翼飞行器的结构参数不确定性,不引入外部风干扰,同时不引入Super-twisting干扰观测补偿器,则仿真结果如图8所示。

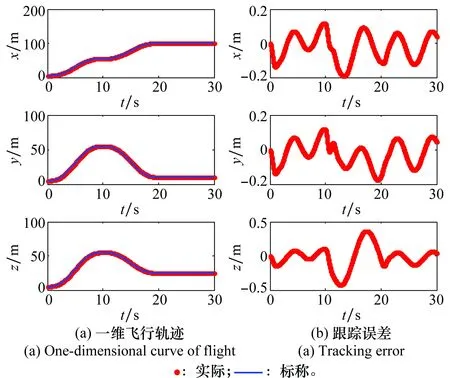
图8 考虑结构参数不确定性的一维飞行轨迹及误差图Fig.8 One dimensional curve of flight and tracking error with the existence of structural parameter uncertainty

图8(a)为飞行轨迹图,图8(b)为跟踪误差图。分析图像可得,在较大结构参数误差情况下,飞行全程三方向跟踪误差小于0.1 m,且悬停状态下稳态误差小于0.01 m,验证了内外环鲁棒控制器具有较强的鲁棒性。

考虑在仿真中引入如第4.1节所示的风干扰模型,其他仿真条件不变,则全程滑模干扰观测器观测结果如图9所示。

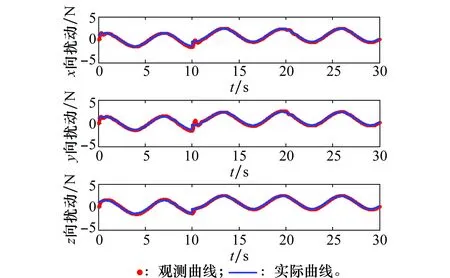
图9 外部扰动观测曲线Fig.9 Curve of observed external disturbance

从以上仿真曲线及仿真数据可以得出,由滑模观测器观测的外部扰动与实际扰动之间最大误差小于0.2 N,且20 s飞行时间内误差平均值小于0.1 N,表明滑模观测器能够实现对扰动较为精确的观测。虽然曲线中存在振颤以及放大扰动等现象,这是由于内环控制器的控制误差所致,即由于四旋翼飞行器姿态角无法完全跟踪姿态角指令所带来的附加扰动引起的。

为表述简便性,将引入滑模干扰补偿观测的鲁棒动态逆控制器描述为扩展鲁棒动态逆(extended robust dynamic inversion, ERDI)控制器,考虑结构参数不确定性和外部干扰仿真条件下对比鲁棒动态逆(robust dynamic inversion, RDI)控制器和ERDI控制器的控制效果,同时采用文献[22]中PID控制方法进行仿真,得到如图10所示的飞行轨迹。

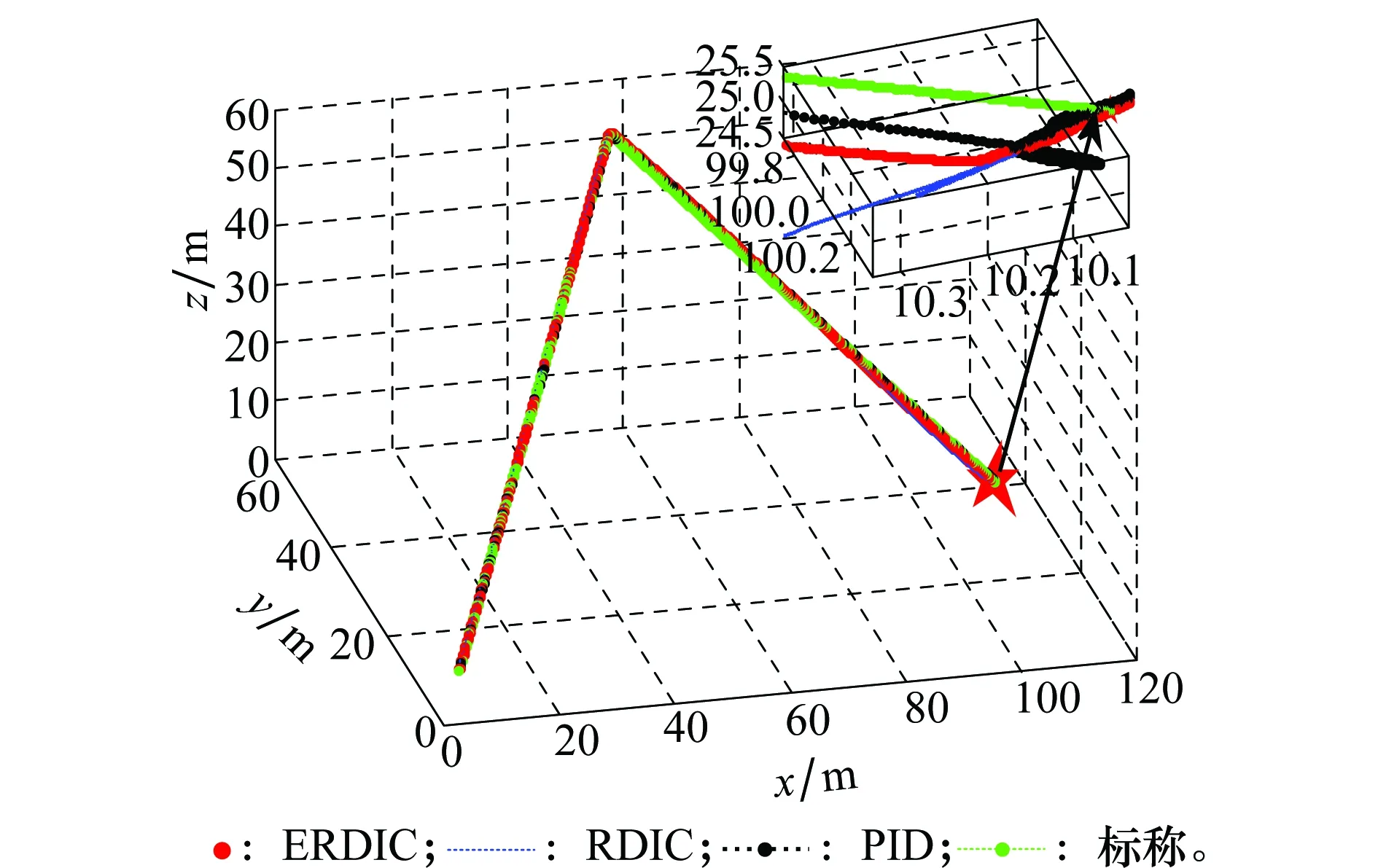
图10 不同控制方法作用下的飞行轨迹图Fig.10 Flight curve of quad-rotors under control of different algorithm

其中,“☆”即为30 s后四旋翼飞行器悬停点,图中放大的区域即为悬停点附近区域。

飞行轨迹跟踪误差曲线如图11所示。

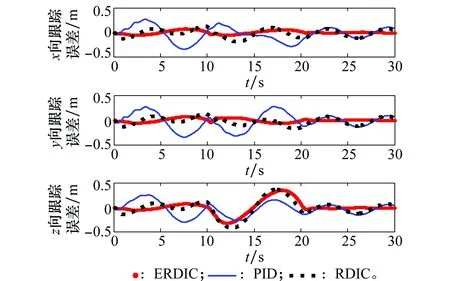
图11 不同控制方法作用下的跟踪误差曲线Fig.11 Curve of tracking error under control of different algorithm

不同控制方法下飞行全程跟踪误差均方根如表2所示。

表2 不同控制器作用下跟踪误差均方根

分析图 10、图 11、表 2可得,ERDI控制精度和抗干扰能力明显强于RDI控制器和PID控制器,验证了引入滑模观测补偿控制器的必要性以及ERDI控制器的强鲁棒性和抗扰性。

ERDI控制器作用下飞行全程四旋翼转速变化曲线如图12所示。

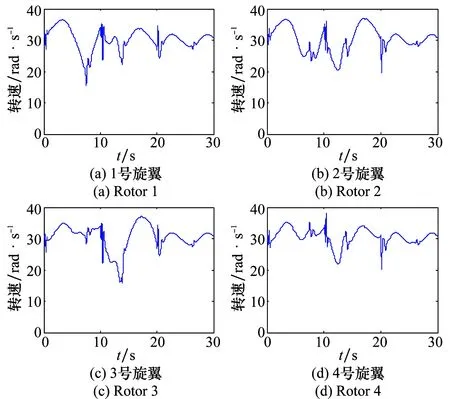
图12 旋翼转速变化曲线Fig.12 Curve of rotation speed of four rotors

分析图12可以看出,飞行全程旋翼转速变化较为平缓,且变化范围在15～38 rad/s,需要说明的是,曲线中10 s时旋翼转速出现短暂抖动,这是由突然施加的常值风干扰引起的,抖动持续时间小于1 s,进一步验证了ERDI控制器的抗扰性和实用性。

5 结 论

本文对四旋翼飞行器进行飞行原理分析和包含不确定性的飞行动力学模型建立,基于“时标分离”原理对模型进行了双回路分层,解决了飞行器欠驱动、强耦合等问题。在此基础上,考虑四旋翼模型的结构不确定性,基于Lyapunov原则设计了鲁棒控制律并给出全局收敛性证明。进一步,为应对飞行过程中的强外部扰动,利用Super-twisting算法设计了滑模干扰观测器,并基于干扰观测补偿设计了综合鲁棒动态逆控制器。通过仿真验证了本文所设计的基于滑模观测补偿的鲁棒动态逆控制器的强鲁棒性和强抗扰性。

参考文献：

[1] CAI G, WANG B, CHEN B M, et al. Design and implementation of a flight control system for an unmanned rotorcraft using rpt control approach[J].Asian Journal of Control,2013,15(1): 95-119.

[2] SALIH A L, MOGHAVYEMI M, MOHAMED H A, et al. Modeling and PID controller design for a quadrotor unmanned air vehicle[C]∥Proc.of the IEEE International Conference on Automation Quality and Testing Robotics,2010: 1-5.

[3] 高青,袁亮,吴金强.基于新型LQR的四旋翼无人机姿态控制[J].制造业自动化,2014,36(10): 13-16.

GAO Q, YUAN L, WU J Q. Attitude control of a quadrotor UAV based on new LQR[J].Manufacturing Automation, 2014, 36(10): 13-16.

[4] KHATOON S, GUPTA D, DAS L K. PID & LQR control for a quad-rotor. modeling and simulation[C]∥Proc.of the IEEE International Conference on Advances in Computing, Communications and Informatics, 2014: 796-802.

[5] LIN F J, FUNG R F, LIN H H, et al. A supervisory fuzzy neural network controller for slider-crank mechanism[C]∥Proc.of the IEEE International Conference on Control Applications, 1999: 1710-1715.

[6] EMAM M,FAKHARIAN A.Attitude tracking of quadrotor UAV via mixed H2/H∞ controller: an LMI based approach[C]∥Proc.of the 24th Mediterranean Conference on Control and Automation, 2016: 390-395.

[7] 王冬来,吕强,刘峰,等.基于L1自适应方法的四旋翼飞行器纵向控制[J].弹箭与制导学报,2011,31(6): 37-40.

WANG D L, LÜ Q, LIU F, et al. Quadrotor longitudinal controller based onL1adaptive control method[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(6): 37-40.

[8] KAYACAN E, MASLIM R. Type-2 fuzzy logic trajectory tracking control of quadrotor VTOL aircraft with elliptic membership functions[J]. IEEE/ASME Trans.on Mechatronics, 2017, 22(1): 339-348.

[9] RAHARJA N M, ISWANTO, WAHYUNGGO O, et al. Altitude control for quadrotor with mamdani fuzzy model[C]∥Proc.of the International Conference on Science in Information Technology, 2015: 309-314.

[10] SAFAEE B, MASHHADI S K M. Fuzzy membership functions optimization of fuzzy controllers for a quad rotor using particle swarm optimization and genetic algorithm[C]∥Proc.of the International Conference on Control, Instrumentation and Automation, 2006: 256-261.

[11] 李劲松,杨炼,王乐天.小型四旋翼无人直升机自适应优化控制[J].上海交通大学学报, 2015, 49(2): 202-208.

LI J S, YANG L, WANG L T. Control of small scale quad-rotor helicopter using adaptive control-optimization[J]. Journal of Shanghai Jiaotong University,2015,49(2): 202-208.

[12] ZHAO D J, YANG D G. Model-free control of quad-rotor vehicle via finite-time convergent extended state observer[J].International Journal of Control Automation & Systems,2016,14(1): 242-254.

[13] 黄依新.四旋翼飞行器姿态控制方法研究[D].成都: 西南交通大学,2014.

HUANG Y X. Research on attitude control for quad-rotor[D]. Chengdu: Southeast Jiaotong University, 2014.

[14] 王飞. 高超声速飞行器QFT/μ鲁棒动态逆控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.

WANG F.QFT/μ robust dynamic inversion control of hypersonic vehicle[D].Harbin: Harbin Engineering University,2013.

[15] LIN Q, CAI Z, YANG J, et al. Trajectory tracking control for hovering and acceleration maneuver of quad tilt rotor UAV[C]∥Proc.of the IEEE Control Conference, 2014: 2052-2057.

[16] BHASIN S, KAMALAPURKAR R, JOHNSON M, et al. A novel actor-critic-identifier architecture for approximate optimal control of uncertain nonlinear systems[J]. Automatica, 2013, 49(1): 82-92.

[17] BIDIKLI B, TATLICIOGLU E, BAYRAK A, et al. A new robust ‘integral of sign of error’ feedback controller with adaptive compensation gain[C]∥Proc.of the IEEE Conference on Decision and Control, 2013: 3782-3787.

[18] TON C T, MACKUNIS W. Robust attitude tracking control of a quadrotor helicopter in the presence of uncertainty[C]∥Proc.of the IEEE Conference on Decision and Control, 2012: 937-942.

[19] LEVANT A. Robust exact differentiation via sliding mode technique[J]. Automatica, 1998, 34(3): 379-384.

[20] MORENO J, OSORIO M. Strict Lyapunov functions for the super-twisting algorithm[J]. IEEE Trans.on Automatic Control, 2012, 57(4): 1035-1040.

[21] ABHIJIT D, FRANK L L. Sliding mode approach to control quadrotor using dynamic inversion[M]. Rijeka: InTech Press, 2011: 3-22.

[22] JUNIOR J C V, PAULA J C D, LEANDRO G V, et al. Stability control of a quad-rotor using a PID controller[J]. Brazilian Journal of Instrumentation & Control, 2013, 1(1): 15.