铣刨机输出功率模型的研究
管付银,孙瑞峰
铣刨机是一种路面铣刨机械,即道路养护机械。铣刨机工作时,主要是把损坏的路面铣刨起来,从而铺上新的面层。铣削功率要受诸多因素的影响,既与铣刨机自身的参数有关,又与作业对象有关系,还与铣刨机的作业状态有关。铣刨机按铣削方式分顺铣和逆铣,如图1所示。

图1 铣刨机工作原理图
铣刨机在铣削沥青路面时,铣刨速度无法保证完全不变,铣刨机输出功率随着速度的变化发生变化,铣刨机输出功率曲线呈间歇性分布。机械传动很难保证铣刨转子速度进行连续调节[1]。但是铣刨机的行驶速度很容易进行调节。并且铣刨机铣刨作业所消耗的功率与铣刨机的行驶速度的平方有一定的函数关系[2]。目前国内尚缺乏有关铣刨机功率预测方面的理论研究,开展铣刨机功率预测的研究能为铣刨机功率高效率的应用提供理论依据,例如铣削不同材料,不同深度的路面就需要不同的功率,目前铣刨机改变铣削过程的功率主要是改变铣刨机油门的开度,这就需要高经验的操作人员,增加了成本。
为此,本文对铣刨机功率模型进行了研究,包括铣刨机基本功率方程模型和铣刨机功率曲线模型两个方面。
1 铣刨机基本功率方程模型
如图1所示,铣刨机铣削与其他切削加工一样,当铣刨鼓齿数为Z时,其单位体积的路面材料所消耗的切削功应为[3]:

根据对铣刨机输出功率影响因素的理论分析,通过公式推导以及整合,为了区分各种变量,假设fZ为铣刨转子系统铣削路面每齿的进给量,vT为铣刨鼓刀尖的铣削速度,Pm为消耗功率。

将以上公式(1)、(2)(3)中并且整理公式得到:


公式中的含义为:
铣刨机额定条件下的功率为Pm;铣刨机的额定功率为P1;铣刨鼓上刀头的个数为Z;铣削厚度为ae;铣刨鼓的半径为R;铣刨鼓的角速度为ω¯;单刀头的铣削宽度为ap;铣刀前刀面摩擦角为β;铣刨刀具实际切削前角为γ0;被铣刨材料的劈裂破坏强度为τs;π为常数;铣刨机行驶速度为v.
铣刨机输出功率的主要影响因素有铣削厚度、铣刨机速度及铣刨鼓的半径。
为了得到功率曲线,在铣刨鼓上安装速度传感器和单刀铣削三向力传感器,利用DEWESoft数据采集系统测得六组速度与力的关系数据,再利用(5)公式的变换成六组离散速度与功率的数据点,如图2黑色圆点,根据这些黑点再利用作图工具绘制铣刨机的输出功率曲线,如图2、图3所示。

图2 输出功率曲线图
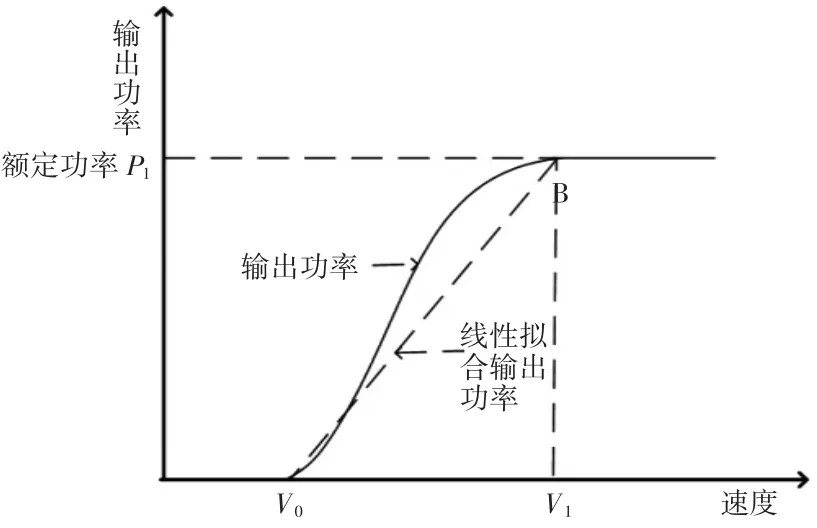
图3 输出功率曲线与线性模型拟合的假定的功率曲
由图2,铣刨机的输出功率曲线可用分段函数表示为:

其中,V0表示铣刨机输出功率的初始速度,V1为铣刨机输出额定功率的额定速度。
2 铣刨机的功率曲线模型
由于铣刨机实际功率曲线模型计算比较复杂,要想达到高效率的应用发动机的功率和减少发动机的功率损失以及获得高质量的路面,操作铣刨机需要高经验的工作人员,增加了成本,而利用假定的功率曲线模型可以不需要上面的条件就可以达到目的,所以在一定条件下,假定的功率曲线模型可以代替铣刨机实际功率曲线模型。
利用数值分析原理中离散点可以通过曲线拟合的方法可以近似表示,故铣刨机假定的功率曲线模型可以利用功率曲线来表示,主要是指假定的功率曲线模型。
2.1 假定的功率曲线模型
假定的功率曲线模型主要包括线性模型、二次方模型、三次模型等等。
2.1.1 线性模型
铣刨机的输出功率采用线性模型,其中输出功率模型为:

利用数学方法进行确定线性方程的系数。

通过确定常数a,b,把常数a,b代入线性模型,得到线性模型公式。利用绘图软件,在图1的基础之上绘制线性曲线(虚线表示),如图3所示。通过图3实线与虚线相比较,即铣刨机的输出功率曲线与线性模型拟合的假定的功率曲线模型进行比较。从图中可以看出铣刨机的输出功率曲线与线性模型拟合的假定的功率曲线模型有一定的偏差,但是在一定的条件下可以近似代替。但是无法准确地表达出真实铣刨机功率情况,由于铣刨机实际功率曲线模型计算比较复杂,在一定条件下,假定的功率曲线模型可以代替铣刨机实际功率曲线模型。
2.2.2 二次方模型
如铣刨机的输出功率采用二次方模型,其输出功率模型主要有两种,第一种模型为:

利用数学方法进行确定一元二次方程的系数。式中,

第二种模型为:

2.2.3 误差估计
通过铣刨机试验台速度传感器在V0<V<V1区间内任测多点,假定的功率通过公式(8)计算。
v0=4时,实际功率pm0=50 kW,假定的功率pm00=45 kW
v1=5.3时,实际功率pm1=64.6 kW,假定的功率pm11=68 kW
v2=5.6时,实际功率pm2=67.6 kW,假定的功率pm22=73 kW
v3=68时,实际功率pm3=70.6 kW,假定的功pm33=81 kW
v4=9.65时,实际功率pm4=80 kW,假定的功率pm44=88 kW
两次测得的数据误差为:

通 过 计 算 得 到 δ0=0.1,δ1=0.05,δ2=0.08,δ3=0.14,δ4=0.1均小于0.2(标准值)可以认为误差合理。
由于误差较小所以在一定的条件下可以认为铣刨机假定的功率曲线模型是一种简化模型,具有一定的代表性,但是无法准确的表达出真实铣刨机功率情况。由于铣刨机实际功率曲线模型计算比较复杂,在一定条件下,假定的功率曲线模型可以代替铣刨机实际功率曲线模型。
[1]陆青平.铣刨机自功率控制系统的研究[D].西安:长安大学,2002.
[2]马鹏宇,胡永彪.轮式铣刨机自功率及数字调速系统研究[J].筑路机械与施工械化,2004,21(11):26-28.
[3]赵 敏.沥青路面铣刨机作业阻力及牵引性能的研究[D].西安:长安大学,2003.

