累积损伤模型下Lomax分布产品序进-恒定加速试验分析★

和阳，王蓉华，徐晓岭

（1.上海师范大学数理学院 上海 200234；

2.上海对外经贸大学统计与信息学院 上海 201620）

0 引言

Abd Ellah，A H在文献 [1]中将Lomax分布称为第二型的Pareto分布，该分布的失效函数具有单调递增和单调递减的性质，在分析医学、生物科学和工程科学等方面有重要的贡献。关于该分布的统计推断理论引起了很多统计学者的兴趣，并在此之前做了大量的相关研究工作。例如：文献 [2]研究了损伤失效率下两参数Lomax分布在步进应力加速寿试验下参数的极大似然估计和近似区间估计；文献 [3]研究了在累积损伤模型下两参数Lomax分布产品在序进应力加速寿命试验下参数的极大似然估计和近似区间估计；文献 [4]在熵损失下，已知两参数Lomax分布中的尺度参数时，得到了形状参数的Bayes估计；文献 [5]在研究了在累积损伤模型下，Lomax分布在简单步进应力加速寿命试验下参数的极大似然估计，同时还讨论了参数的渐进方差-协方差矩阵，给出了基于渐进正态性的近似区间估计，通过似然比的方法得到了参数的假设检验；文献 [6]讨论了在Linex损失函数下，Lomax分布中形状参数的E-Bayes点估计，运用Monte Carlo方法模拟数据，比较了不同的估计值；文献 [7]讨论了Lomax分布的参数的区间估计和对应的假设检验；文献 [8]讨论了服从Lomax分布的产品的次序失效时间的性质和渐进分布；文献 [9]讨论了在Linex损失函数下，Lomax分布中已知尺度参数的前提条件下，形状参数的Bayes估计和多层Bayes估计。本文讨论了累积损伤模型下，Lomax分布在序进—恒定应力 （V1=0）加速寿命试验的失效模式以及参数的极大似然估计和近似区间估计。

设某产品的寿命T服从Lomax分布，其分布函数与密度函数分别为：

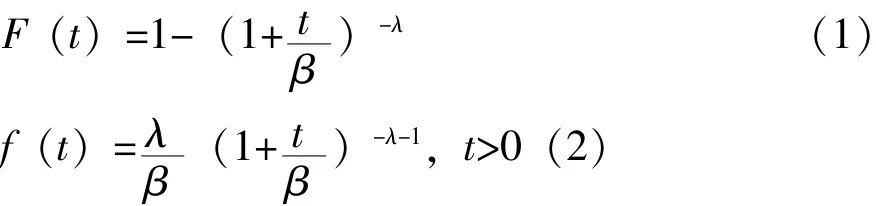
式（1）-（2）中：β——尺度参数；

λ——形状参数。

1 逆幂律模型、Nelson假定和渐进正态性

逆幂律模型是指在加速寿命试验过程中，以电压作为加速应力时，根据物理原理和试验的经验总结，发现有些产品 （例如：绝缘材料、电容器、微型电机和某些电子器件等）的刻度参数β（单位：h）和电压 （单位：V）之间有如下关系 （称为逆幂律关系）：

式（3）中：d、c——常数，且d＞0，c＞0。

当产品是电子元器件时，物理实验表明c仅与元器件的类型有关，而与其规格无关。

对上式两边同时取对数后可得，β满足对数线性关系：

其中，a=-lnd，b=-c，φ（V）=lnV是应力V的函数。

关于步进应力或序进应力加速寿命试验的统计分析大多是建立在Nelson假定 （简称CE模型）基础上的。

Nelson假定[11]：产品的残余寿命仅依赖于当时已积累失效的部分和当时的应力水平， 而与积累方式无关。

Nelson假定其实就是一种 “时间折算”，即如果持续在一个恒定应力下，未失效的产品会根据该应力下的分布函数来失效， 但是要从以前累积失效的部分开始算起。

设在恒定应力Vi，i=1，2下产品的寿命Ti服从Lomax分布，其分布函数为：

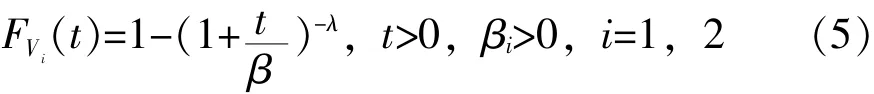
由Nelson假定知：

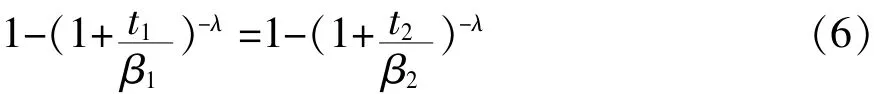
即

上式可以解释为：产品在恒定加速应力V2下工作t2时间，相当于在恒定加速应力V1下工作t1=时间。

定理[12]：假设Θ为开区间，概率密度函数f（x； θ）， θ∈Θ满足以下条件。

1） 在参数真值 θ0的领域内，对所有的t都存在；

2）在参数真值θ0的领域内H （t）， 且 EH （t） ＜∞；

3）在参数真值θ0处，

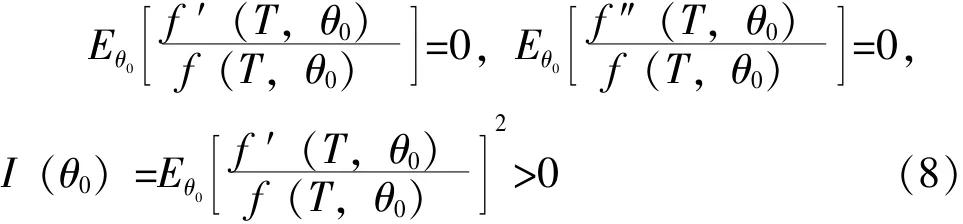
其中，撇号表示对θ的微分，记θˆn为n→∞时似然方程的相合解，则：

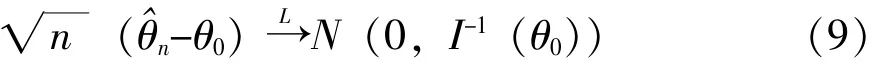
2 Lomax分布的产品在序进-恒定应力加速寿命试验下的失效模式

考虑序进-恒定应力加速寿命试验，在这个试验中，n个产品在序进应力V （t）=Kt+V1，V1≥0下做加速寿命试验，同时考虑到应力过大有可能会改变产品的失效机理，因此产品在序进应力V（t）=Kt+V1下试验持续到时间τ时 （其间共有r个产品失效），将试验应力稳定在Kτ+V1继续试验，直至产品全部失效，试验终止。

此时应力水平有如下表示：

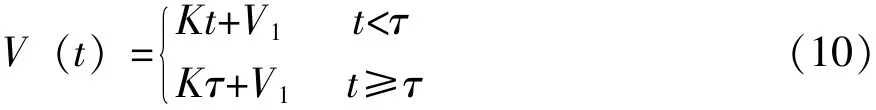
首先，考虑产品在序进应力V（t）=Kt+V1，V1≥0下的加速寿命试验，试验持续到时间τ时共有r个产品失效，假定在应力V1下产品的寿命分布服从Lomax分布，而尺度参数β1满足逆幂律模型：

由文献 [13]可知：在应力V（t）=Kt+V1，V1≥0下工作了t时间，相当于在恒定应力V1下工作的时间为：

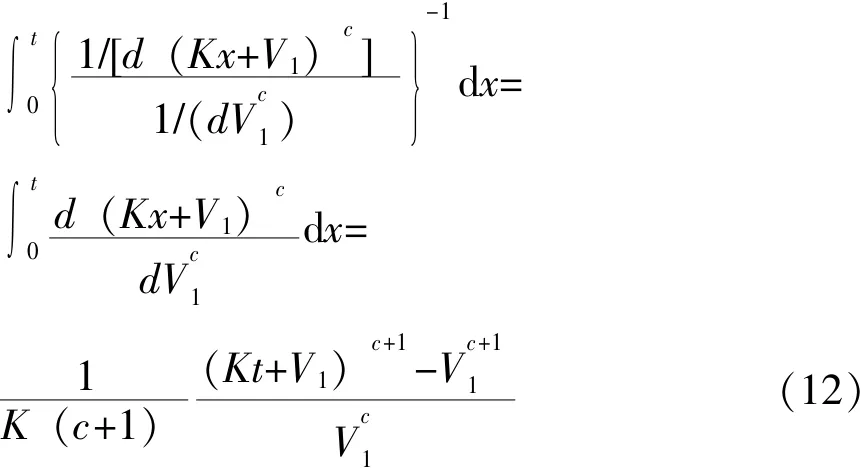
则由Nelson假定知，产品在在序进应力V（t）=Kt+V1，V1≥0下的寿命分布为：

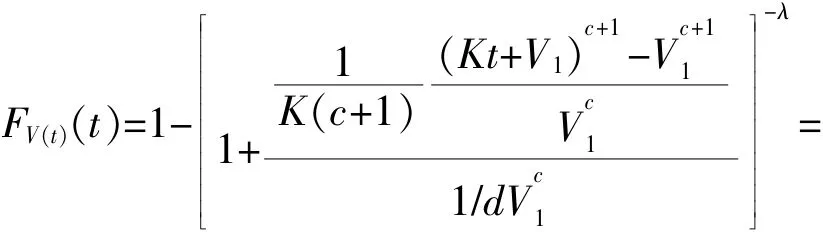
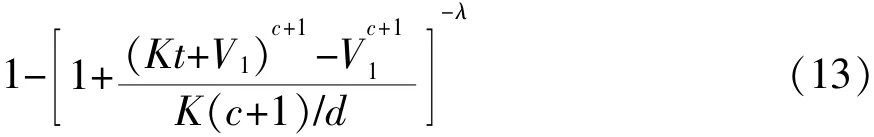
特别地，当V1=0时，即产品在序进应力V（t）=Kt下的寿命分布为：

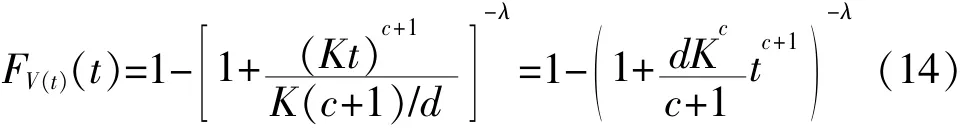
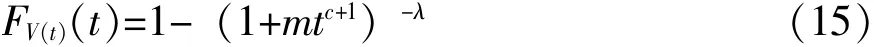
其次，产品在序进应力V（t）=Kt+V1下试验持续到时间τ后，为了防止改变产品的失效机理，未失效的产品在恒定应力Kτ+V1下继续试验，直到剩余的产品全部失效，试验终止。

在恒定应力Kτ+V1下产品工作的时间记为t-τ（都是从时刻0算起），其相当于在应力V1下工作的时间为

因此，在时刻τ之前未失效的产品，其工作至t时刻的工作时间相当于在恒定应力V1下的工作时间为：

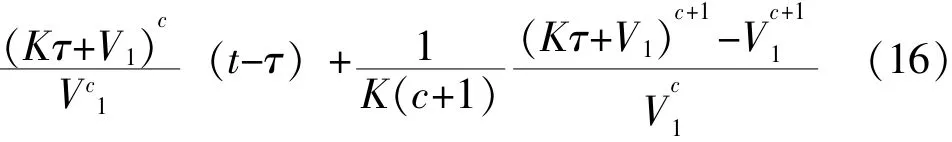
此时，在逆幂律模型下，产品的寿命分布为：FV（t）（t）=

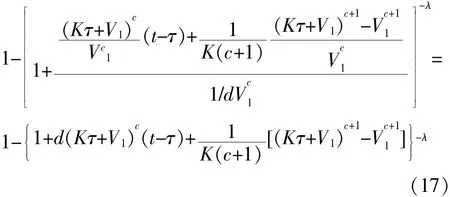
特别地，当V1=0时，产品的寿命分布为：

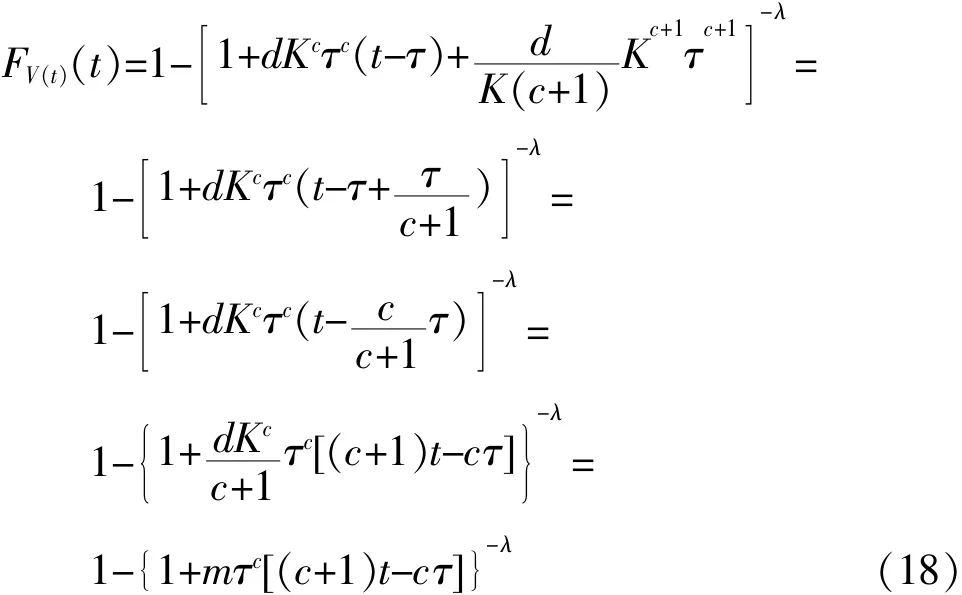
3 Lomax分布的产品在序进-恒定应力 （V1=0）加速寿命试验下的可靠性统计分析

考虑序进-恒定应力加速寿命试验，在这个试验中，将n个产品在序进应力V （t）=Kt下做加速寿命试验，当试验持续到时间τ时 （其间共有r个产品失效， 其次序失效时间记为： t（1）， t（2）， …，t（r）），为了防止改变产品的失效机理，此后将试验应力稳定在Kτ，继续对未失效的产品做加速寿命试验，直至产品全部失效，试验终止，其次序失效时间记为： t（r+1）， t（r+2）， …， t（n））。

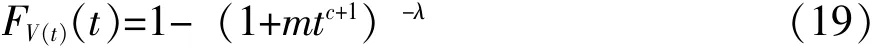
密度函数为：

当t≥τ时，产品服从如下的分布函数：

密度函数为：

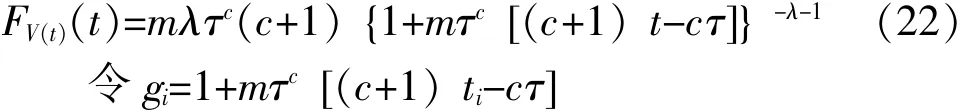
则似然函数为：

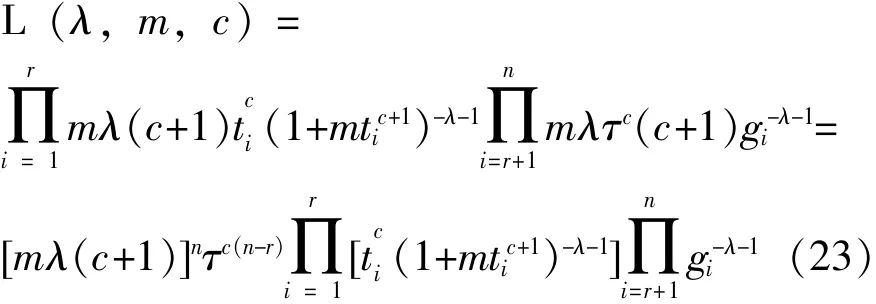
对数似然函数为：

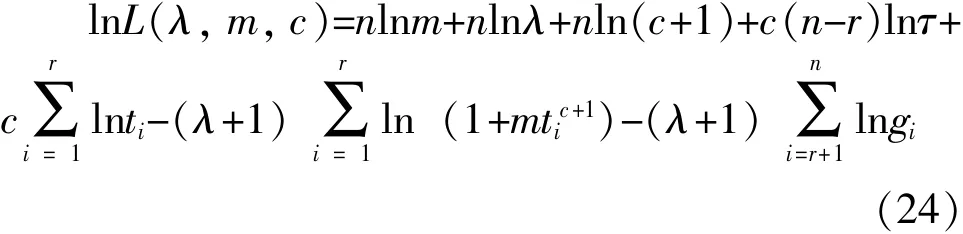
分别求lnL（λ，m，c）对λ、m、c的偏导数：

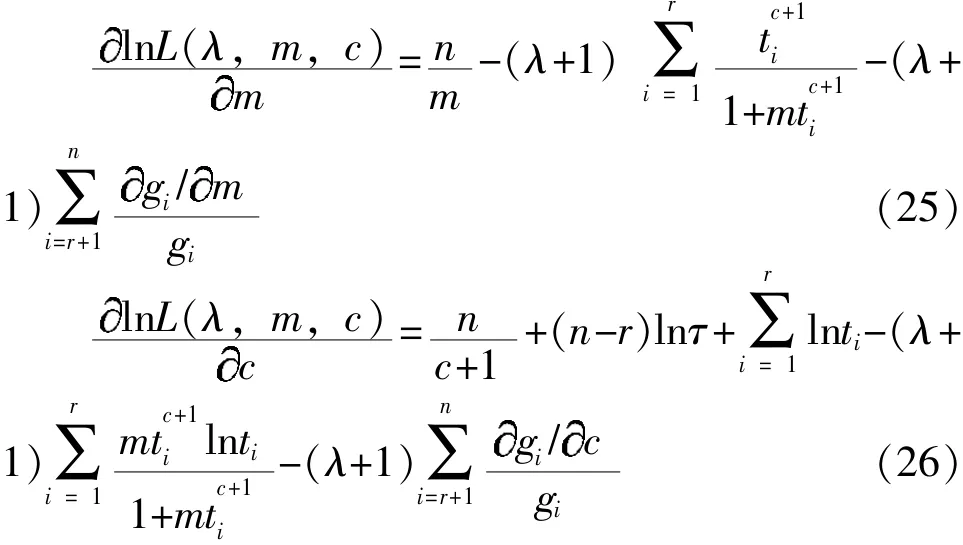
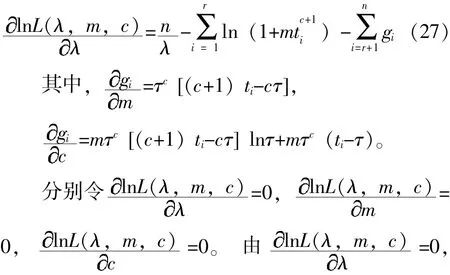
分别求lnL对λ、m、c的二阶偏导数：

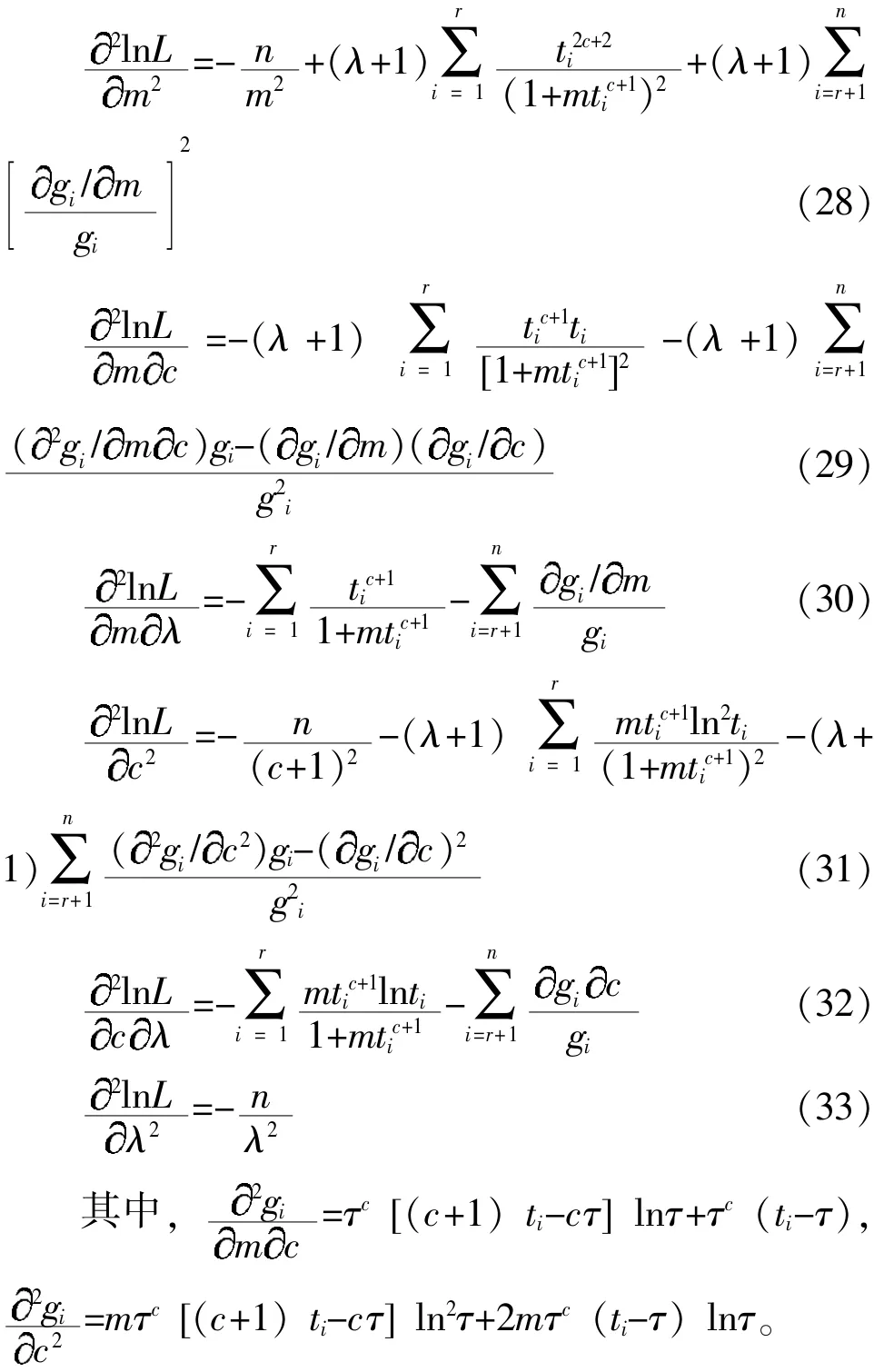
由此可得fisher信息阵为：

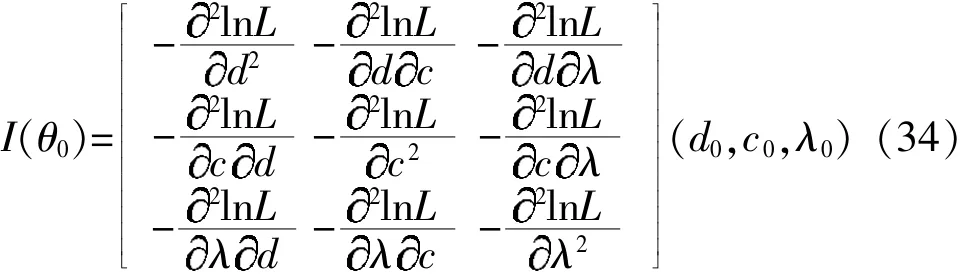
取置信度为1-α，则d的置信区间为： （d0-同理，c的置信区间为：λ 的置信区间为： （λ0-

4 Monte Carlo算例

0.175 2 0.180 3 0.189 7 0.193 9 0.237 60.282 4 0.282 7 0.300 9 0.307 5 0.350 80.406 3 0.421 9 0.434 9 0.497 1

在恒定应力Kτ下的失效时间为： 0.537 0 0.556 7 0.658 3 0.886 7 0.911 4 0.930 7

由上面的结论，得到fisher信息阵为：

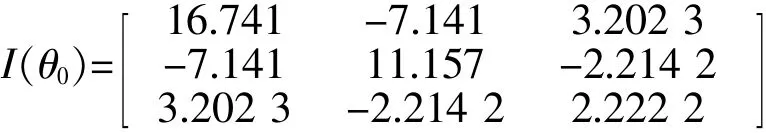
取置信区间为95%，从而得到参数m的区间估计为： （0.391 7，1.608 3），参数c的区间估计为： （0.292，1.708），参数λ的区间估计为：（1.410 7， 4.589 3）。

5 结束语

为了提高试验效率，减少成本，人们需要尽可能地利用有限的资源得到产品的寿命信息。本文讨论了在累积损伤模型下，服从Lomax分布的产品在序进-恒定应力加速寿命试验下的参数极大似然估计和基于渐进正态性的近似区间估计，并用Monte-Carlo法模拟数据，计算了参数的极大似然估计和近似区间估计。得到如下结论：

1）序进-恒定应力加速寿命试验确实可以提高试验效率，缩短试验时间；

2）在序进-恒定应力加速寿命试验下得到的参数估计仍然能够反映真实的产品信息；

3）基于渐进正态性的近似区间估计能够很好的包含极大似然估计。

[1]ABD Ellah，A H.Bayesian one sample prediction bounds for Lomax distribution[J].Indian J Pure and Applied Mathematics， 2003， 34 （1）： 101-109.

[2]肖小英，任海平.熵损失函数下两参数Lomax分布形状参数的Bayes估计 [J].数学的实践与认识，2010，40（5）： 227-230.

[3]周明元.对称熵损失函数下两参数Lomax分布形状参数的Bayes估计 [J].统计与决策，2010（12）：8-10.

[4]王琪，任海平.NA样本下两参数分布Lomax形成参数的经验Bayes检验 [J].统计与决策，2010（12）：161-162.

[5]姚惠，谢林.不同损失下Lomax分布形状参数的Bayes估计 [J].数学杂志，2011（6）：31-37.

[6]姚惠.Linex损失下Lomax分布形状参数的Bayes估计[J].统计与决策，2011（16）：173-175.

[7]姚惠，吴现荣.Linex损失下Lomax分布形状参数的几种Bayes估计 [J].黔南民族师范学院学报，2012，31（6）： 113-116.

[8]龙兵.两参数Lomax分布次序统计量的性质和渐进分布[J].兰州交通大学学报，2013，32（4）：164-167.

[9]龙兵.两参数Lomax分布中参数的区间估计和假设检验[J].江西师范大学学报，2014，38（2）：176-179.

[10]AMAL S Hassan，AMANI S Al-Ghamdi.Optimum ztep stress accelerated life testing for Lomax distribution[J].Journal of Applied Sciences Research， 2009， 5 （12）：2153-2164.

[11]NELSON W.Accelerated life testing step-stress models and data analysis[J].IEEE Transactions on Reliability，1980， 29 （2）： 103-108.

[12]茆诗松，王静龙，濮晓龙.高等数理统计 （第二版）[M].北京：高等教育出版社，2006：120-121.

[13]NELSON W.Accelerated testing statistical models，test plans， and data analysis[M].New York： John Wiley&Sons， Inc.， 2004： 507-509.