键合丝随机振动应力极限仿真分析

朱朝轩，罗俊，杨少华

（1.中国电子科技集团公司第二十四研究所，重庆 40060；2.工业和信息化部电子第五研究所，广东 广州 510610）

0 引言

随着半导体集成电路朝着微型化、低功耗、智能化和高可靠性的方向发展，封装技术也在不断地革新。在半导体集成电路的封装工艺中，内部器件的互连是整个工艺的关键。目前，引线键合因具有工艺简单、成本低廉和适用多种封装形式等优点而在连接方式中占主导地位，并广泛地应用于集成电路封装领域。因此，键合的质量和可靠性也直接决定了集成电路封装的质量与可靠性。据统计，在半导体器件的失效模式分布中，引线键合失效占了器件总失效的1/4～1/3[1]。但目前设计人员在选择键合丝时，往往只考虑最大额定电流和简单的力学性能，而且在制定器件随机振动试验方案时，没有相关可靠的键合丝应力信息作为参考。因此，本文基于仿真分析，获得了不同材料、丝径、键合形式和跨度的键合丝随机振动极限应力及其对应的功率谱密度 （PSD：Power Spectral Density），为键合设计和选型提供了一定的参考。

1 键合形式及其特点

引线键合工艺分为热压键合、超声键合和热超声键合3种，主要影响焊点与焊盘结合面的质量，不会改变键合丝自身的结构和力学性能，故不考虑键合工艺对键合丝极限应力的影响[2]。而引线键合的形式有如图1-2所示的球键合与楔键合两种，键合形式和劈刀是键合丝结构和形貌的主要影响因素，其主要特点如表1所示[3-5]。

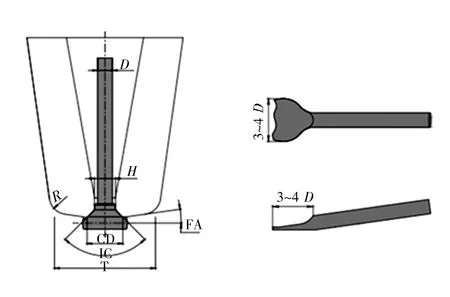
图1 球键合示意图

图2 楔键合示意图

表1 球键合与楔键合的基本特点

2 随机振动仿真

对不同丝径、键合形式和跨度的键合丝进行随机振动仿真，需要联合参数化的三维CAD软件和仿真软件，因此本文采用Pro/E与ANSYS联合进行随机振动仿真。仿真的基本流程如图3所示[6]。

其中，采用族表和关系式实现模型的参数化，并给参数名添加前缀 “DS_”，以便实现模型在Pro/E与ANSYS之间的传递；随机振动激励的步进初值选为0.02 g2/Hz，当激励小于0.1 g2/Hz时步长为0.02 g2/Hz，当激励大于0.1 g2/Hz时步长为0.1 g2/Hz，并且振动激励的方向与键合丝的最大响应应力的方向一致。在键合丝的随机振动仿真过程中，关键是要完成参数化建模、仿真系统搭建、加载并求解3个步骤。

图3 Pro/E与ANSYS联合随机振动仿真流程

2.1 参数化建模

在Pro/E的参数化工具中，族表主要用于参数众多且参数之间耦合度较低的产品族参数化，参数越多，参数化效率越低；而关系式则主要用于参数之间耦合度较高的产品参数化，耦合度越高，效率越高。由于键合丝的形貌和尺寸与丝径、劈刀参数相关，部分参数与丝径耦合，但劈刀属于同类产品族，综合考虑参数化的效率和工作量，本文采用 “族表+关系式”的方式进行键合丝的参数化建模。参数化的具体过程如图4所示，主要为：首先，用族表驱动键合丝的丝径和由劈刀决定的尺寸参数；然后，根据参数的耦合关系，编辑关系式以实现丝径值驱动与丝径耦合的尺寸参数；最后，实现键合丝的参数化。

由于球键合与楔键合的键合形式不同，键合点形貌差异很大，为了提高参数化效率，在建模时分别对球键合与楔键合进行参数化建模，其结果如图5-6所示。

图4 键合丝参数化过程

图5 Au丝球键合参数化模型

图6 Al-Si丝楔键合参数化模型

图7 随机振动仿真系统

2.2 仿真系统的搭建

随机振动仿真是基于假设随机振动过程为平稳随机过程，并以模态分析为前提，求得模型的各阶模态响应，再采用模态叠加法，求解模型在频域的随机振动响应。一个完整的随机振动仿真系统应如图7所示，主要包含模态分析和随机振动两个子系统，由于要与Pro/E共享变型参数和模型数据，仿真系统中增加了参数设置模块 “Parameter Set”，用于驱动Pro/E实现模型的变形和导入。

2.3 加载并求解

仿真系统搭建好后，需要为仿真模型划分网格，添加材料信息 （如表2所示）、约束关系、振动激励和方向等。本文利用系统自由分网，只对网格疏密采取人为控制，以保证仿真的效率和精度。根据键合丝的实际工作情况，分别在第一、第二焊点与焊盘的接触面上添加固定约束。由于通过对比各个方向同等量级的振动及响应发现，垂直于键合丝所在平面的振动产生的响应最大，因此，本文将该方向设置为振动激励方向。而根据GJB 548B《微电子器件试验方法和程序》中随机振动部分的内容，本文设计了如图8所示的振动仿真激励谱，考虑到产品在实际使用条件下的共振问题，将键合丝的一阶固有频率纳入振动频率范围，在步进仿真中根据振动的量级改变W0、W1，便可实现步进的振动激励。

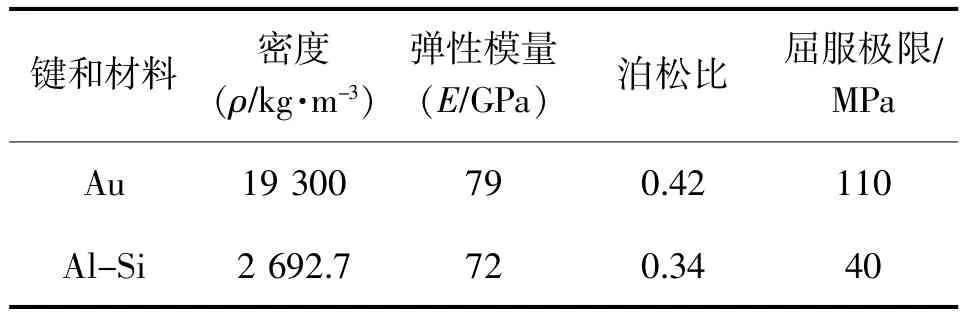
表2 键和丝材料信息

图8 随机振动仿真激励谱

3 仿真结果及分析

由于随机振动的PSD是振动在频域的统计值，因此键合丝所受的振动应力也应是统计值。结合高斯分布和Miner方法，键合丝在振动过程中1、2、3区间应力发生的时间分别占振动时间的68.3%、95.4%和99.73%，假定大于3范围的应力不造成任何损伤，本文将3应力作为键合丝在随机振动仿真中所受的最大应力。

在不考虑键合强度、炭化和腐蚀等因素的影响时，键合丝主要的失效模式有引线脆性断裂和疲劳断裂，而断裂的部位通常是焊点颈部。脆性断裂是由于所受应力过大，超过了键合丝材料的强度极限而发生的断裂失效；疲劳断裂是由于温度、振动等能量在一段时间内的积累超过了某一界限，使键合丝发生屈服疲劳而引起的断裂。这两种应力中，引起疲劳断裂的应力要比引起脆性断裂的应力小得多。因此，在分析仿真结果时应将3应力与键合丝材料的屈服极限进行比较，保证键合丝所受的3应力值小于键合材料的屈服极限值。

通过仿真，获得了键合丝在振动过程中所受的最大应力，其位置在键合点颈部区域 （如图9所示），说明与实际相符。用MATLAB分别仿真数据进行拟合，取安全系数S=1.4并得到如图10-11所示的键合丝所受应力与PSD的对应关系曲线。

图9 键合丝所受最大应力所在位置

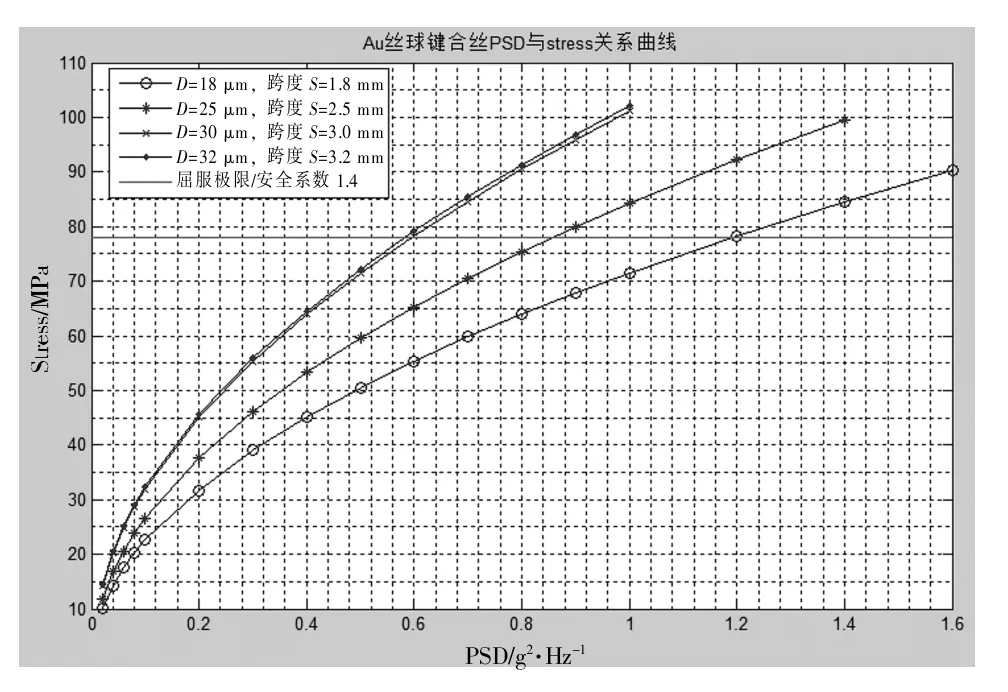
图10 Au丝球键合PSD与振动应力关系曲线

图11 Al-Si丝楔键合PSD与振动应力关系曲

根据图10-11可获得如表3所示的不同键合形式、材料、丝径和跨距的键合丝的极限应力与激励PSD关系表。

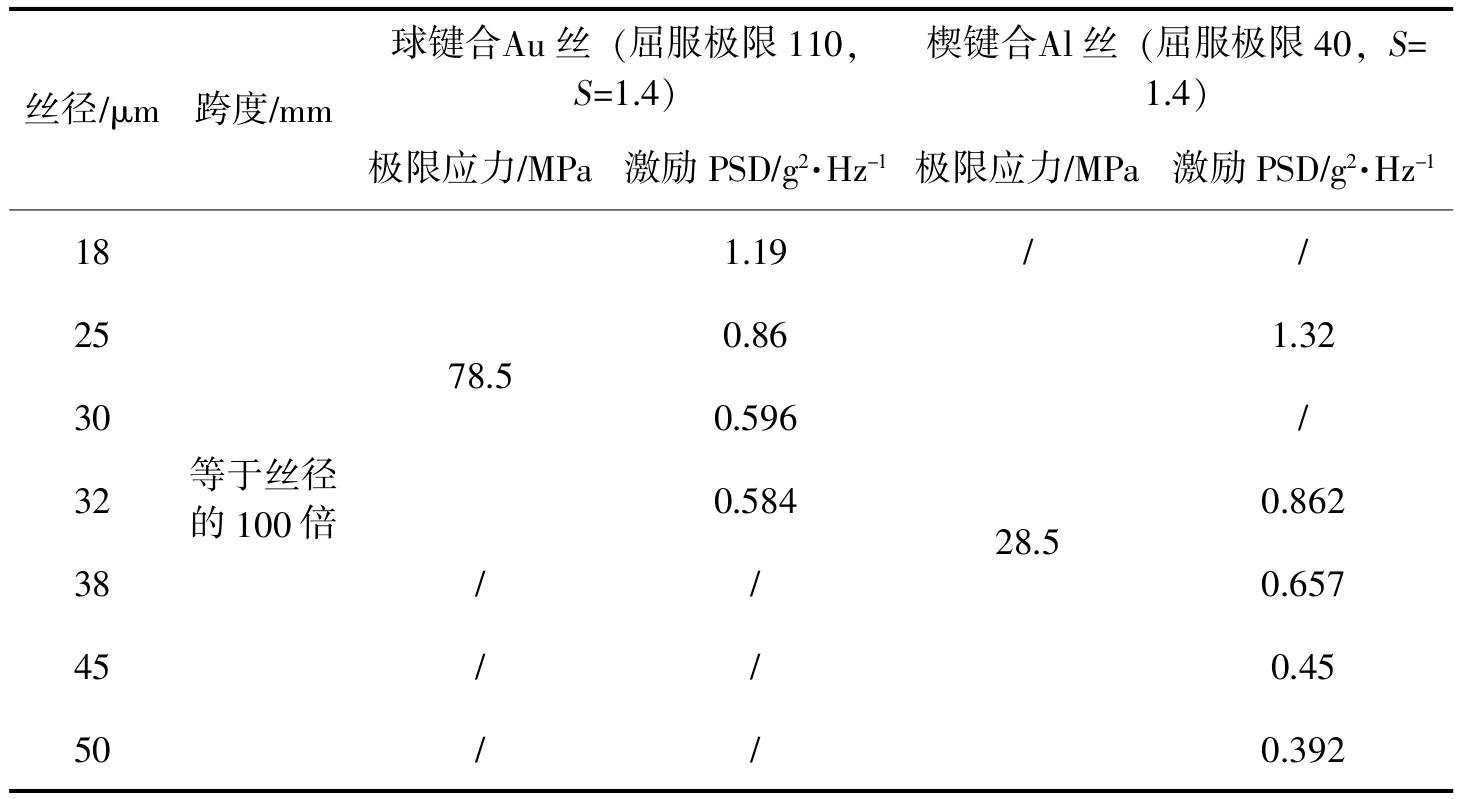
表3 键合丝极限应力及激励PSD表

由表3可知：当材料相同时，丝径越大，跨度越大，能承受的激励PSD越小，此时键合丝跨度成为影响振动承受能力的主要因素；当材料不同而丝径、跨度相同时，Al丝所能承受的PSD大于Au丝所能承受的PSD，因为Au丝的力学性能虽优于Al丝，但Au丝的密度远大于Al丝，从而导致键合Au丝的颈部更容易疲劳。

根据仿真分析结果可知，在进行键合丝设计和选型时需要注意的原则有：首先，应使需键合的焊盘之间的距离尽可能短，从而缩短键合丝的跨度，增大键合丝的耐振能力；其次，在满足电性能和其他特殊条件的前提下，应优先选用Al-Si键合丝，因为在同等跨度下Al-Si丝的振动性能优于Au丝的振动性能；最后，由于大丝径、大跨度的键合丝的振动性能会大幅下降，因此在设计键合点时不能盲目地参照规范要求，应使键合距离小于丝径的100倍，从而使键合丝的振动性能保持在较高的水平。

4 结束语

通过对键合Au丝和Al-Si丝的随机振动仿真分析，本文研究了球键合与楔键合的随机振动性能，拟合了振动应力与激励功率谱密度的关系曲线，获得了不同材料、丝径、键合形式和跨度的键合丝在极限应力下所能承受的激励PSD，上述结果在一定程度上可为键合丝的设计和选型提供参考。

[1]何田.引线键合技术的现状和发展趋势 [J].电子工艺专用设备，2004， 33 （10）： 12-14.

[2]董江，胡蓉.微系统封装内引线键合的可靠性[J].电子工艺技术，2015， 36 （5）： 260-264.

[3]宫在磊，王秀峰，王莉丽.微电子领域中陶瓷劈刀研究与应用进展 [J].材 料 导 报 ， 2015， 29（9）： 89-94.

[4]吕磊.引线键合工艺介绍及质量检验 [J].电子工业专用设备， 2008 （5）： 53-60.

[5]晁雨晴，杨兆建，乔海灵.引线键合技术发展 [J].电子工艺技术，2007，28（4）：205-210.

[6]杨斌.电子设备的随机振动仿真分析 [J].电子工艺技术， 2013， 34 （5）： 299-302.

[7]周桐，张志旭，任万发，等.典型结构振动——加速度综合环境试验研究 [J].装备环境工程，2015，12（5）：50-55.