基于容积卡尔曼滤波的全捷联制导信息估计算法

， ，

(解放军军械工程学院，河北 石家庄 050003)

0 引言

传统的平台式制导弹药在导引头内存在惯性稳定平台，通过万向支架将导引头与弹体运动隔离，避免了弹体姿态对于导引头信息的扰动，且具有较大的视场，但成本高，可靠性低[1]。全捷联制导弹药去掉了万向支架以及稳定平台，具有体积小，质量轻、可靠性高等优点，满足精确制导武器低成本、小型化的特点，逐渐应用于各种“定点打击”式的小规模作战。但由于导引头测量得到的体视线角运动信息是由弹体姿态运动信息与弹目视线角运动信息耦合而成的，不能直接应用于比例导引等导引方法以及控制策略中；并且弹目相对运动模型的非线性程度较高。因此必须寻求合适的滤波算法对弹目视线角及角速度进行准确估计。

目前，国内外学者对捷联制导信息估计问题已经开展了研究，并取得了一定的进展。Vaddi等人针对非线性目标运动模型，利用扩展卡尔曼滤波的方法对目标运动信息进行了估计[2]；Waldamanm等人针对运动模型高非线性特点，采用无迹卡尔曼滤波技术估计弹目视线角速率[3]；Jaipal等人通过对扩展卡尔曼滤波、无迹卡尔曼滤波、中心差分卡尔曼滤波以及粒子滤波在目标跟踪问题中的性能进行了分析，为在实际应用中如何选择非线性滤波器提供了理论依据[4]。李璟璟等人对非线性滤波在量测噪声为高斯和非高斯情形的滤波性能进行了分析，得出了无迹卡尔曼滤波适合于捷联成像导引系统视线角速率估计的结论[5]；孙婷婷等人针对光学导引头不能直接测量体视线角速率问题，利用微分+稳态卡尔曼滤波器估计体视线角速率[6]；林喆等人针对捷联成像寻的器的惯性视线重构问题，提出了一种基于自适应中心差分卡尔曼滤波的惯性视线重构滤波器的设计方案[7]。

上述对于捷联制导信息估计问题的研究都需要利用惯性测量组件对弹体运动信息进行测量，但测量元件精度具有稳定性差、抗干扰能力低等局限性，并且可适用于制导弹药中的测量元件甚少。因此，为满足低成本精确制导弹药小体积、低成本特点，本文提出了基于CKF的全捷联制导信息估计算法。

1 坐标系定义及变换

弹体在飞行过程中与目标形成如图1所示的弹目相对位置关系几何示意图，其中弹体质心位置O为坐标原点，T为目标点，O-XgYgZg为惯性坐标系，OT为弹目视线，其在惯性系下的倾角和偏角分别为qγ和qλ。O′为激光探测器中心位置，OZ为弹轴方向，O′ab平面为激光探测器平面位置，O′a轴与弹体纵向平面重合且与弹轴垂直，O′b轴与O′Za平面垂直，弹目视线在弹体坐标系投影Oc与弹轴O′Z夹角为体视线偏角qα，与弹目视线OT夹角为体视线倾角qβ。OV为弹体的速度矢量，其在惯性系下的倾角和偏角分别为θ和ψv。弹轴OZ在惯性系下形成俯仰角φ、偏航角ψ和滚转角γ。 为便于分析问题，根据图1中弹目视线相对位置关系建立惯性坐标系、弹体坐标系、弹道坐标系、弹目视线坐标系以及体视线坐标系。

如图2(a)中所示，O-XgYgZg为惯性坐标系，坐标系原点O为弹体质心位置，OXg轴沿水平线指向射击方向，OYg轴与OXg轴垂直铅直向上，OZg根据右手法则垂直于OXgYg平面指向右方。O-X2Y2Z2为弹道坐标系，坐标原点O取弹体质心，OX2轴沿速度方向，OY2位于铅垂平面内且与OX2轴垂直向上，OZ2轴与其他两轴垂直并构成右手坐标系。

如图2(b)中所示，O-XbYbZb为弹体坐标系，坐标系原点O为弹体质心位置，OXb轴沿弹体轴线方向，OYb轴在弹体的纵向对称面内且与OXb轴垂直向上，OZb根据右手法则与OXlYl平面垂直指向右方。O-XlYlZl为体视线坐标系，坐标原点O为弹体质心，OXl轴沿弹目视线方向指向目标，OZl轴在弹体系OXbYb平面内且与OXl轴垂直，OYl轴按照右手法则与OXlZl平面垂直向上。

如图2(c)中所示，O-XqYqZq为视线坐标系，坐标原点O为弹体质心，OXq轴沿弹目视线方向指向目标，OZq轴在惯性系OXgZg平面内且与OXq轴垂直，OYq轴按照右手法则与OXqZq平面垂直向上。

上述五种坐标系关系如图3所示，其中qc表示视线坐标系中OYq轴与体视线坐标系中OYl轴之间的夹角，称为视线变换角。L()表示各坐标系之间的转换矩阵。

2 基于CKF的全捷联制导信息估计算法

2.1 滤波模型状态方程建立

2.1.1弹体运动模型

对弹体进行受力分析，将弹体飞行过程中的位置、速度、姿态角作为系统的状态变量Xm(t)=[v,θ,ψv,φ,ψ,γ]T，建立弹体六自由度运动模型[8]。其中，f1(·)表示六自由度非线性微分方程组，ac(t)表示弹体控制指令，w(t)表示风速等扰动因素。

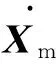
(1)

2.1.2目标运动模型

由于制导弹药打击的目标为陆地目标，因此目标机动具有加速度小且变化缓慢的特点。现采用匀速(CV)运动模型建立如下目标运动模型。其中，vt(0)为目标初始运动速度值，w(t)为随时间变化的扰动值。

vt(t)=vt(0)+wt(t)

(2)

2.1.3弹目相对运动模型

弹目相对运动矢量OT变化规律可利用下式表示：

r=Vm-Vt

(3)

为便于分析弹目视线角的变化规律，将OT用极坐标表示形式表达。将弹体速度矢量OV与目标速度矢量OVt分别投影到视线坐标系OXq、OYq与OZq三轴，根据弹目相对运动角速度与线速度的关系，可得如下弹目相对运动速度表达式[9]。其中，Vx、Vy与Vz为弹体速度在实现坐标系下的投影，Vtx、Vty与Vtz为目标运动速度在视线坐标系下的投影。

(4)

已知弹体速度在弹道坐标系下的坐标为(V,0,0)，为求得弹体速度矢量在视线坐标系下的投影，根据图4中坐标系间的转换关系，可得到惯性系下弹体以及目标的速度矢量在视线坐标系下坐标，如下式：

(5)

将坐标系转换矩阵带到式(5)中，结合式(4)，可得到弹目相对运动速度表达式(6)。

(6)

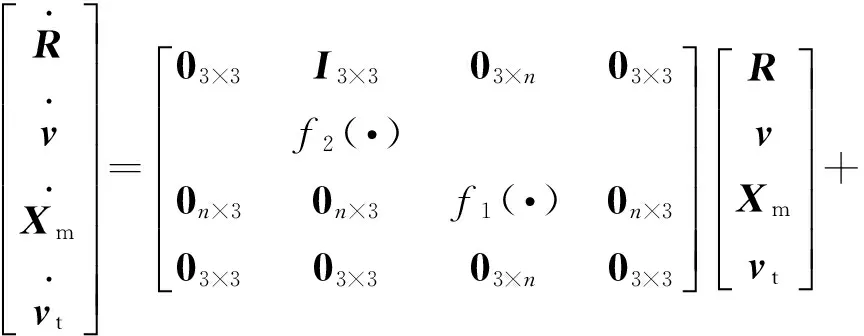
(7)

2.2 滤波模型量测方程建立

将弹目相对距离矢量OT在惯性系下的投影与在弹体坐标系下的投影根据图4中坐标系间的关系进行转换，可得到等式(8)，最终化简得到全捷联导引头量测模型式(9)。其中，Rij为惯性坐标系至弹体坐标系转换矩阵中的元素，v1和v2为导引头量测噪声。

(8)

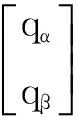
(9)

2.3 容积卡尔曼滤波

卡尔曼滤波是线性条件下的最优滤波，被广泛应用于目标跟踪与状态估计。根据得出的滤波模型可以看到，全捷联制导弹药滤波模型具有高非线性特点，目前解决方法主要有将非线性方程线性化方法与非线性滤波两种方法。由于容积卡尔曼滤波方法不需要求解雅格比矩阵，且滤波精度能达到三阶扩展卡尔曼滤波精度，并且在估计状态变量个数多于3时比无迹卡尔曼滤波能达到更好的收敛效果。因此，本文采用容积卡尔曼滤波方法对弹体运动参数以及弹目视线角进行估计。

容积卡尔曼滤波(Cubature Kalman Filter,CKF)是由Arasaratnam等人于2009年提出[10]。针对无迹卡尔曼滤波(Unscented)在状态变量高维时可能出现滤波发散的问题，Arasaratnam利用球面径向准则来逼近非线性系统的后验分布，带入卡尔曼滤波框架中，最终得到容积卡尔曼滤波。

2.3.1容积卡尔曼滤波初始化

(10)

(11)

2.3.2时间更新方程

1)计算容积点

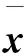
(12)

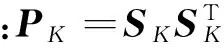
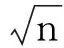
(13)

n表示状态变量的个数，[1]i表示一个全对阵点集。例如，当n=2时，全对阵点集可表示为：

(14)

2)容积点传播

Xi,k+1/k=f(Xi,k/k,uk)

(15)

其中，f()为系统的状态方程。

3)状态预测以及误差协方差

(16)

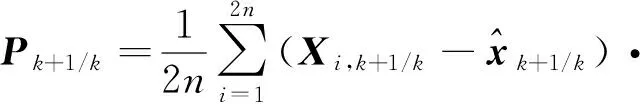
(17)

2.3.3量测更新方程

1)计算容积点

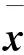
(18)

2)容积点传播

Zi,k+1/k=h(Xi,k+1/k,uk)

(19)

其中，h()为系统的量测方程。

3)量测值估计、量测协方差以及状态量测交叉协方差

(20)

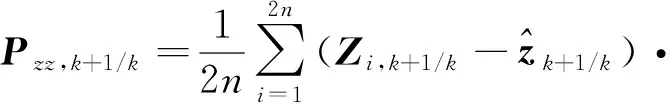
(21)

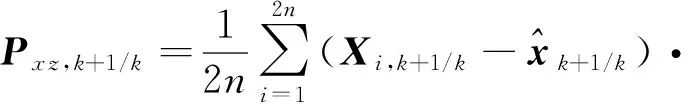
(22)

4)滤波更新方程

(23)

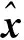
(24)

Pk+1/k+1=Pk+1/k-Kk+1Pzz,k+1/kKk+1T

(25)

结合弹体运动方程、目标运动方程以及弹目视线运动方程，将式(7)与式(9)作为滤波方程的状态方程与量测方程，带入至容积卡尔曼滤波方程式(10)—式(25)中，设置滤波初始值，即导引头开始工作时系统的状态，最终可得到基于CKF的全捷联制导信息估计算法，如图4所示。

3 实验验证

3.1 末段飞行分析

由于弹体在飞行末段飞行速度快，弹目视线角度变化迅速，因此对弹体末段飞行情况以及与目标的遭遇情形进行分析。建立图5所示的弹体末段飞行示意图，图中OXY为惯性坐标系，T为目标点位置。M1、M2以及M3分别为落点小于目标点位置，正中目标点位置以及落点大于目标点位置三种情形下的弹体飞行末段位置，qγ1、qγ2和qγ3分别为弹体飞行末段的弹目视线倾角。如图所示，当弹体落点小于目标点位置，此时的弹目视线倾角始终为锐角并最终趋近于0°；当弹体正中目标，弹目视线倾角最终趋于-90°；但弹体落点大于目标点位置，飞行末端弹目视线角为钝角并最终趋于-180°。

弹体在末段飞行过程中，飞行速度快，并且弹目相对距离减小，导致弹目视线角变化迅速，因此需要滤波器稳定并且满足滤波性能指标。

3.2 数字仿真分析

为验证弹道参数及弹目视线角估计精度以及算法的性能，构建图6所示的仿真验证模型。

由于迫击炮弹在无控段弹道参数基本固定，因此在实验仿真中将容积卡尔曼滤波制导信息估计方法应用在120 mm迫击炮弹道模型中。根据迫击炮弹体气动参数以及实际打靶测得的射击环境构建弹体六自由度运动模型，其中设定发射条件以及风速为扰动因素。根据目标匀速运动模型以及弹体运动模型构建弹目相对运动模型。利用弹体姿态角以及弹目视线角构建导引头模型，将导引头测量得到的体视线角进行滤波得到弹目视线估计角度并通过微分器可得到弹目视线角速率。

由于迫弹在飞行末端速度约为200 m/s，而导引头参测距离约为2 km，导引头工作时间约为10 s，无控迫弹飞行时间约为50 s，因此在滤波初始化阶段，设定导引头在迫弹飞行40 s后打开导引头，为简化问题，假设导引头开始工作即搜索到目标。设定目标点坐标为(1 000,-3.3,0)，目标沿x轴匀速运动速度为10 m/s。滤波模型状态变量初始条件设定为无扰动弹道在40 s时刻的值，将系统噪声都假定为高斯白噪声，考虑弹体初速扰动、射向偏差以及风速扰动，设定滤波器工作时间为10 s进行实验。

3.3 实验结果与分析

按照图示的实验原理进行数字建模并进行实验，实验结果如图7至图10以及表1所示。弹目视线倾角最大误差为8.61°，误差均方根为5.37°；弹目视线偏角最大误差为2.03°，误差均方根为1.11°；弹体俯仰角最大误差为8.59°，误差均方根为5.36°；偏航角最大误差为1.17°，误差均方根为0.14°。从实验结果可以看出，由于设定滤波初始值为无扰动弹道在滤波初始时刻的值，因此在弹体飞行过程中弹目视线角及弹体姿态角估计值会在滤波初始时刻产生最大误差，随着迭代步数的增加，滤波器会使估计值逐渐收敛于真实值。由实验结果可以看出，在弹目视线角变化迅速以及弹体姿态角稳定的情况下，滤波器对于角度的估计值都具有良好的稳定性。由于滤波器设计过程中，建立系统模型存在不确定性以及噪声干扰，导致滤波结果没有完全收敛于真实值，但通过对实验结果的分析，可以看出滤波结果能够满足制导与控制所需信息的精度，并且该非线性滤波器具有一定的稳定性能。因此，该滤波器具有一定的工程应用价值。

表1 估计最大误差及误差均方根Tab.1 Estimated maximum errors and root mean square error

4 结论

本文提出了基于CKF的全捷联制导信息估计算法。该算法通过分析弹目相对运动关系建立滤波模型；针对制导弹药弹道稳定的特点采用容积卡尔曼滤波方法对弹体姿态角以及弹目视线角进行了联合估计。通过仿真验证结果表明，该算法能够满足制导信息精度的要求，并且具有一定的稳定性。本文提出的全捷联制导信息估计方法可为全捷联激光制导技术在制导弹药中的应用提供理论依据。

[1]姚郁, 章国江. 捷联成像制导系统的若干问题探讨[J]. 红外与激光工程, 2006, 35(1): 1-6.

[2]Vaddi S S, Menon P K. Target state estimation for integrated guidance-control of missiles[C]// AIAA Guidance, Navigation and Control Conference and Exhibit. Hilton head, South Carolina: 2007: 1-22.

[3]JacquesWaldmann. Line-of-sight rate estimation and linearizing control of an imaging seeker in a tactical missile guided by proportional navigation[J]. IEEE Transaction on Control Systems Technology, 2002, 10(4): 556-567.

[4]Katkuri J R, Jilkov V P, Li X R.A comparative study of nonlinear filters for target tracking in mixed coordinates[C]// Proc of the 42nd South Eastern Symposium on System Theory. Tyler: Institute of Electrical and Electronics Engineers Inc, 2010: 202-207.

[5]李璟璟. 捷联成像导引头视线角速率估计方法研究[D].哈尔滨: 哈尔滨工程大学, 2008.

[6]孙婷婷, 储海荣, 贾宏光，等. 捷联式光学图像导引头视线角速率估计[J]. 光学学报, 2014, 34(6): 1-7.

[7]林喆, 姚郁, 马克茂. 捷联成像寻的器ACDKF惯性视线重构[J]. 红外与激光工程, 2008, 37(3)：400-405.

[8]韩子鹏等. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2008: 142.

[9]刘义, 赵晶, 冯德军，等.高精度惯导速度信息辅助的弹目相对运动模型构建方法[J]. 电子学报, 2011, 39(9): 2207-2211.

[10]Icnkaran Arasaratnam, Simon Haykin. Cubature kalman filters[J]. IEEE Transactions on Automatic Control，2009, 54(6): 1254-1269.