基于后验量测修正的卡尔曼滤波算法

，，

(解放军电子工程学院，安徽 合肥 230037)

0 引言

卡尔曼滤波是一种递推的线性最小均方误差估计，广泛应用于自动控制、目标跟踪、组合导航等领域[1-5]。标准的卡尔曼滤波器是以精确的数学模型和已知的噪声统计特性为前提，进行递推滤波，取得最优估计的。但在实际工程中，系统的模型参数以及噪声统计特性通常难以获取，导致卡尔曼滤波精度下降，甚至滤波发散[6]。此外，卡尔曼滤波器在状态收敛时，其误差协方差矩阵和增益矩阵趋于极小值，状态改变时，不能及时调整增益矩阵及协方差矩阵，导致滤波器丧失对突变状态的跟踪能力。

针对标准卡尔曼滤波器的不足，目前的改进方式主要分为两类：一是建立合适的估计准则，利用新增的量测信息，对模型的参数和噪声统计特性进行在线调整，实现自适应滤波[7-8]；二是把系统模型及噪声统计特性不准确所带来的误差等效为滤波误差，采用渐消因子抑制滤波器的记忆长度，充分利用当前的量测数据，减小陈旧量测的影响，实现渐消滤波[9]。第二类算法仅需要额外增加一个渐消因子的计算，通过该渐消因子对预测协方差进行修正，间接调整增益，从而增强滤波器的调节能力。由于实现简单，实用性强，得到了广泛应用[10-13]。然而，文献[14]进一步指出，该类算法虽然能较好地解决滤波发散、增强滤波器对突变状态的跟踪能力，但是仍然存在以下缺陷：1)在模型参数及噪声统计特性已知的情况下，渐消因子的引入反而会降低滤波的精度；2)通过渐消因子来增强对当前量测的信任存在修正延后。该文献将引起卡尔曼滤波器发散的原因归结为对状态预测值的不准确，提出对状态预测值进行实时修正，解决了修正延后的问题。但是该算法需要根据经验预先设定一系列的修正参数，存在参数选取困难。针对上述算法的不足，本文提出了基于后验量测修正的卡尔曼滤波算法。

1 目标跟踪建模与修正思路

假设目标的运动状态和量测模型均为线性模型，则离散状态方程和量测方程可以表示为：

xk=Fk-1xk-1+Γk-1vk-1

(1)

zk=Hkxk+wk

(2)

式中，Fk为状态转移矩阵；Hk为量测转移矩阵；Γk为过程噪声分布矩阵；vk、wk为零均值的白色过程噪声和量测噪声序列，其协方差分别为Qk、Rk，且任意时刻vk与wk不相关。由于Fk、Hk、Γk通常为时不变矩阵，故下文统一省略时间下标k，简记为F、H、Γ。

离散时间卡尔曼滤波器的状态预测和状态更新方程为：

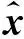
(3)

(4)

式中，Kk+1为滤波增益矩阵。

2 基于后验量测修正的卡尔曼滤波算法(PMKF)

2.1 后验量测卡尔曼滤波(PKF)

为了对卡尔曼滤波器进行修正，本节提出一种利用后验量测进行滤波更新的卡尔曼滤波新算法(PKF)，即利用后验量测zk+1建立对k时刻的状态估计。

将量测方程向前反推一步，把式(1)代入式(2)中有：

zk=Hxk+wk=
H(Fxk-1+Γvk-1)+wk=
HFxk-1+HΓvk-1+wk

(5)

为方便描述，定义

(6)

则新的量测方程可以改写为：

(7)

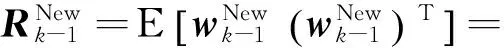
(8)

由于卡尔曼滤波器是线性滤波器，因此，基于后验量测改写后的算法要在卡尔曼滤波器的框架下进行迭代更新，其状态方程与量测方程也必须是线性的。下面，对这一点进行说明。

因为PKF对状态方程没有改动，因此只需要证明其量测方程是线性的即可。

zk+1=Hxk+1+wk+1=
H(Fxk+Γvk)+wk+1=
HFxk+HΓvk+wk+1=
(HF)xk+(HΓvk+wk+1)

(9)

由式(9)可知，由于H、F为时不变的常量矩阵，所以，k时刻的状态xk与后验量测zk+1满足线性关系(HF)，即量测方程是线性的。此外，后面的噪声项等于两个独立的高斯分布经线性变换后求和，仍然为高斯分布。因此，PKF与KF一样，是线性、高斯的，可以在标准的卡尔曼滤波框架下进行滤波更新。

PKF的一个滤波流程为：

步骤1 时间更新

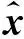
(10)

Pk|k-1=FPk-1|k-1FT+ΓQk-1ΓT

(11)

步骤2 量测更新

(12)

Pk|k=Pk|k-1-Pk|k-1(HNew)T(Sk)-1HNewPk|k-1=

Pk|k-1-Pk|k-1FTHT(Sk)-1HFPk|k-1

(13)

式中：

HFPk|k-1FTHT+HΓQk-1ΓTHT+Rk

(14)

Kk= [Pk|k-1(HNew)T+ΓQk-1ΓTHT](Sk)-1=

(Pk|k-1FTHT+ΓQk-1ΓTHT)(Sk)-1

(15)

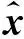
2.2 判决准则

工程应用中，一般根据新息大小计算一个检验量，用于判断滤波是否异常。如果正常，则按一般的滤波步骤进行估计，否则，进行适当的修正。判断滤波异常的判据为[15]：

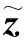
(17)

Pk|k-1=FPk-1|k-1FT+Qk-1

(18)

将式(17)，(18)代入式(16)中，取最严格的收敛判据ε=1，可得

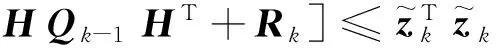
(19)

分析式(19)的左边不难发现，过程噪声协方差Q和量测噪声协方差R分别由目标和观测系统决定，通常不随目标的运动发生显著变化。但是第一项包含反映估计误差的协方差矩阵P，在目标状态改变时，随着跟踪精度下降，P会增大。在目标状态持续性变化，并保持变化强度不变的情况下，P增大，会抬高检测的门限，使得对突变状态的检测能力被削弱。故本文提出，去掉不等式左边第一项，判决条件变为：

(20)

上式左边的物理意义是明确的，为状态噪声和量测噪声的协方差之和。也就是说，在目标状态不发生改变的情况下，量测值偏离真实值的最大误差上限为状态噪声与过程噪声之和，这正好与实际情况相符。如果量测值偏离的程度超过了最大误差上限，只能是目标的状态已经发生改变。因此，利用式(20)作为目标状态改变的判据更加合理。进一步可以发现，当目标状态持续性变化时，由于不等式左边不发生变化，因此对状态突变的检测能力没有下降。

2.3 修正的卡尔曼滤波算法

根据2.1节、2.2节提出的PKF算法和判决准则，基于后验量测修正的卡尔曼滤波算法(PMKF)的修正流程图如图1所示，具体步骤如下。

步骤1：利用zk对k-1时刻的状态和协方差进行标准的卡尔曼滤波更新；

步骤2：进行一步预测，并求取k+1时刻的新息向量；

步骤4：若新息超过判决门限，利用后验量测卡尔曼(PKF)进行滤波更新。否则，直接输出滤波结果；

步骤5：重复步骤1～4。

该修正方法的优势有两点：1)当检测到k+1时刻的目标状态发生改变时，对k时刻的状态进行调整，通过时不变矩阵F的传递，达到修正预测值xk+1|k的目的，解决了修正延后的问题。2)对k时刻的估计值进行修正时利用了量测zk+1，而修正之后进行正常卡尔曼滤波时，再一次用到量测zk+1，即充分利用了新近量测的信息，起到了类似于渐消因子的作用。

3 仿真校验

本文采用匀加速模型，传感器仅提供位置信息。采用均方根误差评价算法的性能，设置了如下四种仿真场景，各种仿真场景下，Monte-Carlo次数1 000次。

表1 场景2目标加速度Tab.1 Target acceleration in scene two

表2 场景3目标转弯角速度Tab.2 Target turning angle acceleration in scene three

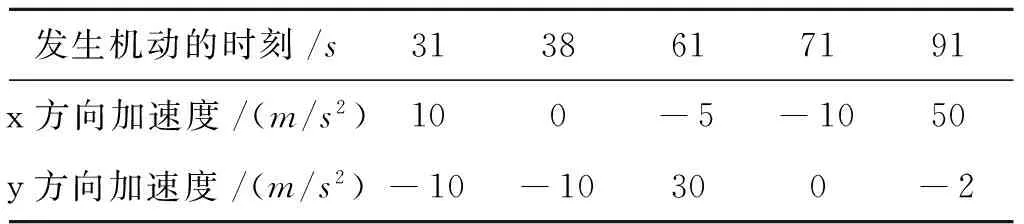
表3 场景4目标加速度Tab.3 Target acceleration in scene four

3.1 仿真实验一

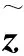
从图中可以看出，文献[14]和本文算法对位置、速度的跟踪精度均有较大的提高，但是本文算法更为优越，尤其是对位置均方根误差的改善尤为明显。然而两种算法对加速度的改善都不大，其原因在于传感器只提供了位置信息，通过位置信息的变化修正速度，再修正加速度，其修正作用逐渐减弱。此外，本文算法在初始状态的收敛速度比标准的KF以及文献[14]略快。

3.2 仿真实验二

利用场景2测试本文算法对加速突变目标的跟踪能力。过程噪声协方差Q=diag[1，1，1]，量测噪声协方差R=100，文献[14]的修正参数同实验一。文献[9]是典型的渐消滤波方法，通过引入渐消因子λ对预测协方差进行修正，进而调节增益矩阵，达到增强滤波器对突变状态的跟踪能力，将其放在相同的场景下进行比较。由于对加速度的改善不明显，仅给出了标准KF、文献[14]、文献[9]以及本文提出的PMKF四种算法的位置及速度估计误差曲线，如图5—图6。

分析图5、图6易知，无论是平稳状态，还是突变状态，本文算法的均方根误差曲线都保持在较低的水平。因此，PMKF对状态突变具有较好的适应能力，相比文献[14]，调节能力更强。文献[9]由于引入了渐消因子，在平稳状态时的跟踪精度略低于标准的KF，但是在目标状态改变时，跟踪精度较KF有明显改善，尤其是变化强度比较大时(体现在最后一次加速度突变)，其跟踪精度甚至好于文献[14]，与本文算法相当。

3.3 仿真实验三

利用场景3测试本文算法在模型不匹配情况下的跟踪能力。各算法均采用匀加速模型跟踪二维场景下的匀速和匀转弯混合运动轨迹。过程噪声协方差Q=diag[1，1，1，1，1，1]，量测噪声协方差R=diag[100 ,100]，文献[14]的修正参数不变。图7—图8给出了该场景下标准KF、文献[14]以及PMKF各算法在x轴和y轴的位置均方根误差。

由图7、图8可知，在模型不匹配的情况下，KF的跟踪精度比较低，尤其是在状态突变的时候，有明显的尖峰。文献[14]通过实时修正，较好地改善了模型不匹配情况下的跟踪精度，状态突变时也具有较强的适应能力，误差曲线相对比较平滑。但是本文算法具有更明显的优势，只在状态突变时有小的波动，较好地克服了模型不匹配的影响。

3.4 仿真实验四

本节主要是对所提出的状态突变的判决准则进行验证。可调白噪声模型是一种典型的通过门限判决来对滤波器进行调整的机动目标跟踪算法，因此，可以用来测试门限的优劣。选取连续强机动目标(场景4)，量测噪声协方差R=diag[100 ,100]，过程噪声协方差在机动时取Q=diag[1，1，1，1，1，1]，非机动时取Q=diag[0.005，0.005，0.005，0.005，0.005，0.005]，原始判决门限和本文判决门限分别由式(19)、式(20)给出。图9—图10给出了两种判决门限下对连续机动目标跟踪的位置、速度均方根误差曲线(此处为x、y误差之和)。

由图9、图10易知，本文提出的判决准则在目标发生连续机动时，由于能较好地保持对机动的检测能力，及时调整滤波器的参数，一定程度上降低了峰值误差，而在非机动段取得与原始算法类似的跟踪精度。因此，本文提出的判决准则更为优越。

通过以上的四个仿真实例，本文所提出的基于后验量测修正的卡尔曼滤波算法(PMKF)主要的优势在于：

1)模型匹配时，通过对滤波器进行微调，提高稳态时的跟踪精度，加快滤波器的收敛速度。

2)在状态发生突变或者模型失配时，利用后验量测进行实时修正，前后两次用到后验量测zk+1，增强了对后验量测的信任度，起到了渐消因子类似的调节作用。

3)与文献[14]的算法相比，克服了经验参数的设定，且对突变状态或模型失配的调节能力更强。

4)在状态连续变化时，所提出的判决准则能保持对状态突变的检测能力，及时修正滤波器，从而取得更高的滤波精度。

4 结论

本文提出了基于后验量测修正的卡尔曼滤波算法。该算法通过对滤波状态进行实时判决，状态平稳时采用卡尔曼滤波，状态突变时采用后验量测卡尔曼滤波算法进行修正。理论分析及仿真结果表明，改进的判决准则能保持对连续突变状态的检测，而后验量测的修正，不仅提高了稳态时的跟踪精度，削弱了状态突变带来的影响，克服了模型失配的缺陷，而且不需要预设修正参数，简单实用，具有一定的工程应用价值。由于卡尔曼滤波器的输出结果由预测项和修正项两部分组成，实际工程应用中完全可以既对预测项进行修正，也对修正项进行调整，以取得更好的滤波结果。如何将二者进行合理融合，形成优势互补是下一步要讨论和研究的课题。

[1]RIGATOS G, SIANO P. Control of heat diffusion in arc welding using differential flatness theory and nonlinear kalman filtering [J]. Intelligent Industrial Systems, 2016, 2(1): 5-19.

[2]YU Y. Consensus-Based distributed mixturekalman filter for maneuvering target tracking in wireless sensor networks [J]. IEEE Transactions on Vehicular Technology, 2016, 65(10): 8669-8681.

[3]ZHU W, WANG W, YUAN G. An improved interacting multiple model filtering algorithm based on the cubature kalman filter for maneuvering target tracking [J]. Sensors, 2016, 16(6): 805.

[4]ZHAO Y. Performance evaluation of CubatureKalman filter in a GPS/IMU tightly-coupled navigation system [J]. Signal Processing, 2016, 119(C): 67-79.

[5]周启帆，张海，王嫣然.一种基于冗余测量的自适应卡尔曼滤波算法[J].航空学报，2015，36(5)：1596-1605.

[6]高伟，李敬春，奔粤阳，等.基于多重渐消因子的自适应卡尔曼滤波器[J].系统工程与电子技术，2014(7)：1405-1409.

[7]SAGE A P, HUSA G W. Adaptive filtering with unknown prior statistics [C] //Proceedings of Joint Automatic Control Conference. US: University of Colorado, 1969: 760-769.

[8]XU T H, NAN J, SUN ZZ. An improved adaptive Sage filter with applications in GEO orbit determination and GPS kinematic positioning[J]. Science China Physics, Mechanics & Astronomy, 2012, 55(5): 892-898.

[9]徐定杰，贺瑞，沈锋，等.基于新息协方差的自适应渐消卡尔曼滤波器[J].系统工程与电子技术，2011，33(12)：2696-2699.

[10]XIA Q, RAO M, YING Y, et al. Adaptive fadingkalman filter with an application [J]. Automatica, 1994, 30(8): 1333-1338.

[11]柯晶，钱积新.基于逻辑切换的改进强跟踪卡尔曼滤波器[J].电子学报，2002，30(6)：925-927.

[12]刘玉磊，冯新喜，鹿传国，等.带渐消因子的Quadrature卡尔曼滤波[J].宇航学报，2013，34(10)：1370-1377.

[13]马云峰.改进的强跟踪卡尔曼滤波器在MSINS/GPS组合导航中的应用研究[J].潍坊学院学报，2014，14(2)：1-5.

[14]杨永建，樊晓光，王晟达，等.基于修正卡尔曼滤波的目标跟踪[J].系统工程与电子技术，2014，36(5)：846-851.

[15]徐景硕，秦永元，彭蓉.自适应卡尔曼滤波器渐消因子选取方法研究[J].系统工程与电子技术，2004，26(11)：1552-1554.