基于二维插值的引信装定器用弹道参数解算方法

，，，

(1.南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094；2.淮海工业集团有限公司，山西 长治 046000)

0 引言

定距空炸引信主要用于打击高机动性和高隐蔽性的有生目标，控制弹丸在目标的上方或侧面起爆，杀伤隐蔽在工事掩体或建筑物后方的目标，在即使无法直接命中情况下也可实现对目标的有效杀伤，大大提高弹药的作战效能[1]。为弹药配备可编程的电子时间引信是实现弹药的定距空炸功能的主要方式之一。

对可编程电子时间引信进行数据装定是实现弹药精确空炸的前提。在已有射表的基础上，可编程电子时间引信根据目标参数、气象参数等与飞行时间的关系实现定距空炸功能。由于每发弹药的作战距离、气象环境、炮口初速等参数不定，每发弹药需要射表中的数据也不尽相同，同时受电子时间引信微处理器存储容量的限制，不可能将整个射表数据存储在引信中,并由引信完成繁琐的插值计算。为了保证弹药的首发命中及电子时间引信的定距空炸精度，需要在弹丸发射前对电子时间引信进行装定[2]。在引信装定器中以一定间隔分化嵌入射表数据，并配合相应的传感器、测距机等设备使用，在弹丸发射前由装定器查表并解算引信需要的数据并实时装定给引信。

二维插值在大气、岩土、图像、地球物理等领域有着广泛的应用[3-8]，尤其是在图像放缩领域中的应用。射表中数据主要是距离和海拔的二维参量，即需要两个参数才能确定所需要的变量。本文针对此问题，提出了基于二维插值算法的引信用装定器弹道参数解算方法。

1 二维插值算法

二元函数插值包括线性插值、Lagrange型二元多项式插值、二元函数的分片低次插值等[9]。二维插值在工程中有着十分广泛的应用，尤其是在数字图像、信号处理和视频处理等领域。

1.1 分片线性插值

分片线性插值是二维插值中最简单的具有连续线性的插值方法。假设已知四个插值点(即矩形的四个顶点，如图1所示)的函数值。

图1中节点的顺序如下：

f1=f(xi,yj) ，

f2=f(xi+1,yj)，

f3=f(xi+1,yj+1)，

f4=f(xi,yj+1)。

在分片线性插值中矩形区域将被分为两个三角形区域：上三角区域和下三角区域。

上三角区域的划分条件及插值函数为：

湖北华贵地处江汉平原，为亚热带季风气候，年平均温度为16.6℃，气候适宜，日照充足，且境内湖泊众多，被称为“百湖之市”。另经国家权威机构测定，洪湖水质达到有机种养的水质标准，有机质含量高，生产条件得天独厚，水产资源极其丰富。洪湖的特色农产品以水产品为主，包括鱼类以及各类水生蔬菜，藕带的栽培基本不使用农药，满足了消费者对健康绿色农产品的追求。在地理位置上，洪湖市紧邻九省通衢的武汉，南靠长江黄金水道，北连荆州，交通运输便利，并与湖北仙桃、监利建成了新农村建设试验区[3]，集聚产业优势和发展潜力。

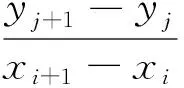
(1)

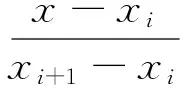
(2)

下三角区域的划分条件及插值函数为：

(3)

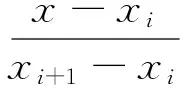
(4)

上三角区为图1中阴影部分1，不包括虚线部分；下三角区域为图1中空白部分2，包括虚线部分。

分片线性插值应用在装定器的弹道解算中需要先判断未知量的所在区域，即判断未知量位于上三角还是下三角区域。

1.2 双线性插值

双线性插值又称为双线性内插，是有两个变量的插值函数的线性插值扩展，核心思想是在两个方向分别进行一次线性插值。图2中节点的顺序同图1的节点顺序。

双线性插值是分片的二次曲面构成的，其插值函数的形式为：

fS(x,y)=(ax+b)(cy+d)

(5)

但由于装定器的弹道解算仅是在每片区域内进行插值，不需要得出实际的函数形式，仅需要在四个离散点组成的区域内进行解算，为此根据上述的双线性插值的思想，得出离散的双线性插值公式为：

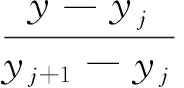
(6)

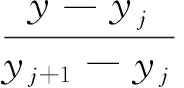
(7)

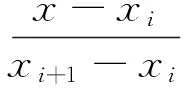
(8)

由式(6)、式(7)、式(8)得：

(9)

2 双线性插值的弹道参数解算方法

由上述的式(2)、式(4)、式(9)可以得出分片线性插值的结果仅与三个节点有关，双线性插值的结果与四个节点相关；双线性插值不必进行判断可以对节点区域内的点进行计算；在插值区域内，双线性插值的结果更加平滑、连续。

在实际的弹道解算中，飞行时间不仅仅是关于射程与海拔的函数，还与气象、炮口初速等相关。因此只能根据射表的数据拟合出计算射表的公式，从而得到插值方法的误差。

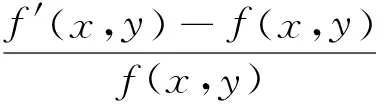
(10)

式(10)中，f′(x,y)为插值函数，f(x,y)为弹道解算出的关于飞行时间的函数，在实际求解误差时通过Matlab得到拟合函数f(x,y)。

根据表1中榴弹的数据拟合出飞行时间函数。

f(x,y)=0.536 8+0.114 3x-0.001 081y

(11)

拟合函数的相关系数R-square=1，误差平方和SSE=6.409×10-6，根据拟合结果可知拟合函数的可信度较高。

由式(11)可知，飞行时间与距离、海拔高度成一次函数关系。分片线性插值的算法与拟合的函数相似程度更高，而双线性插值的算法比拟合的函数多了二次项，因此双线性插值的误差会比分片线性插值的误差大一点。

为了进一步验证分片线性插值与双线性插值在装定器的弹道解算过程中的表现，分别用分片线性插值与双线性插值对表1中的数据进行插值计算，并根据插值计算的结果与表2 海拔340 m处的飞行时间进行误差比较，其中x表示炸点距离，y表示海拔高度。

表1 榴弹的飞行时间Tab.1 Grenade flight time (单位：s)

表2 海拔340 m的飞行时间Tab.2 The flight time of 340 meters above sea level

设A点的坐标为(350,340)，那么根据分片线性插值知A点在上三角区域内，由分片线性插值公式和双线性插值公式得：

fF(350,340)=0.469 078，

fS(350,340)=0.469 31。

由误差公式(10)，分别对两种插值算法进行误差处理：

wF=0.005% ，wS=0.045%。

根据上述比较可知，双线性插值比分片线性插值的精度略差。

在仅考虑插值算法对炸点分布的影响时，若弹丸初速度为800 m/s，炸点距离为350 m，海拔高度为340 m时，分片线性插值的炸点的圆概率误差为0.017 6 m，双线性插值的圆概率误差为0.168 m。由此可以看出双线性插值与分片线性插值的炸点散布相差不大，都可以减小弹丸的空炸炸点散布，但是分片线性插值算法相对更加复杂，计算时间更长。因此在装定器的弹道解算中优先选用双线性插值的二维插值。

根据分片线性与双线性插值的公式可知插值的精度与节点的密度相关。相同海拔高度下不同炸点间隔插值比较如图3，相同炸点距离不同海拔高度间隔插值比较如图4。

分析图3、图4可知，在相同海拔高度下，飞行时间与炸点距离并不是严格的线性关系，炸点距离间隔越小，插值结果精度越高；在相同炸点距离时，飞行时间与海拔高度是严格的线性关系，插值结果对海拔高度间隔不敏感。因此在编制飞行时间射表时，在装定器存储空间允许情况下，炸点距离的间隔应该相应地减小。而相反地，海拔间隔可适当地增加以节省装定器的存储空间。

3 双线性插值算法验证

双线性插值在程序中的应用其流程图如图5。

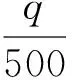
(12)

式中，q=y-yj，p=x-xi。

分别使用根据双线性插值与分片线性插值算法的装定器进行靶场试验，试验数据如表3(F表示分片线性插值算法，S表示双线性插值算法)。

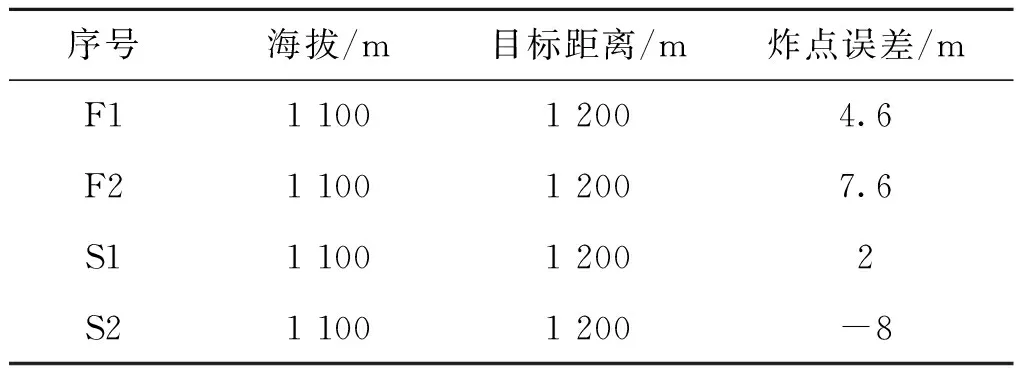
序号海拔/m目标距离/m炸点误差/mF1110012004.6F2110012007.6S1110012002S211001200-8

根据试验数据可知，双线性插值与分片线性插值算法炸点误差都控制在10 m以内，由前文分析知分片线性插值算法的计算更复杂，因此采用双线性插值算法的装定器不仅可以满足解算精度要求，还可以满足解算时间要求。

4 结论

本文提出了基于二维插值的引信装定器用弹道参数解算方法。该方法针对两种二维插值方法进行了比较，得到双线性插值与分片线性插值的解算精度相差无几。分片线性插值算法更繁琐，计算量更大，而双线性插值的计算更为简单，更适用于装定器的弹道解算。在不考虑其他因素的前提下，采用双线性插值的装定器弹道解算比采用分片线性插值节省解算时间，并满足炸点精度的要求。双线性插值的精度与插值节点的间隔密切相关。仿真结果表明，炸点距离间隔对炸点精度影响较大，海拔高度间隔对炸点精度影响较小，在存储容量一定情况下，可以通过减小炸点距离间隔，增大海拔高度间隔来确保炸点精度。实验结果表明双线性插值算法满足解算精度和时间精度要求。

[1]洪黎.单兵火箭弹引信炸点精确控制关键技术研究[D].南京：南京理工大学，2014.

[2]马少杰，张合.空炸引信定距误差分类及修正策略[J].弹道学报，2008，20(3):75-78.

[3]王兆国，程顺有，刘财.地球物理勘探中几种二维插值方法的误差分析[J].吉林大学学报(地球科学版)，2013，43(6)：1997-2004.

[4]刘宇，陈泮勤，张稳，等.一种地面气温的空间插值方法及其误差分析[J].大气科学，2006,30(1)：146-152.

[5]莫林利，赵秀绍，郑伟，等.二维表查找和双线性插值算法的设计与应用[J].华东交通大学学报，2015，32(5):93-98.

[6]王昊京，王建立，王鸣浩，等.采用双线性插值收缩的图像修复方法[J].光学精密工程，2010,18(5)：1234-1241.

[7]舒秀利，周其经，王精业，等.二维插值法在虚拟地形生成中的应用[C]//第四届全国虚拟现实与可视化学术会议论文集.北京：中国系统仿真学会，2009：293-297.

[8]高善清，魏新亮.数字气压高度表数据处理算法分析[J].四川兵工学报，2013,34(7)：80-82.

[9]文世鹏，张明.应用数值分析[M].北京：石油工业出版社，2005.