多约束条件下MIMO雷达自适应波形设计方法

， ，

(解放军电子工程学院，安徽 合肥 230037)

0 引言

多输入多输出(Multiple-input Multiple-output，MIMO)雷达是一种新体制雷达。作为雷达研究领域的一个热点，MIMO雷达以其多输入多输出的特点，在信号形式及系统构成的灵活性、易扩展性等方面有着自身的优势。MIMO雷达的概念一经提出，便引起了国内外学者的兴趣并对其展开了大量的研究[1-9]。文献[7]最早将互信息(Mutual Information，MI)作为波形优化准则，引入到雷达的波形设计中。此后，基于信息论方法的波形设计受到广泛关注。文献[8]从信息论的角度，基于MI与最小均方误差(Minimum Mean Square Error，MMSE) 准则对MIMO雷达正交波形进行了研究。文献[9]研究了有色噪声背景下MIMO雷达的最大互信息波形设计方法。

目标估计是雷达的重要任务之一，目前面向目标估计的自适应波形优化研究主要是MMSE和MI准则下的任意波形设计理论，但如果考虑实际雷达系统的应用需求，特别是低信噪比(Signal to Noise Ratio，SNR) 场景下，仅仅针对目标估计性能的波形设计不一定能满足系统对目标检测性能的要求。然而，目标检测性能是雷达系统进行其他探测任务的重要前提；因此，在针对目标估计的波形优化问题中需将目标检测性能作为重要约束条件加以考虑，使雷达在提高目标估计性能的同时能够兼顾检测性能，满足实际系统的需求。文献[10]以检测性能为约束条件，提出基于凸优化和随机化方法相结合的面向目标估计的波形优化方法；文献[11]以目标检测性能和能量作为约束条件，通过混合罚函数的方法对模型进行求解。然而，以上两种方法都是在白噪声的背景下研究单输入单输出(Single-input Single-output，SISO)雷达的波形设计问题，没有考虑色噪声对问题求解的影响，且都是从频域的角度进行分析，将所求优化波形从频域变换到时域时，会带来性能的下降。本文根据上述问题，提出了多约束条件下MIMO雷达自适应波形设计方法。

1 MIMO雷达信号模型

假设MIMO雷达的发射阵元和接收阵元个数分别为P和Q，其系统模型如图1所示。不失一般性，认为此模型为基带离散时间模型。对于一个距离扩展目标，用一个v阶的有限冲激响应(Finite Impulse Response，FIR)系统描述从第p个发射阵元到第q个接收阵元之间的信号传输，则第q个接收阵元的接收波形可以表示为：

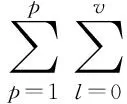
(1)

式中，xp(·)表示第p个发射阵元的发射信号，g(p,q)(·)表示第p个发射阵元到第q个接收阵元之间系统的冲激响应，nq(·)表示第q个接收阵元的加性噪声。

假设L为发射信号长度，且L>v，则式(1)可表示为以下矩阵-向量形式：

(2)

式(2)中，gp,q=[gp,q(0)…g(p,q)(v)]T，yq=[yq(k)…yq(k+L-1)]T，nq=[nq(k)…nq(k+L-1)]T，[·]T代表转置。另外，Xp为一个包含第p个发射阵元波形信息的L×M(M=v+1)Toeplitz矩阵，其矩阵结构为：

(3)

(4)

(5)

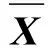
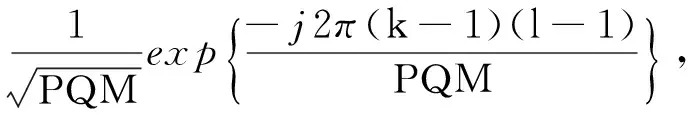
(6)

综上可知，接收回波信号与目标的MI可表示为[7]：

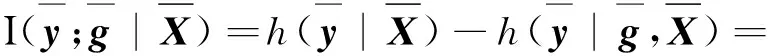
(7)

式中，h(·)表示信息熵。考虑矩阵求逆引理：

det(Ir+AB)=det(It+BA)

(8)

式中，矩阵A∈r×t，B∈t×r；I和It分别表示维数为

r和t的单位阵，可得回波与目标间的MI表示为：

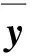
(9)

式中，IQL表示维数为Q×L的单位阵。

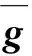
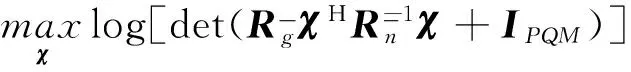
(10)

式中，P0表示发射信号功率。

2 波形设计方法

由于雷达在实际工作场景中往往要同时进行目标检测、估计、识别和跟踪等多项任务，而不仅仅局限于一种任务，因此要求所设计的波形能够使雷达在某一方面获得较优性能的同时，也能够满足其他任务的基本要求。由于在式(10)中并没有SNR约束，因此当环境中存在较强干扰、噪声等影响致使SNR较低时，无法保证设计的波形能够满足目标检测的要求。因此，在进行波形优化时还需要考虑SNR的约束。

根据式(5)，雷达接收端的SNR为：

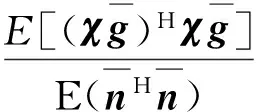
(11)

综上考虑目标函数以及各种约束条件，该优化问题的数学表达形式可表述为：

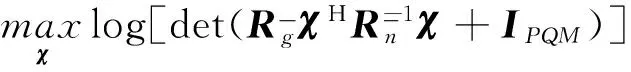
(12)

式中，r表示满足检测性能要求的最低SNR。

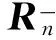
2.1 白噪声假设下的波形设计

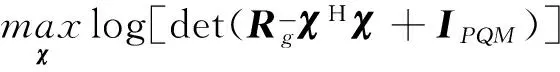
(13)

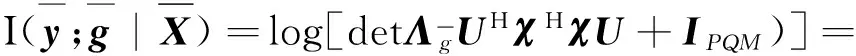
(14)

式中，Z=χU。由于U为酉阵，可以得到tr(χHχ)=tr(ZHZ)。假设所分析的MIMO雷达的波形具有正交性，可以得到χHχ为对角阵。同时可知，ZHZ也为对角阵且对角元素非负。令Q=ZHZ，Qii≥0，∀i∈[1,PQM]，此时将Q作为求解变量，式(13)的优化问题可表示为：

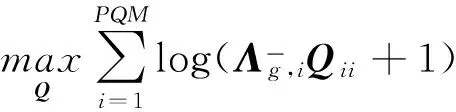
(15)

式中，由于Q为半正定矩阵，式(15)也就变成了一个半正定规划(Semi Definite Program, SDP)问题，该问题有成熟的求解方法，实际使用中有相应的工具箱。设Qopt为式(15)的最优解，则矩阵Z可以表示为[8]:

(16)

其中，Ψ≈LQ×PQM，且列向量之间相互正交，满足ΨHΨ=IPQM。由此，可以得到白噪声假设下所设计的优化波形为：

(17)

2.2 色噪声假设下的波形设计

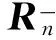
由式(8)和式(9)可知，目标函数可以表示为：

(18)

(19)

log[det(BBH+ILQ)]

(20)

根据Hadamard不等式[12]，有：

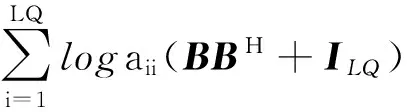
(21)

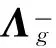
(22)

因此发射波形矩阵需满足：

(23)

式中，Λχ=diag(Λχ,1…Λχ，PQM)；0(QL-PQM)×PQM表示维数为(QL-PQM)×PQM的全零矩阵。综述所述，当波形矩阵满足式(23)所示结构时，式(18)所示目标函数取得最大值。此时考虑两个约束条件的限制，将式(23)代入式(20)和式(12)，则优化问题变为：

(24)

其中第1个约束条件为能量约束，第2个约束条件为SNR约束。式(24)是一个SDP问题，可以使用CVX工具箱进行有效求解。设Λχopt为式(24)的最优解，则接收回波信号与目标的MI最大为：

(25)

此时，可以得到色噪声下所设计的优化波形为：

(26)

3 仿真与分析

本节主要对算法的有效性进行验证，主要在MIMO雷达信号模型下，对多约束条件的波形优化问题进行仿真分析，仿真实验如下。

3.1 白噪声背景下的波形设计

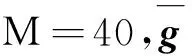
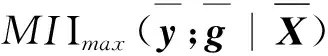
接着，考虑SNR约束对估计性能的影响，假定满足检测性能要求的最低SNRr为5 dB,固定接收信号的观测长度L=80，功率P0在10～100之间变化，则在有无SNR约束条件下优化波形以及线性调频(linear frequency modulation，LFM)信号的MI随P0的变化情况如图4所示，图4(b)是图4(a)的放大。从图4可以看出，在发射功率较低时，SNR约束条件下优化波形的MI明显低于无SNR约束下的优化波形和LFM信号的MI值，这是由于SNR约束对功率分配产生了影响，保证发射波形能够达到限定的检测门限，因而使得MI无法达到最优值；当发射功率增大后，SNR约束下的优化波形的MI值很快超过了LFM信号的MI值；当P0>14时，此时优化波形在获得最大MI值的同时也能够满足检测性能的最低要求，SNR约束将不再起作用，即有SNR约束下的MI值与无SNR约束下的MI值相等。

然后，进一步分析在有无SNR约束下所得到的优化波形对应的检测性能，假设仿真条件不变，有无SNR约束所得波形以及LFM信号对应的SNR随P0的变化情况如图5所示。从图中可以看出，在没有SNR约束下所得波形对应的SNR值在P0较低时低于所设定的门限值，检测性能较差；在有SNR约束下所得波形对应的SNR值在P0较低时也尽可能达到了门限要求，保证了一定的检测性能。随着P0的增大，SNR约束成为了冗余项，不再起作用；而LFM信号的SNR明显低于优化波形的SNR。

最后，分析发射信号到达各目标散射点处的能量分布情况，假设发射总能量在18～55 dB之间变化，其他仿真条件不变 。为方便分析，选取第18,90,120散射点处的能量值以及LFM信号在各散射点处的能量值进行对比分析，如图6、图7所示。

从图中可以看出当发射总能量较少时，能量集中在少数散射点处，大多数散射点处能量极少甚至没有能量；随着发射总能量的增大，各散射点处的能量值也呈增大的趋势，并趋近相同。因此，总发射能量足够大时，本文优化波形在各散射点处的能量分布情况与LFM信号相比将没有区别。同时，对比图6和图7可以发现，图7中第18散射点处的能量值先减小后逐渐增大，这主要是由于在SNR约束下，当发射总能量较小时，发射波形将大部分能量集中在少数散射点(如第18散射点处)处，牺牲MI以提高SNR值，达到检测门限要求；随着发射总能量的增大发射波形将能量逐渐扩散到各散射点处以提高MI，之前能量较大的散射点处的能量会有所下降；当发射总能量增大到一定程度后，使得发射波形可以在获得最大MI的同时满足SNR的要求，SNR约束成为冗余条件，此时随着发射能量的增大各散射点处的能量值逐渐增大并趋近相同。

3.2 色噪声背景下的波形设计

现假设噪声为色噪声，其功率谱密度如图8所示，固定发射功率P0=20，其他仿真条件与3.1相同。图9显示了SNR约束下的优化波形与LFM信号、目标、噪声功率谱密度采样。

观察图9可知，当目标PSD高于噪声PSD时，优化波形的功率较高。反之，优化波形的功率较低。这表明在色噪声情况下，基于MI准则的波形优化能够根据目标和噪声PSD的相对大小自适应地调整波形的发射功率，即在目标特征较明显时分配较多功率，反之分配较少功率。同时，可以看出LFM信号功率不随目标和噪声PSD的大小而发生改变。

4 结论

本文提出了多约束条件下MIMO雷达自适应波形设计方法。该方法在优化设计的过程中，考虑到噪声协方差矩阵对模型求解的影响，将优化模型分为白噪声和色噪声两种情况进行分析。首先将衡量目标检测性能的SNR作为重要的约束条件来保证雷达系统的检测性能；同时，考虑发射信号能量有限的约束条件，采用最大化回波信号和目标间的MI作为优化准则；通过建模，将该非凸的问题转化为标准凸问题进行求解。仿真结果表明，本文所提的优化波形在满足系统检测性能的同时，能最大化目标的估计性能。此外，对于环境背景中存在相关杂波情况下的波形优化设计问题仍需要进一步研究。

[1]Ahmed S, Alouini M. MIMO-radar waveform covariance matrix for high SINR and low side-lobe levels[J]. IEEE Transactions on Signal Processing,2014,62(8):2056-2065.

[2]Ahmed S, Alouini M. MIMO radar transmit beam pattern design without synthesizing the covariance matrix [J]. IEEE Transactions on Signal Processing,2014,62(9):2278-2289.

[3]Chen Y, Nijsure Y, Yuen C, et al. Boussakta adaptive distributed MIMO radar waveform optimization based on mutual information[J]. IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1374-1385.

[4]Tang B, Tang J, Peng Y. Waveform optimization for MIMO radar in colored noise: further results for estimation-oriented criteria[J]. IEEE Transactions on Signal Processing,2012,60(3): 1517-1522.

[5]郑志东,时军学,徐浩彭. 高斯色噪声背景下双基地MIMO雷达的多目标定位[J].探测与控制学报，2016，38(6):68-73.

[6]葛优,刘景萍,赵惠昌,等. 基于正交相位编码信号的MIMO雷达测速测距算法[J].探测与控制学报，2016，38(6):80-83.

[7]Bell M R. Information theory and radar waveform design[J].IEEE Transactions On Information Theory,1993, 39(5):1578-1597.

[8]Yang Y, Blum R S. MIMO radar waveform design based on mutual information and minimum mean-square error estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007,43(1):330-343.

[9]Tang B, Tang J, Peng Y.MIMO radar waveform design in colored noise based on information theory[J].IEEE Transactions on Signal Processing,2010,58(9):4684-4697.

[10]公绪华,谭怀英,袁振涛,等. 检测性能约束下目标估计的波形优化设计[J]. 现代雷达,2014(3):34-39.

[11]谢洪超,李新波,石要武,等. 基于混合罚函数法的认知雷达波形设计[J]. 吉林大学学报(信息科学版)，2015(4):351-355.

[12]Marshall A W, Olkin I. Inequalities: theory of majorization and its applications [M]. New York: Academic, 1979.