刍议线性规划中的一些解决策略

江苏省南京田家炳高级中学 曾榆茗

刍议线性规划中的一些解决策略

江苏省南京田家炳高级中学 曾榆茗

提到线性规划，不少同学认为这类题目较为基础、简单，一旦出现此类题目，分数便是囊中之物。然而，一旦题目稍有一些刁难，不少同学便会掉进陷阱中，接下来，我们来谈一谈线性规划中常见的一些模型以及各类模型相对应的解决策略。

一、“X+Y”模型

例 1 已 知 等 差 数 列 {an}中， 首 项 a1＞0， 公 差 d＞0， 若a1+a2≤60，a2+a3≤100，则5a1+a5的最大值为_______。

分析：很多同学会产生疑惑，数列的题目和线性规划有什么关联？但是当我们开始尝试解答时，我们就会发现其中的道理。

解：由题意，∵a1+a2≤60， a2+a3≤100且{an}为等差数列，a1＞0，d＞0，

∴2a1+d≤60，2a1+3d≤100，a1＞ 0，d＞0，

令 a1=x， d=y，

我们可以画出可行域：

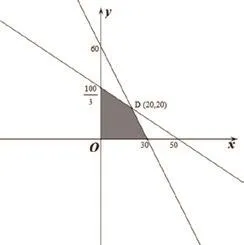
∴当6x+4y=t经过D（20，20）时，t的最大值为200。

∴5a1+a5的最大值为200。

总结：通过这一题，我们可以发现线性规划不仅适用于函数问题，同时在数列问题上也有它们的影子，而所谓的“X+Y”模型的线性规划通常是直接写出它们的表达式，画出它们的可行域进行求解。

二、“XY”模型

例2 在正项等比数列{an}中，若a1≥1，a2≤2，a3≥3，则a4的取值范围是_________。

分析：有了例1的经验，我们很容易根据题目条件得到下列关系：解∵a1≥1，a2≤2，a3≥3，

∴a1≥1，a1·q≤2， a1q2≥3。

令a1=x q=y，

∴目标函数：xy3=t。

到了这一步应该都没有什么问题，但是接下来许多同学就开始不知所措了，因为我们无法准确地画出可行域，但是根据例1，我们能得到一些启发：虽然我们不会画关于“XY”模型的图象，但是我们可以想办法将我们不熟悉的模型转化为我们熟悉的模型，也就是说将“XY”模型转变为“X+Y”模型再进行解答，所以我们想到了左右同时取对数进行求解。

解：∵a1≥1，a2≤2，a3≥3，

∴a1≥1，a1·q≤2， a1q2≥3。

令a1=x q=y，

将不等式组左右两边同时取对数，我们得到

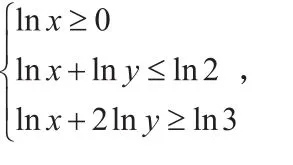
令lnx=m，lny=n，

由此，我们可以画出它的可行域：

总结：当我们面对关于“XY”模型的线性规划时，我们通常将我们不熟悉的“XY”模型转化为我们所熟悉的“X+Y”模型，通常可以采用左右取对数的做法，然后再根据“X+Y”模型画出可行域进行解答。

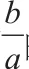
分析：有了前两题的经验，对于这道题我们很容易上手：

解：∵5c-3a≤b≤4 c-a，

∴令b为y，a为x，

我们可以画出可行域进行求解，但面对clnb≥a+clnc这样的条件，我们很容易转化为但是下面许多同学就无法继续进行了，因为我们得到的条件与我们所要求的条件并没有什么太大的关联，但是，当我们细心观察，我们还是可以发现其中的突破口：因为题目要求的是但是我们的条件是关于的，而因此我们可以

解：∵5c－3a≤b≤4c-a，∴令b为y，a为x，

我们可以画出可行域：

∴ lny≥ x。

∴ y≥ ex，x ∈

通过今天的学习，我们会发现小小的线性规划也会有千变万化的题目，但只要我们掌握了其中的方法，将三种模型的解题思路牢记于心，所有的题目都可以迎刃而解！