空间向量在立体几何中的应用

山东省济宁一中高三（4）班 车 畅

高中数学二期课改新教材引入了直线的方向向量及平面的法向量，这一引进对解决空间问题提供了一个很方便、很实用的工具。向量学习的目的之一是“重点培养学生使用向量代数方法解决立体几何问题的能力”，将几何题中的逻辑推理转化为向量的代数运算，沟通代数与几何之间的联系，使问题解决显得模式化、程序化，减少辅助线的添加，降低解题难度。

下面就如何求空间的角、空间的距离、证明平行与垂直这些问题进行详细的论述。

一、证明线面平行或垂直

证明线面平行，可转化为证明直线的方向向量与平面的法向量垂直；证明线面垂直，可转化为证明直线的方向向量与平面的法向量平行，从而得出结论，达到解决问题的目的。

例1 已知正方体ABCD—A1B1C1D1的棱长为2，E、F、G分别是BC、CD和CC1的中心，求证：（1）AD1∥平面EFG。（2）A1C⊥平面EFG。

图1

证明：以D为坐标原点，建立如图1所示的空间直角坐标系D—xyz，则有：D（0，0，0），A（2，0，0），Al（2，0，2），Dl（0，0，2），C（0，2，0），C1（0，2，2），E（1，2，0），F（0，1，0），G（0，2，1）。

令x=1，则

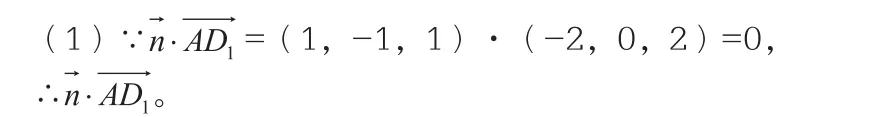
二、用空间向量求角

求平面向量的法向量：设平面α的法向量为n=（x，y，z），利用n与平面内的两个不共线向量a，b垂直，其数量积为零，从而列出两个三元一次方程组，联立后取其一解，即为平面α的一个法向量。

1.求异面直线所成角

设a，b分别为异面直线l1与l2的方向向量，则l1与l2所成角θ的余弦值为：

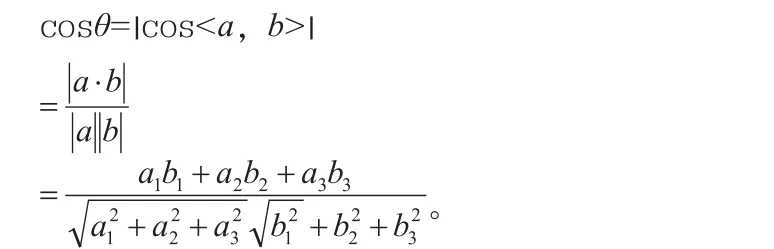
因为异面直线所成角不大于90°，所以其余弦值取非负值。

2.求直线和平面所成角

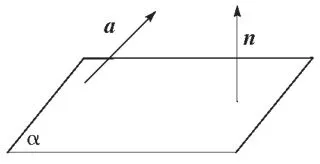
图2

如图2，设平面α的法向量为n=（x，y，z），向量a是直线l的方向向量，则向量a与向量n所成角的余弦值为

又直线l与平面α所成角为向量a与法向量n所成角的余角，故其值为

3.求二面角

（1）如图3，若AB，CD分别是二面角α-l-β的两个面内与l垂直的异面直线，则二面角α-l-β的平面角为所求角的余弦函数值为：

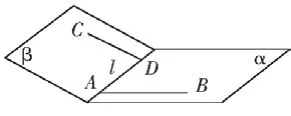
图3

（2）如图4，若n1，n2分别为二面角α-l-β的两个半面的法向量，则角＜n1，n2＞或其补角为二面角的平面角，且

图4

确定方法：

从二面角内看，当法向量n1，n2的方向在二面角内，一个指向平面，另一个背离平面时，向量n1，n2的夹角即为二面角的平面角；当两个法向量或都指向平面或都背离平面时，二面角为向量n1，n2的夹角的补角。

三、用空间向量求距离

1.点到平面的距离

求点A到平面α的距离，可在平面内任取一点B（如图5）。设n为平面α的法向量，则向量在向量n方向上的投影的绝对值即为点A到平面α的距离：

图5

2.直线到平面的距离

如图6，已知直线l与平面α平行，在直线l上任取一点A，求此点到平面的距离可在平面内任取一点B，设n为平面α的法向量，则向量在向量n方向上的投影的绝对值即为点A到平面α的距离：

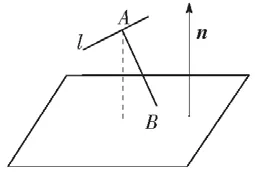
图6

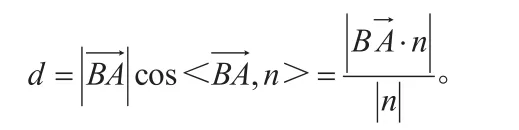
3.两平行平面间的距离

四、利用空间向量证明平行和垂直

对于空间的直线、平面间的平行与垂直的证明问题，需要建立空间直角坐标系，确定出直线的方向向量、平面的法向量，利用向量间的关系来判断空间的直线与直线、直线与平面、平面与平面的平行与垂直问题。

1.直线与直线的平行和垂直

设直线a，b的方向向量分别为a，b，则证明两直线平行的充要条件是它们的方向向量共线，即：

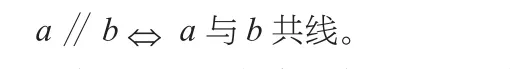
两条直线垂直的充要条件是它们的方向向量互相垂直，即

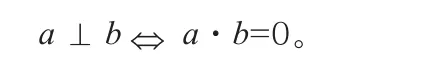
2.直线和平面的平行和垂直

设直线l的方向向量为l，平面α的法向量为n，则直线与平面平行的充要条件是直线的方向向量和平面的法向量垂直，即：

直线与平面垂直的充要条件是直线l的方向向量l和平面的法向量共线，即：

3.平面与平面的平行与垂直

设平面α与平面β的法向量分别为a和b，则平面α与平面β平行的充要条件是两个平面的法向量共线，即：平面α与平面β垂直的充要条件是两个平面的法向量垂直，即

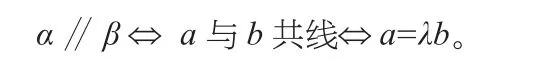
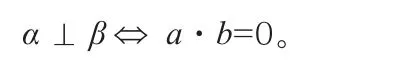
如图7，已知空间四边形ABCD中，AB=AD=CD=BD=2，且点A在平面BCD内的射影恰好落在BC上。（1）求二面角A-BD-C的度数；（2）求异面直线AB与CD所成的角。

解：（1）设点A在平面BCD内的射影为E，BD的中点为F。

所以EF为线段BD的中垂线。

又因为在△BDC中，

图7

所以∠BDC=90°，即DC⊥BD。

又因为点E在BC上，所以E为BC的中点。

以D为原点，DB，DC所在的直线分别为x、y轴，过D且垂直于平面BDC的直线为z轴，建立空间直角坐标系（如图8），则：D（0，0，0）、B（2，0，0），C（0，2，0）。

图8

设BC的中点为E，BD的中点为F，连接AE、EF。

因为在Rt△ABE中，故所以点所以

设平面ABD的法向量为n=（x，y，z），

又平面BCD的法向量为m=（0，0，1），

所以二面角A-BD-C的度数为60°。

所以异面直线AB与CD所成的角为

从上例可以看出，引入空间向量后，避开了复杂的逻辑推理过程，通过建立空间直角坐标系使几何问题代数化，大大降低了空间思维量，降低了问题的难度。