滚转导弹解耦过载驾驶仪及其BP自适应调度法

彭 博,王 伟,王 江,胡欧磊,韩丁丁

(北京理工大学,北京 100081)

0 引言

采用滚转体制的导弹与非滚转导弹相比，具有减小推力偏心、简化控制系统、降低武器成本等作用。因此，滚转导弹在未来具有很大的应用前景[1]。滚转导弹由于受到马格努斯效应和陀螺效应的影响，在俯仰通道和偏航通道存在不可忽视的气动耦合和惯性耦合，且由于导弹旋转及舵机系统的动力学滞后，控制耦合同样无法避免，传统的三回路驾驶仪的动态性能良好[2-4]，但无法消除耦合效应。因此，对于实现精确制导的滚转导弹，需要对基于传统方法的过载驾驶仪进行解耦设计。本文采用传统的滚转导弹动力学建模方法，将滚转导弹在某一特征点处进行线性化。针对线性系统的解耦控制方法，通常分为基于状态反馈的静态解耦和动态解耦[5]，本文通过设计动态解耦算法实现滚转导弹的完全解耦，即俯仰通道与偏航通道完全独立。传统的过载驾驶仪需要加速度计测量过载作为状态反馈量[4,6]。本文针对具有双轴速率陀螺、姿态陀螺和GPS系统的滚转导弹，在没有过载量作为状态反馈的情况下，进行动态解耦过载驾驶仪的设计，弥补了三回路驾驶仪的不足。

导弹在实际飞行过程中，其气动参数是时变的，其动力学模型也是时变的。滚转导弹这种特性尤为明显，其速度高、气动参数非线性特性明显，基于单一特征点处设计的解耦控制器参数无法适应制导段飞行全包络线。工程上常采用基于插值增益调度辅助解耦控制的方法[1]，但该方法需要预先计算的特征点数量较多。在特征点较少，滚转导弹气动非线性特性较强时，通过插值计算出的反馈增益精度不高[7]。一些非线性解耦算法如动态逆解耦算法、H∞鲁棒变增益算法[8-10]等，相比线性解耦算法，算法设计过程较复杂，需要模型精度高，计算量大[11]。本文基于设计的线性动态解耦算法，并结合BP神经网络提出一种BP自适应调度法(BPASM)，计算量较小，尤其在滚转导弹气动参数变化剧烈、非线性特性较强时，控制器参数精度更高，实时解耦效果更明显。取若干组特征点处的飞行状态作为样本输入，动态解耦控制器参数作为样本输出，训练出BPASM的网络模型。该模型可存储在滚转导弹的弹载计算机中，在制导控制段根据不同的飞行状态，计算相应的解耦控制器参数，实现实时动态解耦，具有在线计算量小、速度快的特点，可实现滚转导弹大空域全飞行包络线内的解耦控制器设计，具有一定的工程指导意义。

1 动力学模型及解耦过载驾驶仪设计

1.1 比例式舵机动力学模型

滚转导弹为了实现俯仰和偏航的双通道控制，往往采用两套比例式舵机作为执行机构，其可看作是一个典型的二阶系统。

(1)

(2)

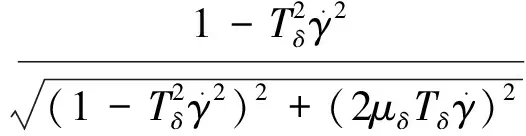
(3)

(4)

1.2 动力学模型

将滚转导弹运动方程组在某一特征点线性化，可得到其动力学模型如下：

(5)

式中α、β为准攻角和准侧滑角；ϑ、ψ为俯仰角和偏航角；δz、δy为俯仰方向舵偏角和偏航方向舵偏角。

(6)

(7)

滚转导弹模型示意图如图1所示。

1.3 动态解耦过载驾驶仪设计

采用一种基于状态反馈的动态解耦算法，该算法可实现状态矩阵对角化[5]，算法描述如下。有状态空间描述的多输入多输出连续时间线性时不变系统：

(8)

其传递函数矩阵描述为

G(s)=C(sI-A)-1B

(9)

控制率取“状态反馈”结合“输入变换”形式，即

u=-Kx+Lv

(10)

输入变换矩阵L为非奇异，即detL≠0。则包含输入变换的状态反馈系统空间描述为

(11)

其传递函数矩阵描述为

GKL(s)=C(sL-A+BK)-1BL

(12)

所谓动态解耦，即是设计输入变换与状态反馈矩阵L、K，使得闭环传递函数矩阵为非奇异对角有理分式矩阵，即

(13)

输入变换与状态反馈矩阵L、K的设计过程如下：

Step 1 计算受控系统{A,B,C}的结构特征量d并计算矩阵E。

(14)

Step 2 计算矩阵F。

(15)

(16)

其中

(17)

Step 4 判断系统能观测性。

(18)

对于完全能观测系统，解耦规范型：

(19)

(21)

根据最小实现变换原理，可导出：

(22)

(23)

(24)

Step 8 对解耦后的各单输入单输出系统指定期望极点组。

{λi1,λi2,… ,λidi +1},i=1,2,…,p

根据极点配置算法，定出状态反馈矩阵各系数：

{ki0,ki1,…,kidi},i=1,2,…,p

Step 9 对原系统{A,B,C}，定出满足动态解耦和期望极点配置的一个输入变换和状态反馈矩阵对{L0,K}。

(25)

Step 10 为满足传递函数闭环增益为1，实现对期望指令的无差跟踪，计算增益矩阵Kω，并得出最终的输入变换矩阵L。

(26)

式中ω1、ω2为期望固有频率。

(27)

(28)

则滚转导弹解耦过载驾驶仪可表示为图2。

2 BP神经网络自适应调度策略

2.1 BP神经网络

若某BP神经网络有n个输入层，p个隐含层，m个输出层，则该网络基本结构形式为n-p-m，其拓扑图如图3所示。

BP神经网络可看成一个非线性函数，网络输入值和预测值分别为该函数的自变量和因变量[12]。神经网络技术已经开始在导弹解耦控制中逐渐应用[13-16]，但BP神经网络在滚转导弹解耦控制中的应用相对较少。

2.2 BPASM算法

在滚转导弹实际飞行过程中，制导控制段往往跨越较大的空域，导弹气动参数变化剧烈，单一特征点处的控制器参数无法适于全弹道，鲁棒性较弱。为解决该缺陷，在弹道包络线内选取多组特征点，降低线性化模型的不确定性，增加系统鲁棒性。传统的插值增益调度法可针对多组特征点，设计相应的反馈增益，运用插值算法，实现控制器与飞行状态的实时匹配，实现实时解耦。然而，由于滚转导弹气动参数非线性特性较强，插值增益调度法需要较多特征点才能够满足一定的精度要求，当特征点不足够多时，该方法的实时解耦能力较差。BP神经网络具有表达非线性系统的能力，当导弹气动非线性较强时，BP神经网络能较好地模拟其特性[13]，可弥补插值算法的不足。本文选取多组特征点处的高度和马赫数作为样本输入，动态解耦控制器L、K作为样本输出，基于BP神经网络设计了BPASM算法，以实现不同飞行状态下解耦过载驾驶仪的实时设计，完成自适应调度。当选取特征点样本数量相同时，相比插值增益调度法，BPASM算法计算量较小，对气动参数非线性拟合度较高，得到的控制器参数精度更高，实时解耦性能更佳。对于尾翼稳定滚转导弹，转速与速度成一定的关系[14]，这里选取滚转导弹实时飞行高度H和马赫数Ma作为输入量，弹上GPS系统可提供二者的实时信息，根据所选特征点离线设计结构为2-6-4的网络f1(H,Ma)计算矩阵L和结构为2-10-8的网络f2(H,Ma)计算矩阵K。该网络根据实时高度及马赫数计算输入变换矩阵L及状态反馈矩阵K，可实现不同状态下的控制系统实时解耦，并满足对期望过载的动态响应要求。该系统原理如图4所示。

3 仿真结果

3.1 动态解耦过载驾驶仪设计

在某滚转导弹制导段选取一处特征点，高度H=3000 m，导弹速度714 m/s，导弹滚转速度为14.3 Hz。此时，滚转弹各动力系数及舵机参数如表1所示。

表1 滚转弹动力系数及舵机参数

该解耦算法可实现过载无静差跟踪，给定期望过载响应指标为超调量不超过1%，调节时间不超过0.1 s。根据指标，令期望二阶系统阻尼比ξ=0.9，自然频率ωm=40，通过动态解耦算法,设计出过载驾驶仪输入变换矩阵L：

输出变换矩阵K：

令俯仰方向过载指令为正负交变矩形脉宽形式，幅值为10g，偏航方向过载指令为0g。将动态解耦过载驾驶仪与传统三回路过载驾驶仪进行对比，设三回路驾驶仪时间常数为0.3 s。有三回路过载驾驶仪与动态解耦过载驾驶仪过载响应对比仿真见图5，偏航角速率对比仿真见图6。

从图5可看出，经典的三回路驾驶仪在存在气动耦合、惯性耦合及控制耦合时，虽仍有较好的动态响应，但俯仰和偏航通道间存在交连，俯仰方向过载指令会引起偏航通道出现约2%的耦合过载响应；动态解耦过载驾驶仪的过载响应超调量为0.15%，调节时间为0.1 s，稳态误差为0，不仅满足设计要求，且完全消除了俯仰通道与偏航通道的交连，不仅如此，传统三回路驾驶仪存在一价惯性环节，响应速度受到限制，而解耦过载驾驶仪的响应速度较快。从图6可看出，三回路驾驶仪的偏航角速率存在峰值约0.9(°)/s的波动，而解耦过载驾驶仪的偏航角速率不存在波动。

令俯仰方向过载指令为5sin(ωt)g的正弦信号，偏航方向过载指令为0，当ω分别取2、3 rad/s时，有三回路过载驾驶仪与动态解耦过载驾驶仪过载响应对比仿真见图7、图8。

从图7、图8可看出，与三回路驾驶仪相比，动态解耦过载驾驶仪可实现对正弦输入的跟踪，并消除了通道间的耦合，动态响应较好。

综上所述，传统三回路驾驶仪存在的耦合作用会对弹体产生不能忽视的控制效果，无法实现与制导系统的匹配；而动态解耦过载驾驶仪将原本含有耦合的滚转导弹动力学系统改造成双通道互不影响的解耦系统，并能进行极点配置满足动态响应。

3.2 BPASM与插值增益调度法的对比

在某滚转导弹制导段选择144组特征点作为样本输入，有12组高度特征点:(200,500,1000,2000, 3000,4000,5000,6000,7000,8000,9000,10 000)，12组马赫数特征点:(0.85,1.19,1.54,1.78,1.80,1.95,1.99, 2.05,2.17,2.33,2.54,3.12)。选取的马赫数存在跨音速段，该组特征点具有较强的气动非线性特性。采用上述解耦算法设计出144组控制器参数L、K作为样本输出，对样本输入输出进行BP网络训练，得到2组BPASM模型f1(H,Ma)，f2(H,Ma)。选取一组非特征点处状态，高度为8500 m，马赫数为1.953 8，验证BPASM算法与传统插值增益调度法的性能。采用BPASM算法，可得到输入变换矩阵L1和状态反馈矩阵K1为

采用传统插值增益调度法可得到输入变换矩阵L2和状态反馈矩阵K2为

将两种解耦控制器参数代入到滚转导弹动力学模型中进行对比分析，令俯仰方向过载指令为正负交变矩形脉宽形式，幅值为10g，偏航方向过载指令为0g。有传统插值增益调度法及BPASM算法过载响应对比仿真见图9，偏航角速率对比见仿真图10。

从图9、图10可看出，导弹气动非线性特性较强时，采用传统插值增益调度策略得到的解耦控制器参数，使得俯仰过载响应存在7.9%的稳态误差，偏航过载响应存在2.1%的稳态误差，偏航角速率存在峰值约0.91(°)/s的波动。采用BPASM算法的解耦控制器使得俯仰过载响应存在0.4%的稳态误差，偏航过载响应存在1.9%的稳态误差，偏航角速率存在峰值约0.36(°)/s的波动。相比之下，BPASM算法使导弹的姿态更加稳定，保证输出过载，实时解耦效果更明显，可以实现与制导系统的匹配。上述仿真表明，传统的插值增益调度法在滚转导弹跨越空域较大、气动非线性特性较强时，实时解耦的动态响应效果较差，BPASM算法可弥补这一缺陷。实时解耦动态效果较好。且BPASM算法只需将网络模型存入弹载计算机中，根据实时飞行状态解算解耦控制器参数即可，在线计算量小，比插值增益调度法具有更大的优势。

令俯仰方向过载指令为5sin(ωt)g的正弦信号，偏航方向过载指令为0，当ω分别取2、3 rad/s时，有插值增益调度法及BPASM算法过载响应对比仿真见图11、图12。

从图11、图12可看出，与插值增益调度法相比，BPASM对正弦输入的跟踪效果更好，通道间的耦合较小，实时解耦的动态响应更佳。因此，当导弹气动非线性较强、特征点数量一定时，BPASM算法实时解耦能力优于插值增益调度法。

4 结论

本文针对滚转导弹俯仰通道和偏航通道间不可忽视的耦合特性，设计一种动态解耦过载驾驶仪，通过状态反馈矩阵K及输入变换矩阵L改造原来的滚转弹体结构，实现了滚转导弹的双通道解耦，且可根据动态响应要求进行极点配置，通过与传统三回路驾驶仪进行对比仿真，说明该过载解耦驾驶仪具有更好的动态性能，实现双通道完全解耦。

滚转导弹制导段跨越的空域较大，导弹速度高、气动非线性特性较强，为实现制导段全飞行包络线内的解耦过载驾驶仪控制器设计，通过设计BPASM算法，根据不同的飞行状态，实时计算出解耦控制器参数，并与传统的插值增益调度法进行了对比，证明该算法在导弹气动非线性特性较强、特征点数量有限时，具有更好的实时解耦效果，在线计算量小，具有较大的工程实用价值。

[1] 李克勇. 旋转导弹制导控制与稳定性问题研究[D]. 北京理工大学, 2014.

[2] Lin D, Fan J, Qi Z, et al. Analysis and improvement of missile three-loop autopilots[J]. 系统工程与电子技术(英文版), 2009,20(4):844-851.

[3] Chu H R, Liu B, Zhang Y. Three-loop autopilot frequency characteristic measurement[J]. Applied Mechanics & Materials, 2014,494-495(5):1332-1334.

[4] 王嘉鑫, 林德福, 祁载康. 战术导弹三回路过载驾驶仪时频特性分析[J]. 兵工学报, 2013,34(7):828-834.

[5] 郑大钟. 线性系统理论(第2版)[M]. 北京：清华大学出版社，2002.

[6] Zarchan P. Tactical and strategic missile guidance, sixth edition[J]. American Institute of Aeronautics & Astronautics Inc, 1990(6):555.

[7] Stilwell D J. State-space interpolation for a gain-scheduled sutopilot[J]. Journal of Guidance Control & Dynamics, 2015,24(3):460-465.

[8] Zhou W, Liang X, Cui Y. Gain-scheduled robust H∞control autopilot designfor a air-to-air missile[J]. Computer Measurement & Control, 2013(1):136-138.

[9] Chen X, Song J. H∞robust gain-scheduled autopilot design for portable missile[C]//中国自动化学会控制理论专业委员会B卷. 2011.

[10] Mahmood A, Kim Y, Park J. Robust H∞autopilot design for agile missile with time-varying parameters [J].Aerospace & Electronic Systems IEEE Transactions on, 2014,50(4):3082-3089.

[11] 贾杰, 刘连章, 曹琦. 导弹解耦控制方法综述[J]. 航空兵器, 2010(3):18-21.

[12] 丛爽. 面向MATLAB工具箱的神经网络理论与应用-(第3版)[M].合肥：中国科学技术大学出版社，2009.

[13] 湛力, 罗喜霜. Matlab神经网络工具箱在导弹解耦控制仿真中的应用[J]. 系统仿真学报, 2006，18(5):1375-1378.

[14] 孙东阳, 易文俊. 基于PID神经网络的滑翔增程制导炮弹解耦控制系统设计[J]. 计算技术与自动化, 2011，30(2):21-25.

[15] Cho D, Kang S, Kim H J, et al. Adaptive dynamic surface control based on neural network for missile autopilot[C]// AIAA Guidance, Navigation, and Control Conference. 2013.

[16] 朱苏朋, 杨军, 罗建军. BP神经网络在导弹控制系统参数整定中的应用研究[J]. 计算机测量与控制, 2010，18(12):2789-2791.