例谈函数教学中的问题情境设计

沈利明

[摘  要] 抽象的函数知识在动画情境、生活情境、故事情境、游戏情境等巧妙的设计与实施中，会展现出令学生容易理解与感悟的知识点与关联，能使学生在各种紧紧围绕课堂教学内容设计的情境中形成更加丰富而深刻的认知、理解、体验与感悟.

[关键词] 函数教学;问题情境;兴趣

引导学生在函数的学习中树立运动、变化的观点，并掌握函数思想与数形结合思想分析问题，使学生在函数的研究中掌握函数的内容、方法与基本应用是函数教学的主要目标. 现实生活中的各种数学问题常包含很多相互联系与影响的变化中的数量，函数这一概念正是对这些变化中的数量关系的描述，因此，教师在函数教学中，应抓住其源于生活的这一显著特点进行各种情境的创设，使学生在熟悉的生活领域里产生与新知识之间的联系，并激发出更加强烈的学习热情.

动画情境的利用

初中生对直观形象的图像、实物投影以及生动的语言描述更感兴趣，因此，教师在函数教学中可以根据学生的这一心理特点，充分利用几何画板进行描点、画图等设计，使学生能够在描点、画图等形成的形象图形中探索函数的性质. 学生在形象的视角下更容易对研究内容产生灵感，函数学习中重要的数形结合思想不仅在这一过程中得到了充分体现，还会让学生在函数的学习过程中掌握一种新的学习策略.

例如，教师教学“分段函数概念”这一内容时，可以引导学生先画出y=x和“招手即停”的规则，并创设生活中的动画情境以加深学生的印象. 如出租车计价问题就是学生比较熟悉的一个例子：某地出台了出租车计价标准，即4 km以内10元（包含4 km）;4 km以外但又在10 km以内的，1.5 元/km，10 km以外的2元/km. 问：

（1）某人打的的行程是8 km，应付车费多少元？

（2）车费和行车里程之间的函数关系式是怎样的？

（3）某人打的共用去35元，行车里程应该是多少千米？

问题（1）就是生活中的事件，对学生来说，解决起来没有问题. 不同的行程会影響车费的不同表达，因此学生对于问题（2）还需要经过一定的思索与研究，其实根据收费标准的三种情况，分段函数的三个关系式自然能表示出来. 对于问题（3），随着函数表达式的呈现，此题也能迎刃而解.

生活情境的利用

学生在函数的学习中如果能够感受到身边的数学，那他们对函数的理解相对来说就会更加轻松. 因此，教师在函数教学中可以充分利用生活情境，以帮助学生探求函数变量之间的关系.

例如，生活中经常会出现市场营销、盈利测算、贷款利息计算等问题，这些都是学生函数学习中可以善加利用的好素材. 教师在函数概念的教学中，如果可以将这些生活中的问题进行妥善设计，并引入学生的实际学习中，那学生对所学内容的理解必然更加到位. 如请学生利用周末时间各自去市场调研某一商品的销售情况，要求如下.

（1）记载某一商品的单价、两组以上的销售数量和金额;

（2）根据自己的调研数据分析单价、数量和金额之间存在的变化规律.

接着，在课堂教学中演示学生的调查结果，并引导学生对其进行分析，使学生能在亲身经历的数据采集与分析中获得常量与变量的概念以及函数的概念.

学生在自己的亲身经历中总结出函数的概念，此时他们心理上的生疏感与陌生感也降低了很多.

故事情境的利用

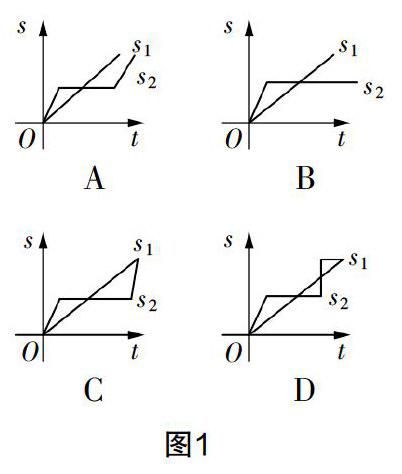
故事情境的巧妙设计与导入往往能使学生得到更多的数学启示. 比如，教师在函数表示法的教学中可以设计这样一个“龟兔赛跑”的故事情境：龟兔赛跑的故事大家都知道，兔子醒来时发现乌龟已经快到终点了，兔子着急得急忙追了过去，但为时已晚，兔子还是输了. 如果我们将兔子与乌龟行走的路程记作s，时间记作t，图1所示的四幅图中哪一个和故事情节是吻合的呢？

游戏情境的利用

紧紧围绕所学内容设计的游戏，也能使学生在趣味性的问题探索中揭示函数的本质.

笔者在一次函数教学中曾经设计了如下游戏：请学生在一副新的扑克牌（王牌除外）中任意抽取一张，并记住自己抽取的牌号，规定A是1，J是11，Q是12，K是13，其他牌号都以扑克上的数值为准，然后请学生按照所得牌号乘2加3后乘5再减去25. 接着，请学生告诉笔者自己的计算结果，笔者可以知道学生原来抽取的牌号.

这是一个运用对应法则的游戏，假设学生抽取的牌号为自变量x，由对应法则可得y=5（2x+3）-25，即y=10x-10，由题意可知定义域为{1，2，3，…，13}，值域为{0，10，20，…，120}，如果算出y=120，那么x=13，即K;如果结果是60，那么x=7. 函数的定义与实质在游戏中充分展现了出来：每个自变量对应的因变量都是唯一的.

探索性情境的利用

布鲁纳曾经说过：“探索是数学的生命线. ”学生的内心常常希望自己在学习中是探索者、研究者与发现者，因此，教师在实际教学中应巧妙地设计一些富有挑战性与探索性的问题情境，以促进学生在学习中深入钻研与探究. 不过，教师在设计这些具有挑战性和开放性的问题时，应考虑到学生的心理特点，并结合教材进行灵活处理，让学生的探索欲望被有力地激发，这样他们才会更加积极地调动思维感受数学，并在经历数学知识的形成过程中体验到成功的乐趣.

例如，笔者曾经设计过这样一个商品销售案例：某商店新购进了一批日用品，该批日用品的单价是16元. 老板根据一段时间的销售试验发现，如果按照每件20元的零售价格出售，每月的销售总量是360件;如果按每件25元的零售价格出售，每月的销售总量是210件. 将每月的销售总量记作y，销售单价记作x，y是x的一次函数.

（1）y和x之间的关系式是怎样的？

（2）如果不存在商品积压以及其他因素，要使每月获利最多，则该批日用品的单价应定为多少？此时每月的最大利润有多少？

分析  此题的自变量是该日用品的销售单价，因变量是每月所获利润，而每月销售总量与销售单价和批发价息息相关，因此，解题的关键在于理清这三者之间的关系.

设计意图  为了让学生更好地理解题目的本质，并更好地解决此题，教师应在教学中引导学生对模型的适用条件与此题的特征进行整理，帮助学生在整理中建构数学模型，引导学生明确运用模型解题时的各个环节与步骤，鼓励学生首先讲一讲哪些应该是先做的，哪些应该是后做的，哪些应该是最后做的，锻炼学生表达能力的同时，使学生对解题思路更加清晰. 教师在学生的讲述过程中，应适时给予评价和点拨，以更好地激发学生的学习热情. 学生在情感上体验当老板的过程时，会不时地产生各种新奇的问题，课堂氛围会因学生的表现而高潮迭起，不同层次的学生还会在体验中均获得很好的感悟.

实践情境的利用

教师在课堂教学中一定要以学生的活动作为教学的主线，并激励学生在课堂上主动参与、实践、思考、探索和创造. 比如，教师教学“正比例函数的图像与性质”时，就可以巧妙地设计操作实践，以促进学生感悟，让学生在正比例函数图像的作图实践过程中掌握“描点法”这一作图方法. 不仅如此，学生还要在自己动手的过程中清楚地知道正比例函数的图像是经过原点的一条直线，接着教师给出典型例题让学生再次进行画函数图像的实践操作，使学生更加明确取两点画函数图像的操作方法以及函数图像的意义. 教师在实际教学中应让学生在活动中动起来，并以实践活动促进学生的知识学习与思维发展，使学生能够在动手操作、实验等数学活动的亲身经历中对数学展开认识与研究，在发现数学、研究数学的过程中锻炼自己的抽象思维能力，从而促进自己从感性认识到理性认识的升华.

函数教学的内容与环节都不止一个，在函数教学的整个阶段，教师应根据每堂课的特点进行各种情境的设计与利用，使学生能在不同情境中对所学内容展开思考与研究，引发学生认知冲突的同时，将学生对新知识的求知欲望与探索热情都充分地激发出来，让学生在各种紧紧围绕课堂教学内容设计的情境体验中形成更加丰富而深刻的认知、理解、体验与感悟.