紧扣三个“读懂”提升课堂效率
聂本桃
《中位数与众数》是北师大版数学教材五年级下册的教学内容,属于“统计与概率”领域。学生在三年级就已学过平均数,理解了平均数的含义,会求一组数据的平均数。本节课的主要内容是让学生在具体问题情境中感受数据的平均水平可以用不同的量来代表,体会平均数、中位数和众数三者的差别。教学中重在对数据的分析,以学生现有知识“平均数”为基础进行延伸教学,又着力于平均数、中位数、众数三者的比较与合理应用以及一组数据的众数和中位数的求法。那么如何读懂教材?如何设计活动?如何读懂学生?采用何种方式?如何读懂课堂中学生的困难与精彩?如何让学生更明白中位数和众数出现的必要性及其作用?如何設计练习让学生更能掌握中位数和众数的求法?
片断一:创设情境,提出问题
师:假如你现在刚刚大学毕业,在找工作时你最关注什么?
生1:工作环境。
生2:有没休息日。
生3:工资。
师:是啊,工资的确是人们在找工作时所关注的一个条件,我也很关心工资。
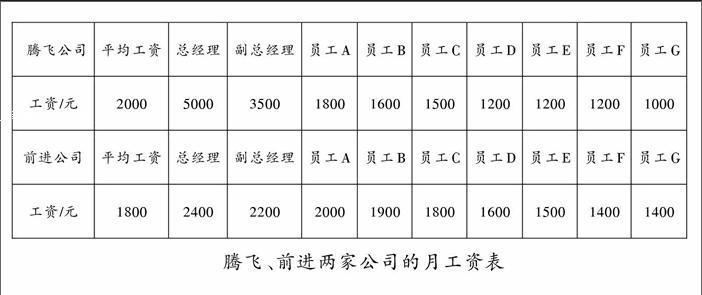
(课件出示两家公司的“平均工资”,腾飞公司:2000元;前进公司:1800元。)
师:你们想到哪家公司去应聘,为什么?
生4:想去腾飞公司,那里工资高些。
生5:想去腾飞公司。
……
师:都想去腾飞公司吗?你们真现实,哪儿钱多就去那儿!
(学生开心地笑了。)
师(出示两家公司的月工资表):请接着观察,再给你一次选择的机会,你会到哪家公司去?为什么?这里的2000和1800分别是腾飞、前进公司这两组数据的“平均数”。为什么腾飞公司所有员工的“平均工资”高于前进公司的“平均工资“?
生6:腾飞公司总经理和副总经理的工资太高了,有5000和3500,比一般员工的工资高得多。
师:是的,由于5000、3500在这组数据中太大,从而使得这一组数据的平均数增大。平均数不能代表这组数据的一般水平。
点评:以“一个骗人的平均数”的情景引入新课,并创造性地使用教材,通过对比引发矛盾冲突,极大地激发了学生的学习兴趣。
片断二:开放质疑,探索新知
师:腾飞公司所有员工工资的“平均工资”不能代表所有员工工资的“一般水平”了,哪个数能代表腾飞公司所有员工工资的一般水平呢?为什么?
(小组讨论,以小组的形式汇报。)
组1:1500能代表这组数据的一般水平,因为它在这组数据的中间。
组2:1200能代表,因为它出现的次数最多。
师:这两个数都有它特定的名称呢!请同学们打开课本第88页,读一读“认一认”部分,把重要的词句做上记号。
……
师:比较两组数据的平均数、中位数和众数,看哪个数据能代表这组数据的一般水平?
生1:两组数据中中位数都能代表本组数据的一般水平。
生2:第一组数据中的平均数不能代表这组数据的一般水平,第二组的平均数能代表。
师:什么时候一组数据的平均数能代表?什么时候不能代表?
生3:一组数据中没有偏大数和偏小数时可以代表,有的话就不能代表。
生4:第一组数据中的众数能代表,第二组数据的众数不能代表。
师:众数在什么情况下能代表本组数据的一般水平?
生5:出现的次数相当多或者在中间位置时。
师:看来“平均数、中位数、众数”能否代表一组数据的一般水平是不固定的,对吗?
生6:“平均数、中位数、众数”能否代表一组数据的一般水平要具体情况具体对待。
点评:层层递进、环环相扣的设问使学生心海波涛翻滚,思维碰撞。同时,让学生小组合作探究出中位数和众数,结合课本,加深理解,并在对比分析中深化理解平均数、中位数和众数的联系与区别,提高了学生根据具体的问题情境选择合理的统计量进行分析决断的能力。这样教学突出了重点,突破了难点,提高了课堂效率。
片断三:分层练习,获取方法
1.找众数。
师:下面是我昨天了解的你们班上部分同学的年龄、身高、体重,得到了三组数据,请你们找出各组数据的众数。
年龄(岁):10 11 12 12 12 11 13
身高(米):1.30 1.50 1.45 1.50 1.45 1.50 1.45
体重(千克):26 28 30 39 25 27 34
生1:第一组的众数是12,因为它出现次数最多,三次。
生2:第二组的众数有两个:1.45和1.50,都出现了三次。
生3:第三组数据没有众数。
师:你们发现一组数据的众数个数有几种情况?
生4:有一个或多个,也可能没有。
2.找中位数。
①出示两组数据,独立思考。
3 12 18 25 27
4 9 17 15 6
师:请同学们找出这两组数据的中位数。
生1:第一组的中位数是18,因为它在最中间。
生2:第二组的中位数是17,因为它在最中间。
师:大家是否都同意?为什么?
生3:不是17,是9。
师:你们认为是哪个?
生4:是9,因为要先排序。
②把前面两组数据的个数变换后找中位数(第一组减一个,第二组加一个变成偶数个)。
3 12 18 25
4 9 17 15 6 13
师:刚才呢?它们的中位数又是哪个?
生1:是12。
生2:是18。
生3:是12或者18?
生4:是15,取12和18的平均数。
师:有了4种答案了。到底是哪个呢?遇到什么困难啦?
生5:这两组数据个数是偶数个,数据是奇数个时,它的中位数好找,数据是偶数个时,它的中位数不好确定。
师:中位数只有一个,且不一定是这组数据中的某一个数。你们认为哪个同学说的有道理?
生6:15。
(课件展示偶數个时找中间的两个数的“平均数”。)
师:第二组的呢?
生7:11。
③找中位数。
这组数据19、23、26、30、A(A不等于其中任何数)的中位数可能是几?
师:有困难了吧,小组讨论。
组1:当A最大时,中位数是26。
组2:当A最小时,中位数是23。
组3:当A<23时,中位数是23;当A>30时,中位数是23时。
组4:当A在最中间时,中位数是A。
小组汇报时,找五个学生拿着上面的五个数字片演示,让学生更清楚地明白道理,达到了课的高潮。
点评:通过有层次、有坡度的练习,让学生通过求众数和中位数,得出众数的特点及求中位数的方法。特别是求中位数时,先设计一组奇数个数据,再在其基础上去掉一个或者增加一个使它变成偶数个数据,注重了学生思维的延续性。最后的一个拓展题,进一步激发了学生的思维,极大地调动了学生的积极性。教师对学生解题结果的处理直观而有趣,将知识与趣味性融为一体,学生学习兴趣盎然,既掌握了中位数和众数的求法,又体会到数学知识的无穷魅力,享受学习成功的喜悦,将整节课推向了高潮。
整体分析
1.读懂教材,创造性地使用教材
新课程理念要求我们用教材教,而不是教教材。教材是提供课堂教学的素材,读懂教材是前提,要求教师深钻教材,弄清教材的重难点,把握教材的关键。这节课的难点是让学生明白平均数有时受本组数据中偏大数或者偏小数的影响,不能代表一组数据的一般水平,意识到中位数和众数出现的必要性,从而找出这组数据的中位数和众数,明白用平均数、中位数和众数能否代表一组数据的一般水平要具体情境具体对待。重点是找到一组数据中众数的特点及求中位数的方法。片断一中将教材中一个超市的工资表,巧妙地改成两个公司招聘普通员工,通过对比分析两组数据主动获取本节课的新知,既激发了学生的兴趣,又突破了难点。随后又巧妙地设计两组练习,水到渠成地突出了本课的重点。
2.读懂学生,从学生的需要出发
读懂学生就是依据学生的兴趣,从学生的生活经验出发,找到学生学习的生长点,设计有效的活动,让学生在活动中自主、合作、探究出新知。学生对找工作时的待遇问题感兴趣,片断一中就从工资多少入手,激发认知冲突;片断二中让学生小组合作,探究中位数和众数,明白中位数和众数产生的必要性,通过对比,明白平均数、中位数和众数能否代表一组数据的一般水平要具体情境具体对待。片断三中通过两组练习,让学生通过求众数和中位数,得出众数的特点及求中位数的方法。求中位数时,通过先设计一组奇数个数据,再在其基础上去掉一个或者增加一个使它变成偶数个数据的方法,使得学生思维具有延续性。
3.读懂课堂,关注学生的精彩和困难
课堂中教师可以从哪些方面关注学生?关注的方法有哪些?如何合理判断学生的想法?如何实施合理的教学对策?笔者认为莫过于两个方面:关注学生学习的“精彩”和“困难”。在片断一中,问学生“想到哪家公司去应聘,为什么?”学生都说:“想去腾飞公司,那里工资高些。”这时教师调侃说“都想去腾飞公司吗?你们真现实,哪儿钱多就去那儿!”全班学生都开心地笑了,教师以其幽默风趣的语言,拉近了师生之间的距离,让课堂变得轻松愉快。在片断三中,教师在学生找到中位数和众数时,在学生找到偶数个数据的中位数时,在学生解决出拓展题时都以热烈的掌声给予鼓励。在学生找中位数和众数,以及做拓展题有困难时,就要求学生小组合作学习:在求偶数个数据的中位数时,学生出现了三种解法,到底哪一种正确呢?这时教师加以点拨“中位数只有一个,可以不是这组数据中的数”,这使学生一下就明白了选哪一个数作为中位数最有道理,同时也知道了求中位数的方法;做拓展题时,遇到困难就采用小组游戏的方式,由五个同学举着这5个数字卡片,依次变换A的位置,使得解题结果的处理直观而有趣,将知识与趣味性融为一体,学生学习兴趣盎然。这样,关注学生的想法,用适当的方法调味。面对学生“精彩”,教师大加赞赏,给予掌声鼓励;面对学生困难时,利用小组合作的学习方式和教师引导点拨,使学生跳一跳也能摘到果子,既激发了学生的学习兴趣,增强了学生学习的信心,又体会到数学知识的无穷魅力,享受学习成功的喜悦,提升了课堂的效率!
(作者单位:恩施市教学研究和教师培训中心)
责任编辑 陈建军

