一种行车和驻车变结构形式的鼓式制动器设计及计算

崔祥波，李彬

（奇瑞汽车股份有限公司 底盘技术研究院，安徽 芜湖 241006）

一种行车和驻车变结构形式的鼓式制动器设计及计算

崔祥波，李彬

（奇瑞汽车股份有限公司 底盘技术研究院，安徽 芜湖 241006）

领从蹄鼓式制动器的特点是：效能因数稳定性高，但效能因数低；双向自增力鼓式制动器的特点是：效能因数稳定性低，但效能因数高。如果能设计一种制动器，它在行车制动时是领从蹄式，利用其效能因数稳定性高的优点，在驻车制动时变为双向自增力式，利用其效能因数高的优点，它将是一种很有应用价值的制动器。本文通过一个实例给出这种制动器的制动力矩计算过程，并指明其设计要点。

领从蹄制动器；自增力制动器；变结构制动器；行车制动；驻车制动

引言

领从蹄鼓式制动器，效能因数稳定性高，易于布置驻车杠杆机构，因此常用于紧凑型乘用车的后轮制动器，同时兼做行车和驻车制动器。自增力鼓式制动器的效能因数稳定性是所有鼓式制动器中最低的，已经很少用作乘用车的行车制动器，但因为它的效能因数是所有鼓式制动器中最高的，所以还常用作单一功能的驻车制动器，比如盘中鼓式后制动器总成中的驻车制动器和中央制动器一般都是自增力式。

领从蹄式制动器兼做驻车制动器时（尤其是7座以上的车），常常有驻车制动效能不足问题（因行车制动时后轮只承担 35%左右的制动力，所以行车制动效能一般都足够），解决这个问题有4种办法：（1）提高驻车杠杆机构的机械效率，（2）增大制动器外径，（3）提高摩擦片的摩擦系数，（4）驻车时变为另一种高效能因数的制动器（比如自增力式）。第一种办法因结构及材料性能的限制，一般无法优化；第二个办法往往因布置空间和成本的限制而不可行；第三种办法会影响行车制动器的效果（因为驻车和行车用的是同一副摩擦片），因此往往也不可行；如果第四种办法能够实现，就能达成如下理想效果：（1）成本增加很少，（2）布置空间不变，（3）摩擦系数不变所以不会影响行车制动，（4）行车制动时是领从蹄式，效能因数稳定，驻车制动时是自增力式，效能因数高，同时满足行车和驻车制动性能要求。

本文研究的某款车后轮制动器，就是这种行车和驻车变结构形式的鼓式制动器。这种制动器的设计计算和设计要点还没有文献进行过研究，也比较复杂，本文以右后制动器为例进行具体的分析计算，其分析计算方法具有普遍适用性，不同结构尺寸的制动器可以参考。

1 制动器结构分析

图1是该右后制动器的二维简图和三维数模，该制动器行车制动和驻车制动使用同一副摩擦片，是一种综合鼓式制动器。行车制动是领从蹄结构，其效能因数的计算在相关文献中有详细论述，本文不再赘述。

图1 右后制动器的二维简图和三维数模

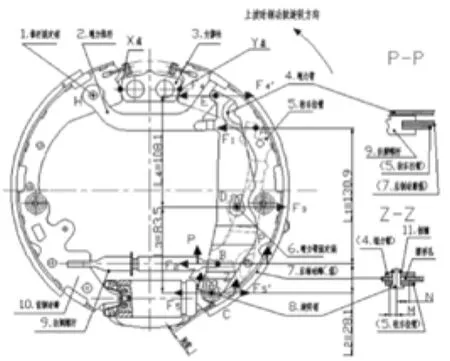
图2 驻车机构各件的装配关系

驻车制动器各件的装配关系见图1和图2（图2是图1旋转180°而成）：后制动蹄7下方有一个驻车拉臂5，上方有一个增力臂4，拉臂和增力臂通过旋转销8形成铰链连接，旋转销8穿过后制动蹄7的蹄筋上的一个腰形孔，并可以在腰形孔中有旋转运动。增力臂4的中间部位通过固定销6固定在（制动蹄的）蹄筋上，增力臂可以绕固定销6旋转。增力臂尾部有个外圆弧，增力推杆2有个内圆弧，两个圆弧配合也形成一个铰链连接（靠一根小弹簧绷紧，见三维数模）。增力推杆2的另一端通过推杆固定销1与前制动蹄形成铰链连接。综上，拉臂、增力臂、增力推杆、（制动蹄的）蹄筋，通过固定销和一根小弹簧形成铰链连接，形成驻车制动的杠杆系。

行车制动效能因数计算，常用图1进行分析。驻车制动效能计算若仍用图1分析，则不容易看出其制动器结构形式，我们将其旋转180°，变为图2，可以看出一个双向自增力结构的雏形，下面详细分析。

1.1 上坡驻车的情况

驻车时制动鼓逆时针旋转。如图2，驻车时，驻车拉臂5在来自驻车拉索的力F1作用下，绕自调螺杆9的支点B旋转，使旋转销8产生绕支点B的旋转位移，旋转销8带动增力臂4绕支点D（即增力臂固定销6）旋转，使增力臂的E点产生绕支点D的旋转位移（在力系平衡状态下，只是一种位移趋势），推动增力推杆2向左移动，并施加给前制动蹄10一个力F4。在 F4以及制动鼓逆时针摩擦旋转力的共同作用下，前制动蹄10脱离支撑块3的左侧支点X。前制动蹄被张开以后，逆时针旋转继而通过自调螺杆推动后制动蹄7绕支点Y形成制动力矩。很显然，此时制动器变成了“带滑动支座的自增力式结构”，前制动蹄10为第一蹄，后制动蹄7为第二蹄，支点Y是最终承力点。

1.2 下坡驻车的情况

驻车时制动鼓顺时针旋转。如图2，驻车时，驻车拉臂5及增力臂4的运动及力系同2.1描述，此时，后制动蹄7在支点D的力F3和制动鼓顺时针摩擦旋转力的共同作用下，脱开右侧支点Y。后制动蹄7被张开以后，顺时针旋转继而通过自调螺杆推动前制动蹄10绕支点X形成制动力矩。很显然，此时制动器变成了“带滑动支座的自增力式结构”，后制动蹄7为第一蹄，前制动蹄10为第二蹄，支点X是最终承力点。

2 驻车制动器效能因数计算

2.1 驻车拉臂及增力臂的各杠杆力系分析计算

如图2，驻车制动时，驻车拉索在驻车拉臂的A点施加力F1，则拉臂在C点施加给旋转销8力F5′，同时在C点受到旋转销的反作用力F5，F5=F5′= (L1/L2)F1=4.658F1。拉臂施加给自调螺杆的力 F2=F1+F5=5.658F1。F5′成为增力臂的促动力，使增力臂在E点产生施加给增力推杆的推力F4，同时增力臂在E点受到增力推杆的反作用力F4′，F4= F4′=（L3/L4)F5′=0.772F5′=3.598 F1。D 点输入 F3=F4′+F5′=10.028 F1。

2.2 上坡驻车时的效能因数计算

2.2.1 上坡时第一蹄的效能因数

如图 3，上坡时制动鼓逆时针旋转，第一蹄是“平行滑动支座式领蹄”，促动力为 F4，输出力为 Fd1，效能因数计算公式相关文献已有详细说明。其效能因数：

图3 上坡时第一蹄的受力分析（图中左侧那个蹄）

式中：

μ—制动衬片的摩擦系数，与行车制动摩擦片一样，本例中μ=0.35；

μs-制动蹄筋和自调螺杆间的摩擦系数，钢对钢为 0.2-0.3，本例取μs=0.25；

c—制动力作用点到中心的距离，mm；

a—中心到滑动支座的距离，mm；

s—中心到滑动平面的距离，mm；

r—制动鼓半径，mm；

θ—制动衬片包角，角度（°）；

θ′—制动衬片包角的弧度值，弧度rad，θ′=θ×π/180°。

代入，得BF1=1.832，也即：

Fd1为第一蹄等效到制动鼓半径上的摩擦力。

所以，Fd1=1.832F4=1.832×3.598 F1=6.59F1,为了便于叠加，全部以F1作为基准来计算效能因数。相对于F1来说，第一蹄的实际效能因数BF1′=6.59。

2.2.2 上坡时第二蹄的效能因数

如图4，第二蹄是“斜面滑动支座式领蹄”，它受到两个促动力，一个是自调螺杆的力 Fax（实际是其分力 F5，详见下面（1）中的论述），一个是增力臂固定销的力F3，两者产生的效能因数叠加，成为第二蹄的总效能因数，下面分别计算。

（1）自调螺杆的力Fax产生的效能因数。根据相关文献可知：

图4 上坡时第二蹄的受力分析（图中右侧那个蹄）

如图4，第二蹄是“斜面滑动支座式领蹄”，其初始效能因数的计算公式同式（1），式中c=71.5，a=98,其它各参数值按图 4计算。其中μs用μs′代替（因支持销有斜度），μs′=μs+tanΨ=0.25+tan17°=0.556。代入计算得：

BF2初始=1.233，即 Fd2=1.233F5，则 Fd2=1.233×11.415F1=14.075F1，所以，第二蹄因自调螺杆产生的实际效能因数BF2螺杆=14.075。

（2）增力臂固定销的力F3产生的效能因数

如图4，第二蹄是“斜面滑动支座式领蹄”，其效能因数计算公式同式（1），只是针对F3计算效能因数时，式中c=16.1，a=98,其它各参数值按图 4计算。其中μs用μs′代替，μs′=μs+tanΨ=0.25+tan17°=0.556。代入计算得：

BF2初始=0.802，即 Fd2=0.802F3，则 Fd2=0.802×10.028 F1=8.042F1，所以，第二蹄因自调螺杆产生的实际效能因数BF2固定销=8.042。

（3）第二蹄的总效能因数

BF2′= BF2螺杆+ BF2固定销=14.075+8.042=22.117。

2.2.3 上坡时总的效能因数

BF总=BF1′+ BF2′=6.59+22.117=28.707。

2.3 下坡驻车时效能因数计算

2.3.1 下坡时第一蹄的效能因数

如图 5，下坡时制动鼓顺时针旋转，第一蹄是“平行滑动支座式领蹄”，它受到的促动力是D点的F3，因为F3处于中心线的下方，所以C值应取负值，BF1的计算公式同式（1）。各参数见图5，代入得BF1= 0.754，即Fd1=0.754F3=0.754×10.028F1=7.561F1，相对于 F1来说，第一蹄的实际效能因数BF1′=7.561。

图5 下坡时第一蹄的受力分析（图中右侧那个蹄）

2.3.2 下坡时第二蹄的效能因数

如图6，第二蹄是“斜面滑动支座式领蹄”，它受到的促动力是自调螺杆的推力F6，F6是两个力的合力，一个来是蹄筋的增力Fax,另一个是驻车拉臂的力F2。

图6 下坡时第二蹄的受力分析（图中左侧那个蹄）

根据相关文献，类同（8）我们得式（9）

其中 c、a值见图 5，c=-16.1，a=71.5，代入得 Fax=1.198F3=1.198×10.028F1=12.009F1。则 F6=Fax+F2=12.009 F1+5.658F1=17.667F1。下面计算由其产生的效能因数。

如图6，第二蹄是“斜面滑动支座式领蹄”，其初始效能因数的计算公式同式（1），式中c=71.5，a=98,其它各参数值按图 6计算。其中μs用μs′代替，μs′=μs+tanΨ=0.25+tan17°=0.556。代入计算得：BF2=1.247，即 Fd2=1.247F6=1.247×17.667F1=22.031F1，相对于F1来说，第二蹄的实际效能因数 BF2′=22.031。

2.3.3 下坡时总的效能因数

BF总=BF1′+ BF2′=7.561+22.031=29.592。

3 结构设计要点（所有参数均在图2中标出）

3.1 增力臂E点的初始位置

驻车时能转换为自增力结构的关键是能将两个蹄中的一个脱离支撑块，这样第一蹄的增力（制动鼓的摩擦力旋转制动蹄形成增力）才能通过自调螺杆传递给第二蹄。实现方法是：增力臂一旦开始动作，这个动作就能立即传递给增力推杆，增力推杆立即将一个蹄推离支撑块。所以增力臂E点的初始位置，应该使增力臂与增力推杆为零间隙或小间隙。

3.2 旋转销8的初始位置

对旋转销的初始位置有两个要求，一是在驻车时，旋转销旋转时不能与蹄筋干涉，要有足够的旋转空间（这个旋转位移大），二是行车制动时，当蹄筋被分泵张开时，蹄筋不能与旋转销干涉（这个旋转位移小）。所以，旋转销应处于腰形孔中间偏M方向，一般N=2～3M。

3.3 蹄筋上的腰形孔尺寸及走向

（1）尺寸。在保证蹄筋有足够强度的前提下，腰形孔越大越好。但因为蹄筋（腰形孔的基体）在此处受空间限制不会太大，所以腰形孔尺寸的设计上限是：蹄筋被掏出一个腰形孔后，在行车制动时仍应有足够的强度和刚度；设计下限是：为避免行车及驻车制动时蹄筋与旋转销干涉，腰形孔应该足够大；(2)走向。腰形走向要沿着制动时旋转销的位移轨迹。

3.4 拉臂的初始位置

从计算过程可以看出，拉臂、蹄筋始终是同时和自调螺杆受力点B接触的，所以拉臂初始位置应满足的条件是：当拉臂和蹄筋同时与自调螺杆接触时，拉臂尾部与蹄片内圆弧仍有间隙。否则，拉臂会将自调螺杆顶起脱离蹄筋，这时螺杆上受到的力就无法传递给蹄筋。

3.5 拉臂（及增力臂）外边缘与蹄片内圆弧的间隙J

间隙J应足够大，应满足的条件是：在制动状态时，拉臂及增力臂（此时已产生旋转位移）仍然与蹄片内圆弧有间隙。若两者发生干涉，拉臂的力就无法通过杠杆机构传递给增力推杆，制动蹄就无法被推离支撑块，制动器就不是自增力结构了。

3.6 增力臂与增力推杆接触部位的表面质量

接触部位表面应光滑平整，这样增力臂的力才能有效传递给增力推杆，若接触面有斜角，则分力会比较大，力和行程的效率损失大。如果用冲裁工艺成型，则光亮带应在70%以上。

3.7 推杆固定销中心H点和圆弧铰链中心E点的关系

两者应处于同一水平线上，目的是使E点传递的力全部传递给H点，如果不在同一水平线上，就会有分力。

3.8 杠杆系应有足够的刚度

因为该结构复杂而紧凑，旋转销的行程比较小（受空间限制）。若杠杆系刚度不足，其受力时会发生较大的弹性变形，就会消耗一部分旋转销的行程。所以拉臂、增力臂、增力推杆均应有足够的刚度。

4 台架试验和整车驻坡试验对上述设计计算的验证

该款车制动器的开发过程，也验证了上述计算分析的正确性。开发经历了两个阶段，台架试验和整车试验结果具有对应性。

4.1 阶段一：刚开发时未充分考虑到各设计要点，结果如下：

（1）制动器台架试验效能因数低，只能达到领从蹄结构的水平。详见表1。

（2）整车坡道驻车试验，满载无法驻18%的坡道。

表1 阶段一的制动器台架试验实测力矩及效能因数

4.2 阶段二：考虑设计要点中的所有要素，对结构进行设计优化，优化后结果如下：

（1）制动器台架试验效能因数达到了双向自增力结构的效能因数。

（2）整车坡道驻车试验，满载可以驻30%的坡道。

表2 阶段二的制动器台架试验实测力矩及效能因数

5 总结

综上所述，本文通过一则实例，分析了一种行车和驻车变结构形式的鼓式制动器，明确给出其力矩计算方法和设计要点，最后通过台架试验和整车驻坡试验进行验证。验证结果表明计算方法正确，设计要点考虑充分。当后轮制动器采用领从蹄鼓式制动器时，如果想在不增大制动器半径的前提下提高驻车制动效能，可以考虑使用这种结构。

[1] 刘惟信,汽车设计 [M] 北京: 清华大学出版社 2001,693-698.

[2] L.鲁道夫,汽车制动系统的分析与设计 [M] 张蔚林、陈名智 译机械工业出版社 1985,18-34.

[3] 方泳龙,汽车制动理论与设计 [M] 国防工业出版社 2005,58-65.

The design and calculation of a kind of drum brake whose structure is different when service brake and parking brake

Cui Xiangbo, Li Bin
( Chery automobile co., LTD Chassis technology research institute Anhui Wuhu 241006 )

The feature of leading-trailing shoe brake is high stability efficiency factor but low efficiency factor; the feature of bi-directional servo brake is low stability efficiency factor but high stability efficiency factor. If we can design a kind of brake, which is leading-trailing shoe brake when service brake, use of the advantage of its high stability efficiency factor;and which is bi-directional servo brake when parking brake, use of the advantage of its high efficiency factor. It will be a kind of brake with great application value. Through an example, the paper give the method of efficiency factor calculation and the key points of design of this kind of brake.

leading-trailing shoe brake; bi-directional servo brake; Variable structure brake; service brake;parking brake

CLC NO.: U463.51+1 Document Code: A Article ID: 1671-7988 (2017)12-09-05

U463.51+1 文献标识码：A 文章编号：1671-7988 (2017)12-09-05

10.16638/j.cnki.1671-7988.2017.12.004

崔祥波（1977-），男，工程师，就职于奇瑞汽车股份有限公司/汽车工程研发总院/底盘技术研究院。从事汽车制动系统的产品设计工作。