基于ADAMS的某重型卡车驾驶室悬置振动模态分析

单长洲，王火文，陈超

（1.安徽江淮汽车集团股份有限公司技术中心，安徽 合肥 230601；2.中国北方车辆研究所，北京 100072）

基于ADAMS的某重型卡车驾驶室悬置振动模态分析

单长洲1，王火文1，陈超2

（1.安徽江淮汽车集团股份有限公司技术中心，安徽 合肥 230601；2.中国北方车辆研究所，北京 100072）

针对一款重卡的驾驶室悬置系统，测量相关参数并通过ADAMS建立驾驶室悬置系统的多体动力学模型，对驾驶室悬置系统的模态和解耦率进行分析和评价，为悬置系统的隔振率优化提供理论基础和改进方向。

驾驶室悬置；ADAMS；模态分析；解耦率；能量法

1 简介

随着重型卡车制造和设计技术的不断发展以及驾驶员对乘坐舒适性要求的提高，作为影响整车平顺性的重要一环，驾驶室悬置系统的减振性能受到越来越多主机厂以及用户的关注。对重卡驾驶室悬置系统的研究往往更关注其系统的隔振率以及平顺性，由于悬置系统结构复杂，随着多体动力学模型的发展，通过建立虚拟样机模型来分析汽车的振动特性已经成为了一个有效的手段[1]。目前对某个方向振动的振型及解耦方面的分析较少，本文将选取一款结构较为简单的驾驶室悬置系统，通过建立ADAMS模型对其振动情况进行分析，为日后进行更为复杂的悬置系统的振动分析进行探索。

2 驾驶室悬置系统结构分析

本文选用某重卡驾驶室悬置系统，其主要结构及三维模型如下图1所示：

该悬置系统较为简单，前悬由左右两侧的橡胶衬套构成，后悬左右两侧分别由一对橡胶衬套与液压锁销轴组成的小总成构成。该悬置具有承载能力强的特点，但是由于选用橡胶作为弹性元件，其行程较小，减振性相较由螺旋弹簧或者空气弹簧作为弹性元件的悬置系统要差。但由于该悬置系统结构相对简单，现选取作为驾驶室振型和解耦分析的对象。

由于驾驶室总成具有六个自由度，分别是沿着X、Y、Z轴的平动和绕着 X、Y、Z轴的转动，要对其六个自由的进行振动分析和解耦分析，必须根据驾驶的质量参数以及减振原件的弹性参数建立动力学模型。

3 驾驶室悬置的参数获得

为了建立更加准确的驾驶室动力学模型，必须对驾驶室的各项参数进行测量，其中主要是驾驶的重量、惯性参数以及减振元件的弹性参数。

3.1 驾驶室重量、惯性参数

由于该款重驾驶室内饰较为简单，对驾驶室惯性参数影响不大，因此采用三维设计软件对于驾驶室的惯性参数进行计算，计算结果如表1。

表1 某重卡驾驶室质量及转动惯量

驾驶室质心同样能够在三维软件中获得，如图2。

图2 某重卡驾驶室模型

3.2 橡胶件弹性参数的测量

利用刚度测量仪，对于前后悬橡胶衬套分别做了径向和轴向的刚度测量，如图3。测得橡胶衬套刚度曲线分别如图4、5、6。

图3 刚度测试台架

图4 前悬橡胶Z向刚度曲线

图5 前悬橡胶Y向刚度

图6 后悬橡胶Z向刚度

通过对橡胶刚度曲线的拟合，得出橡胶各方向刚度值如表2。

表2 驾驶室悬置橡胶衬套刚度值

4 振动模态和解耦率的分析

4.1 悬置结构的ADAMS建模

根据驾驶室悬置系统的特点，按照多体动力学原理，视驾驶室主要部件为刚体。实车中存在大量的连接衬套，对主要橡胶衬套刚度进行线性处理，建模需要考虑橡胶衬套的主要受力方向和转动影响。将驾驶室、悬置主要元件等视为刚体，将驾驶室的质量、质心位置、转动惯量等输入模型中，根据力学参数在模型中添加弹簧和阻尼元件，最后根据驾驶室悬置系统各元件之间的连接方式建立模型的连接副。根据计算获得的驾驶室质量参数以及由实验获得的橡胶元件的刚度，在多体动力学软件ADAMS中建立驾驶室的振动模型。由于本文仅考虑驾驶室的振动，故可将车架与大地固联以简化模型，并且减少整个模型的自由度。

（1）根据原车三维模型测量驾驶室悬置各连接点坐标，在Adams中建立相应的的硬点。

（2）建立驾驶室part，并将part质心坐标定义为之前计算所获得的驾驶室质心坐标，对驾驶室part赋予相应的惯性参数。

（3）由于橡胶衬套具有多个方向上的刚度且在本模型中每个方向上的刚度均不可忽略，故在多体动力学模型中将采用具有多个方向刚度Bushing模拟橡胶连接。在各个橡胶连接点处正确定义驾驶室与车架连接的Bushing并根据实验测得前后橡胶衬套各个方向上刚度对齐进行定义。

通过上述三个步骤，与实车状态一致的驾驶室六自由度动力学模型已经建立完成，可对其进行振动分析，图7。

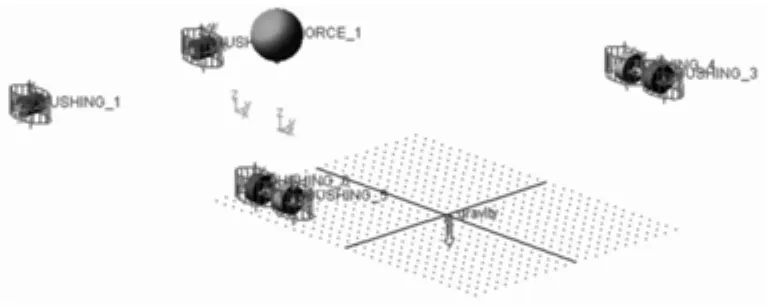
图7 某重卡驾驶室悬置系统多体动力学模型

4.2 振动模态分析，解耦率计算

由于驾驶室悬置系统是一个六自由度振动系统，且六个方向上的运动并非彼此孤立而是存在一定的耦合，即某个方向上的运动必然引起其他方向的运动。耦合的存在将导致驾驶室的振幅加大，振动频率的范围过宽，使得驾驶室的平顺性恶化。故在实际悬置设计中需要尽量对振动的各个方向进行解耦，并且使系统的各阶模态尽量分散以避免引起共振。在众多的解耦方法中能量法应用的最为普遍，所谓能量法就是从能量角度实现各自由度的解耦，从而使系统具有较高的解耦率[2]x

利用拉格朗日方程和虚功原理到系统在广义坐标系下的六自由度振动微分方程：

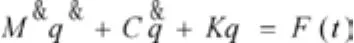
式中M为悬置系统的质量矩阵，C为阻尼矩阵，K为刚度矩阵，q为六个广义坐标列向量，F(t)为系统所受的激励力向量。由于本文中不考虑阻尼和外力作用，因此悬置系统的无阻尼自由振动方程为：

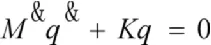
由上式可以计算得到悬置系统的6阶固有频率ωj和固有振型φj，其中j=1,2,3,4,5,6。根据上述的质量矩阵M和振型φj可以得到系统各阶主振动时的能量分布，把它的矩阵形式称为能量分布矩阵。当悬置系统以第j阶模态振动时，其能量分布矩阵可以表示为：

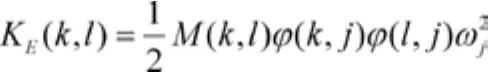
式中k,l,j=1,2,3,4,5,6;M(k,l)为驾驶室质量矩阵的第k行、第l列元素；ωj为悬置系统的第j阶固有频率；φ(k,l)、φ(l,j)分别为系统第j阶振型的第k个和第l个元素。则悬置系统的第j阶振型的第k个坐标的能量与总能量的百分比值为[3]：

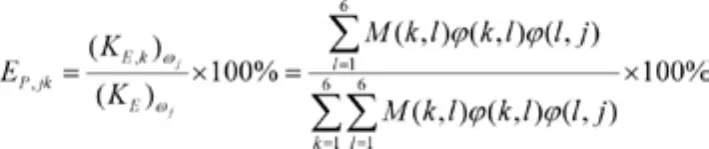
当EP,jk=100%时，系统第j阶模态振动时能量全部集中在第k个广义坐标上，此时该阶模态完全解耦。

模态分析是室悬置系统振动分析中的一个重要手段[4]。进行模态分析，可以了解悬置系统模态分布。通过改进模态分布可以避免驾驶室于汽车其他总成产生共振，有效减少驾驶室内的振动[5]。悬置系统获得良好隔振性能的主要方法是最大限度得解除其多自由度振动耦合[6]。上述建立的六自由度驾驶室悬置系统动力学模型，利用ADAMS软件中的的振动模块，对驾驶室进行模态分析，可以得到驾驶室的模态及相应振型，并可以计算出模态的固有频率以及各模态的特征值。通过分析获得了驾驶室悬置系统的前六阶模态，并且根据能量法分别计算出了每阶振型下各个振动方向上的解耦率，图下表3。

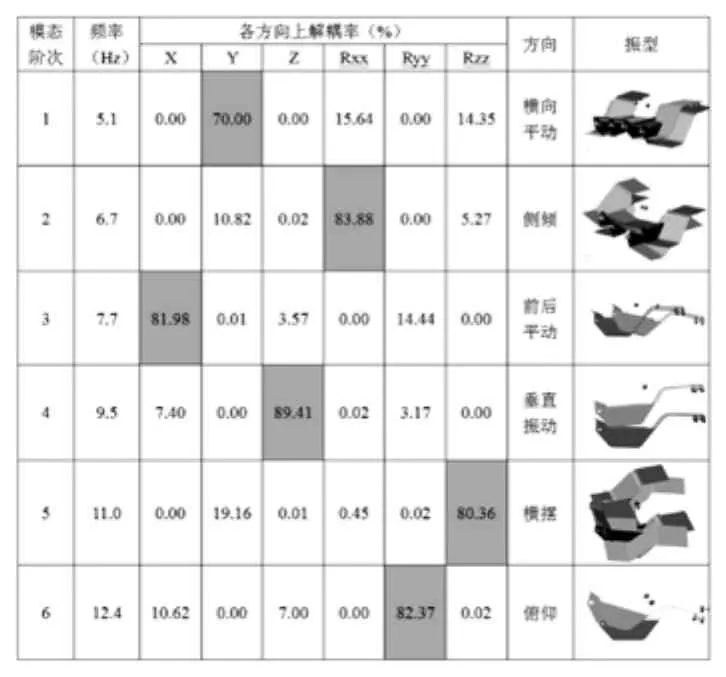
表3 各阶振型及解耦率

由仿真结果得知，该车型驾驶室悬置各阶模态频率分布较为分散（各阶模态频率差均>1Hz），且各个方向上解耦率均较高（除一阶模态外，其余模态解耦率均>80%）。该车型发动机怠速转速600r/min，其怠速激振频率约为25HZ，为了获得良好的怠速减振效果，一般要求驾驶室悬置系统固有频率低于发动机怠速激振频率，各阶频率间隔大于1HZ。分析可知该车型驾驶室悬置系统固有频率范围在5.1HZ~12.4HZ，最高阶频率低于 25HZ，同时各阶频率间隔大于 1HZ，则该系统可获得较好的怠速减振效果。

5 结论

1）通过对驾驶室质量参数及减振元件弹性参数的测量，在ADAMS软件中建立多体动力学模型，能够对于驾驶室悬置系统进行振型及解耦率的分析，对于后续悬置系统的优化能起到一定的指导作用；

2）本文中对于弹性元件参数进行了简化，只考虑了橡胶的刚度特性，并且将其简化为线性刚度；

3）该驾驶室悬置系统各个方向上的解耦率较高，最高阶频率低于发动机的怠速激振频率，同时各阶频率间隔大于1HZ，该系统可获得较好的怠速减振效果；

4）对于较为复杂的全浮式驾驶室悬置系统，也可以采用本文的方法进行振动和解耦率的分析，从而对悬置系统减振性能的进一步提升提供理论依据。

[1] 包继华,张建武,于岩.汽车整车多体系统动力学建模和仿真[J],计算机仿真,2004,21[I]:53-56.

[2] 胡倩,陈剑,沈忠亮等.计及隔振率的发动机悬置系统文件优化设计[J],噪声与振动控制,2015.35（4）78-84.

[3] 徐石安.汽车发动机弹性支撑隔振的解耦方法[J],汽车工程,1995.17（4）198-204.

[4] 刘芳文.某重型卡车驾驶室悬置匹配分析[D],长春:吉林大学汽车工程学院,2004.

[5] 王楷炎,史文库,杨昌海,姚为民.基于 ADAMS的商用车驾驶室悬置系统的振动模态和传递特性.2010.3.

[6] 吕振华,范让林.动力总成—悬置系统振动解耦设计方法.[J]机械工程学报,2005.

Cab mounts Vibration modes Analysis of a heavy truck Based on ADAMS

Shan Changzhou1, Wang Huowei1, Chen Chao2
（1.Jianghuai Automobile Group co., LTD. Technology center, Anhui Hefei 230601; 2.North China Vehicle research institute, Beijing 100072）

Cab mounts system for a heavy truck, measuring related parameters and the cab mounts system was established through ADAMS multi-body dynamics model, the modal of cab mounts system and decoupling rate analysis and evaluation of vibration isolation rate for the suspension system optimization to provide theoretical foundation and the improvement direction.

Cab mounts; ADAMS; Modal analysis; Decoupling rate; Energy method

CLC NO.: U467 Document Code: A Article ID: 1671-7988 (2017)12-233-04

U467 文献标识码：A 文章编号：1671-7988 (2017)12-233-04

10.16638/j.cnki.1671-7988.2017.12.077

单长洲，就职于安徽江淮汽车集团股份有限公司技术中心。