基于PReLUs-Softplus非线性激励函数的卷积神经网络*
郜丽鹏,郑 辉
(哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001)
基于PReLUs-Softplus非线性激励函数的卷积神经网络*
郜丽鹏,郑 辉
(哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001)
针对卷积神经网络表达能力和识别效果受卷积层激励函数影响的问题,提出了一种新型非线性激励函数PReLUs-Softplus,并将其应用于神经网络卷积层.对新型神经网络和采用传统激励函数的神经网络在MNIST和CIFAR-10标准数据库上进行了图像识别对比实验,结果表明,相比于采用传统激励函数的神经网络,使用PReLUs-Softplus激励函数的卷积神经网络在不同的池化方式下图像识别计算收敛速度更快,显著降低了识别的错误率.
深度学习;卷积神经网络;激励函数;模式识别;非线性映射;池化;网络结构;图像识别
与传统的神经网络不同,卷积神经网络作为深度学习中一种常见的模型,输入是原始图像,而非提取出来的图像特征,免去了复杂的特征提取过程.卷积神经网络模型作为新兴的分类器在多个领域得到了广泛应用,如字符识别[1]、语音识别[2]、人脸识别[3]、人体行为理解[4]、交通信号识别[5]、情感识别[6]和手势识别[7-8]等.在卷积神经网络结构中,卷积的操作过程是线性的,表达能力较弱.通过使用非线性映射的激励函数可以显著提高神经网络的表达能力,激励函数的选取直接决定着网络性能的优劣.饱和非线性激励函数如双曲正切函数(Tanh)和S形生长曲线(Sigmoid)在神经网络领域取得了良好成果,但存在收敛速度慢和梯度弥散导致的不收敛等问题.近年来,生物学家建立了能够更加精确地模拟脑神经元接受信号过程的激励模型ReLUs(Rectified Linear Units).ReLUs模型具有计算简单、收敛速度快和识别精度高等优点,较好地解决了使用Tanh函数和Sigmoid函数的神经网络存在的问题,但是ReLUs函数网络可能导致神经元坏死的现象[9].随后有学者提出了ReLUs函数的变形函数形式ReLUs-Leaky和PReLUs(Parametric ReLUs),这两种函数继承了ReLUs函数的优点,具备一定的稀疏能力,解决了神经元坏死的问题.但是以上三种ReLUs族激励函数在x轴的正半轴没有本质变化,对神经网络进行了线性修正,因此欠缺对模型的表达能力.Softplus函数是对ReLUs函数的一种非线性表达,Softplus函数是一个近似光滑的非线性函数,从曲线形式上看更加契合生物神经元的激活特征,但欠缺稀疏表达能力.本文综合PReLUs和Softplus函数优点,提出了一种新的不饱和非线性函数PReLUs-Softplus,其具备稀疏表达能力,收敛速率快,识别精度高.
1 卷积神经网络
卷积神经网络有别于其他形式的神经网络,通过对输入的原始图像进行直接卷积运算实现对旋转、平移和放缩图像的自适应识别,其网络结构如图1所示.
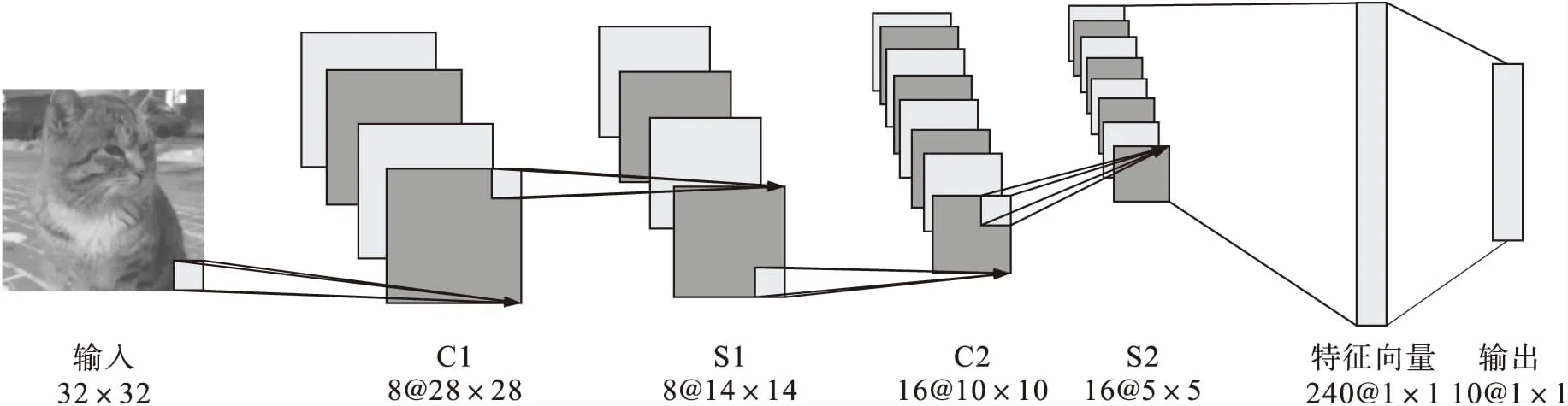
图1 卷积神经网络结构Fig.1 Convolutional neural network structure
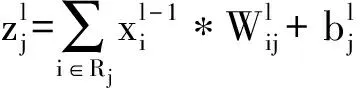
(1)
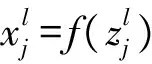
(2)
式中,f(·)为神经元的激励函数.
采样层是通过降采样和池化手段获得特征图像的子模块集合,子模块之间不能互相重叠.CNNs采样层的池化方式分为均值池化、最大池化和随机池化三种形式[10].
卷积神经网络与其他神经网络的相同之处是均采用前向传播学习进行图像分类,采用反向传播更新权重和偏置的方式进行学习.不同之处在于卷积神经网络的权值和偏置以卷积核的形式存在,前向传播通过多层卷积层和采样层的交替作用直接学习原始图像[11].反向传播算法更新权值的公式为
W(t+1)=W(t)-ηδ(t)x(t)
(3)
式中:x(t)为该神经元的响应输出;δ(t)为该神经元的误差项;η为学习率.
CNNs的输入层和采样层均不含激活函数,通常使用CNNs模型进行分类时,输出层一般采用Sigmoid函数.因此,本文仅对卷积层使用不同激活函数的神经网络模型的性能进行研究.
2 常用激活函数及其特性
卷积神经网络提出后,激励函数的选择一直是学者们研究的热点.Tanh、Sigmoid激励函数和Softplus、ReLUs激励函数以及ReLUs族函数的图形如图2~4所示,其表达式分别如下所示.
1) 饱和非线性函数
Tanh函数的表达式为
图1给出了从故障开始到重合闸的设备操作顺序,如保护继电器、断路器、重合闸继电器等。在继电保护动作和断路器跳闸后,断路器重合闸之前还需要电去离子时间。在此期间,次级电弧应灭弧。根据断路器的断开与断路器重合闸以恢复电力传输之间的间隔定义重合闸间歇时间:

图2 饱和非线性函数曲线Fig.2 Saturated nonlinear function curves
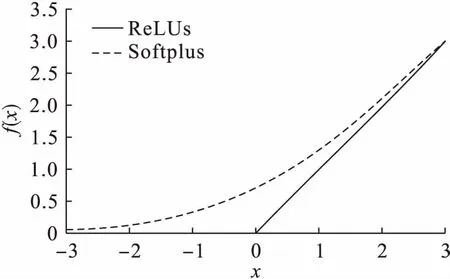
图3 不饱和非线性函数曲线Fig.3 Non-saturated nonlinear function curves
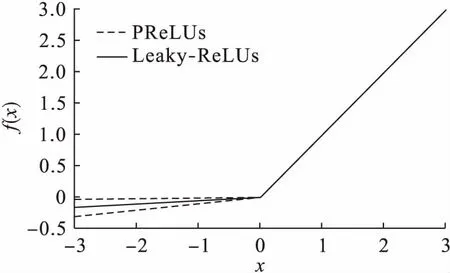
图4 ReLUs族函数曲线Fig.4 ReLUs family function curves f(x)=(ex-e-x)/(ex+e-x)
(4)
Sigmoid函数的表达式为
f(x)=(1+e-x)-1
(5)
2) 不饱和非线性函数
ReLUs函数的表达式为
f(x)=max(0,x)
(6)
Softplus函数的表达式为
f(x)=ln(ex+1)
(7)
3) ReLUs族函数
ReLUs族函数的表达式为
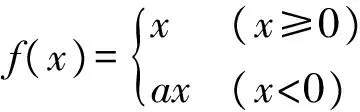
(8)
由图2可知,饱和非线性激励函数Tanh的曲线与Sigmoid函数的曲线具有相同的趋势,只是函数值域不同.由于激励函数的输出中心为零,不会出现权重“Z”字下降情况,但是激励函数关于零点奇对称的特性与生物神经元的基本特征并不相符.Sigmoid函数具有连续可微分性的特征,一度成为激活函数的最优选择,但是后续研究表明其不具有稀疏特性,而且收敛速度较慢.由图3可知,ReLUs激励函数曲线自变量小于0时的输出为0,从而获得稀疏表达能力;Softplus函数是对ReLUs函数的非线性平滑表示,具有非线性映射纠正的能力,但其欠缺稀疏表达能力.在ReLUs族函数的Leaky-ReLUs函数表达式中,a通常取一个较小的数,如0.01、0.05等固定值,不再是直接压缩至0,而是将x<0部分的输出值压缩1/a倍,这样既起到修正数据分布的稀疏作用,又不会造成神经元坏死,在后面几层需要负轴信息时不至于完全无法恢复.PReLUs表达式中的a是在高斯分布中抽取的一个随机数,在测试过程中可对a进行修正.研究人员通过实验论证指出,相比Leaky-ReLUs函数,PReLUs函数的图像识别准确率提高了1.03%.PReLUs函数继承了Leaky-ReLUs函数的一切优点,但是由于ReLUs族激励函数对x>0部分的数据只进行了线性修正,所以对样本模型的表达能力仍有所欠缺.
3 PReLUs-Softplus激活函数及其特征
综合PReLUs和Softplus等非线性修正激活函数的特点,本文提出了一种新型非线性饱和激励函数.该激励函数继承了PReLUs激活函数的稀疏特性和Softplus函数的光滑特性,既实现了稀疏表达,又不会造成神经元坏死,同时还实现了激励函数的光滑非线性映射,更贴近于人脑神经元的激励模型.分别对Softplus函数和PReLUs函数进行变换,就可得到PReLUs-Softplus激励函数,即首先将Softplus函数曲线下移ln 2个基本单位,然后把x<0部分的输出数据设为ax,修正后函数记为PReLUs-Softplus,函数曲线如图5所示,其表达式为
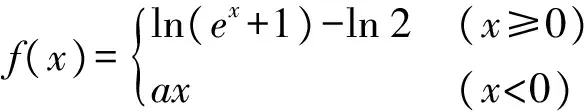
(9)
由图5可以看出,a为一个被训练的常数,PReLUs-Softplus激励函数的负半轴斜率将根据实时训练发生变化,最终收敛为适宜的常数.PReLUs-Softplus具有灵活的稀疏表达能力,为了增强对样本模型的表达能力,该激励函数对x>0部分的数据进行了连续光滑的非线性修正,此外该激活函数一阶导数曲线在x>0的部分是连续光滑的增函数,在卷积层应用该激励函数的神经网络更容易收敛并获得最优解.

图5 PReLUs-Softplus函数曲线Fig.5 PReLUs-Softplus function curves
4 实验结果及分析
为了验证采用PReLUs-Softplus激励函数卷积神经网络在图像识别中应用的效果,分别在MNIST和CIFAR-10数据库上进行了实验研究.全输出层的激励函数均为Sigmoid函数,卷积层的激励函数分别选取本文提出的PReLUs-Softplus和传统的激励函数,对比两种网络的识别效果.实验设置如下:Matlab版本为2016a,操作系统为Windows 7专业版,CPU为INTEL i7-6700,主频为3.4 GHz,内存为8 GB.
4.1 MNIST实验
MNIST库为手写罗马数字(0~9)数据库,其中包含训练图片60 000张,测试图片10 000张,图片规格为28×28大小的灰度图像.样本库中部分训练图片如图6所示,部分测试图片如图7所示.

图6 部分训练图片Fig.6 Partial training images
CNNs网络结构设置为6C-2S-12C-2S-200F,卷积核大小为5×5,6C/12C表示映射出6个卷积层/12个卷积层;2S表示采样窗口为2的采样层;200F表示200个神经元组成的全连接层.CNNs网络模型的训练过程中,由于实验环境和网络结构以及选择激励函数的不同,训练时间也会存在差别,本文实验中进行一次训练的时间约为40~70 s.以Softplus激励函数神经网络为例,遍历整个训练库,每训练50张图片迭代一次,最终获得卷积层和全连接层的权值和偏置,第二层神经层(卷积层)和第四层神经层的权值如表1、2所示,限于篇幅,表3只列举了全连接层的偏置.错误率收敛如图8所示,可见使用PReLUs-Softplus激励函数的卷积神经网络在迭代400次后错误率就下降到0.1%以下,相较于常用的Sigmoid激励函数收敛速度显著加快.
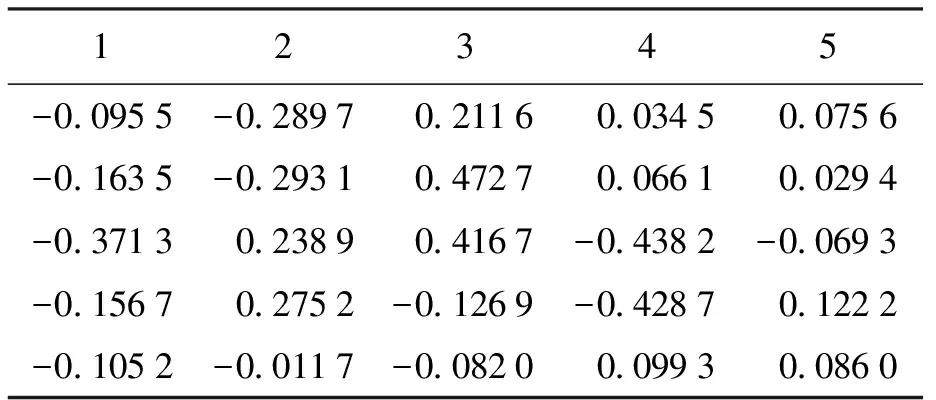
表2 神经网络第四层训练所得权值Tab.2 Training weight in fourth layer of neural network
采样层的池化方式均采用均值池化,卷积层分别使用Sigmoid、Tanh、ReLUs、Softplus、Leaky-ReLUs、PReLUs-Softplus函数作为激励函数.采用不同激励函数神经网络的分类正确率随迭代次数变化的曲线如图9所示.

表3 神经网络连接层偏置Tab.3 Offset of connected layer in neural network
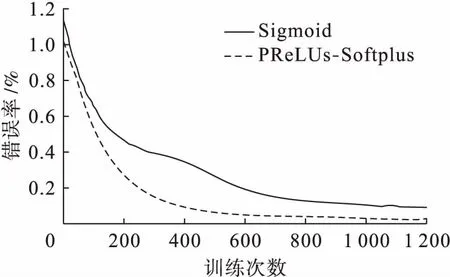
图8 错误率收敛Fig.8 Convergence of error rate
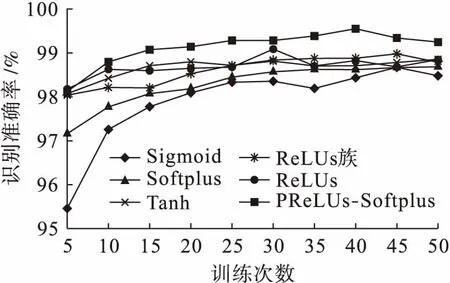
图9 不同激励函数下的网络识别准确率Fig.9 Network recognition accuracy under different excitation functions
正确率的计算公式为
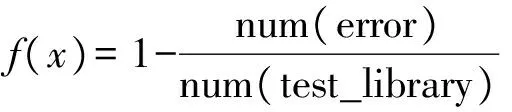
(10)
式中:num(error)为分类错误的图片数;num(test_library)为测试图片总数.
从图9中可以看出,以MNIST数据集作为实验对象,卷积层使用Sigmoid函数作为激励函数的网络结构收敛速度最慢,最高识别率只有98.5%;使用Tanh激励函数的神经网络取得了较好的收敛效果和识别准确率,其准确率达到98.87%;使用Softplus函数作为卷积层激励函数的网络收敛速度相比于Sigmoid函数有所提高,识别准确率提高至98.80%;使用ReLUs函数作为卷积层激励函数的神经网络收敛速度较快,识别准确率达到99.09%;使用ReLUs族函数的收敛速度进一步提升且准确率最高可达到99%以上;使用本文提出的PReLUs-Softplus激活函数的卷积神经网络的识别准确率高达99.55%.
池化方式分别采用最大值池化和随机池化进行上述实验,数据库遍历次数设置为50次,测试结果如表4所示.

表4 MNIST数据集实验结果Tab.4 Experimental results in MNIST database %
从表4中可以看出,在实验的测试训练过程中,采样层的池化方式为最大池化时,传统的激活函数网络错误率均约为1.2%,而使用PReLUs-Softplus激励函数的网络错误率降低至0.72%;采用随机池化时,传统的激活函数网络错误率均约为1.5%,而使用PReLUs-Softplus激励函数的网络错误率仅为0.65%,网络识别性能得到了明显改善.通过上述实验验证可知,PReLUs-Softplus激励函数神经网络在不同池化方式下均能明显地提高图像识别的准确率.
4.2 CIFAR-10数据库实验
CIFAR-10数据库中含有图片60 000张,图片均为32×32的规格,其中50 000张用于神经网络的训练,10 000张用于测试神经网络的性能.CIFAR-10数据库中的图片均为彩色图片,因此在使用CNNs网络时需要先进行灰度处理,然后进行归一化.网络结构的设置为8C-2S-16C-2S-240F,卷积核的大小仍为5×5.采样层选取不同池化方式,卷积层选取不同激励函数,神经网络图像识别的错误率如表5所示.
从表5可以看出,在不同池化方式下,选取PReLUs-Softplus作为激励函数的神经网络识别的错误率最低.
实验结果表明,在选取不同池化方式的条件下,卷积神经网络中使用PReLUs-Softplus作为激励函数,在两种数据集上均取得了较传统神经网络更低的识别错误率.其中,MNIST数据集上的最低错误率达到0.45%,而CIFAR-10数据集上错误率可降低至31.20%,相较其他形式的激励函数识别错误率分别降低了约1%和2%.
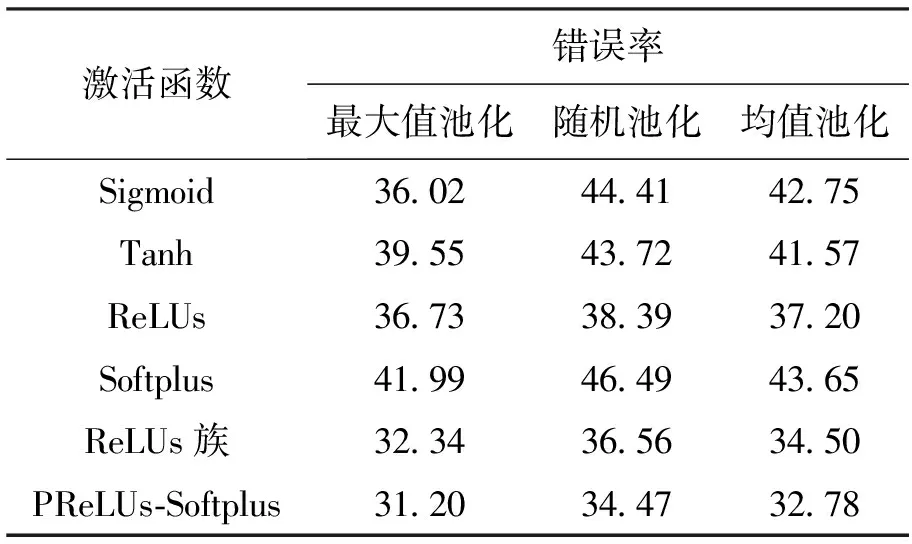
表5 CIFAR-10数据集实验结果Tab.5 Experimental results in CIFAR-10 database %
5 结 论
本文针对深度学习算法中卷积神经网络卷积层ReLUs激励函数对模型表达能力的不足,ReLUs族函数作为激励函数时容易导致神经元坏死,Softplus函数欠缺稀疏表达能力等问题,提出了一种新型非线性修正函数PReLUs-Softplus作为神经元激励函数.在MNIST和CIFAR-10两个数据集上分别进行相关实验,结果表明,在采用多种池化方式的卷积神经网络结构中,使用PReLUs-Softplus非线性修正函数作为激励函数显著提高了图像识别的收敛速度,在MNIST数据集上,识别准确率最高达到99.55%;在CIFAR-10数据集上识别准确率最高达到68.80%,相较于其他传统激励函数,准确率均有所提高.
[1] Krizhevsky A,Sutskever I,Hinton G E.ImageNet classification with deep convolutional neural networks [C]//Advances in Neural Information Processing Systems.New York,USA,2012:1097-1105.
[2] Abdel-llamid O,Mohamed A R,Hui J,et al.Convolutional neural networks for speech recog-nitionl [J].IEEE-ACM Transactions on Audio Speech and Language Processing,2014,22(10):1533-1545.
[3] Cheung B.Convolutional neural networks applied to human face classification [C]//11th International Conference on Machine Learning and Applications.Boca Raton,USA,2012:580-583.
[4] Ji S W,Xu W,Yang M,et al.3D convolutional neural networks for human action recognition [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(1):221-231.
[5] Jin J Q,Fu K,Zhang C S.Traffic sign recognition with hinge loss trained convolutional neural networks [J].IEEE Transactions on Intelligent Tranportation Systems,2014,15(5):1991-2000.
[6] Mao Q R,Dong M,Huang Z W,et al.Learning salient features for Speech emotion recognition using convolutional neural networks [J].IEEE Transaction on Multimedia,2014,16(1):2203-2213.
[7] Stefan D,Berlemont S,Lefebvre G,et al.3D gesture classification with convolutional neural networks [C]//IEEE International Conference on Acoustics.Florence,Italy,2015:5432-5436.
[8] Li S Z,Yu B,Wu W,et al.Feature learning based on SAEPCA network for human gesture recognition in RGBD images [J].Neuron Computing,2015,15(2):565-573.
[9] Nair V,Hinton G E.Rectified linear units improve restricted boltzmann machines [C]//Proceeding of the 27th International Conference on Machine Lea-rning(ICML-10).Madison,USA,2010:807-814.
[10]Zeiler M D,Fergus R.Stochastic pooling for regularization of deep convolutional neural networks [C]//International Conference on Learning Representation.Scottsdale,USA,2013:1-9.
[11]牛连强,陈向震,张胜男,等.深度连续卷积神经网络模型构建与性能分析 [J].沈阳工业大学学报,2016,38(6):662-666.
(NIU Lian-qiang,CHEN Xiang-zhen,ZHANG Sheng-nan,et al.Model construction and performance analysis for deep consecutive convolutional neural network [J].Journal of Shenyang University of Technology,2016,38(6):662-666.)
ConvolutionalneuralnetworkbasedonPReLUs-Softplusnonlinearexcitationfunction
GAO Li-peng, ZHENG Hui
(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)
Aiming at the problem that the expression ability and recognition effect of convolutional neural network (CNN) are affected by the excitation function of convolutional layer, a new nonlinear excitation function PReLUs-Softplus was proposed and applied to the convolutional layer in neural network.The contrast experiments on the image recognition of both new neural network and neural network with the traditional excitation function were performed in MNIST and CIFAR-10 standard database.The results show that compared with the neural network with the traditional excitation function, the convolutional neural network with PReLUs-Softplus excitation function has faster convergence rate in the calculation of image recognition under different pooling methods, and can effectively reduce the recognition error rate.
deep learning; convolutional neural network; excitation function; pattern recognition; nonlinear mapping; pooling; network structure; image recognition
2016-11-02.
国家自然科学基金资助项目(61571146).
郜丽鹏(1972-),男,黑龙江哈尔滨人,教授,博士,主要从事宽带信号检测、处理和识别以及信息融合等方面的研究.
* 本文已于2017-10-25 21∶12在中国知网优先数字出版.网络出版地址:http://kns.cnki.net/kcms/detail/21.1189.T.20171025.2112.020.html
10.7688/j.issn.1000-1646.2018.01.10
TN 953
A
1000-1646(2018)01-0054-06
钟 媛 英文审校:尹淑英)

