H型精密运动平台交叉耦合模糊PID同步控制*
王丽梅,张宗雪
(沈阳工业大学 电气工程学院,沈阳 110870)
电气工程
H型精密运动平台交叉耦合模糊PID同步控制*
王丽梅,张宗雪
(沈阳工业大学 电气工程学院,沈阳 110870)
针对双直线电机驱动的H型精密运动平台由于永磁直线同步电机参数变化和扰动等不确定因素致使两边的运动不同步问题,提出一种交叉耦合模糊PID控制方法.在单轴中采用模糊PID控制作为位置控制器,速度控制器用普通的PI控制,以保证单轴跟踪精度;双轴间引入交叉耦合控制方法,消除双电机之间存在的机械耦合,进而减小了双轴间的位置同步误差.结果表明,将交叉耦合与模糊PID相结合的控制方法能够使H型精密运动平台的同步误差收敛于零,并且使系统具有较好的跟踪性能与鲁棒性.
H型精密运动平台;交叉耦合控制;模糊PID控制;同步误差;永磁直线同步电机;跟踪精度;同步运动;机械耦合
H型精密运动平台是一种特殊的笛卡尔结构,在促进微电子的自动化流程、精密测量、电路组件、印刷电路板制造及平板制造和检测中得到了广泛的应用[1-3].H型精密运动平台采用的是将两个电机安装在两平行直线导轨上的结构,采用永磁直线同步电机以获得高速高精度的运动.由于采用了双边驱动的方式,H型精密运动平台可以获得高功率密度,尽管对两边采用相同的电机结构和控制方法,但也会由于电机参数变化、摩擦力的不平衡和负载变动等不确定因素导致两边的运动无法达到完全一致,影响加工工件的质量,甚至产生过电流保护而造成工作过程的卡顿.因此,在保证单轴的精密运动控制外,对H型精密运动平台的同步误差控制成为了当下的研究热点.
国内外很多学者对此进行了深入的研究,其中新加坡学者为H型精密运动平台建立了基于拉格朗日方程的动力学模型,并设计自适应控制算法,极大地减小了单轴的跟踪误差,但并没有减小双轴间的同步误差[4-5];文献[6-7]基于频域进行控制器优化,但双边同步控制并没有考虑质心偏移对控制性能的影响;台湾的林法政提出了基于DSP的交叉耦合RBF(radial basis function,径向基函数)网络控制,并建立了包括参数变化、外部扰动和非线性摩擦力在内的总不确定集的单轴运动系统动力学模型[8];在此研究基础上,林法政提出了互补滑模的控制方法,来保证单轴位置跟踪精度的要求,并且采用Sugeno型模糊神经网络作为补偿器的控制算法来消除同步误差,提高了双轴间的同步误差精度[9];北京航空航天大学的刘强为对称的H型结构精密运动平台设计了同步控制器[10],使用基于速度偏差的模糊PID控制方法,实现了双边同步控制,获得较高的同步运动精度.
在数控机床加工和多轴运动控制领域中曾大量采用交叉耦合的控制方法得到较高的轮廓加工精度[11-13].基于差分计算算法的变参数交叉耦合控制弥补了单轴伺服跟踪误差补偿轮廓误差效果不理想的缺点[11].为减小数控机床各联动轴动态性能不一致所导致的较大轮廓误差,文献[12]提出了一种NURBS插补器交叉耦合控制方法.
本文针对双直线电机驱动的H型精密运动平台由于永磁直线同步电机参数变化和扰动等不确定因素致使两边的运动不同步的问题,首先建立了包含永磁直线同步电机参数变化、外部扰动和摩擦力等不确定集的H型精密运动平台的数学模型,然后在此模型基础上提出了交叉耦合模糊PID的控制方法.利用模糊推理控制方法,在线自整定PID三个参数以保证单轴跟踪精度,双轴间采用交叉耦合的控制方法消除两轴间的耦合影响,从而减小位置同步误差,最后通过matlab/simulink仿真验证了所提方法的有效性.
1 H型精密运动平台数学模型
本文使用的H型精密运动平台结构如图1所示,它将两台参数完全相同的永磁直线同步电机(PMLSM)安装在两个平行导轨上以驱动x轴方向的电机沿y轴方向水平移动.采用磁场定向控制方法,简化电磁力Fei为
Fei=Kfiiqi
(1)
Kfi=3πnpiλPMi/(2τ)
(2)
式中:Kfi为电磁推力系数;iqi为q轴电流;λPMi为永磁体磁链;npi为磁极对数;τ为极距,τ=32 mm;i=1,2,分别指H型精密运动平台的Y1轴,Y2轴.

图1 H型精密运动平台结构Fig.1 Structure of H-type precision motion platform
永磁直线同步电机的机械运动方程为

(3)
式中:vi为电机的动子速度;Mi为电机动子质量;Di为粘滞摩擦系数;Fi为扰动,包括电机端部效应、参数变化、系统外界扰动及非线性摩擦力等.
假设不存在扰动Fi,根据式(1)、(3)可得理想状态下永磁直线同步电机的动态方程为
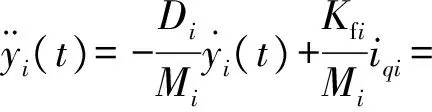
(4)
式中:yi(t)为动子位置;ui为控制器输出,ui=iqi,即q轴电流.考虑各种不确定因素存在时,则式(4)的动态方程变为
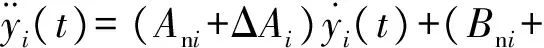
ΔBi)ui+(Cni+ΔCi)Fi=
(5)
式中:Cni=-1/Mi;ΔAi、ΔBi和ΔCi为系统参数Mi和Di所引起的不确定量;Hi为系统不确定量总和,表示为
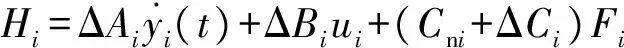
(6)
本文假设Hi有界,即|Hi|≤ρ,ρ为正常数.
2 交叉耦合模糊PID控制器设计
H型精密运动平台的同步控制结构如图2所示,控制器包括位置控制器、速度控制器以及交叉耦合控制器.Y1轴和Y2轴的位置跟踪误差作为交叉耦合控制器的输入,位置控制器采用模糊PID控制,其输入为经过交叉耦合控制器输出的混合误差,速度控制器采用普通PI控制,速度控制器的输出作为H型精密运动平台的输入信号.
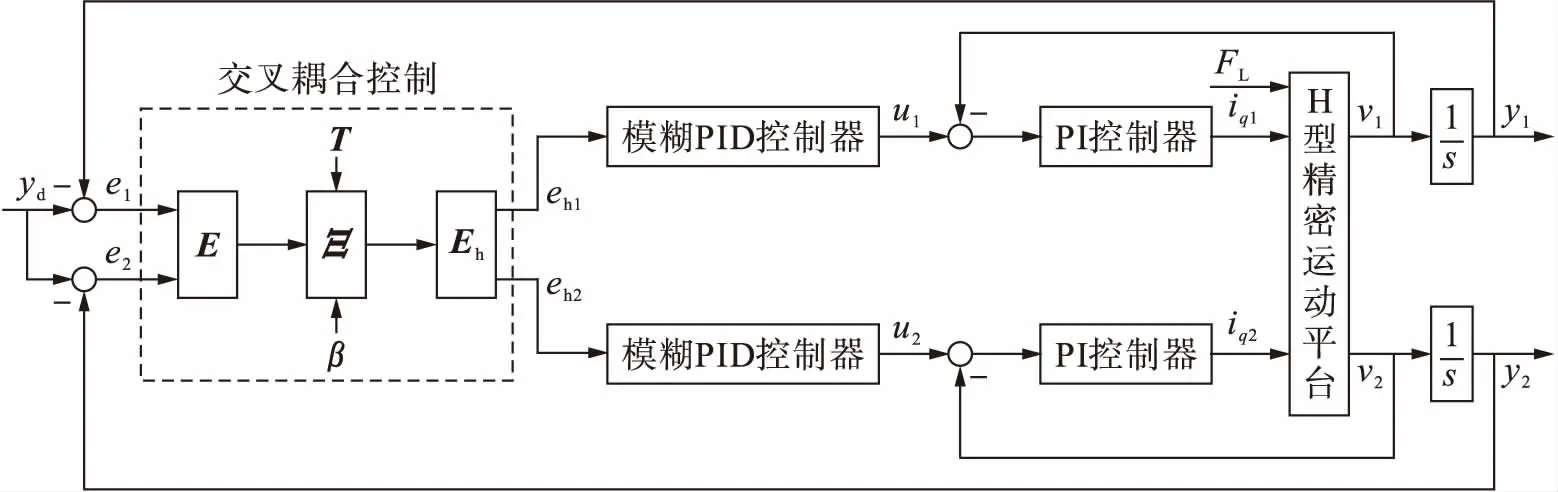
图2 H型精密运动平台控制结构Fig.2 Structure of H-type precision motion platform control
2.1 交叉耦合控制器设计
考虑H型精密运动平台Y1轴和Y2轴的单轴位置跟踪误差及轴间的位置同步误差,首先定义位置跟踪误差为
ei=yd-yi
(7)
式中,yd为期望位置输入.定义同步误差为
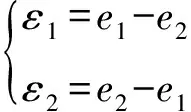
(8)
式中,ε1和ε2分别为Y1轴和Y2轴的同步误差.如果同步误差ε1和ε2等于零,那么H型精密运动平台的两轴即为同步运动,用矩阵形式表示式(8)为
Ξ=TE
(9)
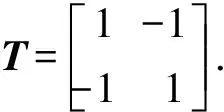
为了同时减小位置跟踪误差和同步误差,将两误差相结合,定义为混合误差,即
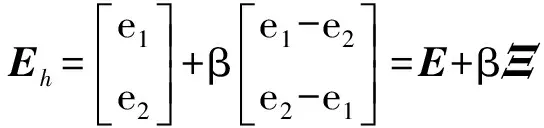
(10)
式中:Eh=[eh1,eh2]T,eh1和eh2分别为Y1轴和Y2轴的混合误差;β为两直线电机的耦合系数.将式(9)带入式(10)得到
Eh=(I+βT)E
(11)
式中,I为单位矩阵,则(I+βT)为正定矩阵.式(11)中,当且仅当E→0,才有Eh→0,即Ξ→0,因此,控制目标就是要设计一个能够同时减小位置跟踪误差和同步误差的控制器.
2.2 模糊PID控制器设计
模糊控制是智能控制的一个重要分支,对不能准确确定控制对象数学模型的系统具有很好的适应性和鲁棒性.本文将模糊控制与传统PID控制相结合,根据不同时刻偏差量及偏差变化量之间的关系,对KP,KI和KD三个参数进行在线修正,以满足对不断变化的控制过程的要求,使H型精密运动平台系统具有较好的性能.模糊PID控制框图如图3所示,经交叉耦合控制器输出的混合误差ehi及其变化率chi为输入语言变量,KP,KI,KD为输出语言变量,调整公式为
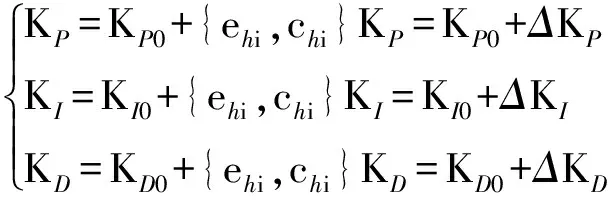
(12)
式中,KP0,KI0和KD0分别为KP,KI和KD的初始参数.将{NB,NM,NS,ZE,PS,PM,PB}设置为输入变量ehi和chi及输出变量KP,KI,KD的模糊子集,选取输入变量ehi和chi的量化论域为[-6,6],隶属函数为高斯函数;输出变量KP,KI和KD的量化论域为[-3,3],隶属函数为三角形函数.
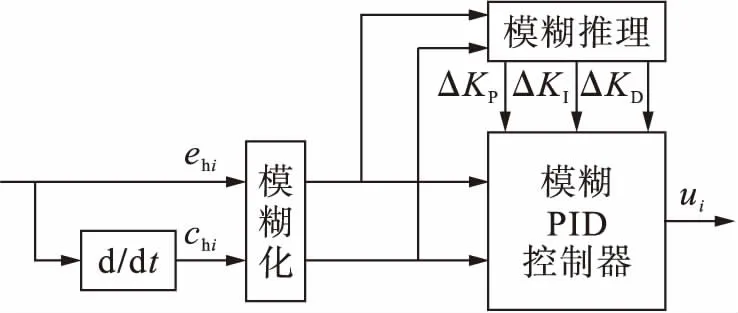
图3 模糊PID控制结构Fig.3 Structure of fuzzy PID control
模糊PID控制器输出控制律ui为
(13)
模糊规则是根据实际经验建立的参数KP,KI和KD在不同ehi和chi下的模糊逻辑表,模糊逻辑规则如表1所示.当混合误差较大时,无论混合误差的变化趋势如何,都应取较大的ΔKP和较小的ΔKD以使系统具有较好的快速性,同时为了避免系统响应超调较大,应取较小的ΔKI来限制积分作用;当混合误差为中等大小时,选取小的ΔKP使系统响应超调较小,同时为保证系统的响应速度,ΔKI和ΔKD大小应适中,其中ΔKD的取值对系统响应的影响较大;当混合误差较小时,为保证系统较好的稳态性能,ΔKP和ΔKI应大些,同时为避免系统在设定值附近发生振荡,并考虑系统的抗干扰性能,当混合误差变化率较小时,ΔKD取值可大些.
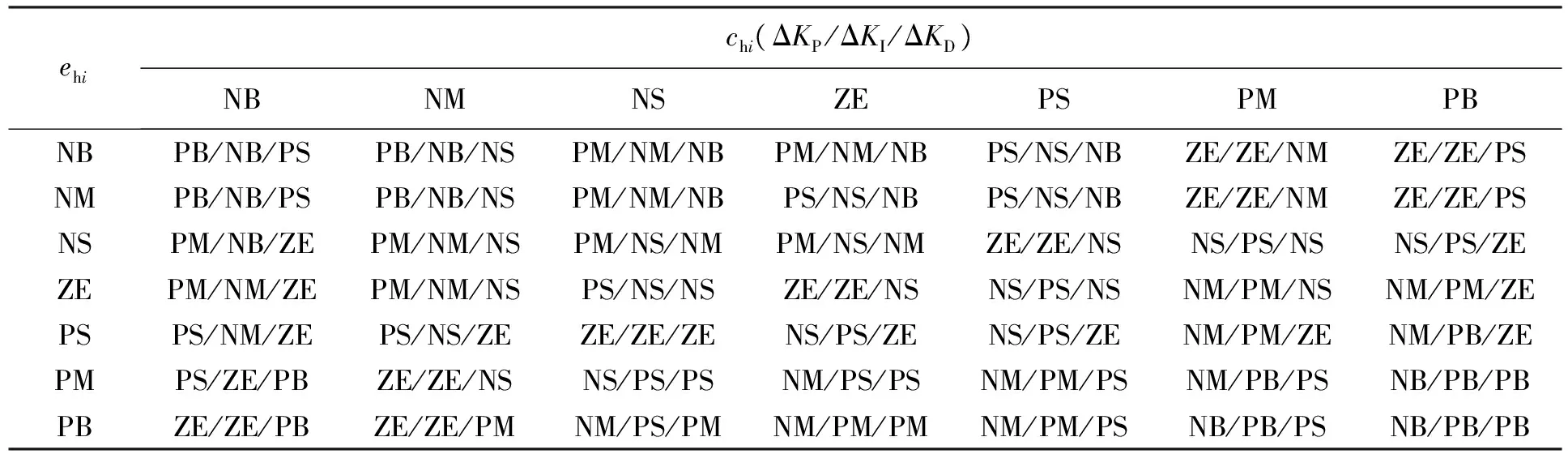
表1 PID控制器模糊逻辑规则Tab.1 Fuzzy logic rule of PID controller
3 仿真结果及分析
为了验证针对H型精密运动平台同步控制问题所提出的交叉耦合模糊PID控制的有效性,对所提出的控制方案进行仿真研究.根据H型平台的结构和电机参数,各部分的参数设置为M1=M2=8.2 kg,Kf1=Kf2=15.75 N/A,D1=D2=6.3 N·s/m,ρ=300,交叉耦合控制器的耦合系数β=0.3,模糊PID控制器KP0=200,KI0=10,KD0=0,速度控制器KPv=250,KIv=10 000.
图4、5为在2 s向各轴突加63 N的额定负载扰动时,H型精密运动平台的单轴期望位置输出和实际位置输出的曲线.由图4、5可以明显看出,在交叉耦合模糊PID控制器的作用下,实际输出曲线和期望输出曲线轨迹基本一致,具有良好的跟踪惯性.
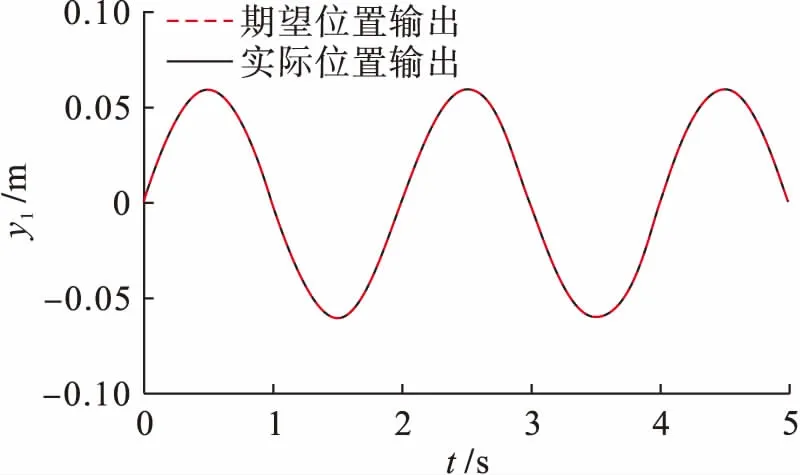
图4 Y1轴位置跟踪曲线Fig.4 Position tracking curve of Y1 axis
图6、7为相同仿真条件下,在普通PID控制、交叉耦合PID控制和交叉耦合模糊PID控制情况下的单轴位置误差响应曲线.由图6、7可知,Y1轴的最大位置误差分别为0.142,0.098和0.064 mm;Y2轴的最大位置误差分别为0.131,0.094和0.061 mm.对比这三种方法可以明显看出,文中所提出的交叉耦合模糊PID控制能提高系统的跟踪精度,这样可以保证H型精密运动平台控制系统具有较好的抗扰性和较强的鲁棒性.
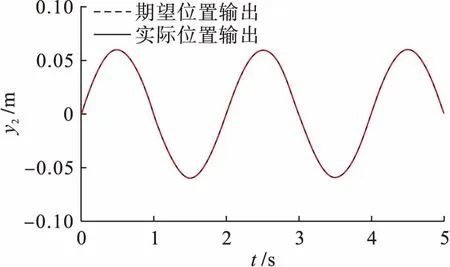
图5 Y2轴位置跟踪曲线Fig.5 Position tracking curve of Y2 axis
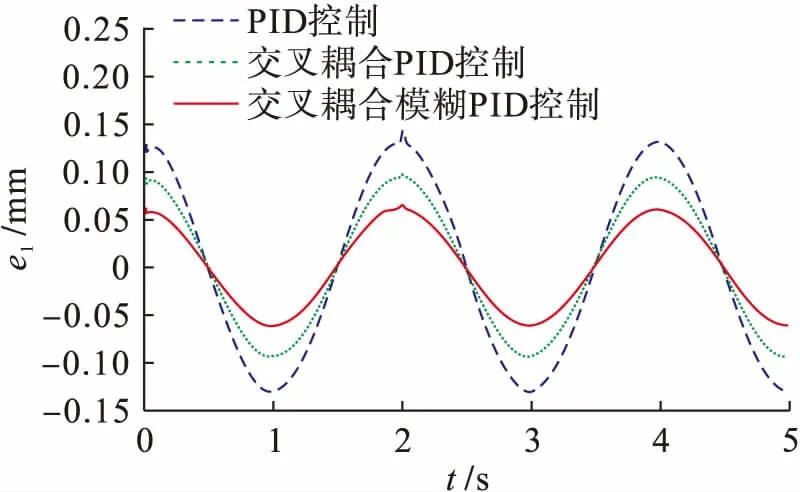
图6 Y1轴位置误差跟踪曲线Fig.6 Position error tracking curve of Y1 axis
图8为在同样仿真条件下,三种不同控制方法输出的位置同步误差响应曲线.由图8可以看出,三种控制方法的同步误差基本可以收敛到零,但是普通PID在受到扰动后的最大同步误差达到了0.169 mm,而加入交叉耦合的PID控制最大同步误差为0.088 mm,本文所提出的交叉耦合模糊PID控制进一步提高了同步误差精度,将最大同步误差减小到0.056 mm.因此,交叉耦合模糊PID控制能够使系统具有更好的抗扰性和鲁棒性.
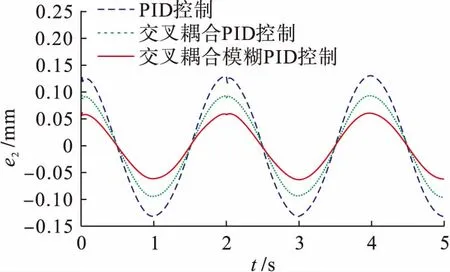
图7 Y2轴位置误差跟踪曲线Fig.7 Position error tracking curve of Y2 axis
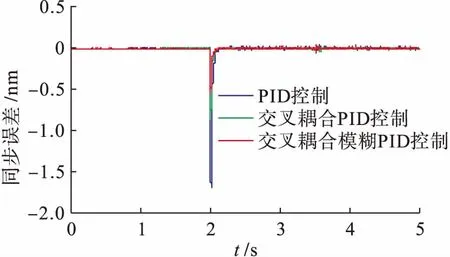
图8 Y1轴与Y2轴位置同步误差曲线Fig.8 Synchronous position error curve between Y1 and Y2 axex
4 结 论
通过分析由永磁直线同步电机参数变化、扰动和摩擦力等不确定性造成的H型精密运动平台的运动不同步问题,本文设计了交叉耦合模糊PID控制器,将模糊推理与PID控制方法相结合以保证单轴控制精度,再利用交叉耦合的方法消除机械耦合对平台的影响,从而实现同步控制.仿真结果表明,交叉耦合模糊PID控制明显减小了单轴的位置跟踪误差,提高了单轴的跟踪精度.双轴间的同步误差可以收敛到零,并且削弱了负载扰动对控制系统的影响,进而提高系统的抗扰性和鲁棒性.
[1] Li C,Yao B,Wang Q.Adaptive robust synchronous motion control of dual parallel linear motor driven stage [C]//ASME 2012 5th Annual Dynamic Systems and Control Conference Joint with the JSME 2012 11th Motion and Vibration Conference.Florida,USA,2012:93-100.
[2] Li P,Zhu G,Gong S,et al.Synchronization control of dual-drive system in gantry-type machine tools based on disturbance observer [C]//2016 12th IEEE/ASME International Conference.Auckland,New Zea-land,2016:1-7.
[3] 陈鹏飞,王彦伟.基于ModelCenter的精密气浮工件台系统建模与参数优化 [J].组合机床与自动化加工技术,2014(4):26-29.
(CHEN Peng-fei,WANG Yan-wei.System modeling and parameters optimization of ultra-precision stage based on ModelCenter [J].Modular Machine Tool & Automatic Manufacturing Technique,2014(4):26-29.)
[4] Kamaldin N,Chen S L,Kong C J,et al.Adaptive parameter and gain RISE control of a flexure-based dual-drive ‘H’ gantry [C]//IEEE International Conference on Advanced Intelligent Mechatronics.Alberta,Canada,2016:1240-1245.
[5] Lin C J,Lee C Y.Observer-based robust controller design and realization of a gantry stage [J].Mechatronics,2011,21(1):185-203.
[6] Dashi D.Modeling,analysing dynamics and designing controllers of an H-drive [R].Netherlands:University of Twente,2006.
[7] Zhao Y,Yang K,Zhu Y,et al.Modeling and analyzing of an H-drive precision XY stage [C]//Mechanic Automation and Control Engineering (MACE).Wuhan,China,2010:6311-6314.
[8] Lin F Z,Hsieh H J,Chou P H,et al.Digital signal processor-based cross-coupled synchronous control of dual linear motors via functional link radial basis function network [J].The Institution of Engineering and Technology IET Control Theory and Applications,2011,5(4):552-564.
[9] Lin F Z,Chou P H,Chen C S.DSP-based synchronous control of dual linear motors via sugeno type fuzzy neural network compensator [C]//Electrical Machines and Systems (ICEMS).Beijing,China,2011:1-6.
[10]刘强,张从鹏.直线电机驱动的H型气浮导轨运动平台 [J].光学精密工程,2007,15(10):1540-1546.
(LIU Qiang,ZHANG Cong-peng.H type air bearing the vibmotion stage driven by linear motors [J].Optics and Precision Engineering,2007,15(10):1540-1546.)
[11]李静,何永义,方明伦,等.曲轴非圆磨削中基于差分进化算法的变参数交叉耦合轮廓控制 [J].机械工程学报,2011,47(9):139-145.
(LI Jing,HE Yong-yi,FANG Ming-lun,et al.Cross-coupled contour control with variable parameters based on differential evolution algorithm in rankshaft non-circular grinding [J].Journal of Mechanical Engineering,2011,47(9):139-145.)
[12]董伯麟,刘洋,王治森.基于双NURBS参数混合插补算法的五轴联动交叉耦合控制器研究 [J].中国机械工程,2014,25(22):3038-3044.
(DONG Bo-lin,LIU Yang,WANG Zhi-sen.Study on 5-Axis CNC system cross-coupled controller based on double NURBS hybrid parametric interpolation algorithm [J].China Mechanical Engineering,2014,25(22):3038-3044.)
[13]Chung S J,Slotine J J E.Cooperative robot control and concurrent synchronization of Lagrangian systems [J].IEEE Transactions on Robotics,2009:25(3):686-700.
Cross-coupledfuzzyPIDsynchronouscontrolforH-typeprecisionmotionplatform
WANG Li-mei, ZHANG Zong-xue
(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)
Aiming at the nonsynchronous movement problem of both sides of H-type precision motion platform driven by two permanent magnet linear synchronous motors (PMLSM) which is caused by such uncertain factors as motor parameter variation and disturbance of PMLSM, an cross-coupled fuzzy PID control method was proposed.In the single axis, the fuzzy PID control was taken as the position controller, and the ordinary PI control was taken as the speed controller to guarantee the tracking accuracy of signal axis.In addition, the cross-coupled control (CCC) method was introduced into the two axes to eliminate the mechanical coupling between the two PMLSM, so that the synchronous position error between the two axes could be reduced.The results show that the control method combined the cross-coupled and fuzzy PID control can make the synchronous error of H-type precision motion platform converge to zero, and can make the system have good tracking performance and robustness.
H-type precision motion platfrom; cross-coupled control; fuzzy PID control; synchronous error; permanent magnet linear synchronous motor (PMLSM); tracking accuracy; synchronous motion; mechanical coupling
2016-11-01.
国家自然科学基金资助项目(51175349);辽宁省自然科学基金资助项目(2015020151).
王丽梅(1969-),女,辽宁建平人,教授,博士生导师,主要从事交流伺服驱动技术等方面的研究.
* 本文已于2017-10-25 21∶13在中国知网优先数字出版.网络出版地址:http://kns.cnki.net/kcms/detail/21.1189.T.20171025.2113.056.html
10.7688/j.issn.1000-1646.2018.01.01
TM 359.4
A
1000-1646(2018)01-0001-05
景 勇 英文审校:尹淑英)

