大椭圆轨道挠性卫星姿态快速机动控制研究
张 洋,朱 野,李 东,鹿 艺,朱振才
(中科院 微小卫星创新研究院,上海 201103)
大椭圆轨道挠性卫星姿态快速机动控制研究
张 洋,朱 野,李 东,鹿 艺,朱振才
(中科院 微小卫星创新研究院,上海 201103)
对具挠性附件的大椭圆轨道卫星快速姿态机动控制进行了研究。针对此类卫星的非线性姿态动力学特点,用非线性矩阵二阶系统形式建立了卫星刚体与柔性结构模态耦合的动力学模型,用反馈非线性化将其转换为一类多胞线性参变系统。针对该系统设计线性状态反馈控制律实现区域极点配置,将相应控制律参数的求解转换为线性矩阵不等式约束下的凸优化问题。仿真结果表明:所提控制方法可同时实现挠性卫星的快速机动控制和挠性振动的有效抑制,能满足大椭圆轨道运行的挠性卫星完成不同观测区域切换的姿态控制任务。研究为大椭圆轨道挠性卫星的小角度快速机动控制提供了理论支撑。
大椭圆轨道; 挠性卫星; 快速姿态机动; 刚柔耦合; 反馈非线性; 多胞线性参变系统; 凸优化; 挠性振动抑制
0 引言
大椭圆轨道(HEO)也称为Molniya轨道,因前苏联的Molniya通信卫星系统首次使用而得名。该轨道的远地点约40 000 km,近地点约500~2 000 km,形成一个偏心率约0.741的椭圆轨道。轨道倾角近63°,轨道周期约705.928 min(11 h 46 min,近似称作12 h轨道)。这种轨道允许卫星长时间停留在北半球上空,观察在GEO卫星轨道上无法观察到的北极地区。大椭圆轨道卫星可通过姿态机动方式观测不同的任务区域,观测区域切换也对卫星平台的快速机动性能提出了较高要求,同时对定向精度和对地成像的稳定度均相应提出较高要求。但其携带的太阳帆板等挠性附件的结构模态阻尼较小,在卫星快速姿态机动过程中可能会激发挠性附件的振动,这会直接影响卫星的姿态稳定度[1]。因此,卫星姿态控制系统分析和设计时须考虑挠性附件变形和振动的影响。
近年来,矩阵二阶系统作为控制系统的一个主要研究方向,在机器人、空间飞行器和机械结构振动等领域得到了广泛应用[2-7]。用矩阵二阶形式描述对象的优点是:保留了原系统的物理特性;对象维数低于采用矩阵一阶形式描述的模型,提高了计算效率;保留了原矩阵的稀疏性和其他特殊性质,便于分析与设计;可直接利用原系统的加速度状态设计反馈控制律。因此,用矩阵二阶形式描述的系统更适于构建实际系统,但目前关于控制系统设计的相关研究主要集中于稳定性分析、极点配置、特征结构配置、部分极点配置和观测器设计等[2-12]。其中:文献[2]分析了以矩阵二阶形式描述的线性定常系统的渐近稳定性和 Lyapunov 稳定性, 并给出了该系统渐近稳定的充要条件;文献[4]针对一类矩阵二阶系统, 提出了一种求解多输入系统部分极点配置问题的新算法;文献[8,12]针对线性矩阵二阶系统采用 PD 反馈控制实现了特征结构配置,并给出了参数化求解方法,以及二阶Sylvester 矩阵方程的求解方法及其在特征结构配置设计中的应用。文献[7]给出了在矩阵二阶系统框架下设计观测器增益的条件。上述研究多基于线性矩阵二阶系统的框架,针对非线性矩阵二阶系统的研究较少。
本文对有挠性附件的大椭圆轨道挠性卫星姿态快速机动控制进行了研究。针对大椭圆轨道挠性卫星的非线性姿态动力学特点,用非线性矩阵二阶系统描述挠性卫星姿态动力学模型,由非线性反馈化法将其转为一类多胞线性参变系统,针对该系统设计线性状态反馈控制律,给出了控制器参数的优化求解策略,并通过数值仿真验证了所提非线性反馈控制方法实现挠性卫星快速机动控制和挠性振动抑制的有效性。
1 挠性卫星动力学建模
精确的姿态控制律须建立在实际有效的动力学模型基础上,应根据具挠性附件的卫星特点建立卫星刚体与柔性结构模态耦合的动力学模型。建立混合坐标中挠性卫星姿态动力学基本方程为
(1)
式中:J为整星转动惯量矩阵;ω为卫星姿态角速度;p为帆板的耦合系数向量;η为挠性模态坐标向量;C=2diag[ζ1·ω1ζ2·ω2…ζn·ωn];Ξ为挠性阻尼系数矩阵;Ω为挠性模态频率矩阵;K=diag[(ω1)2(ω2)2… (ωn)2];T为挠性卫星控制力矩[13]。此处:
J=diag[JxJyJz]
ω=[φθψ]T
p=[p1p2…pn]T
η=[η1η2…ηn]T
Ξ=diag[ζ1ζ2…ζn]
Ω=diag[ω1ω2…ωn]
T=[TxTyTz]T
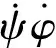
(2)
(3)
定义非线性矩阵二阶系统模型中各分块矩阵分别为
M11=diag[Jx-pTpJyJz]
M12=03×n
M21=0n×3
M22=(Jx-pTp)In
C12=[-pTC00]T
C21=[00(Jy-Jz)pγ]
C22=ppTC+(Jx-pTp)C
K11=03×3
K12=[-pTK00]T
K21=0n×3
K22=ppTK+(Jx-pTp)K
τ1=[TxTyTz]T
τ2=pTx
即非线性矩阵二阶系统模型中,C11,C21含时变参数γ。
2 挠性卫星非线性动力学模型的反馈线性化
为便于叙述,定义线性参变系统和多胞线性参变系统如下[14]。
定义1线性参变系统。线性参变系统状态向量为x,系统输出向量为y,系统输入向量为u,则状态空间可描述为
(4)
式中:A(υ),B(υ),C(υ),D(υ)为时变参数向量υ=υ(t)的仿射线性函数。
定义2多胞线性参变系统。当系统式(4)为线性参变系统,且满足υ取值于某一给定的多胞域内,即
υ∈Co{υp1υp2…υpn}
(5)
式中:{υp1υp2…υpn}为由该多胞域的顶点组成的集合。则称系统式(4)为多胞线性参变系统。
由上,用矩阵二阶系统形式描述的挠性卫星非线性动力学模型式(3)的反馈线性化过程可表述为以下定理。
定理1非线性系统式(3),若满足以下假设条件:
M11,M22均为可逆常值矩阵。
M11-M12(M22)-1M21,M22-M21(M11)-1M12均非奇异。
另外,控制输入τ具形式
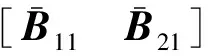
(6)

证明:由式(3)可知
γ[00(Jy-Jz)p0|0]
(7)
式中:
o1=ppTK+(Jx-pTp)K
o2=ppTC+(Jx-pTp)C
因M11,M22为可逆常值矩阵,则(W1)-1=M11-M12(M22)-1M21,(W2)-1=(M22-M21(M11)-1×M12)-1均为可逆常值矩阵。定义状态变量
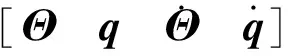
(8)
式中:
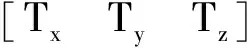
A11=-W1(K11-M12(M22)-1K21)
A12=-W1(K12-M12(M22)-1K22)
A13(γ)=-W1(C11-M12(M22)-1C21)
A14=-W1(C12-M12(M22)-1C22)
A21=-W2(K21-M21(M11)-1K11)
A22=-W2(K22-M21(M11)-1K12)
A23(γ)=-W2(C21-M21(M11)-1C11)
A24=-W2(C22-M21(M11)-1C12)
将C11,C21代入,可得A(γ)=A0+γA1。由定义2可知:系统式(10)是以u为控制输入的多胞线性参变系统。定理得证。
3 反馈控制律设计

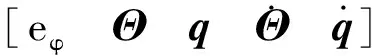
(9)
式中:u为控制量,且u=[TxTyTz]T;K为反馈控制增益矩阵。增广线性参变闭环控制系统如图1所示。
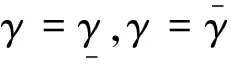
(N(BT))T[(A(γ))TX+XA(γ)+2σX]N(BT)<
0
(10)
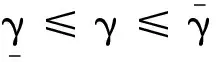
为避免直接求解被控对象含γ的控制器K,可利用多胞线性参变系统的凸特性求解。
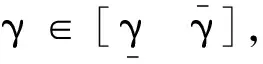
0
(11)
0
(12)
为避免在求解Q的过程中出现条件数过大的Q,可附加约束
I2N+7 (13) 则可将LMIs求解问题转为标准凸优化问题 (14) 设挠性卫星的主转动惯量为 [6 500 5 000 4 500] kg·m2 太阳帆板前2阶模态挠性参数见表1。 表1 太阳帆板前2阶挠性参数 其中:k11=-381.1,k12=-0.7,k13=0,k14=0.1,k15=-217,k16=-273.8,k17=-1 676,k18=0,k19=0.1,k110=-252.1,k111=-184.4;k21=0.001,k22=-0.001,k23=-8 100,k24=0,k25=0,k26=0,k27=0,k28=-6 633,k29=0,k210=0,k211=0;k31=-8.1,k32=0.536 4,k33=0,k34=-5 672,k35=-5.7,k36=-15,k37=-30.5,k38=0,k39=-4 643,k310=-3.6,k311=-1.1。用控制律式(11)对被控对象进行闭环控制,仿真所得挠性卫星姿态角及其速率变化分别如图2、3所示,挠性模态振动抑制响应如图4所示。 由图4可知:因太阳帆板与卫星平台的耦合作用,挠性卫星滚动轴机动过程中相应诱发了太阳帆板的挠性振动,但随着控制力矩持续作用,前2阶挠性模态的振动幅值均迅速衰减。因此,本文考虑挠性模态设计的控制律能保证闭环系统的稳定性。 仿真所得挠性卫星滚动轴机动至目标位置过程的三轴控制力矩输出如图5所示。因滚动轴在15 s内完成快速小角度机动,同时需抑制可能激发的太阳帆板挠性振动,故滚动轴输出的控制力矩最大达0.64 N·m,俯仰轴的控制力矩主要控制时变参数的变化,偏航轴的控制力矩用于抵消姿态耦合作用。在三轴控制力矩共同作用下,挠性卫星同时实现了姿态角的渐近跟踪和挠性结构的振动抑制。 针对在大椭圆轨道上运行有挠性附件的卫星在切换观测区域任务过程中的非线性动力学特点,本文对卫星的姿态快速机动控制进行了研究。建立以非线性矩阵二阶系统形式描述挠性卫星姿态动力学模型,用反馈线性化法将其转为一类多胞线性参变系统,针对该系统设计线性状态反馈控制律实现区域极点配置,并将该控制律参数的求解转为线性矩阵不等式约束下的凸优化问题。数值仿真挠性卫星在切换观测区域过程中滚动轴姿态机动至目标位置的控制过程结果表明:本文提出的控制方法可同时实现挠性卫星的快速机动控制和挠性振动的有效抑制,能满足大椭圆轨道运行的挠性卫星完成不同观测区域切换的姿态控制任务。本文提出的方法主要适于卫星姿态小角度快速机动的任务要求。后续将在此基础上,进一步研究卫星姿态大角度快速机动和三轴姿态机动的控制方法,以适应卫星多种任务的应用需求。 [1] 程磊, 王天舒, 李俊峰. 挠性多体卫星姿态动力学与控制[J]. 清华大学学报(自然科学版), 2005, 45(11): 1506-1509. [2] DIWEKAR A M, YEDAVALLI R K. Stability of matrix second order systems: new conditions and perspectives[J]. IEEE Trans on Automatic Control, 1999, 144(9): 173-1177. [3] FUJISAKI Y, IKEDA M, MIKI K. Robust stabilization of large structures via displacement feedback[J]. IEEE Trans on Automatic Control, 2001, 46(12): 1993-1996. [4] DATTA B N, SARKISSIAN D. Multi-input partial eigenvalue assignment for a symmetric quadratic pencil[C]// Proc of American Control Conference. San Diego: [s. n.], 1999: 2244-2247. [5] DUAN G R. Parametric eigenstructure assignment in second order descriptor linear systems[J]. IEEE Trans on Automatic Control, 2004, 49(10): 1789-1794. [6] DATTA B N, LIN W W, WANG J N. Robust and minimum gain partial pole assignment in vibration structures with aerodynamics effects[C]// Proc IEEE Conf Decision Control. Piscataway: IEEE, 2003: 2358-2363. [7] KWAK S K, YEDAVALLI R K. Observer designs in matrix second order system framework: measurement conditions and perspectives[C]// Proc of the American Control Conference. Chicago: [s. n.], 2000: 2316-2320. [8] 顾大可, 臧金鑫, 段广仁. 利用位置和加速度反馈的矩阵二阶系统特征结构配置[J]. 信息与控制, 2016, 45(3): 301-305. [9] 陈武华, 薛飞飞, 刘利军. 二阶Lipschitz非线性系统自然观测器设计[J]. 广西大学学报(自然科学版), 2015, 40(6): 1406-1413. [10] 王品, 姚佩阳. 具有不同输入时延的二阶多智能体系统一致性[J]. 复杂系统与复杂性科学, 2016, 13(4): 102-107. [11] 安博林. 基于一类二阶线性变参系统特征结构配置的完全参数化方法[J]. 化工自动化及仪表, 2016(5): 457-461. [12] 顾大可, 段广仁. 矩阵二阶线性系统的鲁棒渐近跟踪[J]. 信息与控制, 2013, 42(2): 181-188. [13] 张洋. 挠性卫星小角度快速机动及稳定控制[J]. 光学精密工程, 2012, 12(S1): 166-171. [14] APKARIAN P, GAH INET P, BECKER G. Self-scheduledH∞control of linear parameter-varying systems: a design example[J]. Automatica, 1995, 31(9): 1251-1261. [15] 王永, 张洋, 张国庆. 一类非线性矩阵二阶系统的反馈LPV化控制[J]. 中国科学技术大学学报, 2008, 38(7): 815-820. StudyonFastAttitudeManeuverControlofFlexibleSatellitewithLargeEllipticalOrbit ZHANG Yang, ZHU Ye, LI Dong, LU Yi, ZHU Zhen-cai (Innovation Academy for Microsatelltes, Chinese Academy of Sciences, Shanghai 201103, China) The high-precision control of a satellite with flexible appendage in the large elliptical orbit to achieve rapid attitude maneuver was studied in this paper. According to the dynamic characteristics of nonlinear attitude of these satellites, the dynamic model with the coupling of the rigid body and flexible structure was established by the nonlinear matrix second order system form. The model was transformed into a polytopic linear parameter varying system. Then linear state feedback control law was designed to realize the regional pole assignment of the system according to the linear parameter varying system. So the solving problem of the control law parameters was transformed into a convex optimization problem with linear matrix inequalities constraints. The simulation results showed that the fast maneuvering control and flexible suppress of the flexible satellite could be realized at the same time by using the method proposed, which could realize the switching different observation area mission of flexible satellite in large elliptical orbit. The study has provided a theoretical support for small maneuvering angle fast switching observation mission of flexible satellite in large elliptical orbit. large elliptical orbit; flexible satellite; fast attitude maneuver; rigid and flexible coupling; nonlinear feedback; polytopic linear parametric system; convex optimization; flexible vibration suppress 2017-10-31; 2017-11-18 国家自然科学基金资助(41504057) 张 洋(1983—),男,博士,主要研究方向为卫星总体设计。 1006-1630(2017)06-0020-06 V448.2 A 10.19328/j.cnki.1006-1630.2017.06.0044 数值仿真



5 结束语

