挠性接管布置对管路系统振动特性的影响分析
戴青山,张振海,刘树勇
(1. 海军工程大学 动力工程学院,湖北 武汉 430033;2. 船舶振动噪声重点实验室,湖北 武汉 430033)
0 引 言
船舶内部管路布置数量众多且系统复杂,管路系统振动噪声成为影响船舶振动噪声性能的重要因素。因此,对船舶管路系统采取有效的减振降噪措施十分必要[1]。目前,挠性接管技术是有效抑制管路系统振动噪声的方法之一。国外已在船舶上大量使用挠性接管,并修订了详细的相关标准,对船用挠性接管的设计、检验、安装及维护保养等方面进行了详细说明[2]。挠性接管是一种带横向波纹的圆柱形薄壁弹性壳体,在管路和设备中起着吸振、密封、热补偿等作用[3],其主要由橡胶体和金属连接件组成,其中橡胶体一般由内层胶、增强层和外层胶经硫化或扣压成型[4–5]。挠性接管不但能阻隔和衰减管系的结构振动噪声,还能抑制流致振动噪声[6–7]。很多文献认为:挠性胶管离振源越近,其共振的剧烈程度有所减轻,并且发生共振的频率向低频方向移动,总的来说,挠性接管布置得离振源近一些对控制弯曲波沿管路的传递有利。在一般情况下,在水泵进、出口加装挠性接管可以有效控制水泵传递到管路系统的振动,但实际安装过程中,由于受船舶上安装空间限制因素影响,其出口处往往没有位置安装挠性接管,那么此时往往会将水泵出口与弯管直接相连,而将挠性接管安装在弯管后面,便于挠性接管的低噪声安装。
相关专家和学者对挠性接管进行了研究。熊永华等[8]基于有限元理论建立了金属波纹管模型,并在单点激励载荷作用下计算了波纹管在时、频域内的瞬态动力学响应。最后通过试验验证了仿真计算的可靠性和准确性,但波纹管位置因素对管系振动特性影响待臻完善。美国研究人员针对管路挠性连接件结构声传递损失进行了系统研究,结果表明:管内介质和管体的长度、壁厚及管径等因素均对挠性接管结构振动传递损失有不同程度的影响[9]。尽管其对挠性接管参数进行了研究,但缺乏挠性接管低噪声安装位置参数的补充。赵应龙[10]对橡胶挠性接管的静、动态特性进行了理论研究,对本文研究挠性接管振动特性理论分析有一定的指导意义。王小锋[11]研制出了一款新型处于压缩状态的挠性接管,其隔振效果良好,但文献中并没有确立挠性接管在管系中的安装参数。目前,多数有关挠性接管的文献都没有深入研究挠性接管安装位置影响,因此有必要针对挠性接管安装位置对管系振动特性影响的问题展开深入研究[12]。
本文仿真分析了管系挠性接管安装于弯管前端、后端时管系的振动特性,并通过实验验证了仿真结果的正确性。选择合适的安装位置不仅可以达到减振降噪目的,还能更加方便地对挠性接管进行更换从而减少安装时间以提升系统的可靠性。本文的研究工作为挠性接管的低噪声安装提供了实践参考和理论依据。
1 数学模型的建立
1.1 挠性接管动力学模型
橡胶挠性接管的简化动力学模型如图1所示,中间部分是橡胶材料的等效动力学模型。
根据有限元理论和振动理论,挠性接管多自由度弹性系统的动力学方程为[13–14]


图 1 简化力学模型Fig. 1 Simplified mechanical model
式中:,,分别为结构的质量矩阵,阻尼矩阵,刚度矩阵;,,分别为结构的加速度响应,速度响应和位移响应;为结构的激振力向量。
如果为激振力的力幅,则、、在经过较短时间之后,将变为稳定的周期性简谐振动响应。如果激振力换成复数力即那么位移、速度、加速度也将具有复数形式:

其中,也是复数量,称为复数位移矢量。将式(2)代入式(1)时,可以根据模态理论求得该系统的固有频率矩阵和固有振型矩阵。在模态坐标中,用振型矩阵作为坐标系统空间的基向量矩阵,即,为模态坐标向量,则可将式(1)变换为

其中,为频响函数矩阵。因此在知道了外部激励的情况下,就可以根据式(3)计算出系统对于该激励的响应,同样,在知道了和时,也可以计算出频响函数。
1.2 典型管路系统振动噪声特性计算分析
管路系统由许多管段、元件和支撑组成。如果不考虑各运动之间的相互作用,振动沿管路系统的传递可以由每一方向各管段、元件和支撑的传递组合而成。如果元件均为串联连接,总的传递矩阵是各传递矩阵的乘积,如下式:

式中:为单元总数;为第i个单元的传递矩阵。
只要确定每一个元件的传递矩阵,则可获得整个系统的振动传递特性。实际上,大多数管路元件不能直接得到传递矩阵,要通过阻抗矩阵转换获得。阻抗矩阵可以通过测量获得。管系中的某些元件可以看作简单力学单元,它们的传递矩阵较为简单。质量为M的纯质量元件的传递矩阵如下式:i

刚度为的弹簧的传递矩阵如下式:

阻尼系数为的粘性阻尼器的传递矩阵如下式:
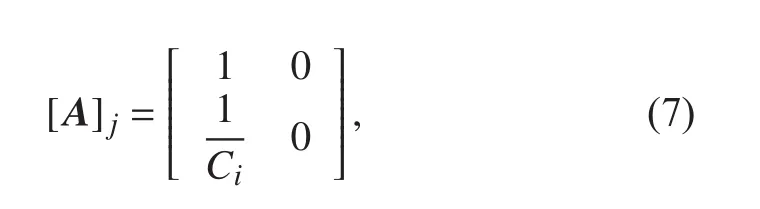
无阻尼的质量——弹簧振子的四端参数矩阵为质量和弹簧传递矩阵的乘积,其传递矩阵如下式:
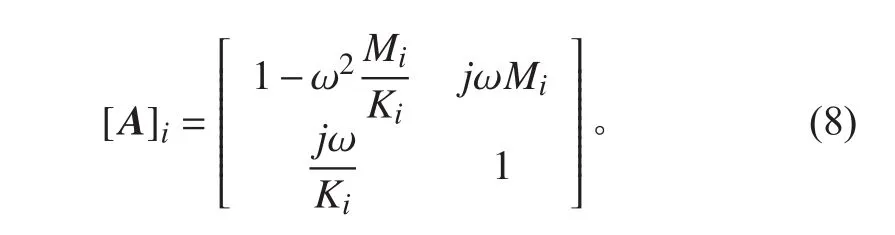
以上传递矩阵都是理想边界条件,即完全刚性或完全自由边界条件下得到的。已知传递特性的元件在有限阻抗边界的情况下,传递特性相应地随之改变。

图 2 传递特性分析Fig. 2 Transmission characteristics analysis
输出端的输入阻抗如下式:

根据传递矩阵的代数方程组,输入端的输入阻抗如下式:

传递阻抗如下式:

力传递率如下式:

运动传递率如下式:

带有限阻抗边界的元件前、后的振级落差可表示为下式:

在低于共振频率的低频时,一般,则有

由于很难直接测量挠性接管的传递矩阵,于是通过实验测得管路系统中的挠性接管的阻抗矩阵再通过传递矩阵和阻抗矩阵之间的转换关系,获得挠性接管的相应传递矩阵。转换关系如下式:
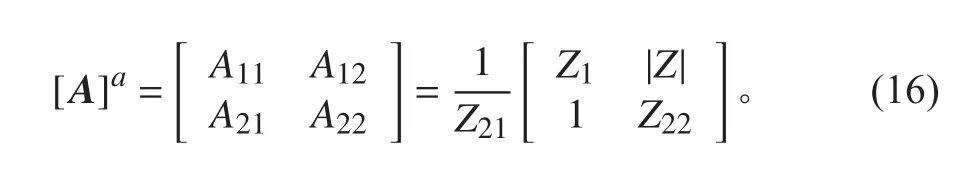
2 有限元建模
管系仿真模型主体为中间安插着附有橡胶属性挠性接管的一段弯管,其两端处于固定状态,其余管路主体部分均处于自由状态。通过改变挠性接管在弯管前后的安装位置,计算了在2种不同挠性接管安装位置时指定点的振动响应。
2.1 管路系统参数
DN80管路参数如表1所示,管路弹性支撑有限元模型的材料属性如表2所示。

表 2 模型材料属性Tab. 2 Model material data
2.2 基于Abaqus的管路系统挠性接管安装有限元模型
在有限元软件中建立挠性接管安装在不同位置时的管路系统有限元模型:在三维图形软件UG8.0中建立待分析的直弯管模型,并导入Abaqus的Part模块中创建所需分析的实体结构模型,考虑到挠性接管的复杂性可以把其简化为实体橡胶属性单元结构。选择适当的本构关系,定义模型的材料属性和截面,并确立管路以及挠性接管的相关参数。将管路两端设为固支,在管路的左端管口附近设置沿Y轴向下的单位激励力。管路系统的Abaqus模型如图3所示。

图 3 安装挠性接管管系有限元模型Fig. 3 Finite element model of flexible pipe installed in the pipeline system
3 仿真结果分析

图 4 响应点的振动加速度Fig. 4 Vibration acceleration of respond point
对挠性接管安装于管路系统弯管前端和后端时的振动响应进行仿真计算,得到响应点的振动响应频谱如图4所示。由图4可知,在0~400 Hz以及650~800 Hz频段内挠性接管安装在弯管后端的振动加速级要比安装在前端时稍高一些,而在800~1 000 Hz的频段内安装在后端时该点的振动响应要比安装在前端时稍低一些。根据该点的振动传递特性,可初步得出结论:管系振动传递特性并没有随挠性接管安装于弯管前、后端位置的不同,而存在较大差异。
4 实验验证
本文以中船重工702所管路振动噪声实验室中由泵驱动的DN80回路为实验台架,实验管路系统的分布情况如图5所示。
挠性接管安装在弯管前端如图6所示,挠性接管安装在弯管后端如图7所示,测试管路系统响应点的振动传递特性,并对比2种安装方式对管路系统及船体振动的影响。

图 5 挠性接管安装位置示意图Fig. 5 Location diagram of the installed flexible pipe

图 6 挠性接管安装于弯管前端Fig. 6 Flexible pipe installed in the front of the bend

图 7 挠性接管安装于弯管后端Fig. 7 Flexible pipe installed in the back of the bend
选取图5中所示的1号(图中的1#)法兰和9号(图中的9#)法兰分析挠性接管与弯管相对位置变化前后管路系统的振动情况。
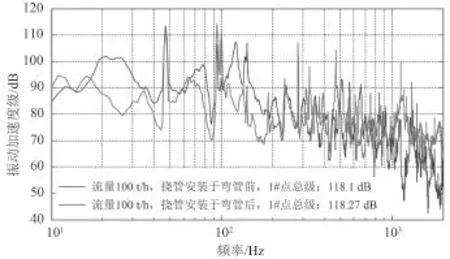
图 8 1号法兰振动加速度Fig. 8 Vibration acceleration of number 1 flange

图 9 9号法兰振动加速度Fig. 9 Vibration acceleration of number 9 flange
由图8和图9所示的测试结果可知,2种工况相同测点振动加速度总级相差很小,说明无论是挠性接管与水泵出口直接相连(即安装在弯管前端)或是连接在水泵出口的弯管后端,对管路系统测点的振动加速度级影响较小。
5 结 语
通过对挠性接管不同安装位置下弯管系统振动特性的仿真分析和台架试验,得出如下结论:
1)采用同一种橡胶挠性接管,在管路上不同位置安装,会使隔振效果发生微小变化,靠近振源进出口处安装要优于远离的效果;在管路设置挠性接管的控制要求如下:
① 挠性接管的布置应尽量靠近振动源;
② 船舶上实际安装过程中,若安装空间不允许,可根据空间位置适当调整挠性接管与振动源的相对位置,但应该尽量靠近振动源。
2)挠性接管结构较为复杂,由于有限元计算软件方面的局限性,利用有限元建立挠性接管建模仿真,很难模拟出挠性接管的强度、刚度以及插入损失等一些实际参数,因此模拟仿真和实际响应结果还存在较大的差异。深入研究挠性接管的接入状况,建立合理的挠性接管的有限元计算模型,并通过试验验证提出合理的设计方法是今后挠性接管研究的又一重要课题。
3)尽管以上研究证明:挠性接管安装在管系弯管前或后端对其的振动传递特性的影响并不是很大,但是研究还存在着很多影响因素,比如:挠性接管本身性能参数与系统不匹配等,还有待进一步研究。
[1] 王艳林, 王自东, 宋卓斐, 等. 潜艇管路系统振动噪声控制技术的现状与发展[J]. 舰船科学技术, 2008, 30(6): 34-38.WANG Yan-lin, WANG Zi-dong, SONG Zhuo-fei, et al.Present situation and development of vibration and noise control technology for submarine pipeline system[J]. Ship Science and Technology, 2008, 30(6): 34-38.
[2] Naval Engineering Standard. Ministry of Defence. U. K.Requirements for Flexible Rubber Pipe Assemblies and Bellows for Use in Systems from Vacuum to 10 bar[S]. 2000.
[3] MUNJA M L, THAWAN P T. I prediction of the vibroacoustic transmission loss of planarhose-pipe systems[J].Journal Acoustical Society of America. 1997, 101.
[4] SHUAI Chang-geng, HE Lin, LV Zhi-qiang.The development of studying flexible pipe bend reinforced by kevlar fibers[J].Journal of Marine Science and Application. 2003, 2(2): 61-66.
[5] 朱石坚, 何琳. 船舶减振降噪技术与工程设计[M]. 北京:科学出版社, 2002.
[6] APIRP B. Recommended practice for flexible pipes[M].Washington: American Petroleum Institute. 1998.
[7] BROWN P A. A theoretical approach to prediction of service life of unbonded flexible pipes under dynamic loading conditions[J]. Marine Structures 1992.19(5): 399-429.
[8] 熊永华, 杜发荣, 钟玉平. 金属波纹管的动态特性分析与振动试验研究[J]. 中国机械工程2008, 19(10): 1177-1180.XIONG Yong-hua, DU Fa-rong, ZHONG Yu-ping. Study on dynamic characteristics and vibration test of metal bellows[J].China Mechanical Engineering 2008, 19(10): 1177-1180.
[9] 柴小文. 舰用挠性接管技术现状和进展[J]. 振动与噪声控制,2007, 10(5): 13-16.CHAI Xiao-wen. Current situation and development of flexible pipe joint for ship[J]. Vibration and Noise Control, 2007,10(5): 13-16.
[10] 赵应龙, 何琳. 橡胶挠性接管特性研究[J]. 海军工程大学学报, 2001, 13(1): 61-64.ZHAO Ying-long, HE Lin. Study on the characteristics of flexible rubber pipe joint[J]. Journal of Naval University of Engineering, 2001, 13(1): 61-64.
[11] 王小锋, 周勇, 刘春林, 等. 新型压缩式橡胶挠性接管结构设计与试验[J]. 振动与噪声控制, 2013, 33(6): 207-211.WANG Xiao-feng, ZHOU Yong, LIU Chun-lin, et al.Structural design and test of a new type flexible rubber flexible pipe[J]. Vibration and Noise Control, 2013, 33(6): 207-211.
[12] 蔡亦钢. 流体传输管道动力学[M]. 杭州: 浙江大学出版社,1990.
[13] 李德葆, 陆秋海. 工程振动试验分析[M]. 北京: 清华大学出版社, 2004.
[14] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.

